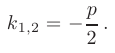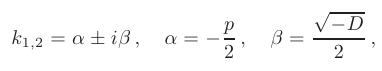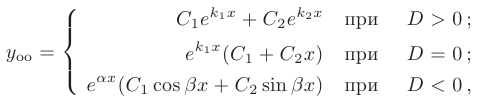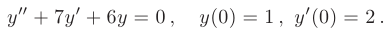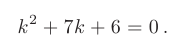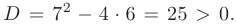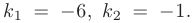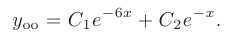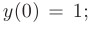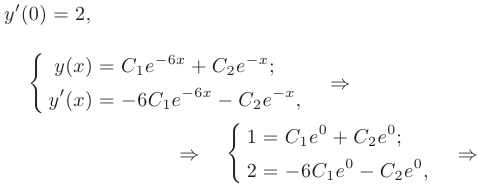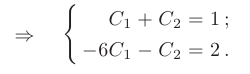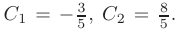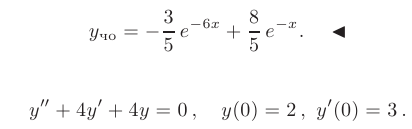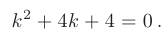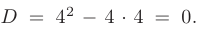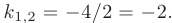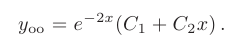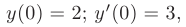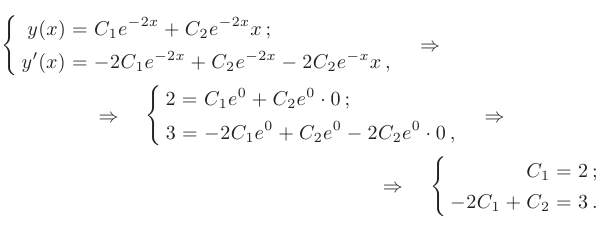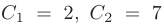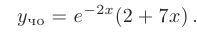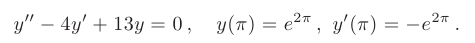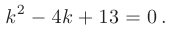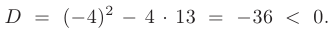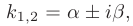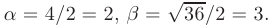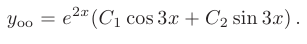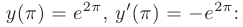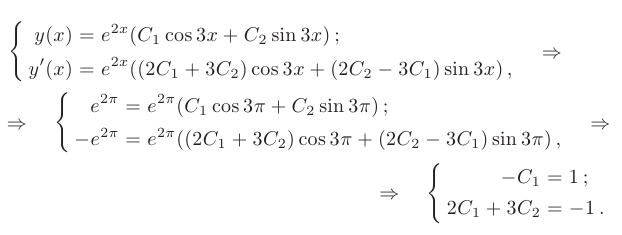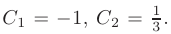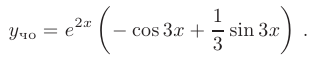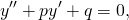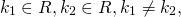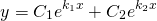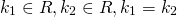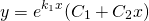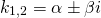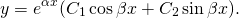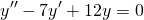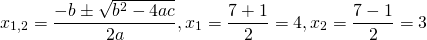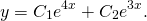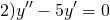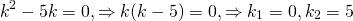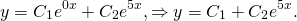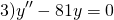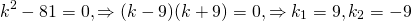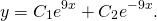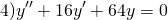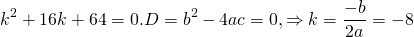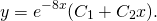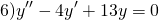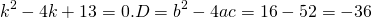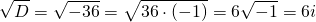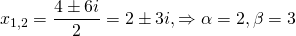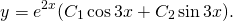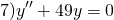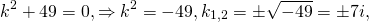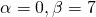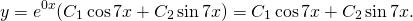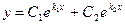Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами в математике
Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами
Рассмотрим метод решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами:
Линейной комбинацией функций 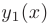
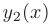
где 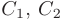
Функции 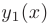
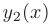
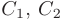
Теорема 7.2. Если 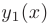
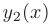
Следовательно, чтобы найти общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, надо знать два его частных линейно независимых решения: 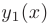
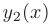
Будем искать частное решение дифференциального уравнения в виде 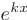
Очевидно, функция 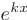
которое называется характеристическиль уравнением исходного дифференциального уравнения.
Как известно, для корней данного квадратного трехчлена возможны три случая.
- Если дискриминант больше нуля
, то корни характеристического уравнения действительные, простые:
- Если дискриминант равен нулю (
= 0), то корни характеристического уравнения действительные, кратные:
- Если дискриминант меньше нуля (
где 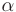
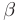
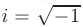
Теорема 7.3. Общее решение 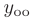
где 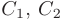
Пример:
Найти частные решения заданных линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами, удовлетворяющие начальным условиям:
► Составим характеристическое уравнение, заменяя в дифференциальном уравнении производные неизвестной функции у соответствующими степенями неизвестного 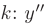
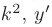
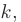
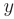
Дискриминант уравнения больше нуля:
В таком случае, корни характеристического уравнения действительные, простые:
Следовательно, общее решение дифференциального уравнения имеет вид
Частное решение получим из общего, используя для определения произвольных постоянных заданные начальные условия:
Решая полученную систему, находим значения произвольных постоянных:
После подстановки найденных значений в общее решение, искомое частное решение принимает вид
► Составим характеристическое уравнение:
Дискриминант уравнения равен нулю:
В таком случае, корни характеристического уравнения действительные, кратные:
Следовательно, общее решение дифференциального уравнения имеет вид
Найдем производную общего решения и определим произвольные постоянные из начальных условий:
Находим значения произвольных постоянных:
и подставим их в общее решение. Искомое частное решение принимает вид
Составим характеристическое уравнение:
Дискриминант меньше нуля:
В таком случае, корни характеристического уравнения комплексно-сопряженные:
Следовательно, общее решение дифференциального уравнения имеет вид
Используем для определения произвольных постоянных заданные начальные условия:
После подстановки найденных значений в общее решение, получим:
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами имеют вид
где p и q — действительные числа. Рассмотрим на примерах, как решаются однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Решение линейного однородного однородного дифференциального уравнения второго порядка зависит от корней характеристического уравнения. Характеристическое уравнение — это уравнение k²+pk+q=0.
1) Если корни характеристического уравнения — различные действительные числа:
то общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид
2) Если корни характеристического уравнения — равные действительные числа
(например, при дискриминанте, равном нулю), то общее решение однородного дифференциального уравнения второго порядка есть
3) Если корни характеристического уравнения — комплексные числа
(например, при дискриминанте, равном отрицательному числу), то общее решение однородного дифференциального уравнения второго порядка записывается в виде
Примеры решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
Найти общие решения однородных дифференциальных уравнений второго порядка:
Составляем характеристическое уравнение: k²-7k+12=0. Его дискриминант D=b²-4ac=1>0, поэтому корни — различные действительные числа.
Отсюда, общее решение этого однородного ДУ 2-го порядка есть
Составим и решим характеристическое уравнение:
Корни действительные и различные. Отсюда имеем общее решение данного однородного дифференциального уравнения:
В этом случае характеристическое уравнение
Корни различны и действительны. Поэтому общее решение однородного дифференциального уравнения 2-го порядка здесь
Поскольку корни действительны и равны, для этого дифференциального уравнения общее решение записываем как
Характеристическое уравнение здесь
Так как дискриминант — отрицательное число, корни характеристического уравнения — комплексные числа.
Общее решение этого однородного дифференциального уравнения второго порядка имеет вид
Отсюда находим общее решение данного диф. уравнения:
Примеры для самопроверки.
Найти общее решение однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение
Для того, чтобы решить это уравнение надо составить характеристическое уравнение, которое получается из данного уравнения , если в нем заменить y»=k 2 , y’=k, a y=k 0 =1.
— это квадратное уравнение.
Общее решение характеристического уравнения строиться в зависимости от характера его корней.
Возможны три случая:
— дискриминант квадратного уравнения больше нуля D > 0 , уравнение имеет два действительный различных корня, k1≠ k2, и общее решение характеристического уравнения имеет вид:
— дискриминант характеристического квадратного уравнения равен нулю D= 0, уравнение имеет два действительный кратных корня, k1= k2= k, и общее решение уравнения имеет вид:
— дискриминант квадратного уравнения меньше нуля D 2 +7k+6=0.
Решим его: D=49-24=25, k1= -1, k2 = -6. Так как корни действительные и разные, то, согласно формулы , получаем общее решение:
Пример 10.9. Найти общее решение дифференциального уравнения
Решение. Составим характеристическое уравнение
Решим это уравнение: D = 36 -36 = 0, k1 = k2 =3. Характеристическое уравнение имеет два действительных кратных корня, следовательно, общее решение находим по формуле :
Пример 10.10. Найти общее решение дифференциального уравнения
Решение. Составим характеристическое уравнение
Решим его. Дискриминант квадратного уравнения меньше нуля, D=-36, уравнение имеет пару комплексно сопряженных корней , k1,2=
(α=2, β=3) и общее решение уравнения имеет вид:
Пример 10.11. Найти частное решение дифференциального уравнения
y»-5y’+4y=0, удовлетворяющее начальным условиям у'(0)=8, у(0)=5.
Решение. Сначала найдем общее решение, для этого составим
Дискриминант этого уравнения D=1, следовательно, уравнение имеет два действительный корня, k1 = 2, k2 = 3 и общее решение уравнения имеет вид:
Чтобы найти частное решение, сначала найдем у’=2С1e 2 x +3C2e 3 x , а затем подставим в общее решение и в производную от функции-решения у начальные условия и получим систему для определения постоянных С1 и С2 .

Таким образом искомое частное решение имеет вид: y =7e 2 x – 2e 3 x .
Не нашли, что искали? Воспользуйтесь поиском:
http://www.matematika.uznateshe.ru/odnorodnye-differencialnye-uravneniya-vtorogo-poryadka-s-postoyannymi-koefficientami/
http://vikidalka.ru/2-80241.html

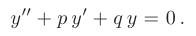
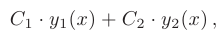
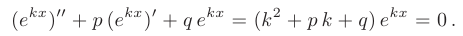
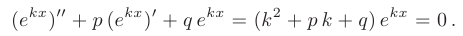
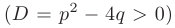 , то корни характеристического уравнения действительные, простые:
, то корни характеристического уравнения действительные, простые: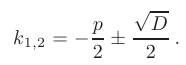
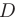 = 0), то корни характеристического уравнения действительные, кратные:
= 0), то корни характеристического уравнения действительные, кратные: