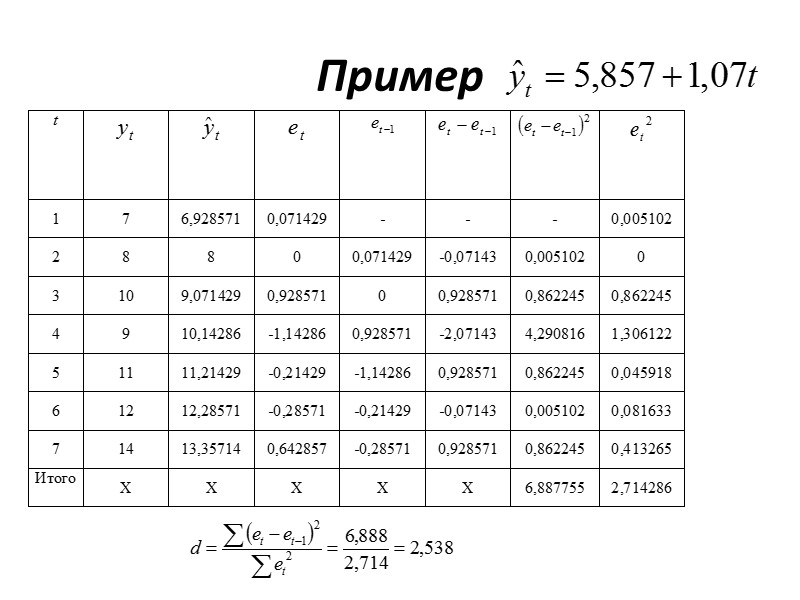
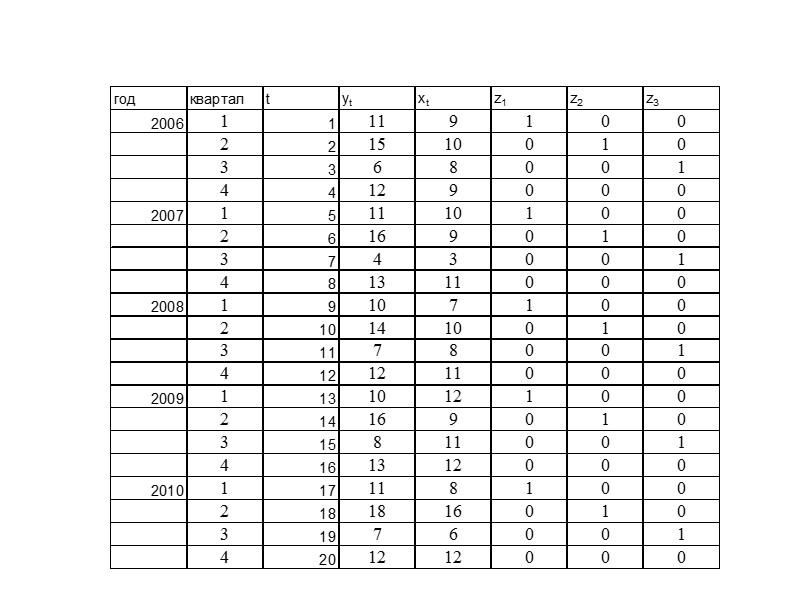
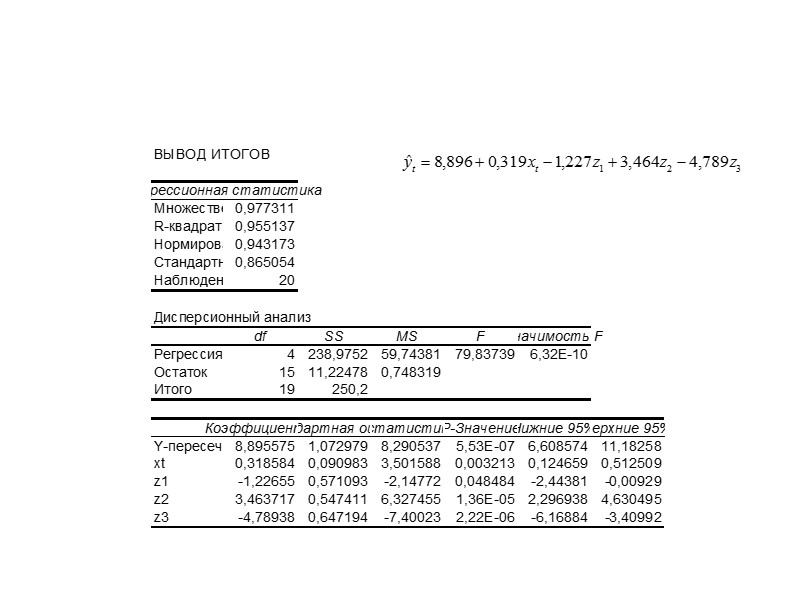
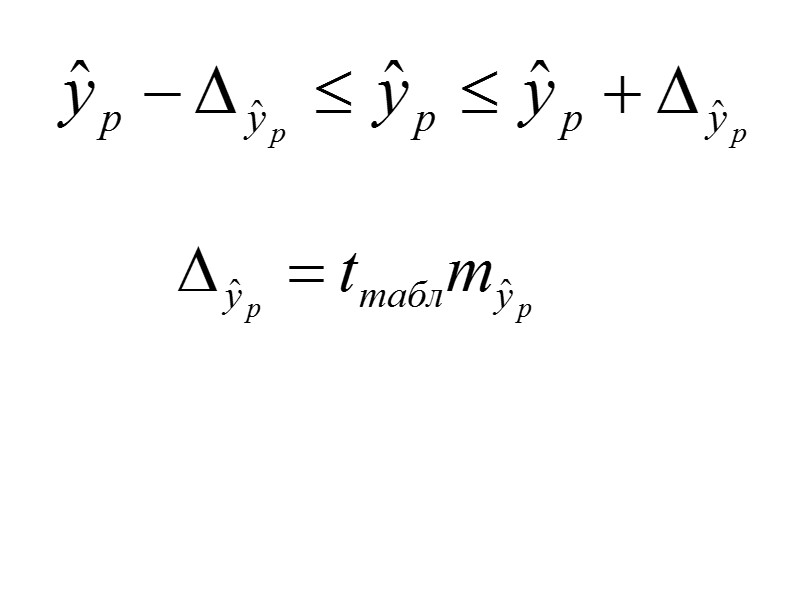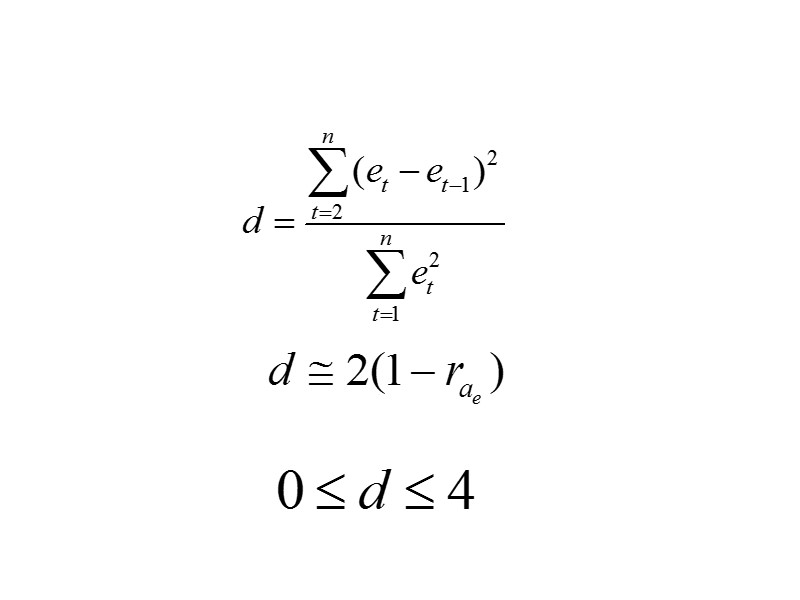Парная регрессия и корреляция
1. Парная регрессия и корреляция
1.1. Понятие регрессии
Парной регрессией называется уравнение связи двух переменных у и х
где у – зависимая переменная (результативный признак); х – независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессия описывается уравнением: y = a + b × x +e .
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Примеры регрессий, нелинейных по объясняющим переменным, но ли-
нейных по оцениваемым параметрам:
· полиномы разных степеней
· равносторонняя гипербола:
Примеры регрессий, нелинейных по оцениваемым параметрам:
· степенная
· показательная
· экспоненциальная
Наиболее часто применяются следующие модели регрессий:
– прямой
– гиперболы
– параболы
– показательной функции
– степенная функция
1.2. Построение уравнения регрессии
Постановка задачи. По имеющимся данным n наблюдений за совместным
изменением двух параметров x и y <(xi,yi), i=1,2. n> необходимо определить
аналитическую зависимость ŷ=f(x), наилучшим образом описывающую данные наблюдений.
Построение уравнения регрессии осуществляется в два этапа (предполагает решение двух задач):
– спецификация модели (определение вида аналитической зависимости
– оценка параметров выбранной модели.
1.2.1. Спецификация модели
Парная регрессия применяется, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.
Применяется три основных метода выбора вида аналитической зависимости:
– графический (на основе анализа поля корреляций);
– аналитический, т. е. исходя из теории изучаемой взаимосвязи;
– экспериментальный, т. е. путем сравнения величины остаточной дисперсии Dост или средней ошибки аппроксимации , рассчитанных для различных
моделей регрессии (метод перебора).
1.2.2. Оценка параметров модели
Для оценки параметров регрессий, линейных по этим параметрам, используется метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических значений ŷx при тех же значениях фактора x минимальна, т. е.
В случае линейной регрессии параметры а и b находятся из следующей
системы нормальных уравнений метода МНК:

Можно воспользоваться готовыми формулами, которые вытекают из этой

Для нелинейных уравнений регрессии, приводимых к линейным с помощью преобразования (x, y) → (x’, y’), система нормальных уравнений имеет
вид (1.1) в преобразованных переменных x’, y’.
Коэффициент b при факторной переменной x имеет следующую интерпретацию: он показывает, на сколько изменится в среднем величина y при изменении фактора x на 1 единицу измерения.
Линеаризующее преобразование: x’ = 1/x; y’ = y.
Уравнения (1.1) и формулы (1.2) принимают вид
Линеаризующее преобразование: x’ = x; y’ = lny.
Модифицированная экспонента: 
Степенная функция:
Линеаризующее преобразование: x’ = ln x; y’ = ln y.
Показательная функция:
Линеаризующее преобразование: x’ = x; y’ = lny.

Линеаризующее преобразование: x’ = ln x; y’ = y.
Парабола второго порядка:
Парабола второго порядка имеет 3 параметра a0, a1, a2, которые определяются из системы трех уравнений
1.3. Оценка тесноты связи
Тесноту связи изучаемых явлений оценивает линейный коэффициент
парной корреляции rxy для линейной регрессии (–1 ≤ r xy ≤ 1)
и индекс корреляции ρxy для нелинейной регрессии

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент детерминации r2xy (для линейной регрессии) или индекс детерминации (для нелинейной регрессии).
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
Для оценки качества построенной модели регрессии можно использовать
показатель (коэффициент, индекс) детерминации R2 либо среднюю ошибку аппроксимации.
Чем выше показатель детерминации или чем ниже средняя ошибка аппроксимации, тем лучше модель описывает исходные данные.
Средняя ошибка аппроксимации – среднее относительное отклонение
расчетных значений от фактических
Построенное уравнение регрессии считается удовлетворительным, если
значение не превышает 10–12 %.
1.4. Оценка значимости уравнения регрессии, его коэффициентов,
Оценка значимости всего уравнения регрессии в целом осуществляется с
помощью F-критерия Фишера.
F-критерий Фишера заключается в проверке гипотезы Но о статистической незначимости уравнения регрессии. Для этого выполняется сравнение
фактического Fфакт и критического (табличного) Fтабл значений F-критерия
Fфакт определяется из соотношения значений факторной и остаточной
дисперсий, рассчитанных на одну степень свободы
где n – число единиц совокупности; m – число параметров при переменных.
Для линейной регрессии m = 1 .
Для нелинейной регрессии вместо r 2 xy используется R2.
Fтабл – максимально возможное значение критерия под влиянием случайных факторов при степенях свободы k1 = m, k2 = n – m – 1 (для линейной регрессии m = 1) и уровне значимости α.
Уровень значимости α – вероятность отвергнуть правильную гипотезу
при условии, что она верна. Обычно величина α принимается равной 0,05 или
Если Fтабл Fфакт, то гипотеза Но не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов линейной регрессии и линейного коэффициента парной корреляции применяется
t-критерий Стьюдента и рассчитываются доверительные интервалы каждого
Согласно t-критерию выдвигается гипотеза Н0 о случайной природе показателей, т. е. о незначимом их отличии от нуля. Далее рассчитываются фактические значения критерия tфакт для оцениваемых коэффициентов регрессии и коэффициента корреляции путем сопоставления их значений с величиной стандартной ошибки
Стандартные ошибки параметров линейной регрессии и коэффициента
корреляции определяются по формулам

tтабл и tфакт принимают или отвергают гипотезу Но.
tтабл – максимально возможное значение критерия под влиянием случайных факторов при данной степени свободы k = n–2 и уровне значимости α.
Связь между F-критерием Фишера (при k1 = 1; m =1) и t-критерием Стьюдента выражается равенством
Если tтабл tфакт, то гипотеза Но не отклоняется и признается случайная природа формирования а, b или 
Значимость коэффициента детерминации R2 (индекса корреляции) определяется с помощью F-критерия Фишера. Фактическое значение критерия Fфакт определяется по формуле
Fтабл определяется из таблицы при степенях свободы k1 = 1, k2 = n–2 и при
заданном уровне значимости α. Если Fтабл
Оценка значимости уравнения множественной регрессии (F-критерий): Если Fфакт
Оценка значимости уравнения множественной регрессии (F-критерий): Если Fфакт > Fтабл, то признается статистическая значимость» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_0.jpg» alt=»>Оценка значимости уравнения множественной регрессии (F-критерий): Если Fфакт > Fтабл, то признается статистическая значимость» /> Оценка значимости уравнения множественной регрессии (F-критерий): Если Fфакт > Fтабл, то признается статистическая значимость и надежность уравнения. Если Fфакт » />
частный F-критерий Во множественной регрессии оценивается значимость не только уравнения в целом, но и» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_2.jpg» alt=»>частный F-критерий Во множественной регрессии оценивается значимость не только уравнения в целом, но и» /> частный F-критерий Во множественной регрессии оценивается значимость не только уравнения в целом, но и фактора, дополнительно включенного в регрессионную модель. Это связано с тем, что не каждый фактор, вошедший в модель, может существенно увеличивать долю объясненной вариации результативного признака. Ввиду корреляции между факторами значимость одного и того же фактора может быть разной в зависимости от последовательности его введения в модель. Мерой для оценки включения фактора в модель служит частный F-критерий, т.е. Fxi.
Частный F-критерий Частные критерии Fx1 оценивает статистическую значимость включения фактора x1 в» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_3.jpg» alt=»>Частный F-критерий Частные критерии Fx1 оценивает статистическую значимость включения фактора x1 в» /> Частный F-критерий Частные критерии Fx1 оценивает статистическую значимость включения фактора x1 в уравнение множественной регрессии после другого фактора , т.е. Fx1 оценивает целесообразность включения в уравнение x1 после включения в него, например, фактора x2.
Методика построения Fxj Частный F-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_4.jpg» alt=»>Методика построения Fxj Частный F-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно» /> Методика построения Fxj Частный F-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. Предположим, что для регрессии с двумя факторами оцениваем значимость влияния Х1 как дополнительно включенного в модель фактора. Используем следующую формулу:
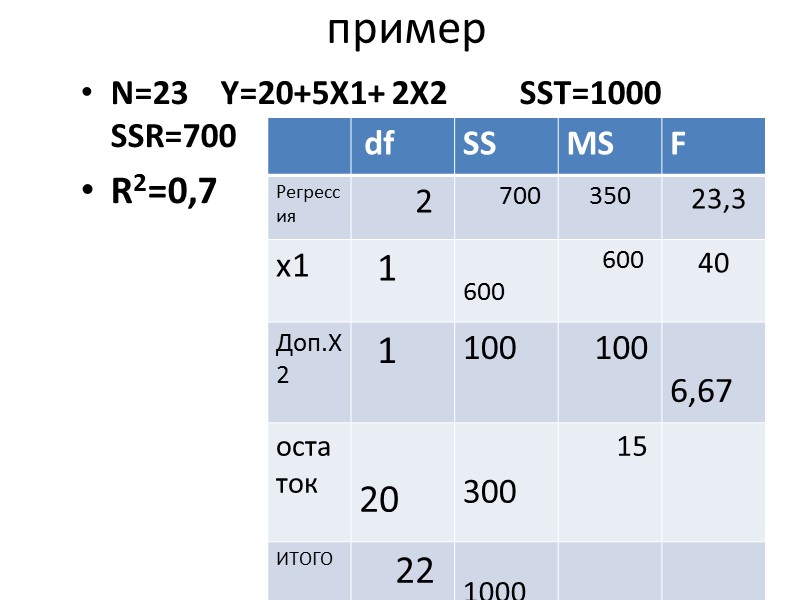
пример N=23 Y=20+5X1+ 2X2 » src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_6.jpg» alt=»>пример N=23 Y=20+5X1+ 2X2 » /> пример N=23 Y=20+5X1+ 2X2 SST=1000 SSR=700 R2=0,7 r2yx1=0,6
Fx2 Fx2 =(0,7-0,6) x 20/0,3 =6,67 F(a=0,05; 1 и 20)=4,35″ src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_7.jpg» alt=»>Fx2 Fx2 =(0,7-0,6) x 20/0,3 =6,67 F(a=0,05; 1 и 20)=4,35″ /> Fx2 Fx2 =(0,7-0,6) x 20/0,3 =6,67 F(a=0,05; 1 и 20)=4,35
Зная величину Fxi можно определить и t – критерий для коэффициента регрессии при i-том» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_8.jpg» alt=»>Зная величину Fxi можно определить и t – критерий для коэффициента регрессии при i-том» /> Зная величину Fxi можно определить и t – критерий для коэффициента регрессии при i-том факторе.
связь частного Fкритерия Частный F-критерий связан с частной корреляцией. Частный F-критерий в числителе» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_9.jpg» alt=»>связь частного Fкритерия Частный F-критерий связан с частной корреляцией. Частный F-критерий в числителе» /> связь частного Fкритерия Частный F-критерий связан с частной корреляцией. Частный F-критерий в числителе формулы содержит прирост факторной дисперсии, т.е сокращение остаточной дисперсии, которая учитывается в частной корреляции. Поэтому отсев факторов при построении модели множественной регрессии возможен при использовании как частной корреляции, так и частного F-критерия, а также t-критерия Стьюдента и стандартизованных коэффициентов регрессии (β).
Прогноз по множественной регрессии» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_10.jpg» alt=»>Прогноз по множественной регрессии» /> Прогноз по множественной регрессии
Модели на основе рядов динамики Модели изолированного динамического ряда. Модели системы взаимосвязанных рядов» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_12.jpg» alt=»>Модели на основе рядов динамики Модели изолированного динамического ряда. Модели системы взаимосвязанных рядов» /> Модели на основе рядов динамики Модели изолированного динамического ряда. Модели системы взаимосвязанных рядов динамики. Модели автрегрессии. Модели с распределенным лагом.
Компоненты временного ряда Тенденция (T) Периодические колебания (P) Случайные колебания (E)» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_13.jpg» alt=»>Компоненты временного ряда Тенденция (T) Периодические колебания (P) Случайные колебания (E)» /> Компоненты временного ряда Тенденция (T) Периодические колебания (P) Случайные колебания (E)
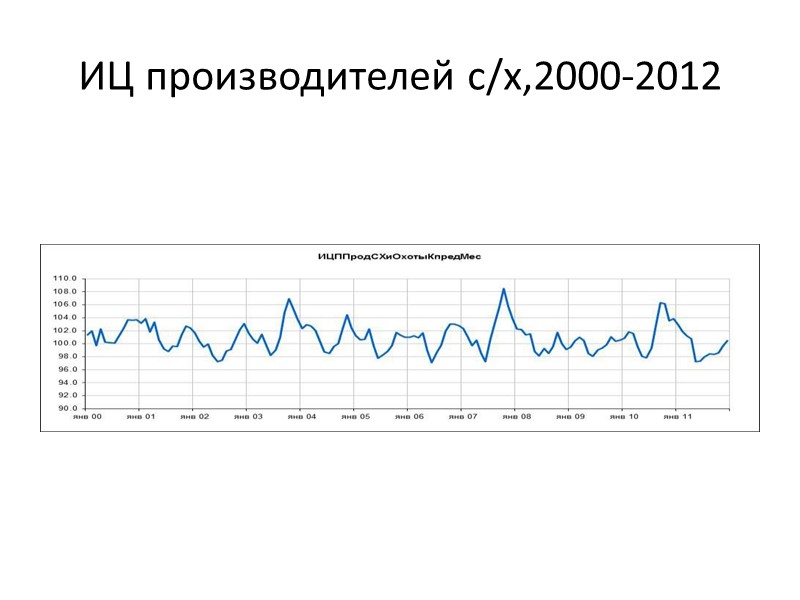
ИЦ производителей с/х,2000-2012″ src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_14.jpg» alt=»>ИЦ производителей с/х,2000-2012″ /> ИЦ производителей с/х,2000-2012
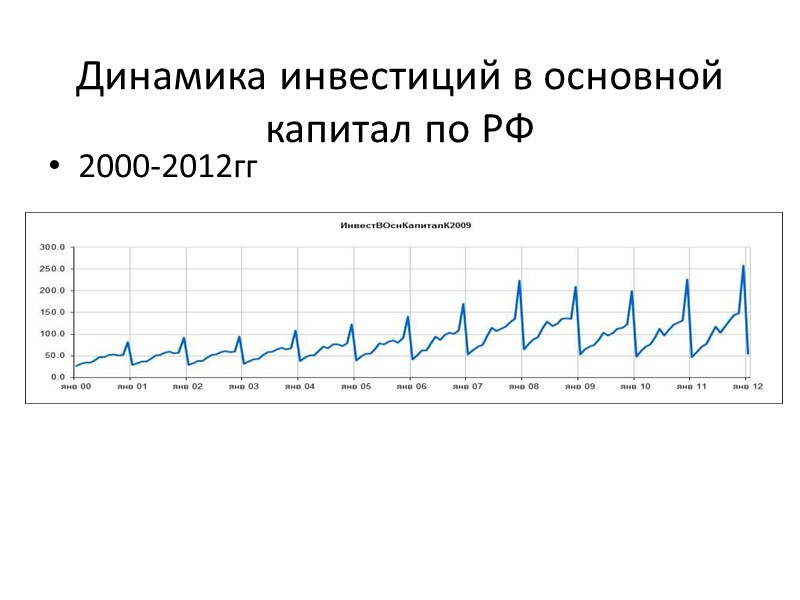
Динамика инвестиций в основной капитал по РФ 2000-2012гг» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_15.jpg» alt=»>Динамика инвестиций в основной капитал по РФ 2000-2012гг» /> Динамика инвестиций в основной капитал по РФ 2000-2012гг
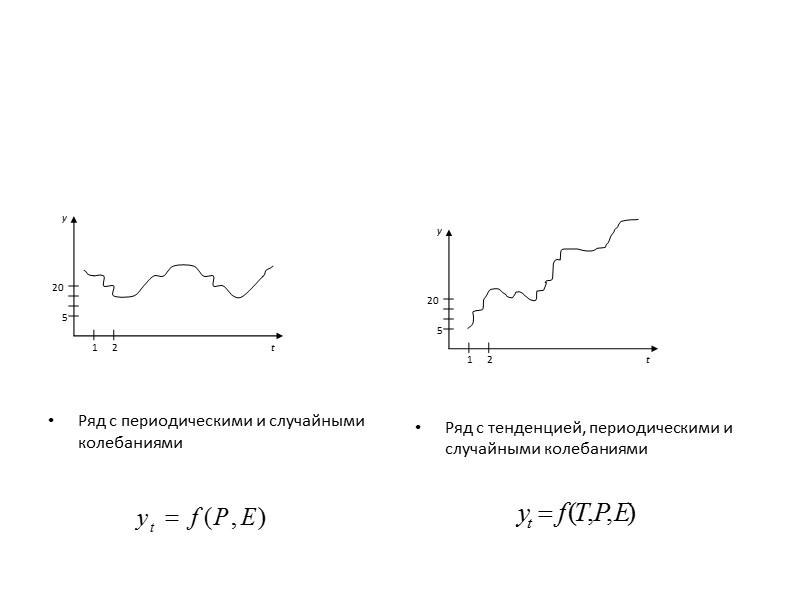
Ряд с периодическими и случайными колебаниями Ряд» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_16.jpg» alt=»>Ряд с периодическими и случайными колебаниями Ряд» /> Ряд с периодическими и случайными колебаниями Ряд с тенденцией, периодическими и случайными колебаниями
Аддитивная модель Мультипликативная модель» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_17.jpg» alt=»>Аддитивная модель Мультипликативная модель» /> Аддитивная модель Мультипликативная модель
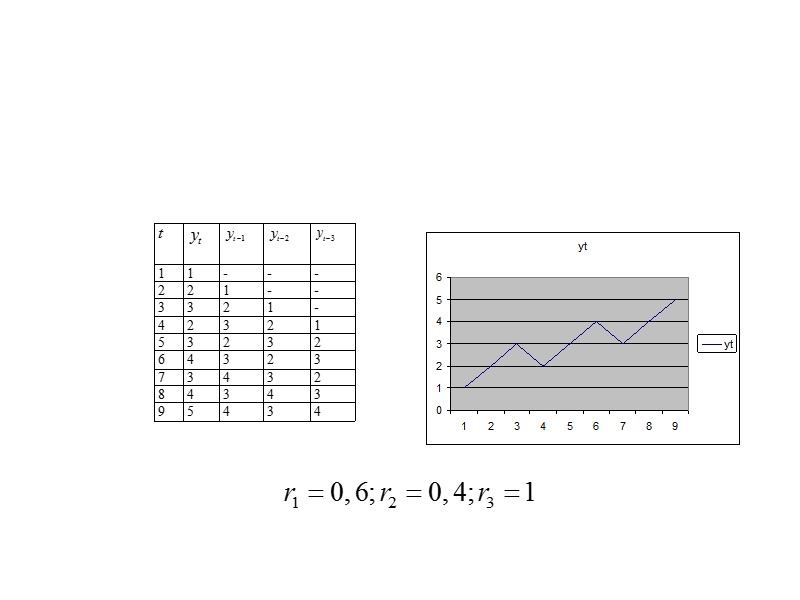
Автокорреляция уровней ряда и ее последствия Корреляционная зависимость между последовательными значениями уровней временного ряда» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_18.jpg» alt=»>Автокорреляция уровней ряда и ее последствия Корреляционная зависимость между последовательными значениями уровней временного ряда» /> Автокорреляция уровней ряда и ее последствия Корреляционная зависимость между последовательными значениями уровней временного ряда называется автокорреляцией уровней ряда
Уравнения трендов» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_20.jpg» alt=»>Уравнения трендов» /> Уравнения трендов
Линейный тренд» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_21.jpg» alt=»>Линейный тренд» /> Линейный тренд
Линейный тренд :Y=a+bt равным абсолютным приростом (параметр b) индекс потребительских цен за 12″ src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_22.jpg» alt=»>Линейный тренд :Y=a+bt равным абсолютным приростом (параметр b) индекс потребительских цен за 12″ /> Линейный тренд :Y=a+bt равным абсолютным приростом (параметр b) индекс потребительских цен за 12 месяцев = 100,5 + 2t, где t = 1, 2,…, 12 у1=102,5; у12=124,5
Парабола 2-го порядка» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_23.jpg» alt=»>Парабола 2-го порядка» /> Парабола 2-го порядка
Парабола :Y=a+bt+ct2 постоянное абсолютное ускорение(∆2) параметр «а»−У при t=0 Параметр «с»=0,5(∆2)» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_24.jpg» alt=»>Парабола :Y=a+bt+ct2 постоянное абсолютное ускорение(∆2) параметр «а»−У при t=0 Параметр «с»=0,5(∆2)» /> Парабола :Y=a+bt+ct2 постоянное абсолютное ускорение(∆2) параметр «а»−У при t=0 Параметр «с»=0,5(∆2)
численность детей в возрасте 7 лет за 15 лет Y=323.7+10.8t-1.6t^2, где y – тыс.» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_25.jpg» alt=»>численность детей в возрасте 7 лет за 15 лет Y=323.7+10.8t-1.6t^2, где y – тыс.» /> численность детей в возрасте 7 лет за 15 лет Y=323.7+10.8t-1.6t^2, где y – тыс. чел., t = 1, 2,…, 15. ежегодно численность детей сокращалась в среднем с ускорением в 3,2 тыс. чел.
Показательная функция» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_26.jpg» alt=»>Показательная функция» /> Показательная функция
Показательная функция Y=ab^t стабильный коэффициент роста (b) Y=13.5*1.5^t Y=13.5e^0.405t−экспонента» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_27.jpg» alt=»>Показательная функция Y=ab^t стабильный коэффициент роста (b) Y=13.5*1.5^t Y=13.5e^0.405t−экспонента» /> Показательная функция Y=ab^t стабильный коэффициент роста (b) Y=13.5*1.5^t Y=13.5e^0.405t−экспонента
Степенной тренд При b > 0 она характеризует непрерывный рост уровней с падающими» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_28.jpg» alt=»>Степенной тренд При b > 0 она характеризует непрерывный рост уровней с падающими» /> Степенной тренд При b > 0 она характеризует непрерывный рост уровней с падающими темпами роста, а при b 0 означает, что уровни ряда снижаются во времени» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_29.jpg» alt=»>Равносторонняя гипербола при b > 0 означает, что уровни ряда снижаются во времени» /> Равносторонняя гипербола при b > 0 означает, что уровни ряда снижаются во времени и асимптотически приближаются к параметру а.Так,выручка предприятия за 7 месяев У=400+85/t ,т.е. падающая тенденция, при которой У не может быть меньше 400. Если b » />
Оценка параметров уравнения тренда При использовании полиномов разных степеней оценка параметров уравнения тренда производится» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_31.jpg» alt=»>Оценка параметров уравнения тренда При использовании полиномов разных степеней оценка параметров уравнения тренда производится» /> Оценка параметров уравнения тренда При использовании полиномов разных степеней оценка параметров уравнения тренда производится методом наименьших квадратов (МНК) точно также, как оценки параметров уравнения регрессии на основе пространственных данных. В качестве зависимой переменной -уровни динамического ряда, а в качестве независимой переменной – фактор времени t, который обычно выражается рядом натуральных чисел: 1, 2,…, n.
нелинейные функции тренла Оценка параметров нелинейных функций проводится МНК после линеаризации, т. е.» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_32.jpg» alt=»>нелинейные функции тренла Оценка параметров нелинейных функций проводится МНК после линеаризации, т. е.» /> нелинейные функции тренла Оценка параметров нелинейных функций проводится МНК после линеаризации, т. е. приведения их к линейному виду.
Показательная функция Для оценки параметров показательной кривой Y=ab^t или экспоненты Y=ae^bt путем логарифмирования» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_33.jpg» alt=»>Показательная функция Для оценки параметров показательной кривой Y=ab^t или экспоненты Y=ae^bt путем логарифмирования» /> Показательная функция Для оценки параметров показательной кривой Y=ab^t или экспоненты Y=ae^bt путем логарифмирования функции приводятся к линейному виду и применяется МНК к ln Y и t Число зарегистрированных ДТП (на 100000 человек населения) по области за 2005-2013 годы характеризуется данными:105,7; 105,3; 156; 158,1; 160,1; 178; 191,5; 274,6; 287,3.
Для построения системы нормальных уравнений были рассчитаны вспомогательные величины:ln Y получим: ln Y= 4,517598″ src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_34.jpg» alt=»>Для построения системы нормальных уравнений были рассчитаны вспомогательные величины:ln Y получим: ln Y= 4,517598″ /> Для построения системы нормальных уравнений были рассчитаны вспомогательные величины:ln Y получим: ln Y= 4,517598 + 0,123523t, где 4,517598= lna 0,123523=lnb a = e4,5176 = 91,61524 b = e0,12352 = 1,131476 Соответственно, имеем экспоненту y=91,615e0,1235t или показательную кривую: Y=91,615*1,1315t. Число ДТПвозрастало в среднем ежегодно на 13,5%.
Использование трендовых моделей для прогнозирования» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_35.jpg» alt=»>Использование трендовых моделей для прогнозирования» /> Использование трендовых моделей для прогнозирования
Y=13.028+3.0167t t=1.2….9мес. tp =10 Ур=43,19 √ МSост =(14,87/7″ src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_36.jpg» alt=»>Y=13.028+3.0167t t=1.2….9мес. tp =10 Ур=43,19 √ МSост =(14,87/7″ /> Y=13.028+3.0167t t=1.2….9мес. tp =10 Ур=43,19 √ МSост =(14,87/7 )0,5=1,4576-cтандартная ошибка регрессии; Q=(1+(1/9)+(10-5)^2/60)^0,5=1.236 Sp =1,4576* 1.236=1.801- ошибка прогноза a=0.05 ; df=7 ; ta = 2,365 ; ∆р=2,365*1,801=4,26-предельная ошибка прогноза 43,19 ± 4,26 , т .е интервал от 38,9 до 47,4.
Оценка адекватности модели тенденции Модель тенденции считается адекватной реальному процессу, если теоретические (найденные по» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_37.jpg» alt=»>Оценка адекватности модели тенденции Модель тенденции считается адекватной реальному процессу, если теоретические (найденные по» /> Оценка адекватности модели тенденции Модель тенденции считается адекватной реальному процессу, если теоретические (найденные по уравнению тренда) уровни ряда достаточно близко подходят к фактическим их значениям. Для оценки адекватности модели проводится анализ остатков . Модели тенденции можно сравнивать по величине остаточной суммы квадратов:S^2=∑(Y – Yteor)^2. Чем меньше эта величина, тем в большей мере уравнение тренда подходит для описания тенденции временного ряда.
Предположим, что было рассчитано уравнение линейного тренда и экспоненциального тренда. Для линейного тренда» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_38.jpg» alt=»>Предположим, что было рассчитано уравнение линейного тренда и экспоненциального тренда. Для линейного тренда» /> Предположим, что было рассчитано уравнение линейного тренда и экспоненциального тренда. Для линейного тренда остаточная сумма квадратов составила 3874,62, а для экспоненты 2617,701. Следовательно, экспонента лучше описывает тенденцию ряда. Другим показателем при выборе функции тренда является коэффициент детерминации R2. Чем выше R2, тем соответственно выше вероятность того, что данная модель тенденции описывает исходные данные. В примере R2 для экспоненты составил 0,9202, а для линейного тренда 0,8832, подтверждая еще раз, что экспонента в большей мере подходит для описания тенденции.
Автокорреляция в остатках» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_39.jpg» alt=»>Автокорреляция в остатках» /> Автокорреляция в остатках
автокорреляция в остатках оценивается также, как и автокорреляция уровней ряда с тем лишь отличием,» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_40.jpg» alt=»>автокорреляция в остатках оценивается также, как и автокорреляция уровней ряда с тем лишь отличием,» /> автокорреляция в остатках оценивается также, как и автокорреляция уровней ряда с тем лишь отличием, что в расчетах используются остаточные величины , а не уровни динамического ряда .Пусть коэффициент автокорреляции остатков оказался равным 0,627. Его величина не столь мала, чтобы утверждать об отсутствии автокорреляции остатков. Очевидно уравнение тренда не является наилучшим, ибо нарушена предпосылка МНК об отсутствии автокорреляции остатков.
Уравнение тренда хорошо описывает тенденцию, если остатки текущего периода не коррелируют с остатками предыдущего» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_41.jpg» alt=»>Уравнение тренда хорошо описывает тенденцию, если остатки текущего периода не коррелируют с остатками предыдущего» /> Уравнение тренда хорошо описывает тенденцию, если остатки текущего периода не коррелируют с остатками предыдущего периода. Проверка модели на автокорреляцию остатков обычно проводится с помощью критерия Дарбина-Уотсона.
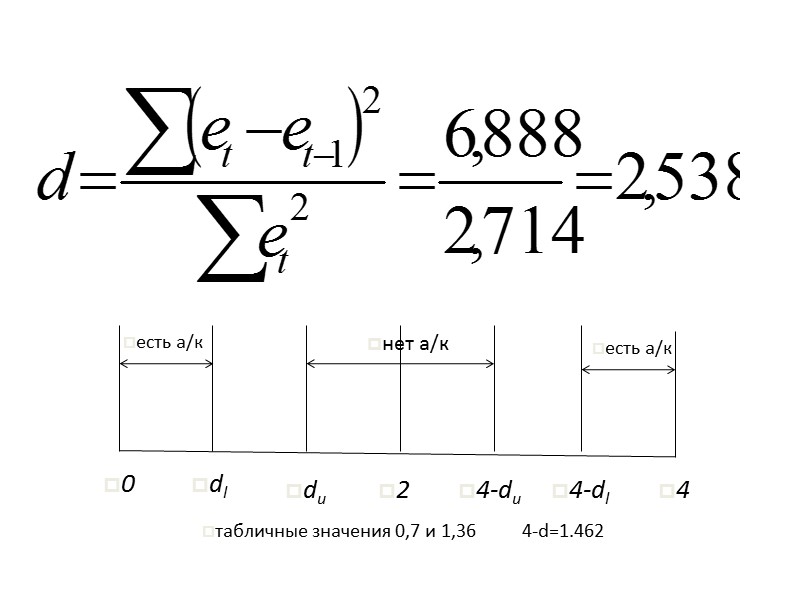
Границы критерия Дарбина-Уотсона При полной положительной автокорреляции остатков (ρ=1 ) критерий » src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_43.jpg» alt=»>Границы критерия Дарбина-Уотсона При полной положительной автокорреляции остатков (ρ=1 ) критерий » /> Границы критерия Дарбина-Уотсона При полной положительной автокорреляции остатков (ρ=1 ) критерий d=0, а при полной отрицательной автокорреляции (ρ=−1 ) критерий d=4. Если же автокорреляция в остатках отсутствует, т. е. ρ=0 , то d=2. Иными словами критерий Дарбина-Уотсона изменяется в пределах: 0≤ d ≤ 4.
Дарбин и Уотсон разработали пороговые значения показателя d, позволяющие принять или отвергнуть гипотезу об» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_44.jpg» alt=»>Дарбин и Уотсон разработали пороговые значения показателя d, позволяющие принять или отвергнуть гипотезу об» /> Дарбин и Уотсон разработали пороговые значения показателя d, позволяющие принять или отвергнуть гипотезу об отсутствии автокорреляции в остатках. При заданном числе наблюдений n (длина динамического ряда) и m параметров при t в уравнении тренда (или m объясняющих переменных в уравнении регрессии) установлены при 5%-ом уровне значимости верхняя (u – upper) и нижняя (ℓ ‑ low) границы критерия.
сравнение с табличными значениями Если d сравнение с табличными значениями Если d сравнение с табличными значениями Если d фактическое значение d › 2 означает отрицательную автокорреляцию, то с пороговыми табличными значениями сравнивается» /> фактическое значение d › 2 означает отрицательную автокорреляцию, то с пороговыми табличными значениями сравнивается величина 4-d. При этом возможны следующие варианты: 1) 4-d ‹ нижней границы: делается вывод о наличии отрицательной автокорреляции в остатках; 2)4-d › верхней границы: отсутствует автокорреляция в остатках; 3) 4-d между нижней и верхней границами: нельзя сделать определенного вывода о наличии или отсутствии автокорреляции в остатках по имеющимся данным
Линейная модель парной регрессии.
Уравнение парной линейной регрессии имеет вид:

у – зависимая переменная;
х – независимая (объясняющая) переменная;
а и b – параметры уравнения;

Метод наименьших квадратов для парной регрессии записывается в виде системы (2)
(2)
Решаем ее и находим коэффициенты a и b. Можно вычислять коэффициенты по формулам (3), которые легко получаются из (2)



Параметр »b» называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Параметр »а» не имеет экономического содержания. Интерпретировать можно лишь знак при параметре «а». Если а>0, то относительное изменение результата происходит медленнее, чем изменение фактора, т.е. изменение Var (y) Vx ) или a > 0 (Vy 2


Сначала заполним первые 6 столбцов, а затем составим систему для МНК, и определим параметры а и b

решая которую любым способом, получим:

подставляя в (1) значение х из столбика 2, вычислим 
Коэффициент корреляции можно вычислить и по следующим формулам
Связь между х и у прямая, весьма высокая.
Оценку качества полученной модели дает коэффициент детерминации 
О качестве модели судят по средней ошибке аппроксимации, которая

показывает среднее отклонение расчетных значений от фактических. Допустимый предел значений Ā – не более 8-10%. У нас 
Задача 4.
Для количественного анализа влияния доходности акций компании лидера на доходности акций других компаний применяются методы регрессивного анализа. Построить модель парной регрессии для изучения зависимости доходности акций компании А от доходности акций компании Б. Компании А и Б относятся к одной отрасли, данные по годовым доходностям акций приведены в таблице:
| Номер наблюдения | Доходность акций А (у), % | Доходность акций Б (х), % |
| -2,56 26,65 4,44 17,12 10,19 13,88 4,55 10,28 11,76 11,89 5,14 7,70 7,17 7,57 17,46 | -5,31 16,84 0,07 10,03 4,98 7,52 0,23 5,30 5,94 6,09 0,93 3,22 2,08 2,81 10,73 |
Ответ: 
Задача 5.
Построить две модели парной регрессии зависимости годового товарооборота фирмы (млн. руб.) – у от размера торговой площади (тыс. кв. м) – х1 и – х2. Исходные данные приведены в таблице:
| № филиала | Товарооборот (уi) | Торговая площадь (х1) | Интенсивность потока покупателей (х2) |
| 2,93 5,29 6,85 7,01 7,02 8,35 4,33 5,77 7,68 3,16 1,52 3,15 | 0,31 0,98 1,21 1,29 1,12 1,49 0,78 0,94 1,29 0,48 0,24 0,55 | 10,24 7,51 10,81 9,89 13,72 13,92 8,54 12,36 12,27 11,01 8,25 9,31 |
Ответ: 1) 
Дисперсионный анализ. Критерии Фишера и Стьюдента.
Оценка степени тесноты связи и существенности параметров линейной регрессии. Критерии Фигнера и Стьюдента.
| Общая сумма квадратов отклонения | = | Сумма квадратов отклонений, объясненная регрессией | + | Остаточная сумма квадратов отклонений |
| TSS | = | ESS | + | RSS |
Чем выше R 2 , тем выше доля объясненной моделью регрессии (ESS) по отношению к полной сумме квадратов (TSS).
Задача 6.
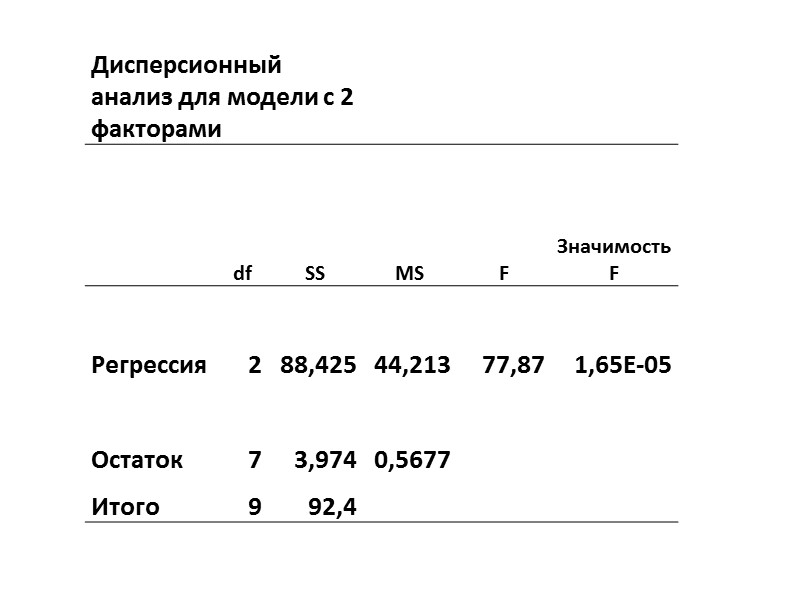
Для задачи 3 выполнить дисперсионный анализ

| Источники вариации | Число степеней свободы | Сумма квадратов отклонений | Дисперсия на 1 степень свободы | F отн |
| Факт. | Табл. α=0,05 | |||
| Общая TSS |  | – | – | – |
| Объясн. ESS | 1 (к1) | 6,61 | ||
| Остаточн. RSS |  (к2) (к2) |
Критерий Фишера равен:
Fфакт> Fтабл. как при 5%, так и при 1% уровне значимости уравнения регрессии. 
Объясненную сумму квадратов (ESS) можно вычислить как 
Тогда значение критерия Фишера
Задача 7.
Для задачи 4 вычислить коэффициент детерминации R 2 и Fфакт (Ответ: R 2 = 0.9965)
Задача 8.
Для задачи 5 вычислить R1 2 и R2 2 , сравнить, объяснить различие и выбрать лучшее уравнение регрессии, объяснить почему.
Ответ: R1 2 = 0,96886, R2 2 = 0,42433, первое уравнение лучше.
В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров и коэффициенту регрессии определяется его стандартная ошибка: mb и ma, mr
Выдвигается гипотеза 
Затем сравнивая фактическое и критическое (табличное значения t-статистики принимаем или отвергаем гипотезу 
Если tтабл табличного, то гипотезу о несущественности коэффициента регрессии »b» можно отклонить. Доверительный интервал для коэффициента регрессии определяется как

-0,7752>-2,75, т.е. коэффициент «а» статистически не значим, т.е. Но не отклоняется. Доверительный интервал для «а» не определяется.
Значимость линейного коэффициента корреляции определим на основе величины ошибки mr

Рассмотренная формула для тr рекомендуется к применению при большом числе наблюдений и если r не близко к +1 или -1. Если корреляция близка к +1, то распределение его оценок отличается от нормального или распределения Стьюдента, т.к. величина rxy ограничена значениями. Р. Фишер предложил для оценки вклада rxy ввести вспомогательную величину z, связанную с rxy следующим отношением:
При изменении r от -1 до +1 z изменяется от 


В нашем примере 

Для вычисления величины z есть таблицы z-преобразований, приложения III из [11], для числа степеней свободы 


Если не пользоваться таблицами, то стандартную ошибку можно определить


6. Стандартная ошибка уравнения регрессии. Прогнозное значение.
В прогнозных расчетах по уравнению регрессии можно определить предсказываемое значение (ур) как точечный прогноз 



Стандартная ошибка 





Этот доверительный интервал получился без учета случайной ошибки 
Доверительный интервал в этом случае будет
Задача 9. Наблюдения 16 пар (Х и Y) дали следующие результаты:

Оцените регрессию 
1. Оценим параметры регрессии
Оценка дисперсии ошибок равна
2. Проверка гипотезы Н1:
Оценка дисперсии b:

Для проверки гипотезы Н1 найдем:


Поэтому Н1: 





Задача 10. Получена регрессионная зависимость расходов на питание от располагаемого личного дохода населения США за 25-летний срок (1959-1983 гг.). Уравнение регрессии имеет вид:
Цифры в скобках есть стандартные ошибки.
Сформулируем Н0: b0=0 и попытаемся ее опровергнуть



Критерий можно записать в виде неравенств:
| -2,069 |
| но |
| +2,069 |
| 31,0 |


Для параметра «а»
Коэффициент «а» статистически значим.
Задача 11. Модель зависимость между общей инфляцией и инфляцией, вызванной ростом заработной платы имеет вид (в скобках указаны стандартные ошибки)
Проверить значимость коэффициентов «а» и «b», если число наблюдений 
Ответ:
Задача 12. Уравнения регрессии между расходами на коммунальные услуги и (1) располагаемым личным доходом и (2) временем за период с 1959г. по 1983г. в США имеют вид:


В скобках указаны стандартные ошибки.
Выполните t-тест для проверки значимости коэффициентов.
http://present5.com/ocenka-znachimosti-uravneniya-mnozhestvennoj-regressii-f-kriterij-esli-ffakt/
http://poisk-ru.ru/s33780t14.html