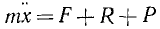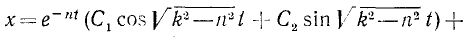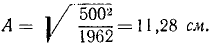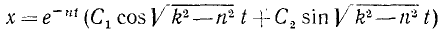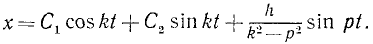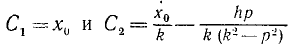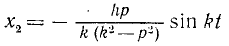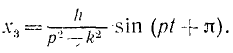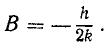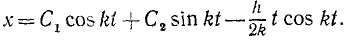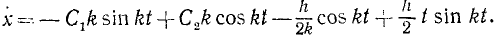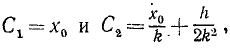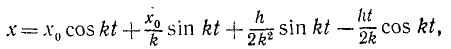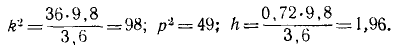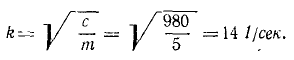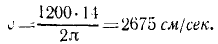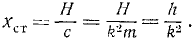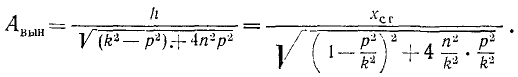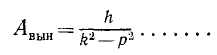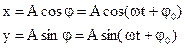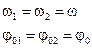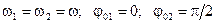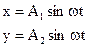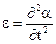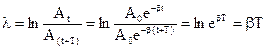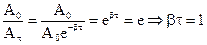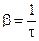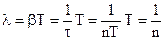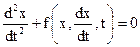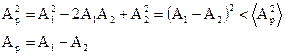Если колебание сложное то его уравнение

Колебания материальной точки в теоретической механике

Содержание:

Колебания материальной точки:

К исследованию колебаний одной материальной точки могут быть сведены многие технические задачи

В качестве примера интегрирования дифференциальных уравнений движения рассмотрим колебания материальной точки. Еще совсем недавно изучение колебаний не входило в программу курсов теоретической механики высших учебных заведений. Но необходимость создания новых методов расчета всевозможных машин и различных сооружений, обладающих большой прочностью при небольшом весе, а также необходимость увеличения скоростей и производигельности машин стимулировали быстрое развитие раздела динамики, называемого теорией колебаний. Раздел, посвященный колебаниям, включен теперь во все программы по теоретической механике.

C основами явлений колебаний удобно ознакомиться сперва на примере, колебания одной материальной точки. Изучение вибраций одной материальной точки интересно также и потому, что к вибрации точки могут быть непосредственно приведены многие практически важные задачи.

Пусть точка M массы m притягивается к точке О силой F, пропорциональной (рис. 162) расстоянию ОМ, а начальная скорость точки M направлена по прямой OM или равна нулю. В таком случае точка M будет двигаться по прямолинейной траектории, вдоль которой мы направим ось х. Начало координат возьмем в точке О (в равновесном положении). Сила F как бы стремится вернуть точку M в равновесное положение О, за что ее называют восстанавливающей силой. Примером такой силы могут служить сила упругости стержня, совершающего малые колебания, или равнодействующая сил веса G и натяжения T нити при малых колебаниях маятника и т. и. Чем больше координата х, тем больше величина этой силы. Вместе с тем сила (точнее говоря, ее проекция на ось Ох) по знаку всегда противоположна знаку координаты х. В самом деле, если точка M находится справа от x начала координат О, то координата х положительна, а сила направлена в отрицательную сторону, и наоборот, если координата х отрицательна, то восстанавливающая сила направлена в положительную сторону. Обозначив коэффициент пропорциональности между силой и расстоянием через с (причем с > 0), выразим восстанавливающую силу формулой

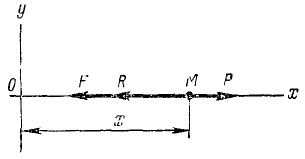
Рис. 162

Пусть на точку M во время ее движения действует сила сопротивления R, пропорциональная скорости точки и направленная против скорости. Таким образом, если точка M движется вправо (х > 0), то сила сопротивления направлена влево (R 0. Обозначив коэффициент пропорциональности через а (причем а > 0), мы определим силу сопротивления (выражаясь точнее, ее проекцию на ось Ох) формулой

Кроме того, пусть на точку M действует возмущающая сила Р, т. е. некоторая дополнительная сила, вызывающая изменение движения, обусловленного основной силой F. Возмущающая сила направлена по прямолинейной траектории точки M и, периодически изменяя свою величину и знак, раскачивает точку M то в ту, то в другую сторону. Мы ограничимся рассмотрением простейшего случая и предположим, что сила P изменяется с течением времени по закону синуса:

P = H sin pt. (133)

Очевидно, что сила P изменяется в пределах от +Н до —Н. Пример такой силы приведен в задаче № 110.

Напишем дифференциальное уравнение движения точки M:

Разделив обе части уравнения на т, введем обозначения

(134)

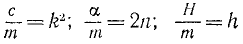
и перенесем члены, содержащие х или его производные, влево:

х + 2nx + k 2 x =h sin pt. (135)

Мы имеем неоднородное линейное дифференциальное уравнение с постоянными коэффициентами. Общее решение такого уравнения складывается из: 1) общего решения соответствующего однородного уравнения, т. е. уравнения (135) без правой части, и какого-либо частного решения неоднородного уравнения (135).

Для интегрирования уравнения

х + 2nx + k 2 x = 0

составим характеристическое уравнение

z 2 + 2nz + k 2 = 0.

Если n 2 sin (pt— δ)

и подставим в (135) написанное выражение х и его производных:

— Bp 2 sin (pt — δ) + 2nBp cos (pt — δ) + k 2 B sin (pt — δ) = h sin pt.

Преобразуем правую часть этого равенства:

h sin pt = h sin (pt — δ +δ) = h sin (pt — δ) cos ∂ + h cos (pt — δ) sin δ.

Перенеся все члены влево и собирая члены, содержащие sin(pt— δ) и cos (pt — δ), получим

[В (k 2 —p 2 )-h cos δ] sin (pt — δ) + (2Bnp-hsin δ) cos (pt — δ) = O.

Это равенство обращается в тождество, если

В (k 2 — р 2 ) = h cos δ; 2Bnp = h sin δ,

(137)

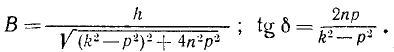
Складывая общее решение (136) однородного уравнения с найденным частным решением неоднородного уравнения, получим общее решение неоднородного уравнения (135) в таком виде:

(138)

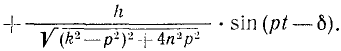
Прежде чем исследовать сложное колебательное движение точки под действием сил F, R и P, выражаемое уравнением (138), рассмотрим более простые движения, которые точка совершала’ бы под действием одной силы F или же под действием силы F и какой-либо- одной из двух остальных R или Р.

Точка, движущаяся по прямой, совершает под действием восстанавливающей силы гармоническое колебание

Свободные колебания без сопротивления

Предположим, что на материальную точку M (см. рис. 162 на стр. 274) действует только восстанавливающая сила (131), сила же сопротивления (132) и возмущающая сила (133) равны нулю. Пусть начальная скорость точки M направлена по прямой MO или равна нулю. В таком случае точка M будет двигаться по прямой OM (по оси Ох), дифференциальное и кинематическое уравнения ее движения мы получим, положив в (135) и в (138) n и h равными нулю. В самом деле, если сила сопротивления R=O, то, следовательно, α = 0, потому что R=— ах и х переменная величина. Если же a = 0, то равно нулю и n, которое согласно (134) равно 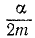. Аналогично, равенство нулю возмущающей силы означает, что равны нулю H и h.

В таком случае уравнение (135) принимает вид

Этому уравнению придадим более удобный вид, для чего выразим, постоянные интегрирования C₁ и C₂ через две другие постоянные величины А и β, однозначно связанные с C₁ и C₂ соотношениями

x = A sin (kt+ β). (140)

Это уравнение является одним из важнейших уравнений в теории колебаний и описывает наиболее простое колебательное движение, называемое гармоническим. Еще в древности было известно, что если некоторая точка M’ (рис. 163) равномерно движется по окружности радиуса О’М’ — А со скоростью kA, то проекция M этой точки на какую-либо ось Ох, лежащую в плоскости окружности, совершает гармонические колебания. Мы воспользуемся рис. 163, чтобы нагляднее ознакомить читателя с параметрами гармонического колебания.

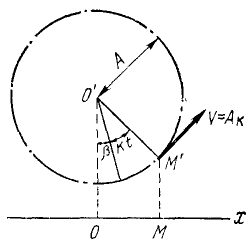
Рис. 163

Если точка M’ опишет полную окружность, то точка M’ совершит одно полное колебание.

Время одного полного колебания точки M (или, что то же, время,в течение которого точка M’ описывает одну полную окружность) называют периодом -τ₀ колебаний.

Угловая скорость k, с которой поворачивается радиус-вектор 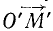при равномерном движении точки M’, равна циклической, круговой или угловой частоте колебаний точки М. Эту величину обычно коротко называют частотой, хотя, как будет видно из дальнейшего, оба понятия не вполне идентичны.

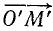
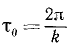
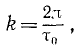
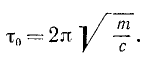
Период и угловая частота связаны простым соотношением, которое становится очевидным, если учесть, что τ₀—это время, в течение которого , вращаясь с угловой скоростью k, поворачивается на 2π:

и (141)

(142)

Период имеет размерность времени

Частота имеет размерность угловой скорости

Из (141) видно, что круговая частота k равна числу полных колебаний, совершаемых в 2π сек. Частота ν колебаний пропорциональна круговой (циклической, угловой) частоте k и равна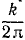. В технике и в физике частоту обычно измеряют в герцах (гц). 1 гц — частота, равная одному полному колебанию (циклу) в секунду. Иначе говоря, герц есть частота такого периодического процесса, который повторяется каждую секунду. Обратите внимание на то, что частота и период гармонических колебаний зависят от массы точки и коэффициента с восстанавливающей силы и не зависят от начальных данных.

Максимальное отклонение А точки M от среднего (равновесного) положения О в ту или в другую сторону (или, что то же, радиус круговой траектории точки М’) называют амплитудой. Амплитуду измеряют в единицах длины:

Аргумент синуса (kt + β) называют фазой колебания, a β—начальной фазой. Физический смысл фазы колебания выявляется при сравнении двух колебаний с одинаковыми частотами, но с разными начальными фазами. Колебание с фазой (kt+ β) опережает колебание с фазой kt, а колебание с фазой (kt — β) отстает от него (разумеется, при положительном β).

Напомним, что А и β являются постоянными интеграции, а следовательно, их определяют по начальным данным. Пусть в начальное мгновение t = 0, x=x₀ и x=x₀. Продифференцировав (140) по времени, получим х = Ak cos (kt + β), и подставляя начальные значения:

(143)

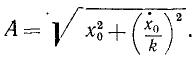
Из тех же равенств можно определить и начальную фазу 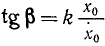. Амплитуда и начальная фаза зависят от частоты и от начальных данных.

Задача №1

Груз весом 2 T подвешен на тросе (рис. 164). При равномерном спуске груза со скоростью υ = 5м/сек произошла неожиданная задержка верхнего конца троса вследствие защемления троса в обойме блока. Пренебрегая весом троса, определить его наибольшее натяжение при последующих колебаниях груза, если коэффициент жесткости троса с = 4 T/см.

Решение. Примем следующие единицы измерений: длина—в см, время — в сек, сила—в Т. Рассмотрим движение груза. На груз действуют две силы: вертикально вниз вес груза 2T, вертикально вверх — натяжение троса. Груз спускался равномерно, следовательно, до защемления натяжение троса равнялось весу груза. В этом равновесном положении его застала авария. После защемления троса груз не остановился мгновенно. В это мгновение он имел скорость 5 м/сек и продолжал опускаться. Но по мере опускания груза сила натяжения троса возрастала от своего начального значения 2T. Ускорение груза направлено по силе и пропорционально ей. Поэтому опускание груза было замедленным и в некоторое мгновение скорость груза, перейдя через нуль, стала направленной вверх, в направлении силы и ускорения. Движение вверх было ускоренным, но по мере того как груз поднимался, растяжение троса, а следовательно, и его натяжение уменьшались, а потому уменьшалось ускорение груза, скорость же продолжала увеличиваться до момента прохождения через равновесное положение. После этого груз, набрав скорость, продолжал подниматься, ио замедленно, так как натяжение троса стало меньше силы веса и равнодействующая приложенных к грузу сил была направлена вниз. Затем скорость стала равной нулю, груз начал падать вниз, натяжение троса возрастало и движение повторялось снова неопределенное количество раз.

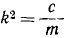
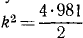
Начало О системы отсчета выберем обязательно в равновесном положении груза, относительно которого происходят колебания, направив ось Ox вертикально вниз (рис. 164). В начальное мгновение (в момент защемления троса) было: x₀= 0; x₀= 500 см/сек. Квадрат круговой частоты определим по (134). После подстановки в формулу имеем . Определим амплитуду по формуле (143):

Таким образом, при равновесном положении груза натяжение троса равно 2T; когда же груз опустился на одну амплитуду, то трос растянулся еще на 11,28 см, а при жесткости троса в 4 T/см натяжение его увеличилось еще на 45,12 Т.

Натуральный логарифм отношения двух последующих амплитуд затухающих колебаний называют логарифмическим декрементом

Свободные колебания с сопротивлением

Движение под действием восстанавливающей силы и силы сопротивления будем называть свободными колебаниями. Мы только что убедились, что свободные колебания без сопротивления являются гармоническими и, раз возникнув, они повторялись бы до тех пор, пока их не прекратила бы или не изменила бы какая-нибудь внешняя сила. Пусть возмущающая сила отсутствует (P = 0, H = 0, h = 0), а на точку действуют силы F=-cx и R =—ах. Дифференциальное уравнение (135) движения точки M принимает вид

х + 2nx 4- k 2 x = 0, (144)

а его интеграл получим, положив в (138) h=0:

или, если воспользуемся соотношениями (140),

(145)

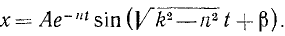
Постоянные А и β определяют по начальным данным.

Наиболее существенное отличие уравнения (145) от уравнения (140), иначе говоря, наиболее существенное изменение в свободном колебании точки М, внесенное наличием силы сопротивления, заключается в множителе e -nt , который с течением времени непрерывно уменьшается, вследствие чего амплитуда Ae -nt колебаний с сопротивлением убывает по экспоненциальному закону, асимптотически приближаясь к нулю. Такое колебание называют затухающим.

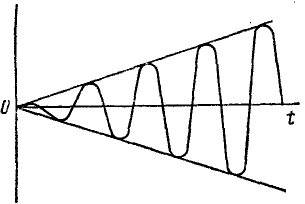
Переходя к определению периода затухающих колебаний, обратим внимание на то, что вообще периодом периодического движения называют промежуток времени между двумя последовательными прохождениями точки (или системы) через одно и то же положение водном и том же направлении. В случае затухающих колебаний только равновесное положение удовлетворяет такому определению периода, через всякое же другое положение точка M (или любая система, совершающая затухающие колебания) проходит через неравные промежутки времени (см. рис. 165). Поэтому под периодом затухающих колебаний понимают промежуток времени τ₁ между двумя последовательными прохождениями точки M (или системы) через положение равновесия в одинаковом направлении. В таком же смысле колебания, описываемые уравнением (145), могут быть названы изохронными. Период затухающих колебаний можно определить но формуле

(146)

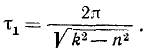
Проф. И. М. Бабаков в учебнике «Теория колебаний» рекомендует для практических расчетов более удобную формулу:

(146 / )

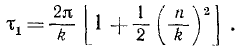
Сравнивая (141) и (146), мы видим, что сопротивление увеличивает период свободных колебаний, но незначительно.

Гораздо больше оно влияет на убывание амплитуд. Так, например, при n = 0,05 k сопротивления увеличивают период на 0,125%, а амплитуда за время одного полного колебания уменьшается более чем на 25%. На рис. 165 изображен график затухающих колебаний для случая n = 0,05 k, позаимствованный из «Лекций» проф. Е. Л. Николаи.

Отношение абсолютных значений двух последовательных амплитудных отклонений точки от равновесного положения называют коэффициентом затухания:

(147)

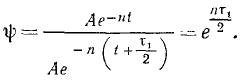
Для характеристики быстроты убывания амплитуды удобнее пользоваться натуральным логарифмом коэффициента затухания, называемым логарифмическим декрементом колебаний:

(147 / )

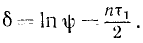
На рис. 165 пунктиром изображены кривые, уравнения которых x= Ае -n и х = —Ae -nt . График затухающих колебаний расположен между этими двумя кривыми и поочередно их касается.

Задача №2

Маятник, масса которого равна 1 кг и период качания в безвоздушной среде τ₀=l сек, заставили качаться вереде, сопротивляющейся но закону R =—2х н. Определить: 1) период затухающих колебаний маятника и 2) уменьшение амплитуды в течение трех периодов.

Решение. Определим параметры колебаний.

Круговая частота. Период τ₀=l сек= 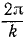, откуда k=2π = G,28.

Коэффициент α=2; m=1; 2n=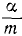, откуда n=l.

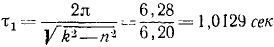
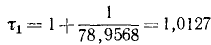
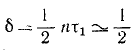
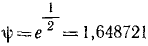
Период затухающих колебаний , или по (146′),
. Логарифмический декремент . Коэффициент затухания .

Отношение каждого максимального отклонения к последующему (через полпериода) равно коэффициенту затухания, следовательно, если амплитуду при первом размахе принять за 1, то следующие уменьшаются в отношении .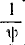

Под действием восстанавливающей и возмущающей сил точка совершает сложное колебание, являющееся результатом наложения трех гармонических колебаний: свободного, сопровождающего свободного и вынужденного

Вынужденные колебания без сопротивления

Пусть на точку М, движущуюся по оси Ох, действуют две силы — восстанавливающая F=— CX и возмущающая P =H sin pt, направленные также по оси Ох. Величина pt может быть названа фазой силы, постоянную р назовем круговой частотой возмущающей силы, а период этих изменений обозначим через τ. Действие сопротивления мы пока не учитываем, поэтому, положив в уравнении (135) n = 0, получим следующее дифференциальное уравнение вынужденных колебаний без сопротивления:

x+ k 2 x = h sin pt. (148)

Чтобы найти решение этого уравнения, надо в (138) положить равным нулю не только n, но и δ, так как согласно (137) δ = 0 при n = 0. Имеем

Определим постоянные. Если в начальное мгновение х = x₀ и x = χ₀, то

(149)

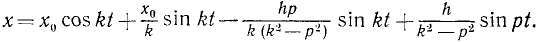
Первые два слагаемых описывают свободные колебания с частотой k. Воспользовавшись соотношениями (140″), эти два слагаемых можно представить в виде x₁ = A sin (kt + β). Если в начальное мгновение х = х= 0, то эти колебания во все время действия возмущающей силы не возникают. Третье слагаемое

— гармоническое колебание, происходящее с частотой k свободных колебаний, но с амплитудой, зависящей от возмущающей силы. Это колебание всегда, при любых начальных условиях, сопровождает вынужденные колебания и его называют свободным сопровождающим колебанием. Четвертое слагаемое

(149 / )

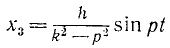
описывает вынужденные колебания. Таким образом, колебания точки являются результатом линейного наложения трех гармонических колебаний: 1) свободных, 2) сопровождающих свободных и 3) вынужденных (рис. 166):

(149 // )

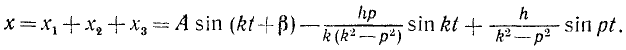
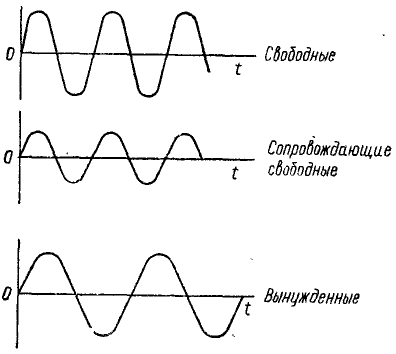
Рис. 166

На схеме (рис. 166) приведены только частоты этих колебаний, но разумеется, не изображены амплитуды и начальные фазы.

Вынужденные колебания происходят с частотой р, равной частоте возмущающей силы. Они не зависят от начальных данных.

Как видно из (143), для изменения амплитуды свободных колебаний достаточно изменить начальное отклонение или начальную скорость. Напротив, для изменения амплитуды вынужденных колебаний надо изменить возмущающую силу, что обычно бывает сопряжено с необходимостью преобразования конструкции.

Если частота р вынужденных колебаний меньше частоты k собственных (случай «малой» частоты), то амплитуда вынужденных колебаний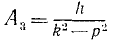, а фаза pt вынужденных колебаний совпадет
с фазой pt возмущающей силы. По если р > k (случай «большой» частоты), то выражение, написанное для А₃, становится отрицательным, однако амплитуда не может быть отрицательной. Это кажущееся несоответствие объясняется тем, что при р > k фаза вынужденных колебаний противоположна фазе возмущающей силы и уравнение вынужденных колебаний имеет вид

Резонанс

Если частоты собственных и вынужденных колебаний близки между собой, то амплитуды получаются очень большими. Напомним, что при интегрировании уравнения (135) мы положили p≠k. Если р= k, то дифференциальное уравнение (148) имеет вид

x-k 2 x = h sin kt (148′)

Будем искать частное решение вида

Определив х =— 2Bk sin kt— Btk 2 cos kt и подставив его вместе с х в дифференциальное уравнение, получим
— 2Bk sin kt = h sin kt,

Находим общее решение дифференциального уравнения движения:

Дифференцируем по времени:

Если в начальное мгновение x=x₀ и x=x₀, то

и общее решение принимает вид

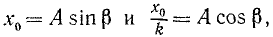
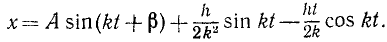
или, полагая получим

(148»’)

Следовательно, и при равенстве частот движение точки состоит из трех колебательных движений, однако вынужденные колебания представлены непериодическим членом, в коэффициент которого входит множителем время. C течением времени это третье слагаемое, называемое вековым членом, безгранично растет по абсолютной величине. Размах вынужденных колебаний непрерывно растет по линейному закону. Это явление называется резонансом. График вынужденных колебаний при резонансе представлен на рис. 167.

Задача №3

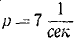
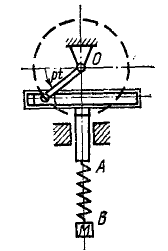
Груз M подвешен в точке В к пружине AB (рис. 168), верхний конец А которой прикреплен к поступательно движущейся кулисе. Кривошип кулисного механизма имеет длину а = 0,02 м и вращается с угловой скоростью , вследствие чего точка А совершает гармонические колебания по закону х_А =0,02 sin 7t м. Определить вынужденные колебания груза М, если его вес G = 3,6 н, а жесткость пружины с = 36 н/м.

Рис. 168

Решение. Составим дифференциальное уравнение движения груза М. Начало координат выберем в точке, с которой центр тяжести груза совладал в момент начала движения (при t = 0), когда верхний конец А пружины, совершающей гармонические колебания вместе с кулисой, занимал свое среднее положение. При сделанном нами выборе начала отсчета (в равновесном положении груза) вес G = 3,6 н уравновешивался статическим натяжением пружины с λ_cr = 36 ∙ 0,1. Наличие этих двух взаимно уравновешенных сил эквивалентно их отсутствию, а потому мы можем их отбросить и в дальнейшем рассматривать движение центра тяжести груза лишь под действием натяжения пружины, обусловленного только ее динамической деформацией, т. е. только деформацией пружины при колебании груза около равновесного положения.

При t ≠ 0 положение центра тяжести груза определяется координатой х, получающейся от суммирования двух перемещений: динамической деформации пружины и перемещения a sin pt верхнего конца А пружины. Следовательно, динамическая деформация пружины равна разности перемещений ее нижнего конца В и верхнего конца А, т. е. равна х—α sin pt . Дифференциальное уравнение движения центра груза имеет вид

mx = — с (х—a sin pt).

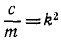
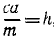
Деля обе части уравнения на m и вводя обозначения и , придадим этому уравнению знакомый нам вид (148)

x + k 2 x = h sin pt,

где

Подставляя в (149′), находим вынужденные колебания груза.
Ответ. 0,04 sin 7t.

Задача №4

Статический прогиб рессор товарного вагона равен 5 см. Определить критическую скорость вагона, при которой начнется «галопирование» вагона, если на стыках рельсов вагон испытывает толчки, вызывающие вынужденные колебания на рессорах: длина рельсов равна 12 м.

Решение. Жесткость рессор 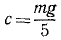, частота собственных колебаний

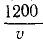
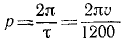
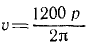
Если поезд идет со скоростью υ см/сек, то вагон получает толчки на стыках через каждые сек. Таков период τ возмущающей силы. Частота возмущающей силы , откуда . Галопирование вагона произойдет при резонансе, т. е. при равенстве частот собственных и вынужденных колебаний. Подставляя в выражение, полученное для скорости, р = k = 14, найдем

Чтобы выразить скорость в км/ч, умножим выраженную в см/ceκ скорость на 0,036.

Если к точке приложены восстанавливающая и возмущающая сила и сила сопротивления, то свободные колебания затухают и остаются только вынужденные

Влияние сопротивления на вынужденные колебания

Если на точку, кроме восстанавливающей и возмущающей сил, действует также и сила R сопротивления, то движение точки описывается дифференциальным уравнением (135) и его решением (138).

Первый член правой части (138) с возрастанием t стремится к нулю, и соответствующие ему колебания точки с течением времени затухают, поэтому ими можно пренебречь. Остаются только вынужденные колебания (рис. 169):

(150)

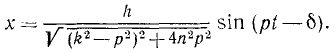
Они происходят с частотой возмущающей силы, сопротивление не влияет на период вынужденных колебаний. Амплитуда не зависит от начальных условий и времени и не изменяется с течением времени.

Предположим, что возмущающая сила сохраняет свое максимальное значение Н. При равновесии под действием такой силы и восстанавливающей силы F =— сх точка M получила бы так называемое статическое отклонение

Из этого соотношения найдем максимальное ускорение точки M под действием возмущающей силы: h=k 2 x_ст и, подставляя это значение h в выражение (150), выразим амплитуду вынужденных колебаний равенством

Отношение частоты вынужденных колебаний к частоте собственных колебаний

(151)

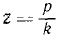
носит название коэффициента расстройки и отношение величины n, измеряемой в ceκ -1 , к частоте собственных колебаний называют безразмерным коэффициентом вязкости:

(151′)

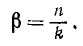
Введя эти обозначения в предыдущее равенство и разделив обе части его на x_ст, получим:

(152)

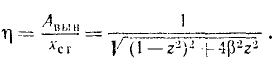
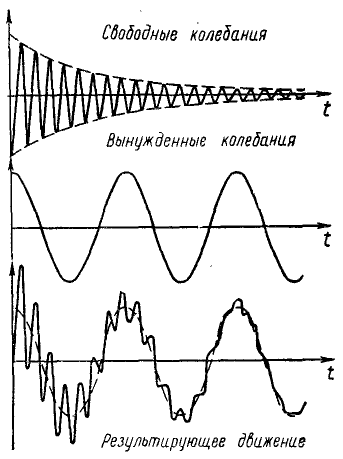
Рис. 169

Величина η—коэффициент динамичности — позволяет охарактеризовать динамический эффект, вызываемый возмущающей силой.

Коэффициент динамичности η зависит от двух величин (z и β).

Задавшись каким-либо значением β, и откладывая по оси абсцисс различные значения z, а по оси ординат—соответствующие значения коэффициента динамичности η, получим, так называемые, резонансные кривые. На рис. 170 изображены резонансные кривые для значений безразмерного коэффициента вязкости: 0,25, 0,15. и 0,10. Пунктиром нанесена уходящая в бесконечность при 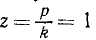резонансная кривая, соответствующая β = 0, т. е. вынужденным колебаниям без сопротивления.

Как показывает график (рис. 170) в областях, достаточно далеких от резонанса, амплитуды вынужденных колебаний с сопротивлением почти не зависят от безразмерного коэффициента вязкости. В этих областях при вычислении амплитуд вынужденных колебаний можно не учитывать сопротивлений и пользоваться более простой формулой

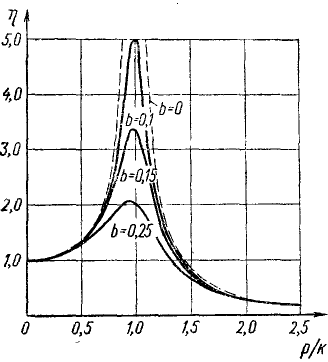
Рис. 170

При резонансе (р = k) амплитуда вынужденных колебаний при наличии сопротивлений остается конечной, но наибольшее значение амплитуда имеет, если 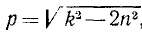, в чем легко убедиться, определив максимум амплитуды при различных р, считая h, k и п данными.

В вынужденных колебаниях с сопротивлением всегда бывает сдвиг фазы колебания по отношению к фазе .возмущающей силы. Величина этого сдвига определяется формулой (137).

Заметим, что все сказанное здесь относительно малых колебаний материальной точки полностью соответствует малым колебаниям материальной системы с одной степенью свободы.

Рекомендую подробно изучить предмет:

Теоретическая механика

Ещё лекции с примерами решения и объяснением:

Количество движения
Момент количества движения
Мощность и работа силы
Потенциальная энергия
Естественный и векторный способы определения движения точки
Координатный способ определения движения точки
Касательное и нормальное ускорения точки
Основные законы динамики

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Механические колебания и волны

Содержание:

Механическая волна представляет собой процесс распространения механических колебаний в упругой среде. Из-за наличия упругих связей между частицами среды периодические смещения одной из частиц вызывают смещение соседних частиц с таким же периодом — этот процесс распространяется в упругой среде с некоторой скоростью, определяемой только модулем упругости и плотностью среды.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Механические колебания и волны

Колебаниями называют движения или изменения состояния, повторяющиеся через определенные промежутки времени.

Физика колебаний и волн — раздел общей физики, изучающий физические явления, характеризующиеся циклическим изменением физических величин во времени и в пространстве. Это — одна большая часть школьного курса физики, изучается после электромагнетизма ( рассматривая механические и электромагнитные процессы вместе ) или сразу с механикой ( в связи с тем, что теория колебаний и волн развивается на основе кинематики и динамики, что охватывает механика ).

Колебательное движение

В природе и технике встречается очень много повторяющихся процессов, в основе которых лежат колебания того или иного вида и создаваемые ими волны.

К такого рода процессам относятся звуковые явления, работа часового механизма, переменный ток в цепи, электромагнитные колебания и т. д.

Природа колебаний разнообразна, но для их описания ввели такие величины, которые оказались одинаково применимыми ко всем колебаниям, независимо от их природы. Проще всего выяснить физический смысл этих величин на примере механических колебаний, которые наиболее наглядны.

На рис. 24.1 показаны тела, совершающие различные механические колебания: 1 — колебания маятника; 2 — колебания жидкости; 3 — колебания пружины с грузом; 4 — колебания струны. На рис. 24.1, а все тела находятся в положении устойчивого равновесия. Для того чтобы вывести эти тела из равновесия, нужно за счет работы какой-нибудь внешней силы сообщить им избыточную энергию. Тогда они займут положения, показанные на рис. 24.1, б. Если теперь предоставить этим телам возможность двигаться беспрепятственно, то они начинают совершать колебательное движение, поочередно проходя положения в, г, д и снова б, а затем повторяют весь цикл движения в том же порядке.

Проследив за движением какой-либо точки одного из этих тел, можно видеть, что она при своем движении проходит одну и ту же траекторию поочередно .в двух противоположных направлениях. Поскольку характер движения всех точек тела одинаков, колебательные процессы удобно изучать на примере колебательного движения одной точки тела. Подчеркнем, что важнейшим признаком колебательного движения является его повторяемость через равные промежутки времени Т, т. е. его периодичность.

Таким образом, механическим колебанием называют периодически повторяющееся движение материальной точки по какой-либо траектории, которую эта точка проходит поочередно в противоположных направлениях. Отметим, что каждую определенную точку траектории колеблющаяся частица проходит, имея одинаковую по величине скорость.

Полным колебанием точки называют один законченный цикл колебательного движения, после которого оно повторяется в том же порядке.

Условия возникновения колебаний

Выясним, при соблюдении каких условий возникает и поддерживается в течение некоторого времени колебательное движение.

Первым условием, необходимым для возникновения колебаний, является наличие у материальной точки избыточной энергии (кинетической или потенциальной) по сравнению с ее энергией в положении устойчивого равновесия (§24.1).

Второе условие можно установить, проследив за движением груза 3 на рис. 24.1. В положении б на груз 3 действует сила упругости F₁, направленная к положению равновесия груза (см. рис. 24.1, б). Под действием этой силы груз смещается к положению равновесия с постепенно возрастающей скоростью движения и, а сила F₁ уменьшается и исчезает, когда груз попадает в это положение (рис. 24.1, в). Скорость груза в этот момент максимальна по величине, и груз, проскакивая через положение равновесия, продолжает двигаться вправо. При этом возникает сила упругости F₂, которая тормозит движение груза 3 и останавливает его (рис. 24.1, г). Сила F₂ в этом положении имеет максимальную величину; под действием этой силы груз 3 начинает двигаться влево. В положении равновесия (рис. 24.1, д) сила F₂ исчезает, а скорость груза достигает наибольшего значения, поэтому груз продолжает двигаться влево, пока не займет положение б на рис. 24.1. Далее весь описанный процесс повторяется снова в том же порядке.

Таким образом, колебания груза 3 происходят вследствие действия силы F и наличия у груза инерции. Силу, приложенную к материальной точке, всегда направленную к положению устойчивого равновесия точки, называют возвращающей силой. В положении устойчивого равновесия возвращающая сила равна нулю и возрастает по мере удаления точки от этого положения.

Итак, вторым условием, необходимым для возникновения и Продолжения колебаний материальной точки, является действие на материальную точку возвращающей силы. Напомним, что эта сила всегда возникает, когда какое-либо тело выводится из положения устойчивого равновесия.

В идеальном случае, при отсутствии трения и сопротивления среды, полная механическая энергия колеблющейся точки остается постоянной, так как в процессе таких колебаний происходит лишь переход кинетической энергии в потенциальную и обратно. Такое колебание должно продолжаться неопределенно долгое время.

Если колебания материальной точки происходят при наличии трения и сопротивления среды, то полная механическая энергия материальной точки постепенно убывает, размах колебаний уменьшается и через некоторое время точка останавливается в положении устойчивого равновесия.

Бывают случаи, когда потери энергии материальной точкой настолько велики, что если внешняя сила отклоняет эту точку из положения равновесия, то она теряет всю свою избыточную энергию при возвращении в положение равновесия. В этом случае колебаний не получится. Итак, третье условие, необходимое для возникновения и продолжения колебаний, следующее: избыточная энергия, полученная материальной точкой при смещении из положения устойчивого равновесии, не должна полностью расходоваться на преодоление сопротивления при возвращении в это положение.

Классификация колебательных движений тела в зависимости от действующей на него силы

В предыдущем параграфе было выяснено, что на колеблющуюся точку обязательно действует возвращающая сила. Колебания, которые совершает материальная точка (тело) под действием только одной возвращающей силы, называют собственными колебаниями точки (тела).

Отметим, что собственные колебания тела на практике никогда не происходят, так как на колеблющееся тело всегда действует еще сила сопротивления среды (сила трения). Действие силы сопротивления на колеблющееся тело сводится к тому, что несколько замедляется весь процесс колебания, т. е. увеличивается время одного полного колебания и постепенно уменьшается размах колебаний. Колебания материальной точки, которые происходят при действии на нее силы сопротивления среды и возвращающей силы, называют свободными колебаниями.

Свободные колебания тела тем меньше отличаются от его собственных колебаний, чем меньше сила сопротивления среды, в которой происходят эти колебания. Таким образом, собственные колебания можно считать предельным случаем свободных колебаний при неограниченном уменьшении силы сопротивления.

Рассмотрим еще один вид колебаний. Когда на полу стоит ритмично работающая машина, например электродвигатель, то пол колеблется. При работе двигателя на катере, на самолете их корпуса тоже колеблются. Эти колебания, вызываются периодически повторяющимся внешним воздействием. Колебания тела, которые создаются периодически действующей на тело внешней силой, называют вынужденными колебаниями. В этом случае на колеблющееся тело кроме периодически изменяющейся внешней силы действует еще сила сопротивления и возвращающая сила.

Параметры колебательного движения

Существуют характерные количественные признаки колебательного движения, которые позволяют отличить его от других колебаний и при известных условиях сохраняют свои числовые значения. Их называют параметрами колебательного движения.

Первым таким признаком колебательного движения является его периодичность. Величину Т, характеризующую периодичность колебательного движения, называют периодом колебания. Период колебания измеряют временем, затраченным на одно полное колебание, и выражают в секундах.

Другим характерным признаком колебания является его частота (быстрота повторяемости), обозначаемая (греч. «ню»). Величину характеризующую скорость повторяемости колебательного движения, называют частотой колебаний. Частоту колебаний шла измеряют числом полных колебаний за единицу времени:

(24.1)

(Покажите, что частота выражается формулой (24.1).)

Выведем единицу частоты:

За единицу частоты колебаний принимают герц (Гц). Герцем называют такую частоту колебаний тела, при которой оно совершает одно полное колебание за одну секунду.

Третьим характерным признаком колебательного движения является его амплитуда. Амплитудой А называется величина максимального отклонения колеблющейся точки от положения ее устойчивого равновесия. На рис. 24.2 амплитуда колебания точки О равна OB.

Итак, у колебательного движения точки имеется три параметра: период Т, частота и амплитуда А. Поскольку величины Т и связаны формулой (24.1), для описания колебательного движения можно пользоваться любой из них (Т или ) и амплитудой А.

Колебания точки, которые происходят с постоянной амплитудой, называют незатухающими, а колебания с постепенно уменьшающейся амплитудой — затухающими. Вспомним, что затухающими колебаниями являются свободные колебания. Следует иметь в виду, что незатухающие колебания могут быть не только собственными. Вынужденные колебания тоже происходят с постоянной амплитудой. Поскольку сопротивление среды вызывает превращение механической энергии во внутреннюю, энергия колеблющейся точки при каждом колебании должна пополняться за счет работы периодически меняющейся внешней силы. Примером таких колебаний служат незатухающие колебания маятнику в часах, где энергия маятника пополняется за счет энергии сжатой пружины. Отметим, что период вынужденных колебаний всегда совпадает с периодом изменения вынуждающей силы.

Энергия колебательного движения определяется его параметрами и массой колеблющегося тела. В теории колебаний доказывается, что избыточная энергия колеблющейся материальной точки прямо пропорциональна ее массе, квадрату амплитуды и квадрату частоты колебаний.

Величины, характеризующие мгновенное состояние колеблющейся точки

Период, частота и амплитуда колебательного движения не дают никаких сведений о том, где находится колеблющаяся точка в данный момент времени и в каком направлении она движется. Поэтому нужно ввести еще величины, характеризующие мгновенное состояние колеблющейся точки.

Первой такой величиной является смещение точки. Величину характеризующую положение колеблющейся точки в выбранный момент времени относительно положения равновесия, называют смещением. Смещение измеряют расстоянием от положения устойчивого равновесия колеблющейся точки до ее положения в заданный момент времени. Чтобы числовое значение смещения было однозначным, ему приписывают знак. Например, если смещение груза 3 из положения равновесия вправо на рис. 24.1 считать положительным, то его смещение влево будет отрицательным.

Нетрудно сообразить, что амплитуда А численно равна наибольшему смещению колеблющейся точки от ее положения равновесия

(24.2)

Второй важной величиной, характеризующей мгновенное состояние колеблющейся точки, является фаза. Величину характеризующую как положение, так и направление движения колеблющейся точки в заданный момент времени, называют фазой колебания. Фазу колебания точки измеряют отвлеченным числом, показывающим, какая часть периода прошла от момента начала колебания точки.

Хотя фаза может иметь и большое числовое значение, обычно ее выражают правильной дробью, отбрасывая целые периоды, которые прошли от момента начала колебания, так как по прошествии целого периода весь процесс повторяется снова в том же порядке.

Чтобы значение фазы было однозначным, нужно оговорить, какое положение колеблющейся точки берется за начало отсчета фазы. Например, можно принять за начало отсчета фазы колебания маятника положение равновесия маятника при его движении влево (рис. 24.3). Тогда изменения фазы в процессе колебания маятника будут выражаться числами, указанными на рис. 24.3. Если о таком маятнике нам скажут, что его фаза равна 1/2, то мы будем знать, что он находится в положении равновесия и движется вправо.

Заметим, что от смещения фаза отличается не только тем, что позволяет определить направление движения. Смещение колеблющейся точки связано с амплитудой колебаний, а фаза — нет. (Подумайте, могут ли два одинаковых маятника иметь при колебаниях
происходящих с одинаковыми периодами и амплитудами. На рис. 24.4, а изображены два одинаковых маятника, которые одновременно начинают колебания из положений, показанных на рисунке. Тогда их периоды и амплитуды будут одинаковы, но направления движений окажутся противоположными. Приняв для обоих маятников одинаковые начальные условия для отсчета фазы, различие в,их колебаниях можно выразить разностью фаз. Представим себе, что оба маятника удерживаются в крайнем левом положении. Если правый маятник отпустить и, когда он займет крайнее; правое положение, отпустить левый, то они оба будут колебаться, как показано на рис. 24.4, а. Поскольку левый маятник начал свои колебания на полпериода позже правого, то говорят, что правый маятник опережает левый по фазе на 1/2. (Подумайте, почему можно сказать, что правый маятник отстает по фазе от левого на 1/2.) Итак, колебания маятников на рис. 24.4, а происходят с разностью фаз 1/2, а на рис. 24.4, б — с разностью фаз 0 или 1.

Важно отметить, что когда два колебания происходят с одинаковым периодом (частотой), то разность фаз между ними сохраняется неизменной в течение всего времени колебаний. Сказанное ниже относится к таким колебаниям.

Если колебания двух точек происходят с разностью фаз 0 или 1, то говорят, что они колеблются (находятся) в одинаковой фазе. В частности, когда колеблющиеся точки все время движутся в одном направлении, то их фазы одинаковы. Такие колебания иногда называют синхронными.

Когда колебания двух точек происходят с разностью фаз 1/2, то говорят, «по они имеют противоположные фазы. В частности, когда колеблющиеся точки все время движутся в противоположных направлениях, их фазы колебаний противоположны.

Кроме смещения и фазы, мгновенное состояние колеблющейся точки характеризуют скоростью ее движения и ускорением так как эти величины непрерывно изменяются со временем. Скорость имеет максимальное значение в положении равновесия точки, а в крайних положениях она равна нулю. Ускорение равно нулю в положении равновесия и имеет максимальное значение в крайних положениях колебания точки (объясните, почему).

Гармоническое колебание

В тех случаях, когда возвращающей силой является равнодействующая силы упругости и силы тяжести, параметры колебательного движения можно связать с параметрами движения точки по окружности.

Чтобы найти эту связь, проделаем следующий опыт. Поставим перед экраном центробежную машину, а на ее диске поместим стержень с шариком Ш на конце (рис. 24.5). Направим свет так, чтобы на экране получилась резкая тень Т от шарика Ш. Поместим между экраном и машиной маятник М так, чтобы его тень совпала с тенью шарика на экране. Если заставить маятник качаться в плоскости, параллельной экрану, то можно вращать диск с такой постоянной скоростью, что тени шарика Ш и маятника М на экране будут всё время совпадать. Это доказывает, что проекция шарика на экране совершает точно такое же колебательное движение, как и маятник М.

Таким образом, если точка совершает колебание с постоянными амплитудой А и периодом Т, то такое же. колебание совершает проекция точки, равномерно движущейся по окружности с радиусом А и периодом Т, на один из диаметров окружности. Это дает возможность изучать особенности колебаний с помощью движения проекции указанной выше точки по диаметру окружности.

Допустим, что точка С на рис. 24.6 равномерно движется по окружности радиуса O’С=А с угловой скоростью и совершает полный оборот за время Т. Тогда проекция точки С на прямую MN будет совершать колебания с амплитудой А и периодом Т. Отсчет времени будем вести от того момента, когда подвижный радиус занимает положение O’С, а колеблющаяся точка — положение O». Пусть за время t радиус повернулся на угол тогда проекция его конца С переместится по прямой МN на расстояние На окружности точками показаны положения конца подвижного радиуса через равные промежутки времени,-а на прямой MN — положения колеблющейся точки в те же моменты времени.

Смещение колеблющейся точки В от положения равновесия можно найти из треугольника O’C₁D:

(24.3)

(24.3а)

В этих формулах называют фазовым углом или фазой и выражают в радианах. Величину в применении к колебательному движению называют круговой или циклической частотой. Поскольку при равномерном движении точки по окружности угловая скорость выражается формулами

или (24.4)

то для фазового угла получаем формулы

или (24.5)

Из этих формул видно, что числовое значение фазы в радианах отличается от ее значения в долях периода только постоянным множителем

Отсчет времени можно производить от любого момента времени, например от момента положения точки С на рис. 24.7. В этом случае начальное положение этой, точки определяют углом который называют начальной фазой. Тогда фазу колебания можно выразить следующими формулами:

(24.6)

или (24.6а)

Колебания, которые описывают формулой (24.3), часто называют синусоидальными (или косинусоидальными). В физике такие колебания, при которых смещение подчиняется синусоидальному закону, называют гармоническими. В частности, колебания, которые происходят под действием только одной возвращающей силы, пропорциональной смещению, являются гармоническими. Следовательно, когда возвращающая сила выражается формулой

(24.7)

а другие силы на точку не действуют, ее колебания будут гармоническими. (Знак минус означает, что и напряжены противоположно.)

Докажем это на примере собственных колебаний груза на пружине (рис. 24.8). Направим ось координат X по линии смещения груза, а за начало координат возьмем положение равновесия груза — точку О. Тогда координата будет совпадать со смещением груза и с абсолютной деформацией пружины.

Поскольку сила упругости пружины пропорциональна ее абсолютной деформации (см. выражение (11.7а) в § 11.8), то возвращающая сила F_B соответствует формуле (24.7). Если не учитывать трение, то сила F_B будет равнодействующей сил, действующих на груз, и в соответствии с вторым законом Ньютона

или (24.8)

где — масса груза.

При движении вдоль оси скорость является производной координаты по времени а ускорение — производной скорости по времени, т. е. второй производной координаты по времени Поэтому уравнение (24.8) можно записать в виде

(24.9)

Из курса математики известно, что вторая производная синуса и косинуса пропорциональна самой функции, взятой с обратным знаком. Поэтому решение уравнения (24.9) следует искать в виде (24.3а): Первая производная координаты по времени будет равна а вторая производная Подставим и в (24.9):

Отсюда, и

(24.10)

Таким образом, функция (24.3а) действительно является решением уравнения (24.9), т. е. собственные колебания под действием возвращающей силы вида (24.7) являются гармоническими, а их круговая частота со определяется выражением (24.10).

Уравнение гармонического колебания и его график

Формулу, выражающую зависимость смещения колеблющейся точки от времени, называют уравнением колебательного движения. Таким образом, формулу (24.3) можно назвать уравнением гармонического колебания. Более общее уравнение гармонического колебания можно получить, заменив в (24.3) его значением из формул (24.6) и (24.6а):

(24.11)

или (24.11а)

Колебание с начальной фазой подчиняется косинусоидальному закону: Это колебание, конечно, является гармоническим.

График гармонического колебания представляет собой синусоиду, которую строят следующим образом. Возьмем на продолжении прямой О’O» и точку О (рис. 24.6) и примем ее за начало координат. По оси абсцисс будем откладывать время t, а по оси ординат — смещение Указав на оси абсцисс точки и т. д., покажем соответствующие им смещения точками и т. д.

Соединив точки В’ плавной кривой, получим график гармонического колебания точки. На рис. 24.6 показан график для одного периода Т. За каждый следующий период колебания будет добавляться еще такой же отрезок графика.

На рис. 24.9 показаны графики двух гармонических колебаний с одинаковыми периодами и амплитудами, но g разностью фаз Колебание, график которого расположен левее (синусоида A), опережает по фазе второе колебание (синусоида В) на Из рис. 24.9 видно, что подвижный радиус OA’ опережает на подвижный радиус ОВ’ второго колебания.

При затухающих колебаниях период остается постоянным, а амплитуда постоянно уменьшается. График затухающего колебания показан на рис. 24.10. Итак, при свободных колебаниях полной повторяемости процесса колебания нет и считать их гармоническими можно только с некоторым приближением.

Математический маятник

Наблюдая за колебаниями маятников разной длины, легко заметить, что периоды их колебаний связаны с длиной маятников. Однако в случае реальных маятников не ясно, что следует считать длиной маятника. Например, перемещая диск маятника стенных часов вверх или вниз по стержню, можно изменять период его колебаний, хотя длина стержня маятника остается неизменной. Чтобы обойти эту трудность, сначала рассмотрим особенности колебания математического маятника, для которого вопрос о его длине ясен.

Математическим маятником называют материальную точку, подвешенную на невесомой и нерастяжимой нити. Маленький тяжелый шарик, например свинцовый, подвешенный на тонкой, длинной и нерастяжимой нити, является хорошей моделью математического маятника, на которой и изучают его свойства. Прежде всего выясним, можно ли считать колебания математического маятника гармоническими. Для этого надо установить, как связана возвращающая сила F_в со смещением

Пусть колеблющийся математический маятник (рис. 24.11) длиной l занимает мгновенное положение ОМ₁. Возвращающая сила F_в равна равнодействующей силы тяжести F_ти силы упругости нити F_н и направлена по касательной к дуге M₁M₀ (если пренебречь центростремительной силой, необходимой для движения маятника по дуге). Из подобия треугольника, образованного силами F_т и F_в, и имеем откуда

К положению равновесия маятник движется по дуге M₁M₀, поэтому смещение равно длине дуги M₁M₀. Для малых углов длина дуги M₁M₂ приблизительно равна хорде M₁M₂, а длина дуги M₁M₀ — половине хорды M₁M₂, т. е. или . Поэтому для малых углов а можно считать, что

(24.12)

Знак минус поставлен потому, что и F_B всегда направлены противоположно друг другу.

Величины m, g и l при колебаниях маятника в заданном месте Земли постоянны. Поэтому из (24.12) видно, что возвращающая сила F_B прямо пропорциональна смещению, т. е. выражается формулой (24.7): где Напомним, что это верно, когда угол достаточно мал. Отметим, что если — наибольший угол отклонения маятника от положения равновесия, то угол называют углом размаха.

Таким образом, при малом угле размаха (не превышающем нескольких градусов) колебания математического маятника можно считать гармоническими.

Законы колебания математического маятника. Формула маятника

Выясним теперь, чем определяется период колебаний математического маятника. С помощью опыта на модели математического маятника легко установить, что его колебания являются затухающими. Опыт показал, что период колебаний маятника при затуханиях не изменяется, т. е. он не зависит от амплитуды (при небольших углах размаха). Это свойство маятника было открыто Г. Галилеем и носит название изохронности (равновременности). Опыт показывает, что период колебаний маятника не зависит от его массы.

С помощью формулы (24.12) покажем, что период колебаний маятника зависит от его длины l. Поскольку при увеличении l возвращающая сила F уменьшается, то уменьшается и ускорение движения маятника, а следовательно, период его колебаний возрастает. Из той же формулы видно, что при увеличении g растет F_B, а значит, период уменьшается.

Описанные свойства математического маятника формулируют в виде двух законов.

1. При малых углах размаха период колебаний математического маятника не зависит ни от амплитуды, ни от массы маятника.

2. Период колебаний математического маятника прямо пропорционален корню квадратному из длины маятника l и обратно пропорционален корню квадратному из ускорения свободного падения g:

(24.13)

Формулу (24.13) можно получить из (24.10) и (24.4), учитывая, что для математического маятника (§ 24.8).

Заметим, что половину полного колебания называют простым колебанием, например, движение маятника от одного крайнего положения до другого. Так как период простого колебания то формула для вычисления периода Простого колебания математического маятника имеет вид

(24.14)

Физический маятник

Законы колебания математического маятника можно применять только к колебаниям таких тел, размеры которых малы по сравнению с расстоянием от точки подвеса до центра тяжести. Все маятники, для которых это условие не выполняется, называют физическими. Пример такого маятника показан на рис. 24.12.

Колебание физического маятника можно представить себе как совместное колебание множества материальных точек, связанных между собой, т. е. множества математических маятников с разной длиной (два из них показаны на рис. 24.12). Это означает, что применять к физическому маятнику формулу (24.13) нельзя. Действительно, период колебания линейки на рис. 24.12, очевидно, будет больше, чем для математического маятника с длиной l₁ но меньше, чем для математического маятника с длиной l₂.

Чтобы иметь возможность пользоваться формулой (24.13) в случае физического маятника, поступают следующим образом. Приводят физический маятник в колебание и, подсчитав время определенного числа колебаний, находят его период Т, а затем по формуле (24.13) вычисляют длину математического маятника, у которого период тоже равен Т.

Длину математического маятника l_пр, у которого период колебаний равен периоду колебаний физического маятника, называют приведенной длиной этого физического маятника. Таким образом, формулу (24.13) в применении к физическому маятнику надо записывать так!

(24.15)

Отметим, что маятник называют секундным, если период его простого колебания равен одной секунде. Для Москвы приведенная длина такого маятника равна 0,99 м.

Практические применения маятников

Наиболее известным практическим использованием маятника является применение его в часах для измерения времени. Впервые это сделал голландский физик X. Гюйгенс.

Поскольку период колебаний маятника зависит от ускорения свободного падения g, часы, которые идут верно в Москве, будут идти вперед в Ленинграде. Чтобы эти часы шли верно в Ленинграде, приведенную длину их маятника нужно увеличить. (Объясните это с помощью формулы (24.15).)

В геологии маятник применяют для опытного определения числового значения g в разных точках земной поверхности. Для этого по достаточно большому числу колебаний маятника в том месте, где измеряют g, находят период его колебаний Т, a g вычисляют из формулы (24.15):

(24.15а)

Заметное отклонение величины g от нормы для какой-либо местности называют гравитационной аномалией. Определение аномалий помогает находить залежи полезных ископаемых.

Опыт показывает, что качающийся маятник сохраняет плоскость, в которой происходят его колебания. Это означает, что если привести в движение маятник, установленный на диске центробежной машины, а диск заставить вращаться, то плоскость качания маятника относительно комнаты изменяться не будет. Это позволяет с помощью опыта обнаружить вращение Земли вокруг своей оси.

В 1850 г. Ж. Фуко подвесил маятник под куполом высокого здания так, что острие маятника при качании оставляло след на песке, насыпанном на полу. Оказалось, что при каждом качании острие оставляет на песке новый след. Таким образом, опыт Фуко показал, что Земля вращается вокруг своей осн.

Упругие колебания. Превращение энергии при колебательном движении

Колебания, при которых возвращающая сила создается силами упругости, называются упругими.

Примером упругих колебаний может служить колебание пружины с грузом на рис. 24.8. Поскольку сила упругости пропорциональна абсолютной деформации (§§11.7 и 11.8), то сила упругости пружины выражается формулой (24.7): где — смещение груза, закрепленного на пружине, и ее абсолютная деформация, а — жесткость пружины. Следовательно, собственные упругие колебания системы являются гармоническими (см. § 24.6). Можно показать (§ 24.6), что круговая частота упругих колебаний равна

(24.16)

Учитывая (24.4), для периода упругих колебаний получаем

(24.17)

При колебаниях груза на пружине в любом положении груза его полная механическая энергия равна сумме потенциальной энергии (§ 11.8) и кинетической энергии

или (24.18)

где — смещение и — скорость в точке, в которой определяют энергию тела,а — масса груза.

При колебаниях груза наглядно виден переход кинетической энергии груза в потенциальную и обратно. При собственных колебаниях силы сопротивления отсутствуют, поэтому полная механическая энергия колеблющегося тела остается постоянной (§ 6.8). В положении равновесия тело обладает только кинетической энергией, поэтому полную энергию можно выразить формулой

(24.19)

Так как в крайнем положении колеблющееся на пружине тело обладает только потенциальной энергией, то его полную избыточную энергию при колебаниях можно выразить и формулой

(24.20)

где А — амплитуда колебаний. Подставив сюда значение k, найденное из (24.16), получим

(24.21)

т. е. полная энергия колеблющегося тела прямо пропорциональна его массе, квадрату частоты колебаний и квадрату их амплитуды.

Распространение колебательного движения в упругой среде

Когда рыба «клюет» (дергает за крючок), то от поплавка по поверхности воды разбегаются круги. Вместе с поплавком смещаются соприкасающиеся с ним частицы воды, которые вовлекают в движение ближайшие к ним другие частицы и т. д.

Такое же явление происходит с частицами натянутого резинового шнура, если один его конец привести в колебание (рис. 24.13). Распространение колебаний в среде называют волновым движением.

Колеблющееся тело, создающее волновое движение в окружающей среде, называют вибратором. Рассмотрим подробнее, как возникает волна на шнуре.

Если зафиксировать положения шнура через каждые после начала колебаний его первой точки, то получится картина, показанная на рис. 24.14, б—д. Положение а соответствует началу колебаний первой точки шнура. Десять его точек помечены цифрами, а штриховые прямые показывают, где находятся одни и те же точки шнура в разные моменты времени; стрелки показывают направление движения точек в волне.

Через после начала колебания точка 1 занимает крайнее верхнее положение, а точка 2 только начинает свое движение. Поскольку каждая последующая точка шнура начинает свое движение позже предыдущей, то в промежутке 1—2 точки располагаются, как показано на рис. 24.14, б. Еще через точка 1 займет положение равновесия и будет двигаться вниз, а верхнее положение займет точка 2 (положение в). Точка 3 в этот момент только начинает свое движение.

За целый период колебания распространяются до точки 5 шнура (положение д). По окончании периода Т точка 1, двигаясь вверх, начнет свое второе колебание. Одновременно с ней начнет двигаться вверх и точка 5, совершая свое первое колебание. В дальнейшем эти точки будут иметь одинаковые фазы колебаний. Совокупность точек шнура в интервале 1—5 образует волну. Когда точка 1 закончит второе колебание, на шнуре вовлекутся в движение еще точки 5—9, т. е. образуется вторая волна.

Если проследить за положением точек, имеющих одинаковую фазу, то будет видно, что фаза как бы переходит от точки к точке и движется вправо. Действительно, если в положении б фазу 1/4 имеет точка 1, то в положении в эту же фазу имеет точка 2 и т. Д.

Волны, в которых происходит перемещение фазы с определенней скоростью, называют бегущими. При наблюдении за волнами видно именно распространение фазы, например движение гребня волны. Отметим, что все точки среды в волне колеблются около своего положения равновесия и вместе с фазой не перемещаются.

Перенос энергии бегущей волной

При незатухающих колебаниях тела, например маятника, его полная энергия остается неизменной, уменьшение кинетической энергии сопровождается одновременным увеличением его потенциальной энергии, и наоборот. В бегущих волнах дело обстоит иначе.

Распространение бегущих волн связано с передачей энергии от одной колеблющейся точки к другой. Это видно из такого примера. Когда где-либо происходит всплеск воды, например, вызванный прыжком рыбы, то от этого места кругами расходятся волны, которые уносят энергию все дальше от места их возникновения, а поверхность воды, пройденная волнами, успокаивается. Чтобы волны нули непрерывно, частицам воды в том месте, где возникают волны, нужно передавать все новую, энергию. Например, ритмично дергая за поплавок, можно получить непрерывный ряд волн на поверхности воды.

Перенос энергии бегущей волной объясняется тем, что максимум как кинетической, так и потенциальной энергии в такой волне приходится на точку волны, которая проходит положение равновесия. Покажем это на примере волны, бегущей по шнуру.

На рис. 24.15 изображена часть шнура, по которому вправо бежит волна. Здесь следует заметить, что в состоянии покоя этот шнур занимает горизонтальное положение. Таким образом, когда по шнуру бежит волна, то в области точек А и В он не деформирован, а в точке С деформация сдвига у шнура наибольшая.. Поэтому максимум потенциальной энергии упругой деформации шнура приходится на точку С, которая проходит положение устойчивого равновесия.

Но точка С имеет и наибольшую скорость движения по сравнению с другими точками шнура, т. е. обладает максимальной кинетической энергией. Поскольку точка С движется вниз, через мгновение среднее положение займет ближайшая к ней точка справа, к которой перейдет и максимум энергии. Она в свою очередь передаст эту энергию еще дальше и т. д. Таким образом, передача энергии в бегущей волне происходит с той же скоростью, с которой распространяется фаза колебаний. Теория показывает, что энергия, переносимая волной, прямо пропорциональна плотности среды, квадрату амплитуды колебаний и квадрату их частоты (§ 24.12).

Поперечные и продольные волны

Вернемся еще раз к волнам на шнуре, показанным на рис. 24.14, где видно, что волна бежит вправо, а каждая точка шнура движется вверх или вниз около положения равновесия. Волны, в которых колебания частиц среды происходят перпендикулярно к направлению распространения волны, называют поперечными. Они состоят из ряда чередующихся выпуклостей и впадин (рис. 24.16).

Выше говорилось, что у шнура, когда по нему бежит волна, возникает деформация сдвига, следствием которой является изменение формы тела. Поперечные волны возможны только в том случае, когда изменение формы сопровождается появлением-упругих возвращающих сил. Поскольку этим свойством обладают только твердые вещества и поверхность жидкости, поперечные волны могут возникать только в твердых телах и на поверхностях жидкостей (рис. 24.17).

В природе существуют волны и другого вида. Если взять длинную пружину и толкнуть ее вдоль оси, как показано на рис. 24.18, то по ней побегут волны в виде перемещающихся сгущений и разрежений ее витков. В этом примере волна бежит вправо, а каждый виток пружины колеблется вдоль ее оси. Волны, в которых колебания частиц происходят по прямой, вдоль которой распространяется волна, называют продольными. Сдвиг частиц в этой волне происходит по линии, соединяющей их центры, т. е. вызывает изменение объема. Поскольку возвращающие силы при изменении объема возникают не только в твердых телах и жидкостях, но и в газах, продольные волны возможны в твердых телах, жидкостях и газах.

Волна и луч. Длина волны

На рис. 24.17 видно, как распространяются волны на поверхности вода. Светлые окружности изображают гребни волн, т. е. совокупность точек, имеющих максимальное смещение из положения равновесия. Все эти точки колеблются в одинаковой фазе.

Когда волны распространяются не по поверхности среды, а внутри нее, то совокупность точек, колеблющихся В одинаковой фазе, составляет поверхность той или иной формы. Если среда изотропна, т. е. скорость распространения фазы в ней по всем направлениям одинакова, то эта поверхность имеет форму сферы. Такие волны называются сферическими.

Непрерывное геометрическое место точек волны, колеблющихся в одинаковых фазах, называют волновой поверхностью (например, светлые окружности на рис. 24.17). Переднюю волновую поверхность, т. е. наиболее удаленную от источника, создающего волны, называют фронтом волны.

Линию, вдоль которой происходит распространение фронта волны, называют лучом. Нетрудно сообразить, что в изотропной среде луч всегда нормален (перпендикулярен) к волновой поверхности. В изотропной среде все лучи представляют собой прямые линии. Каждая прямая, соединяющая точку, в которой находится источник волны, с любой точкой фронта волны, в этом случае является лучом.

Перемещение фронта волны в такой среде происходит с постоянной скоростью, поэтому за один период колебаний источника, создающего волны, фронт волны перемещается на строго определенное расстояние Поскольку каждая точка в волне совершает вынужденные колебания, частота этих колебаний равна частоте колебаний источника волны.

Величину характеризующую перемещение волновой поверхности за один период в зависимости от рода среды и частоты колебаний, называют длиной волны. Длину волны измеряют расстоянием, на которое перемещается волновая поверхность за один период колебаний источника волн. Другими словами, учитывая изложенное в § 24.13, можно сказать (рис. 24.14), что длиной волны является расстояние между двумя ближайшими точками бегущей волны на одном луче, которые колеблются в одинаковой фазе. (Отметим, что в расстоянии между двумя любыми точками бегущей волны, которые находятся на одном луче и колеблются в одинаковой фазе, всегда содержится целое число длин волн или четное число полуволн. Если же на луче взять две точки, колеблющиеся в протипоположных фазах, то в расстоянии между ними всегда будет содержаться нечетное число полуволн.)

Для поперечных волн (рис. 24.16) длиной волны является кратчайшее расстояние между двумя ближайшими выпуклостями или впадинами. Для продольных волн (рис. 24.18) длиной волны служит кратчайшее расстояние между центрами двух соседних сгущений или разрежений.

Скорость распространения волн и ее связь с длиной волны и периодом (частотой) колебаний

Вспомним, что при распространении колебаний в среде происходит перемещение фазы (§ 24.13). Скорость распространения колебаний в упругой среде называют фазовой скоростью волны. Так как фазовая скорость в изотропной среде постоянна, то ее можно найти, разделив перемещение фазы волны на время, за которое оно произошло. Поскольку за время Т фаза волны перемещается на расстояние то

(24.22)

Так как имеем

(24.23)

Установлено, что фазовая скорость определяется только физическими свойствами среды и ее состоянием. Поэтому механические волны с разной частотой колебаний в заданной среде распространяются с одинаковой скоростью (заметим, что это верно только при не очень большом различии в частоте колебаний).

Таким образом, определенной частоте колебаний в заданной среде соответствует единственное значение длины волны При этом, как видаю из формулы (24.23), большей частоте соответствуют более короткие волны в среде. Это дает возможность характеризовать волны в среде не частотой (периодом) колебаний частиц в них, а длиной волны Здесь нужно помнить, что при переходе волны из одной среды в другую частота v .и период колебаний Т частиц в ней остаются постоянными, а длина волны изменяется пропорционально изменению скорости . Итак, характеризовать волны их длиной можно только тогда, когда все сравниваемые волны распространяются в одной и той же среде.

Сложение колебаний, происходящих по одной прямой

На практике часто происходит наложение колебаний друг на друга. Например, если на полу стоят два электродвигателя, работающие на разных оборотах, то пол совершает сложное колебание, которое получается вследствие наложения колебаний, вызванных работой каждого двигателя в отдельности. Результирующее колебание может оказаться довольно сложным по своему виду.

Рассмотрим сложение гармонических колебаний одинаковой частоты, которые происходят по одной прямой. Такие колебания можно складывать графически. Имея графики смещений и в зависимости от времени t, график смещения результирующего колебания можно найти алгебраическим сложением смещений и в каждый момент времени (на рис. 24.19, а показано такое сложение для двух точек). Таким образом, результирующее смещение в каждой точке определяется соотношением

(24.24)

Соединив плавной кривой концы полученных таким путем ординат, найдем график результирующего колебания.
Как видно из рис. 24.19, а, при сложении гармонических колебаний одинаковой частоты получается гармоническое колебание той же частоты. Сложение таких колебаний можно выполнять проще, не прибегая к построению графиков.

Пусть складываемые колебания описываются уравнениями

В теории колебаний доказывается, что амплитуду и начальную фазу результирующего колебания можно найти, складывая векторно амплитуды А’ и А»:

(24.25)

Делается это следующим образом. Из произвольной точки О (рис. 24.19, б) проводят горизонтальную полупрямую, от которой отсчитываются начальные фазы. Из точки О проводят векторы А’ и А», положения которых определяются начальными фазами и Амплитуда результирующего колебания А является диагональю параллелограмма, построенного на векторах А’ и А», а угол определяет начальную фазу результирующего колебания. На рис. 24.19, б показана векторная диаграмма колебаний, графики которых изображены на рис. 24.19, а.

Заметим, что А’, А» и А’— это подвижные радиусы складываемых колебаний и результирующего колебания, и векторами их называют условно, поскольку они не имеют отношения к понятию вектора как физической величины. На рис. 24.19, б они изображены в начальный момент времени. (Покажите, что при вращении этих векторов с угловой скоростью (против часовой стрелки) их проекции на вертикальную прямую определяют смещения соответствующих колебаний.)

Отражение волн

Явление отражения волн можно наблюдать с помощью следующего опыта. Поместим линейку так, чтобы ее край немного выступал над поверхностью воды (рис. 24.20, а), и с помощью падающих капель создадим волны на этой поверхности. Тогда будет видно, что у края линейки происходит отражение волн. При этом отраженные волны идут так, как будто они распространяются из точки O₁, расположенной симметрично точке О относительно отражающей поверхности (линейки).

На рис. 24.20, б показана схема отражения волн, распространяющихся из точки О, от поверхности АВ. Рассмотрим отражение волн в точке А. Луч OA называют падающим, а луч О₁А — отраженным. Угол i, составленный падающим лучом и перпендикуляром AD, восставленным из точки падения луча к поверхности, на которую падают волны, называют углом падения, а i’, составленный отраженным лучом и тем же перпендикуляром, называют углом отражения.

На схеме видно, что луч падающий, луч отраженный и перпендикуляр AD в точке А находятся в одной и той же плоскости (в плоскости рисунка).

Покажем, что углы i и i’ равны между собой. В силу симметрии точек О и O₁ (OC—O₁C) треугольники ОАС и O₁AC равны друг другу, поэтому Поскольку то и Это означает, что .

Итак, отражение волн подчиняется двум законам.

1. Луч падающий и луч отраженный лежат в одной плоскости с перпендикуляром к отражающей поверхности, восставленным в точке падения луча.

2. Угол отражения луча равен углу его падения:

(24.26)

Заметим, что на границе раздела двух сред, вообще говоря, происходит не только отражение волн, но и их проникновение в другую среду. Например, на границе воздух — вода продольные волны могут переходить как из воды в воздух, так и из воздуха в воду.

На практике наблюдаются два типичных случая отражения. Пусть поперечная волна идет по шнуру С выпуклостью вперед. После отражения от поверхности АВ (рис. 24.21) волна бежит обратно впадиной вперед. Такой случай называют отражением с потерей полуволны, поскольку после отражения фаза колебаний у фронта волны изменилась на противоположную. Так отражаются волны от твердой поверхности, например, волны на резиновом шнуре от закрепленной точки шнура.

Когда при отражении фаза колебания сохраняется, то потери полуволны не происходит. Такое отражение называют отражением без потери полуволны. В этом случае, если волна до отражения шла выпуклостью вперед, то и после отражения она распространяется выпуклостью вперед.

Стоячие волны

При отражении волн происходит явление наложения колебаний. На рис. 24.20, а видно, как отраженные волны накладываются на основные волны. Это означает, что каждая точка поверхности воды там, где волны перекрывают друг друга, совершает сложное колебание. Если к концу нити, перекинутой через блок D (рис. 24.22), подвесить маленькую гирьку К, а другой конец нити привязать к молоточку звонка, то при колебаниях молоточка по нити бегут волны, которые после отражения в точке D возвращаются к звонку. В результате наложения отраженных волн на основные на нити получаются стоячие волны, названные так потому, что в них нет перемещения фазы. При этом на нити ясно видны точки, которые не колеблются. Эти точки называют узлами (A, В, С и D). Наблюдая за колебаниями нити, можно видеть, что все точки между ближайшими узлами колеблются в одинаковых фазах, но имеют разные амплитуды. Такие точки на нити, амплитуды колебаний которых максимальны, называют пучностями. Например, точка Е на рис. 24.22 является пучностью.

Продолжая наблюдать за нитью, можно увидеть, что узлы и пучности все время находятся в одних и тех же местах нити. Расстояние между соседними узлами составляет половину длины стоячей волны. Оказывается, что фазы точек нити соседних полуволн всегда противоположны. Если в какой-либо момент времени нить занимает положение, изображенное сплошной линией, то через половину периода она займет положение, показанное пунктиром.

В стоячей волне нет такого переноса энергии, как в бегущей волне: сумма энергий всех точек, расположенных на расстоянии четверти длины волны, остается постоянной, хотя между этими точками и происходит обмен энергией. Объясняется это тем, что прямые и отраженные волны переносят энергию в противоположные стороны.

Заметим, что стоячие волны возникают только тогда, когда в расстоянии от источника волн до препятствия, отражающего волны, укладывается целое число четвертей волны.

Интерференция волн

Представим себе, что на поверхности воды распространяются волны, идущие из двух различных точек. Эти волны будут накладываться друг на друга в тех местах, где они встречаются и пересекаются. Однако каждая из волн, пройдя место встречи с другой волной, продолжает распространяться дальше так, как будто этой встречи не было. Это означает, что распространение в пространстве волн от одного источника не мешает распространению в нем других волн. Если волны от разных источников вызывают в каждой точке колебания, происходящие по одной прямой, то при наложении таких волн смещение каждой точки равно алгебраической сумме смещений, создаваемых каждой волной в отдельности. Описанное свойство волн называют суперпозицией.

Когда в среде распространяются волны с разной частотой колебаний, колебание каждой точки оказывается негармоническим. В каждой точке среды разность фаз двух колебаний непрерывно меняется во времени, и устойчивых результирующих колебаний не получается.

Иная картина возникает при распространении волн с одинаковыми частотами колебаний. Источники волн, колеблющиеся с одинаковой частотой, в течение всего времени колебаний сохраняющие постоянную разность фаз, называют когерентными. Волны, создаваемые этими источниками в какой-либо среде, называют когерентными. В каждой точке среды разность фаз колебаний, вызванных когерентными волнами, все время остается постоянной.

При наложении когерентных волн, распространяющихся в какой-либо среде, получается устойчивая картина колебаний точек среды, на которой видно, что одни точки колеблются с большой амплитудой, а другие — с маленькой. Явление взаимного усиления и ослабления колебаний в разных точках среды в результате наложения когерентных волн называют интерференцией. Примером интерференционной картины колебаний точек среды являются стоячие волны на шнуре, так как прямые и отраженные волны когерентны.

Заметим, что для наблюдения интерференции удобнее всего пользоваться когерентными источниками, которые создают гармонические колебания точек среды. В этом случае результирующие колебания точек, получающиеся вследствие наложения волн, будут гармоническими и для их описания можно пользоваться соотношениями, выведенными в § 24.18.

В частности, при наложении таких волн в какой-либо точке среды с противоположными фазами амплитуда ее колебания равна разности амплитуд накладывающихся колебаний, а в случае наложения волн с одинаковыми фазами амплитуда колебания точки будет равна сумме амплитуд накладывающихся колебаний. Если накладываются колебания с одинаковой амплитудой, то в первом случае точка будет сохранять состояние покоя, а во втором — колебаться с удвоенной амплитудой. Примером таких точек являются узлы и пучности в стоячей волне (рис. 24.22). Интерференция когерентных волн на поверхности воды показана на рис. 24.23, где видны линии, на которых точки не колеблются.

На рис. 24.24 изображены два когерентных источника A и В, которые имеют одинаковые фазы и создают в среде волны длиной В случае однородной среды расстояние от выбранной точки, например от точки D, до источника колебаний называют волновым путем. Отметим, что для однородной среды волновой путь совпадает с геометрическим путем, пройденным фронтом волны от источника волн до выбранной точки.

Чтобы установить, в каких точках среды при интерференции волн получится наибольшая (или наименьшая) амплитуда колебаний, пользуются следующим приемом. Находят разность волновых путей от источников волн до выбранной точки, т. е. (BD—AD), и определяют, сколько длин волн укладывается в этой разности. Если в ней уложится нечетное число полуволн, т. е. волны от источников в точку D приходят в противофазе, то в выбранной точке произойдет максимальное-ослабление колебаний. Если разность волновых путей равна четному числу полуволн (или нулю), то в выбранной точке произойдет максимальное усиление колебаний.

Для точки D в разности волновых путей укладывается поэтому в ней получается максимальное ослабление колебаний. Для точки С разность волновых путей (ВС—АС) равна нулю. Это означает, что колебания в ней наложатся одинаковыми фазами, т. е. произойдет максимальное усиление колебаний. (С помощью § 24.18 докажите справедливость изложенного выше приема.)

В заключение заметим, что наличие интерференции в каком-либо явлении служит верным признаком его волнового характера.

Сложение колебаний с кратными частотами. Разложение сложного колебания на гармонические составляющие

Рассмотрено сложение гармонических колебаний с одинаковыми частотами. На практике часто встречаются сложные колебания, которые получаются при наложении нескольких колебаний с кратными частотами. Сложение таких колебаний (рис. 24.25) можно выполнять графически, учитывая, что если колебания происходят по одной прямой, то смещение результирующего колебания в каждый момент времени равно алгебраической сумме смещений и т. д. складываемых колебаний.

На рис. 24.25 изображено сложное колебание , состоящее из трех гармонических колебаний с кратными частотами: (при и ). Колебание с минимальной частотой ( на рис. 24.25) называют первой гармоникой, колебания с кратными частотами ( и т. д.) называют высшими гармониками.

В результате сложения синусоидальных колебаний с кратными частотами получается периодическое несинусоидальное колебание, период которого совпадает с периодом первой гармоники (см. рис. 24.25), поскольку в одном периоде первой гармоники укладывается целое число периодов каждой из высших гармоник. (Покажите, что это так.) Форма сложного колебания может быть самой различной, в зависимости от того, сколько гармоник входит в его состав, какие у них частоты, амплитуды и начальные фазы. На рис. 24.26 приведен пример сложения двух колебаний — первой и третьей гармоник: a) (при причем на рис. 24.26, б третья гармоника сдвинута на половину своего периода.

Возникает вопрос: нельзя ли выполнить обратную задачу — данное негармоническое колебание представить в виде суммы гармонических колебаний, т. е. разложить сложное колебание на гармонические составляющие? Оказывается, можно. Согласно математической теореме Фурье любое периодическое колебание с периодом Т можно представить в виде суммы гармонических составляющих с частотами и т. д. вычислив соответствующие им амплитуды и фазы. Такой прием облегчает изучение сложных колебаний, поскольку к каждой из этих гармоник можно применять законы гармонического колебания.

Обычно фазы гармонических составляющих сложного колебания не представляют интереса, важно знать лишь их частоты и амплитуды. Набор этих частот и амплитуд называется гармоническим спектром несинусоидального колебания. Спектры удобно изображать в виде графиков (рис. 24.27), откладывая по горизонтальной оси частоты (или номера гармоник), а по вертикали — их амплитуды.

На рис. 24.27, а показан спектр колебания, изображенного на рис. 24.25, а на рис. 24.27, б — спектр колебаний, изображенных на рис. 24.26. По спектру нельзя определить форму колебания. Например, колебания, изображенные на рис. 24.26, имеют одинаковые спектры (рис. 24.27, б). Однако по спектру можно определить энергию каждой гармоники (см. (24.21)), что обычно бывает достаточно для характеристики сложного колебания.

Вынужденные колебания. Механический резонанс и его роль в технике

Прикрепим пружинный маятник к кривошипному механизму (рис. 24.28). Не приводя в действие механизм, приведем маятник в колебания по вертикали и подсчитаем частоту его свободных колебаний. Когда силы сопротивления незначительны, то она практически совпадает с частотой собственных колебаний, определяемой выражением (24.16).

Теперь остановим маятник и начнем равномерно вращать механизм с угловой скоростью Точка закрепления пружины при этом будет двигаться возвратно-поступательно вверх-вниз, и на маятник будет действовать внешняя сила, периодически изменяющаяся с круговой частотой . Под действием этой силы маятник будет совершать незатухающие вынужденные колебания с той же частотой .

Будем теперь изменять частоту вынуждающей силы и измерять амплитуду A вынужденных колебаний маятника, дождавшись каждый раз, пока они примут установившийся характер.
При очень медленном вращении механизма ( мала) маятник поднимается и опускается вместе с точкой подвеса на небольшую высоту, не раскачиваясь. При увеличении со он раскачивается все сильнее, а при приближении частоты вынужденных колебаний со к измеренной нами частоте свободных колебаний амплитуда А резко возрастает, достигая максимального значения при совпадении этих частот (рис. 24.29, кривая 1). При дальнейшем увеличении со амплитуда А быстро уменьшается. При очень быстром вращении механизма ( велика) маятник вследствие своей инерции практически неподвижен.

Такую частоту вынуждающей силы, при изменении которой как в большую, так и в меньшую сторону амплитуда вынужденных колебаний системы уменьшается, называют резонансной частотой той системы. Резонансом называют явление быстрого возрастания амплитуды вынужденных колебаний какой-либо системы при приближении частоты вынуждающей силы к резонансной частоте системы.

Резонансная частота системы равна частоте ее свободных колебаний; когда силы сопротивления-малы, то можно считать, что она равна собственной частоте ( на рис. 24.29).

Явление резонанса можно наблюдать и с помощью маятника, подвешенного на нити, если периодически раскачивать точку подвеса в такт со свободными колебаниями маятника. Раскачивая качели, мы тоже подталкиваем их в такт с.их свободными колебаниями. Если же подталкивать качели не в такт с их колебаниями, то они остановятся.

Повторим опыт с нашим маятником (рис. 24.28), погрузив его в стакан с водой. Под действием сил сопротивления амплитуда колебаний в области резонанса сильно уменьшится (кривая 2 на рис. 24.29) и немного уменьшится резонансная частота, поскольку частота свободных колебаний станет меньше. Если еще более увеличить сопротивление, опустив маятник в глицерин, резонанс будет слабо выражен (кривая 3 на рис. 24.29).

Итак, амплитуда колебаний системы при резонансе сильно зависит от сил сопротивления среды и трения. Чем меньше эти силы, тем больше амплитуда колебаний системы. Особенно большие амплитуды колебаний при резонансе получаются, когда силы сопротивления малы. В этом случае колебания при резонансе могут разрушить всю колеблющуюся систему.

Заметим, что тело, амплитуда вынужденных колебаний которого сильно увеличивается только при определенной частоте вынуждающей силы, называют резонатором. Если привести в вынужденные колебания несколько различных резонаторов, то колебания с большой амплитудой возникнут только у того резонатора, у которого резонансная частота совпадает с частотой вынужденных колебаний. На этом принципе основано устройство частотомера — прибора для измерения частоты переменного тока.

В этом приборе на общей планке закреплены упругие пластинки с грузиками на концах (язычки). Пластинки имеют различные частоты собственных колебаний и располагаются в порядке их возрастания. Переменный ток неизвестной частоты пропускается через электромагнит, под действием которого планка с пластинками совершает вынужденные колебания с частотой тока. Одна из пластинок, у которой собственная частота такая же, попадает в резонанс и колеблется сильно, что и позволяет определить частоту тока.

Практическое значение резонанса в природе и технике очень велико. Резонанс встречается не только в механических явлениях. Он используется в электротехнике, оптике и в ядерной физике. На резонансе основана работа радиоприемников, телевизоров и т. п.

Часто резонанс приносит и вред. Например, при определенных частотах звука иногда дребезжит корпус радиоприемника, преждевременно изнашиваются фундаменты, на которых устанавливают ритмично работающие машины, и т. д. В авиации резонанс может привести даже к разрушению самолета во время полета. Поэтому новые модели самолетов испытываются при различных режимах работы двигателей и в самых разнообразных условиях полета. Во время испытаний следят за появлением резонансных колебаний в отдельных деталях самолета, которые при окончательной отработке конструкции должны быть устранены. С помощью теории и опытов можно избежать возникновения резонанса там, где он приносит вред.

Услуги по физике:

Лекции по физике:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Понятие о колебательных процессах. Гармонические колебания.

Колебательные движения – одни из наиболее распространенных видов движения в природе и технике.

Колебательным движением мы будем называть такое движение, при котором параметры характеризующие движение с течением времени повторяются.

Существуют различные виды колебаний:

1. Свободные и вынужденные

2. Затухающие и незатухающие

3. Периодические и непериодические

Свободными называют колебания, происходящие только под действием внутренних сил колебательной системы.

Вынужденными называются колебания, происходящие под действием внешней периодической силы, действующей на колебательную систему.

Незатухающие колебания – колебания, в течении которых энергия колебательной системы не изменяется. В том случае, если энергия уменьшается колебания затухающие. В этом случае энергия превращается в другие ее виды, т.е. происходит ее диссипация ( рассеяние).

Периодические- такие колебания, для которых повторимость параметров происходит через строго постоянный промежуток времени – период. В противоположном случае колебания непереодические.

В зависимости от вида колебаний системы колебания могут быть механические, электрические, электромагнитные и т.д.

Если колебания свободны и незатухающие – собственные колебания.

Собственные периодические колебания получили название гармонических.

Гармонические колебания – простейший вид колебательного движения. На их примере мы изучаем основные закономерности этого движения.

1.2 Амплитуда, период, частота, круговая частота, фаза колебаний.

Гармонические колебания описываются при помощи так называемых гармонических законов: синуса и косинуса.

(1.1)

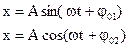
х – параметр, характеризующий отклонение системы от положения равновесия.

А – амплитуда колебаний, максимальное отклонение системы от положения равновесия.

Периодом называется время, за которое система совершает одно полное колебание- Т.

Частота 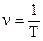(1.2) показывает сколько колебаний совершает система в единицу времени (линейная частота).

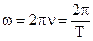
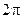
Существует понятие круговой и циклической частоты (1.3) показывающей, сколько колебаний совершает система за единиц времени.

Фаза колебаний – величина, являющаяся аргументом синуса и косинуса.

(1.4)

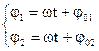
Значение фазы колебаний в начальный момент времени t=0 называется начальной фазой колебания. Это параметр, характеризующий состояние колебательной системы в начальный момент времени. Следует отметить, что начальная фаза может выбираться нами в какой-то степени произвольно в зависимости от того, какой гармонический закон взят нами для описания синус или косинус.

1.3 Скорость и ускорение гармонических колебаний. Основное уравнение динамики гармонических колебаний.

Для вычисления скорости и ускорения возьмем за основной закон синус:

(1.5)

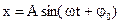
Мы будем рассматривать в данном случае механические колебания, но отметим, что все закономерности, полученные нами, будут справедливы и для колебаний другой природы.

(1.6)

(1.7)

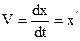
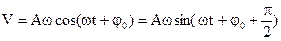
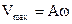
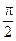
Формула (1.7) показывает, что 1) изменение скорости стечением времени тоже протекает по гармоническому закону. (1.8) 2) Изменение скорости со временем происходит со сдвигом фаз на по отношению к изменению смещения со временем.

Находим ускорение, как производную скорости по времени.

(1.9)

(1.10)

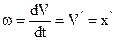
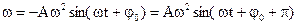
Формула (1.10) показывает, что изменение ускорения со временем также происходит по гармоническому закону. Максимальное значение ускорения вычисляется по формуле.

(1.11)

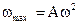
А – сдвиг фаз для ускорения.

Соотношение (1.10) можно записать также в виде

(1.12)

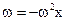
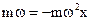
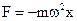
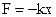
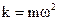
Если умножить левую и правую части (1.12) на массу, то получим: , а с учетом 2-го закона Ньютона:

(1.13)

(1.14)

(1.15)

Формула (1.14) означает, что гармонические колебания происходят тогда, когда на колебания тела действует сила, линейно зависимая от смещения. Примером такой силы является сила упругости.

Если сила подчиняется соотношению (1.14), но не является упругой, то сила называется квазиупругой.

Гармонические колебания в механических системах происходят под действием либо упругих либо квазиупругих сил.

Перепишем соотношение (1.12) следующим образом

(1.16)

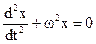
Уравнение (1.16) называется основным уравнением динамики гармонических колебаний. Оно является обыкновенным дифференциальным уравнением 2-го порядка. Решением его является гармонический закон синус или косинус.

1.4 Сложение колебаний одного направления, векторные диаграммы.

Гармонические колебания можно описывать при помощи следующего метода.

Представим себе, что в окружности точка О вращается радиус-вектор, длина которого равна амплитуде колебаний, а угловая скорость вращения совпадает с циклической частотой. Тогда проекции r на ось x и y будут находиться по формулам:

Такой способ описания колебаний называют методом векторных диаграмм. Его удобно применять в том случае, когда необходимо складывать колебания.

Рассмотрим случай, когда точка одновременно участвует в двух гармонических колебаниях, происходящих вдоль одного и того же направления. А нам надо найти результирующее колебание.

(1.17)

(1.18)

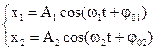
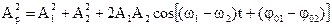
Если каждое из колебаний описывать данным методом, то амплитуду результирующего колебания можно найти в каждый момент времени как векторную сумму амплитуд исходных колебаний. Тогда по теореме косинусов амплитуда вычисляется по формуле (1.18).

Если частоты не равны, то, как следует из (1.18), амплитуда результирующего колебания будет зависеть от времени. В результате более сложное движение, чем гармонические колебания.

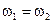
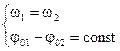
Рассмотрим простой случай, когда частоты совпадают и кроме того разность фаз есть константа.

(1.19)

Колебания, для которых выполняется условие (1.19) называются когерентными. При условии (1.19) соотношение (1.18) упрощается и принимает следующий вид:

(1.20)

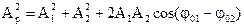
Результат, вычисляемый по формуле (1.20) полностью зависит от разности фаз.

Рассмотрим два частных случая:

(1.21)

(1.22)

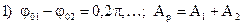
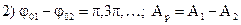
В первом случае колебания в результате сложения усиливают друг друга, а во втором ослабляют.

Такое явление называется интерференцией:

Это явление взаимного усиления или ослабевания когерентных колебаний в результате их сложения.

Определим начальную фазу колебания (рис. 2). Из рис. 2 видно, что

таким образом:

(1.23)

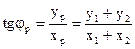
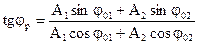
1.5 Сложение взаимно перпендикулярных колебаний.

Возможны ситуации, когда точки одновременно участвуют в колебаниях происходящих во взаимно перпендикулярных направлениях. В этом случае результат сложения может быть гармоническое колебание или какое-либо другое, более сложное движение.

(1.24)

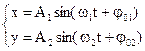
Сложить эти колебания означает найти уравнение результирующего колебания или если это не удается, то траекторию движения, в котором участвуют точки в результате сложения колебаний. Для иллюстрации рассмотрим два примера

Разделим одно уравнение (1.24) на другое. В результате получим:

(1.25)

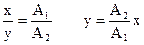
(1.15) – уравнение траектории и прямой линии идущей следующим образом:

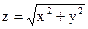
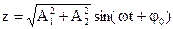
Траекторию движения точки вдоль прямой линии отклоняют от начала отсчета то в одну, то в другую сторону, причем отклонение z находится по теореме Пифагора: (1.26). Если в (1.26) подставить (1.24) получим:

(1.27)

(1.27) – гармонический закон, только А_р находим по теореме Пифагора:

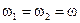
в этом случае уравнения имеют вид:

Выразим синус, косинус, возведем в квадрат и получим:

(1.28)

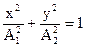
В этом случае уравнение (1.28) – уравнение эллипса, приведенного к главным осям.

ГЛАВА 2. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР

2.1 Механические гармонические колебания, математический и физический маятники, пружинный маятник.

Математический маятник – материальная точка, подвешенная на невесомой и не растяжимой нити и колеблющаяся около положения равновесия.

Физический маятник – тело произвольной формы, подвешенное в точке, расположенной выше центра масс колеблющееся около положения равновесия.

Математический маятник – частный случай физического маятника, поэтому в начале рассмотрим колебания физического маятника и найдем частоту и период колебаний.

Точка О – точка подвеса, точка С – центр масс, 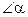— угол отклонения от положения равновесия, d – плечо силы тяжести.

Колебания этого маятника можно рассмотреть как вращательное движение данного тела около центра вращения точки О, тогда для описания можно взять за основу основной закон динамики вращательного движения.

(2.1)

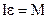
Моментом силы является момент силы тяжести.

(2.2)

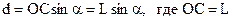
С учетом (2.2) формула для момента силы принимает следующий вид:

(2.3)

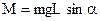
Подставляем (2.3) в (2.1) с учетом направления момента и получаем:

(2.4)

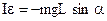
«-» говорит о том, что момент и угловое ускорение направлены в противоположные стороны.

Будем рассматривать малые отклонения для которых 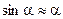, тогда с учетом формулы для углового ускорения:

получаем следующее соотношение:

(2.5)

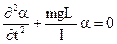
Уравнение (2.5) имеет вид основного уравнения динамики гармонических колебаний, частота которых находится по формуле:

(2.6)

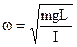
Тогда период колебаний найдется по формуле:

(2.7)

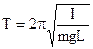
Точка О – точка в которой нить закреплена.

Обозначим длину математического маятника l=OC, тогда момент инерции колеблющейся точки относительно точки О будет равен:

(2.8)

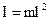
Если подставить (2.1) в (2.6) и (2.7) и учесть, что в данном случае l=L, то получим для циклической частоты и периода:

(2.9)

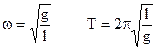
Если сравнить формулы (2.9) с формулами (2.6) и (2.7), то мы увидим, что для того чтобы эти формулы один и тот же вид необходимо, чтобы

(2.10)

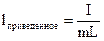
Эта величина называется приведенной длиной физического маятника. Она равна длине такого математического маятника период колебаний которого совпадает с периодом колебаний данного физического маятника.

Приводимая длина физического маятника меньше длины данного тела.

Рассмотрим пружинный маятник – тело некоторой массы m подвешенное на пружину. Предположим, что в положении равновесия сила тяжести, действующая на это тело уравновешено F_упр пружины, а когда мы отклоняем систему из положения, то движение происходит только под действием F_упр. Тогда 2-ой закон Ньютона имеет вид:

(2.11)

(2.12)

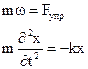
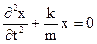
Уравнение (2.12) – уравнение гармонических колебаний, частота которых находится по формуле:

(2.13)

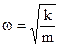
а период колебаний:

(2.14)

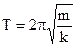
Рассмотрим, как ведет себя энергия колебательной системы в данных случаях. В случае гармонических колебаний скорость находится по формуле:

, тогда

(2.15)

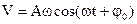
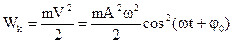
Потенциальная энергия в случае упругих или квазиупругих сил находится:

(2.16)

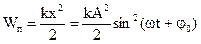
Если найти полную энергию

(2.17)

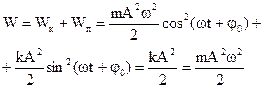
Формула (2.17) показывает, что полная энергия постоянна и действует закон сохранения энергии. Полная энергия колебаний равна максимальному значению кинетической или потенциальной энергии.

2.2 Электрические гармонические колебания в колебательном контуре.

Рассмотрим простую электрическую колебательную систему – колебательный контур.

L- катушка индуктивности, С- емкость конденсатора, R- сопротивление.

Запишем для этого закон Ома:

(2.18)

– сила тока (2.19)

(2.20)

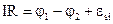
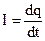
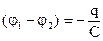
— разность зарядов на обкладках конденсатора.

(2.21)

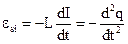
Если подставить (2.20) и (2.21) в (2.18) и выполнить некоторые преобразования, то имеем:

(2.22)

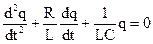
Наличие сопротивления в цепи приводит к рассеиванию энергии. Поэтому гармонические колебания будут тогда, когда сопротивление контура станет равным нулю, тогда уравнение (2.22) упрощается:

(2.23)

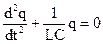
Уравнение (2.23) – уравнение гармонических колебаний, заряда q, причем частота колебаний находится:

(2.24)

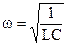
,а период колебаний:

(2.25)

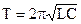
Формулы (2.24) и (2.25) – формулы Томпсона.

Колебательный контур в котором отсутствует сопротивление называется идеальным. С точки зрения энергии в этом контуре происходит превращение энергии катушки в энергию конденсатора и наоборот:

(2.26)

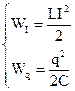
W_I— энергия магнитного поля,

W_q— энергия электрического поля.

2.3 Свободные затухающие колебания. Логарифмический декремент затухания. Добротность

Рассмотрим затухающие колебания на примере механических и электрических колебаний. В случае механических колебаний они будут затухающими, если внутри системы существуют силы трения или силы сопротивления.

Мы рассмотрим тот случай, когда эти силы пропорциональны скорости.

(2.27)

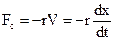
r- коэффициент сопротивления.

Тогда 2-ой закон Ньютона имеет следующий вид:

(2.28) или:

(2.29)

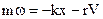
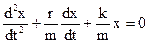
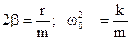
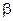
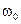
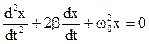
Введем обозначение: (2.30)

— коэффициент затухания, — собственная частота колебаний. Теперь уравнение (2.29) имеет вид:

(2.31)

Уравнение (2.31) – основное уравнение динамики затухающих колебаний.

Решение этого уравнения можно записать следующим образом:

(2.32)

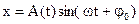
Где 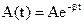— затухает по этому закону (2.33)

Частота затухающих колебаний не совпадает с собственной частотой колебаний, а находится по формуле:

(2.24)

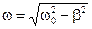
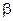
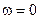
Возможен случай, когда так велико, что . Такие колебания называются ангармоническими. В этом случае затухающие колебания происходят за время равное периоду колебания. При небольших значениях колебания происходят более медленно, и график зависимости x от t имеет вид:

Уменьшается по экспоненциальному закону.

Натуральный логарифм двух последующих амплитуд различается на период Т называется логарифмическим декрементом затухания.

Пусть 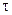— время, за которое амплитуда уменьшится в е раз.

Где n – общее число колебаний

Добротность Q обратно пропорциональна логарифмическому декременту затухания.

Рассмотрим электрические колебания. Вернемся к уравнению:

Обозначим в этом уравнении

(2.35)

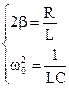
Тогда уравнение электрических колебаний принимает вид уравнения (2.31), т.е. основного уравнения затухающих колебаний.

Следовательно, и формулы (2.32), (2.33) и (2.34) будут справедливы для электрических колебаний. Единственно надо заменить смещение х зарядом q.

2.4 Вынужденные колебания механического осциллятора под действием синусоидальной силы. Амплитуда и фаза при вынужденных колебаниях. Резонансные кривые.

Рассмотрим случай, когда на колеблющееся тело действует внешняя периодическая сила. Будем считать, что эта сила изменяется по гармоническому закону.

(2.36)

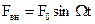
Запишем 2-ой закон Ньютона:

(2.37)

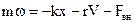
После всех преобразований получим формулу:

(2.38)

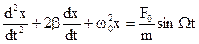
Уравнение (2.38) – основное уравнение динамики вынужденных колебаний.

С точки зрения теории дифференциальных уравнений это неоднородное уравнение потому его решение складывается их двух слагаемых:

1) Общее решение соответствующего однородного уравнения, т.е. уравнения затухающих колебаний.

2) Частного решения данного неоднородного уравнения.

(2.39)

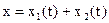
В этом случае говорят, что вынужденные колебания не установились, а наблюдается так называемый переходный режим. С течением времени первое слагаемое в (2.39) стремится к нулю, так как это оно описывает затухающие колебания, и, начиная с некоторого момента времени, можно записать что

x=x₂(t), где х₂ – частное решение неоднородного уравнения (2.38)

Такие колебания называются установившимися вынужденными колебаниями. И это частное решение имеет вид:

(2.40)

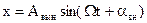
где А_вын находится по формуле:

(2.41)

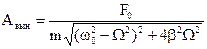
Начальная фаза находится из соотношения:

(2.42)

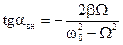
Из формулы видно, что амплитуда вынужденных колебаний может принимать разные значения, в зависимости от соотношения частоты колебаний и частоты вынуждающей силы. Поэтому соотношение (2.41) можно исследовать на максимум. Ясно, что это соотношение будет достигать максимального значения тогда, когда подкоренное выражение

(2.43)

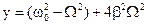
достигнет минимального значения. Находим производную, y=0.

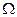
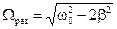
После сокращения и приведения подобных членов получаем:

(2.44)

где 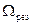— резонансная частота. При этом если частота вынуждающей силы совпадает с резонансной частотой, то наблюдается резкое возрастание амплитуды вынужденных колебаний – резонанс.

Из формулы (2.44) видно, что в случае незатухающих колебаний , когда резонансная частота совпадает с собственной частотой:

(2.45)

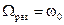
График зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы называется резонансной кривой (РК). РК имеет ярко выраженный максимум в точке .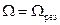

Острота пика (максимума) зависит от коэффициента затухания. Эту зависимость можно получить аналитически. Если в формулу для амплитуды вынужденных колебаний (2.41) подставить значение резонансной частоты (2.44). В результате получится формула:

(2.46)

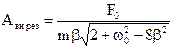
Из формулы (2.46) видно при 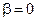правая часть обращается в бесконечность. Таким образом РК будут иметь следующий вид:

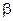
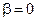
По мере увеличения максимум РК будет передвигаться к началу координат и сама РК является все более и более пологой. При максимум РК равен бесконечности и приходится строго на собственную частоту колебаний.

2.5 Осциллятор, как спектральный прибор. Фурье – разложение. Физический смысл спектрального разложения.

В природе и технических достижениях часто встречаются более сложные виды колебаний, чем гармонические колебания. Их изучение представляет собой трудную задачу, для облегчения которой существует метод сведения одного сложного колебания к множеству простых колебаний. Одним из таких методов является разложение сложного колебания в бесконечный ряд, членами которого являются гармонические функции, содержащие кратные частоты. Такое разложение называется Фурье-разложением и соответствует ряду Фурье.

Предположим, что сложное колебание описывается некоторой произвольной функцией S(t)=f(t) ,тогда разложение этой функции в ряд Фурье будет иметь следующий вид:

(2.47)

(2.48)

(2.49)

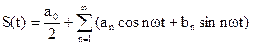
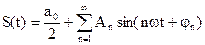
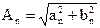
где частоты 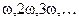называются гармониками. — основная или 1-ая гармоника. Остальные называют дополнительными гармониками.

Коэффициенты a_n и b_n называют коэффициентами ряда Фурье и они вычисляются по формулам Эйлера – Фурье:

(2.50)

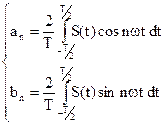
Периодические колебания имеют дискретный ряд Фурье. А непериодические колебания имеют непрерывный ряд Фурье.

Совокупность частот, по которым происходит разложение данного колебания, называется не совокупностью частот, а совокупностью самих колебаний, на которые происходит разложение. В зависимости от того, как распределены гармоники, спектры могут быть линейчатыми (в случае дискретного распределения гармоники) или сплошными (в случае непрерывного распределения гармоник).

Разложением сложных колебаний в ряд Фурье позволяет в большинстве случаев заменить изучение этого колебания изучением нескольких достаточно простых колебаний. Это происходит в том случае, когда коэффициенты ряда Фурье являются убывающими и следовательно сам ряд можно оборвать при некотором конкретном значении (n не равно бесконечности). В этом заключается физический смысл спектрального разложения.

2.6 Модулированные колебания. Спектр амплитудно-модулированного колебания.

Если какой-либо из параметров колебаний меняется с течением времени по определенному заданному закону, то говорят о модуляции колебаний. Колебания в этом случае называются модулированными. Наиболее широко распространены два вида модуляции:

1) Модуляция амплитудная,

2) Модуляция частотная.

В 1-ом случае с течением времени изменяется амплитуда колебаний, во 2-ом – частота.

Изменение этих параметров должно происходить медленнее, чем сами колебания. Это означает, что время изменения параметров в должно быть меньше чем период колебаний.

Рассмотрим более подробно амплитудное модулированное колебание, если немодулированное колебание зависит негармоническим законом.

(2.51)

то соответствующие модулированные колебания для случая амплитудной модуляции будет описываться законами следующего вида:

(2.52)

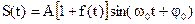
Здесь функция несет в себе основную информацию об ограничении амплитуды. На нее накладываются ограничения:

(2.53)

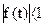
Наиболее часто встречаются случаи, когда функция сама является периодической. В этом случае частота ее изменения должна быть гораздо меньше, чем частота самого колебания.

(2.54)

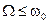
Модулированное колебание можно разложить в спектральный ряд. Покажем это на примере, когда функция является гармонической:

(2.55)

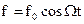
Если подставить (2.55) в (2.52), то получим следующую формулу:

(2.56)

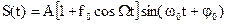
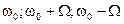
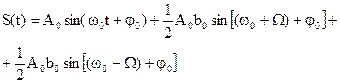
Такое колебание можно разложить в спектральный ряд, состоящий из трех слагаемых, частоты которых принимают значения . Непосредственной подстановкой можно убедиться, что соответствующее разложение имеет вид:

(2.57)

Таким образом, амплитудно-модулированное колебание разлагается в спектр, состоящий из трех колебаний.

2.7 Нелинейный осциллятор. Физические системы, содержащие нелинейность.

Если колебания описываются линейными дифференциальными уравнениями, то они называются линейными колебаниями.

В противоположном случае колебания называются нелинейными.

Общий вид нелинейного дифференциального уравнения, описывающего колебания следующий:

Если функция f имеет вид 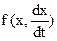(2.58), то колебания называются автономными.

Если эта функция имеет вид f=f(x) (2.59), то колебания называются консервативными.

Мы до сих пор рассматривали случай, когда функция f(x) была линейной. В механике эта функция соответствует возвращающей силе, приведенной к единице массы. Таким образом, механические колебательные системы будут нелинейными в том случае, когда возвращающая сила зависит от смещения х нелинейно.

Для электрических колебаний роль х выполняет заряд и в простейшем случае (линейном) функция f(q) подчиняется линейному соотношению, аналогично закону Гука в механике.

В более сложных случаях в электрических колебательных системах могут возникать нелинейности связей, с наличием в системе либо обратных связей, либо зависимости от временных параметров, характеризуют всю систему (индуктивность L, емкость С).

Для ангармонических колебаний характером связи является зависимость периода колебаний от амплитуды колебаний. В общем случае эту зависимость можно описать следующей формулой:

(2.60)

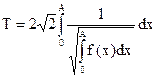
Из этой формулы видно, что конкретный вид определен видом функции f(x).

Подставим (2.61) в (2.60) и проинтегрируем:

(2.62)

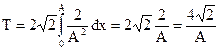
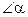
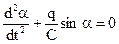
2) Нелинейными являются колебания математического маятника в том случае, когда он отклоняется от положения равновесия на угол больше . В этом случае уравнение колебаний имеет следующий вид:

(2.63)

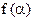
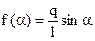
Таким образом, функция имеет вид:

(2.64)

Если подставить (2.64) в (2.60), то получим зависимость периода колебаний от угла отклонения маятника от положения равновесия:

(2.65)

— максимальное значение угла отклонения от положения равновесия.

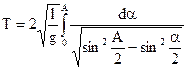
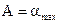
Зависимость (2.65) в явном виде не интегрируется.

Интеграл называется эллиптическим. Но зависимость можно разложить в степенной ряд.

(2.66)

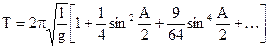
Из формулы (2.66) видно, что обычная формула математического маятника получается из случая, когда под рядом в квадратных скобках остается только первое слагаемое.

ГЛАВА 3. ВОЛНОВЫЕ ПРОЦЕССЫ

3.1 Волны. Уравнение волны и волновое уравнение. Плоская и сферическая синусоидальные волны. Амплитуда, частота, фаза и длина волны, волновое число. Фазовая скорость.

Рассмотрим колебания не материальной точки, а некоторой частицы среды, связанной с другими частицами тем или иным взаимодействием. В этом случае колебание данной частицы будет вызывать (благодаря взаимодействию) колебания соседних с ней частиц. То есть в процесс колебаний будут вовлекаться все новые и новые частицы среды и колебания будут распространятся в данной среде – волновой процесс, а сами колебания, распространяющиеся в среде — волны.

Если взаимодействия между частицами среды упругие, то такая среда называется упругой, и волны, в которой они распространяются тоже упругие.

Обычно, для волны является характерно то, что происходит процесс переноса энергии от точки к точке данной среды без переноса вещества – волна бегущая. Кроме бегущей существуют стоячие волны, для которых является характерным отсутствие переноса энергии.

Линия, вдоль которой происходит перенос энергии, называется лучом.

По касательной к этой линии, в общем случае, направлена скорость.

1. Продольные упругие волны, когда частицы среды колеблются в направлениях скорости распространения волны.

2. Поперечные волны, в этом случае частицы среды колеблются в направлениях перпендикулярных скорости распространения волны.

Существует особый вид волн, которые возникают на поверхности жидкости. Они называются поверхностными волнами. Для них характерно то, что частицы жидкости в процессе колебаний движутся по сложным траекториям. И это движение происходит одновременно и вдоль скорости, и перпендикулярно скорости.

Поперечные и продольные, упругие волны могут возникать в тех или иных веществах в зависимости от упругих свойств этих веществ. Так если вещество отличается упругостью по отношению к изменению объема, в таком веществе возникают только продольные волны.

Если вещество отличается упругостью по отношению к изменению формы, то в нем могут возникать поперечные волны.

В случае поперечных волн частицы среды колеблются в плоскости перпендикулярной скорости распространения волны, причем в общем случае направление этих колебаний может в течение времени меняться, хаотично оставаясь на этой плоскости. Такая волна называется естественной (неполяризованной). Если каким-то образом упорядочить направление колебаний, то волна становится поляризованной, а само явление упорядочения направления колебаний называется поляризацией.

Если ввести на плоскости, в которой происходит колебание частицу среды, оси X Y, то результирующее колебание можно представить как сумму двух взаимно перпендикулярных. В этом случае траектория движения частицы, в зависимости от разности фаз складываемых колебаний, может быть:

1) Прямой линией (поляризация называется линейной).

2) Эллипсом или окружностью (поляризация называется эллиптической или круговой).

Процесс распространения колебаний можно описать математически при помощи уравнения, которое связывает параметр, характеризующий отклонение точек среды от положения равновесия с пространственными и временными координатами.

Если обозначить параметр буквой S-смещение от положения равновесия, то уравнение волны:

Если колебания точек среды происходит по гармоническому закону, то волна называется синусоидальной или гармонической.

Геометрическое место точек среды колебаний в одинаковых фазах называют волновой поверхностью или фронтом волны.

Если волновые поверхности представляют собой плоскости параллельные друг другу, то волна называется плоской.

Плоская синусоидальная волна – простой вид волны. Волна распространяется вдоль только одного направления. Луч представляет собой прямую линию, которая обычно совпадает с осью X. Уравнение волны упрощается:

Выведем уравнение для плоской синусоидальной волны:

Колебания в каждой точке описываемые при помощи обычного гармонического закона, по колебаниям в точке отстающей от данной точки на расстояние X будут запаздывать на время 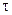=x/v, которое необходимо волне, чтобы распространится от одной точки к другой. Таким образом колебания в произвольной точке будут описываться в общем случае соотношением:

S=S(t ‘ )=S(t-τ)=S(t- 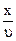) (3.2)

Если вместо s подставить гармонический закон:

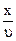
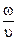
S=A sin (ωt ‘ + φ_o)=A sin [ω (t- )+φ_o]=A sin (ωt- x+φ_o). (3.3)

Уравнение (3.3) – уравнение плоской синусоидальной волны.

Если волновые поверхности являются концентрическими сферами или поверхностями, то волна называется сферической.

Она описывается аналогичным уравнением в котором роль X выполняет расстояние от центра сферических поверхностей, где располагается источник волны, до данной точки.

S=A(r) sin(ωt- 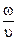r+φ_o) (3.4)

Вторым отличием сферической волны является то, что амплитуда колебаний зависит от расстояния r .

A(r)= 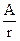(3.5)

Точно также как колебания можно было описать с помощью дифференциальных уравнений (основных уравнений динамики) волновой процесс можно описать с помощью дифференциального уравнения, которое называется волновым уравнением.

Это уравнение относительно параметра S , так как этот параметр зависит от двух переменных, то это уравнение является дифференциальным уравнением частных производных.

Для плоской синусоидальной волны уравнение имеет вид:

(3.6)

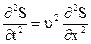
(3.6) – простейшее волновое уравнение.

В общем виде, оно имеет вид:

(3.7)

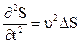
где 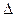, так как оператор Лапласа

Сферическая синусоидальная волна описывается уравнением (3.7), в котором оператор Лапласа описывается в сферических координатах.

Рассмотрим уравнение волны и параметры в него входящие:

S=A sin ( )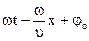

А – амплитуда колебаний частиц среды, которая одновременно является и амплитудой волны.

ω — циклическая частота колебаний среды, циклическая частота волны.

υ, Т – частота и период колебаний, частота и период волны.

Выражение являющееся аргументом синуса называется фазой волны.

Φ= 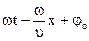(3.10)

Фаза волны отличается от фазы колебаний, так как зависит от двух параметров X и Z. Каждая волна характеризуется длиной.

Длина волны – расстояние, которое проходит волна за время равное периоду колебаний.

= = (3.11)

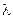
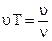
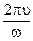
Длиной волны называют кратчайшее расстояние между двумя точками волны, колеблющимися в одинаковых фазах.

С учетом (3.11) отношение 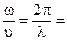k (3.12)

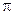
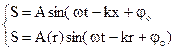
Где k – волновое число, которое показывает сколько раз длина волны укладывается на 2 единицы длины.

(3.13)

Скорость с которой распространяются волновые поверхности называется фазовой скоростью.

Формулу для нее можно получить, если продифференцировать по времени соотношение (3.14).

t-kx+ =const

k dx=0

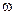
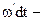
v= 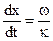(3.15)

3.2 Принцип суперпозиции волн. Групповая скорость и ее связь с фазовой скоростью, распространение волн в средах с дисперсией.

Если колебания точек среды описываются линейными уравнениями, то такая среда называется линейной. Для линейных сред справедлив принцип суперпозиций волн. Согласно которому, если в данной среде распространяются одновременно несколько волн, то каждая точка среды участвует в колебаниях принадлежащих каждой волне независимо от колебаний принадлежащим другим волнам, поэтому результирующее колебание описывают параметрами, которые находят как суммы параметров исходных колебаний.

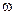
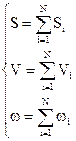
Это такие параметры: смещение-S, скорость-V, ускорение- .Таким образом принцип суперпозиции можно записать математически в виде 3-х соотношений.

(3.18)

При помощи принципа суперпозиции можно представлять синусоидальные волны в виде некоторого числа синусоидальных волн.

Рассмотрим такое представление на примере квазисинусоидальной волны. Такая волна получается при сложении 2-х синусоидальных волн одинаковой амплитуды и очень близких частот.

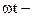
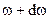
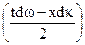
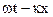
S=A sin ( kx)+A sin [( )t-(k+dk)x]=2Acos ·sin( ) (3.19)

Соотношение (3.19) можно переписать в виде:

S=A_г sin( 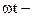kx) (3.20)

A_г=2A cos 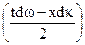(3.21)

Совокупность волн из которых складывается произвольная несинусоидальная волна называется спектром волны. Также спектром называют совокупность частот этих волн.

Группа волн называется волновым пакетом и скорость с которой она распространяется отличается от фазовой скорости. Эта скорость называется групповой скоростью. Ее можно определить следующим образом: зафиксировать точку волнового пакета, которой соответствует постоянное значение амплитуды А_г и установить скорость движения этой точки. Это и будет групповая скорость.

td 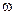-xdk=const (3.22)

u= 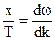(3.23)

Групповая скорость- скорость переноса энергии волновым пакетом, в этом заключается его физический смысл.

Установим связь между групповой скоростью и фазовой:

(3.24)

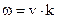
Подставим (4.24) в (3.23)

u= 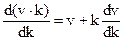(3.25)

Если учесть, что

(3.26)

(3.27)

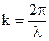
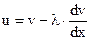
Существуют среды, в которых фазовая скорость волны зависит от длины волны или частоты. Такие среды называются диспергирующими. А само явление зависимости называется дисперсией волн. Если волновой пакет распространяется в такой среде, то волны его составляют движение с различными фазовыми скоростями и в результате волновой пакет меняет свою форму-«расплывается».

3.3 Интерференция монохроматических волн. Временная и пространственная когерентность. Интерференция синусоидальных волн. Стоячие волны.

Рассмотрим две синусоидальные волны, каждая из которых имеет свою собственную амплитуду, частоту и начальную фазу. Кроме того будем рассматривать такой случай, когда источники этих волн находятся на различных расстояниях r₁ и r₂ до той точки, в которой происходит сложение колебаний.

(3.28)

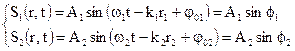
Если применить для сложения колебаний точек среды, которые они испытывают благодаря наличию этих двух волн, метод векторных диаграмм, то для амплитуды результирующего колебания можно записать следующую формулу:

(3.29)

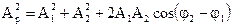
А для разности фаз:

(3.30)

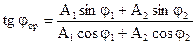
Из формулы (4.29) видно, что амплитуда результирующего колебания зависит от разности фаз:

(3.31)

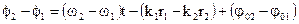
В общем случае эта разность фаз зависит от времени и результирующая амплитуда будет функцией t. Если разность частот:( 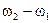) достаточно велико, то изменение результирующей амплитуды будет происходить так быстро, что зарегистрировать прибором можно будет только среднее значение амплитуды, взятое за достаточно продолжительный промежуток времени τ.

Вычислим среднее значение квадрата результирующей амплитуды:

За знак интеграла можно вынести те величины, которые не зависят от времени:

(3.32)

за время τ>>T изменяется от +1 до –1, поэтому интеграл, выражающий его среднее значение, обращается в ноль. Следовательно, получаем:

(3.33)

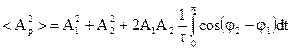
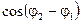
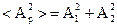
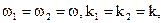
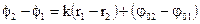
Вычислим результирующую амплитуду в том случае, когда колебания точек среды являются когерентными. В этом случае поэтому (3.34)

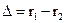
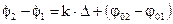
Введем (3.35) и перепишем (3.34) с учетом (3.35)

(3.36)

Если подставить (3.36) в (3.29), то мы увидим, что возможны ситуации, когда результирующая амплитуда будет максимальной или минимальной.

В общем случае разность фаз должна иметь следующее значение:

(3.37)

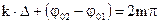
Во втором случае: 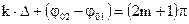(3.38)

Где m-любое целое число.

Условия (3.37) и (3.38) можно преобразовать для геометрической разности хода.

1-е условие дает:

2-е условие дает:

Объединив эти два условия в одно, получим (3.39).

Наиболее интересным является тот случай, когда начальные фазы колебания совпадают.

(3.40)

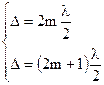
То есть все определяется геометрической разностью хода складываемых волн, при этом, если выполняется условие максимума, то для результирующей амплитуды:

В случае минимума:

При сложении когерентных волн мы получаем устойчивую во времени пространственную картину, в которой наблюдаются максимумы и минимумы в различных точках пространства. Такое явление называется явлением интерференции. Картина называется интерференционной картиной, а условия максимума и минимума называются условиями интерференционных максимумов и минимумов.

Стоячие волны – частный случай интерференции, когда складывают волны, которые имеют одинаковую амплитуду и распространяются на встречу друг другу, вдоль некоторого направления. Пусть это направление будет направлением оси Х, тогда уравнение складываемых волн будет иметь вид:

Первая волна распространяется в сторону положительного направления оси Х, а вторая волна ей на встречу, поэтому мы получаем разные знаки перед пространственной частью фаз этих волн.

(3.41)

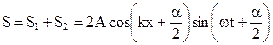
Таким образом, уравнение результирующей волны разбивается на два сомножителя. Один из которых зависит только от пространственных координат, а второй только от временных это позволяет переписать уравнение следующим образом:

(3.42)

(3.43)

-амплитуда стоячей волны.

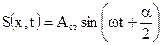
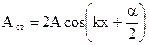
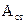
Как видно из уравнения (3.43) амплитуда меняется по гармоническому закону.

Там где наблюдается максимум амплитуды, находятся так называемые кучности стоячей волны. Там где наблюдаются минимумы, находятся узлы стоячей волны.

Их положения можно найти, используя условия максимума для правой части (3.43).

(3.44)

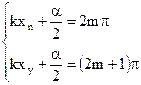
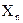
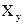
где -координаты кучности.

-координаты узла.

Длиной стоячей волны называют расстояние между соседними кучностями или соседними узлами.

3.4 Энергия волны. Вектор Умова.

При распространении упругих волн каждая точка среды участвует в упругих колебаниях, поэтому имеет как кинетическую, так и потенциальную энергию. Полная энергия точки в каждый момент времени t равна суммарной кинетической и суммарной потенциальной. По мере распространения волны происходит перенос энергии от одной точки среды к другой. Введем плотности энергии:

(3.45)

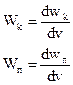
Можно показать, что первая величина выражается следующей формулой:

(3.46)

-плотность данной среды, v₁-скорость, которую имеют точки среды благодаря участию в колебании. Мы предполагаем, что эта скорость одна и та же для всех точек среды находящихся в объеме dv.

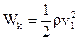
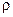
Аналогично для плотности потенциальной энергии существует формула:

ε 2 (3.47)

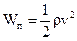
v-фазовая скорость волны, ε — относительная деформация среды.

Между скоростью V и V₁ существует связь, которая выражается следующей формулой:

Отсюда видно, что:

(3.49)

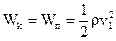
Следовательно, плотность полной энергии:

(3.50)

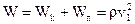
Если волна гармоническая, то выражение плотности полной энергии имеет вид:

(3.51)

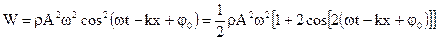
При помощи формулы (4.51) удобно находить среднее значение плотности полной энергии. Если усреднять за время большее чем период колебаний, то среднее значение от косинуса будет равно нулю, и мы получим:

(3.52)

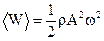
То есть среднее значение полной энергии равно половине от максимального значения. Выведем понятие потока энергии как величину численно равную энергии, которая переносится через некоторую площадку в единицу времени перпендикулярно этой площадке.

Общая формула для этой величины имеет вид:

(3.53)

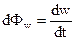
Рассмотрим площадку dS, ориентированную под некоторым углом α по отношению к направлению распространения волны и найдем, какая энергия будет переноситься волной через эту площадку. Для этого вычислим W заключенную в заштрихованном объеме.

(3.54)

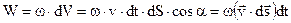
Подставим (3.54) в (3.53):

(3.55)

(3.56)

-вектор плотности потока энергии (Умова).

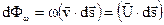
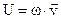
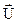
Используя вектор Умова можно находить конечный поток энергии:

(3.57)

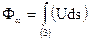
Можно ввести понятие интенсивности волны. Это величина равна модулю среднего значения вектора Умова.

(3.58)

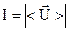
ГЛАВА 4. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И ИХ СВОЙСТВА

4.1 Скорость распространения электромагнитных возмущений. Волновое уравнение для электромагнитных волн. Свойства электромагнитных волн. Электромагнитная природа световых волн.

Электромагнитными волнами называют совокупность переменных электрического и магнитного полей распространяющихся в пространстве.

Очень важная особенность электромагнитных волн заключается в том, что для их распространения не нужна какая либо среда. Более того, с максимальной скоростью и без потерь энергии, лучше всего электромагнитные волны распространяются в вакууме. Эта особенность электромагнитных волн долгое время воспринималась ученными как нечто невероятное, поэтому много сил было потрачено на поиски такой среды возмущения, которая представляла бы собой электромагнитные волны (теория эфира).

Запишем первые два уравнения Максвелла:

(4.59)

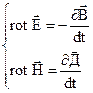
Используем связь между векторами:

ε (4.60)

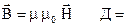
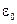
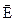
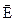
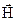
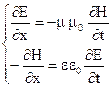
Кроме того, рассмотрим простейший случай, когда вектора и зависят только лишь от одной переменной пространственной координаты от Х, то есть одномерный случай, тогда:

(4.61)

Первое уравнение из этой системы дифференцируем по Х, второе по t.

(4.62)

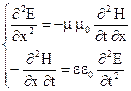
Исключаем смешанные производные:

(4.63)

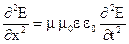
В этом уравнении связаны вторые производные. Оно имеет вид волнового уравнения для вектора .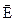

Для того чтобы это уравнение совпадало с волновым необходимо ввести обозначения.

; (4.64)

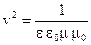
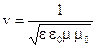
Если продифференцировать первое уравнение (4.61) по t, а второе по Х, то в результате точно таких же преобразований получим такое же уравнение вида (4.63) для вектора :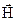

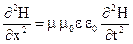
(4.65)

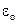
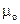
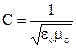
В выражение для v (4.64) входят две постоянные: и , выведем новую постоянную:

(4.66)

С- электродинамическая постоянная.

Таким образом, мы получили волновые уравнения для векторов напряженностей электрического и магнитного полей. Это означает, что мы доказали существование электромагнитных волн, механизм распространения которых, состоит в следующем:

Переменное во времени электрическое поле благодаря тому, что оно представляет собой вихревой электрический ток, порождает переменное во времени магнитное поле, которое при помощи явления электромагнитной индукции порождает переменное во времени электрическое поле и так далее.

Скорость распространения электромагнитной волны может быть записана в форме:

(4.67)

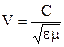
Если волна распространяется в вакууме, то 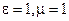, тогда V=C (4.68)

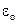
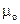
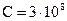
Если в формулу (4.66) подставить численные значения и , то в результате вычислений мы получим:

м/с

Известно, что именно такое значение имеет скорость распространения света в вакууме. Из этого совпадения Максвелл вывел предположение о том, что световые волны являются по своей природе именно электромагнитными волнами. Дальнейшее изучение электромагнитных волн доказало справедливость предположения Максвелла.

Электромагнитные волны обладают следующими свойствами:

1). Возможность распространения в вакууме.

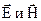
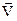
2). Можно доказать, что вектора в электромагнитном поле взаимно перпендикулярны и перпендикулярны вектору (скорости волны), причем

\|	следующая лекция ==>
Супергетеродинний приймач	\|	Отражение и преломление электромагнитных волн на границе раздела двух диэлектриков.

Дата добавления: 2016-04-19 ; просмотров: 3613 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

источники:

http://natalibrilenova.ru/mehanicheskie-kolebaniya-i-volnyi/

http://helpiks.org/7-88343.html