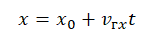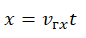Если координаты частицы задана уравнением x 1 2t

Тесты на экзамен по физике (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5

1. Какая из приведенных ниже формул выражает понятие скорости:

В) ;

2. Какая из приведенных ниже формул выражает модуль скорости:

А) ;

3. Какая из приведенных ниже формул выражает понятие ускорения:

D) ;

4. Какая из приведенных ниже формул выражает тангенциальное ускорение:

D) ;

5. Какая из приведенных ниже формул выражает нормальное ускорение:

А)

6. Определить из графика V(t) путь, пройденный телом за 4с:

7. Определить из графика V(t) ускорение: (м/с2)

8. Скорость точки определяется выражением V=(4t-8) м/с. Чему равно ускорение:

9. Скорость точки определяется выражением V=(4t-8) м/с. Чему равно начальная скорость:

10. Что называется нормальным ускорением:

С) Составляющая полного ускорения, характеризующая изменение вектора скорости по направлению;

11. Что называется тангенциальным ускорением:

Е) Составляющая полного ускорения, характеризующая изменение вектора скорости по величине;

12. Материальная точка движется по прямой согласно уравнению х=3+4t. Зависимость скорости точки от времени на графике изображается кривой:

13. Материальная точка движется по прямой согласно уравнению: х=2t+t2-t3. Зависимость скорости точки от времени на графике изображается кривой:

14. Материальная точка движется по прямой согласно уравнению: х=2t+t3. Зависимость скорости точки от времени на графике изображается кривой:

15. Материальная точка движется по прямой согласно уравнению: х=4t-t2. Зависимость скорости точки от времени на графике изображается кривой:

16. Материальная точка движется по прямой согласно уравнению: x=3+t2. Зависимость скорости точки от времени на графике изображается кривой:

17. Точка движется по прямой согласно уравнению: х=4-6t+t2. В какой момент времени ее скорость равна нулю (t, c).

18. Точка движется по прямой согласно уравнению: х=3+6t2-t3. В какой момент времени ее ускорение равно нулю (t, c).

19. Точка движется по прямой согласно уравнению: х=5-2t+t2. В какой момент времени ее ускорение равно 2 м/с2 (t, c).

20. Точка движется по прямой согласно уравнению: х=4-6t+t3. Чему равно ускорение точки в момент времени t=0,5 c (м/с2).

21. Координаты материальной точки массой 2кг, движущейся в плоскости, изменяются согласно уравнениям: х=2+t2, y=3-t3. Чему равна ее скорость в момент времени t=1c: (м/с)

22. Координаты материальной точки массой 2кг, движущейся в плоскости, изменяются согласно уравнениям: х=2+t2, y=3-t3. Чему равен ее импульс (Н. с) в момент времени t=1c: (м/с)

23. Координаты материальной точки массой 2кг, движущейся в плоскости, изменяются согласно уравнениям: х=2+t2, y=3-t3. Чему равна ее кинетическая энергия (Дж) в момент времени t=1c: (м/с)

24. Координаты материальной точки массой 2кг, движущейся в плоскости, изменяются согласно уравнениям: х=2+t2, y=3-t3. Чему равно ее ускорение (м/с2) в момент времени t=1c: (м/с)

25. Координаты материальной точки массой 2кг, движущейся в плоскости, изменяются согласно уравнениям: х=2+t2, y=3-t3. Какая сила действует на это тело в момент времени t=1c:

26. На шайбу массой 500г, имевшую начальную скорость 10 м/с в течение 2 с действует сила трения 1 Н. Какой путь (м) пройдет шайба за это время:

27. Уравнение движения точки, движушейся по прямой х = A+Bt+Ct3. чему равно ускорение в момент времени t=2c, если С = 0,2 м/с:

28. Половину пути поезд прошел со скоростью км/час, вторую половину пути он двигался со скоростьюкм/час. Найдите среднюю скорость поезда.

29. S-модуль перемещения материальной точки, L – путь точки. Какие возможны соотношения между этими величинами:

30. Движение тела описывается уравнением (м). Чему равна средняя скорость тела на второй секунде движения:

31. Угол поворота вращающегося тела задан уравнением . Чему равна угловая скорость тела:

32. Угол поворота вращающегося тела задан уравнением . Чему равна угловое ускорение тела:

33. Угол поворота вращающегося тела задан уравнением . Какому из приведенных условий соответствует движение тела:

А) const;

34. Угол поворота вращающегося тела задан уравнением . Чему равна угловая скорость (рад/с):

35. Угол поворота вращающегося тела задан уравнением . Чему равно угловое ускорение (рад/с2):

36. Скорость материальной точки, движущейся в плоскости XY, изменяется со временем по закону . Какое из выражений определяет модуль скорости:

Е) , м/с.

37. Скорость материальной точки, движущейся в плоскости XY, изменяется со временем по закону . Какое из выражений определяет ускорение:

38. Какое из выражений описывает правильно зависимость ускорения от времени для частицы, движущейся по прямой по закону :

D) ;

39. Какое из выражений описывает правильно зависимость скорости от времени для частицы, движущейся по прямой по закону :

A) ;

40. Какое из выражений описывает правильно зависимость начальной скорости от времени для частицы, движущейся по прямой по закону :

B) ;

41. Какому типу движения точки m соответствует приведенный рисунок:

С) Криволинейному ускоренному;

42. Какому типу движения точки m соответствует приведенный рисунок:

D) Равномерному по окружности;

43. Какому типу движения точки m соответствует приведенный рисунок:

D) Криволинейному замедленному;

44. Какому типу движения точки m соответствует приведенный рисунок:

А) Прямолинейному равноускоренному;

45. Какому типу движения точки m соответствует приведенный рисунок:

С) Прямолинейному равнозамедленному;

46. На рисунке представлена траектория движения камня, брошенного под углом к горизонту. Как направлено ускорение камня в точке А траектории, если сопротивлением воздуха пренебречь:

47. Твердое тело вращается вокруг оси Z. Зависимость угла поворота от времени t описывается законом , где А и В положительные постоянные. В какой момент тело остановится:

Уравнение координаты при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Уравнение координаты — зависимость координаты тела от времени:

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x₀ = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с 2 . Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v₀ = 0 м/с.

В момент времени t = 10 c координата автомобиля равна:

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
Построить уравнение вида x₁ = x₂.
Найти время встречи двух тел t_встр.
Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату x_встрч.

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

x = 3t = 3∙6 = 18 (м).

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

Построить графики x1(t) и x2(t).
Найти точку пересечения графиков.
Пустить перпендикуляр из этой точки к оси ОХ.
Значение точки пересечения — координата места пересечения двух тел.

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с 2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с 2 , достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два

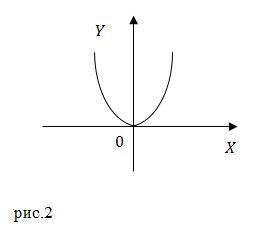
Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

Алгоритм решения

Определить характер движения материальной точки.
Записать уравнение координаты материальной точки.
С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.

Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет вид: 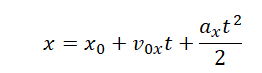Ветви параболы смотрят вверх. Это значит, что коэффициент перед квадратом переменной величины (времени) стоит положительный коэффициент. Следовательно, a_x>0. Поэтому варианты «б» и «г» исключаются. Остается выяснить, чему равна скорость: она равна нулю (как в ответе «а») или меньше нуля (как в ответе «в»)? Моменту времени t=0 соответствует точка, являющая вершиной параболы. Когда ветви параболы смотрят вверх, в ее вершине скорость тела всегда равна нулю, так как эта точка лежит на границе между отрицательной и положительной скоростью. Отсюда делаем вывод, что верный ответ «а».Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Записать исходные данные.
Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
Выразить скорость грузовика из уравнения его движения.
Записать уравнение движения мотоциклиста.
Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
Подставить время в формулу скорости грузовика и вычислить ее.

Решение

Координата встречи грузовика и мотоциклиста: x = 150 м.
Время запаздывания мотоциклиста: t_запазд = 5 с.
Ускорение, с которым мотоциклист начал движение: a = 3 м/с 2 .

Запишем уравнение движения грузовика:

Так как начальная координата равна нулю, это уравнение примет

Отсюда скорость движения грузовика равна:

Запишем уравнение движения мотоциклиста:

Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:

Найдем время, через которое грузовик и мотоциклист встретились:

Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Траектория движения

Определение и основные понятия траектории движения

Во многих задачах интерес представлю не только перемещения материальных точек в пространстве, но и траектории их движения.

Линию, которую описывает частица при своем движении, называется траекторией движения.

В зависимости от формы траектории механическое движение можно разделить на:

прямолинейное движение, траекторией движения точки в этом случае является прямая линия;
и криволинейное перемещение (траектория — кривая линия).

Форма траектории зависит от выбора системы отсчета. В разных системах отсчета траектории могут быть представлены разными линиями, могут быть прямыми и кривыми.

При движении точки с постоянным ускорением, которое описывает уравнение:

Уравнение траектории движения

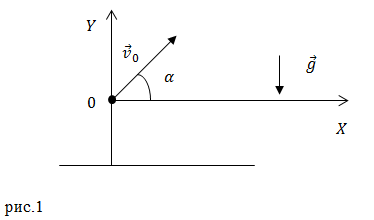
Рассмотрим свободное движение тела около поверхности Земли. Начало координат разместим в точке бросания тела (рис.1). Оси координат направим так, как изображено на рис.1.

Тогда уравнение движения тела (1) в проекциях на координатные оси декартовой системы координат принимает вид системы из двух уравнений:

Для того чтобы получить уравнение траектории движения тела ($y=y(x)$) следует исключить время движения тела из уравнений (2) и (3). Выразим из уравнения (2) $t$ и подставим его в выражение (3), получим:

Выражение (4) это уравнение параболы, проходящей через начало координат. Ее верви направлены вниз, так как коэффициент при $x^2$ меньше нуля.

Вершина этой параболы находится в точке с координатами:

Найти координаты вершины траектории можно при помощи известных правил исследования функций на экстремум. Так, положение максимума функции $y(x)$ определяют, приравнивая к нулю первую производную ($\frac$) от нее по $x$.

Обратимость движения

Из представления о траектории можно конкретизировать смысл обратимости механического движения.

Пусть частица движется в силовом поле таком, что ее ускорение в любой точке обладает определенной величиной, не зависящей от скорости. Как будет двигаться эта частица, если, в какой то точке ее траектории направление скорости заменить противоположным? С точки зрения математики это эквивалентно замене $t\ $ на $-t$ для всех уравнений. Уравнение траектории время не содержит, получается, что частица будет перемещаться «вспять» по той же самой траектории. При этом отрезки времени между любыми точками траектории будут одинаковы при прямом и обратном движении. Всякой точке траектории ставится в соответствие определенное значение величины скорости независимо от направления движения по данной траектории. Данные свойства наглядны в колебательных движениях маятника.

Все сказанное выше справедливо тогда, когда можно пренебречь любым сопротивлением движению. Обратимость движения существует, когда выполняется закон сохранения механической энергии.

Параметры траектории движения

Положение точек системы отсчета можно определять при помощи разных способов. В соответствии с этими способами описывают и движение точки или тела:

Координатная форма описания движения. Выбирается система координат, в ней положение точки характеризуют тремя координатами (в трехмерном пространстве). Это могут быть координаты $x_1=x,x_2=y,x_3=z$, в декартовой системе координат. $x_1=\rho ,x_2=\varphi ,x_3=\ z$ в цилиндрической системе и т.д. При перемещении точки координаты являются функциями времени. Описать движение точки — это значит указать эти функции: \[x_1=x_1\left(t\right);;\ x_2=x_2\left(t\right);;\ x_3=x_3\left(t\right)\left(6\right).\]
При описании движения в векторной форме положение материальной точки задает радиус-вектор ($\overline$) по отношению к точке, которую принимают начальной. В этом случае вводят точку (тело) отсчета. При перемещении точки вектор $\overline$ постоянно изменяется. Конец этого вектора описывает траекторию. Движение задает выражение: \[\overline=\overline\left(t\right)\left(7\right).\]
Третьим способом описания движения является описание с помощью параметров траектории.

Путь — это скалярная величина, равная длине траектории.

Если траектория задана, то задачу описания движения сводят к определению закона движения вдоль нее. При этом выбирается начальная точка траектории. Любая другая точка характеризуется расстоянием $s$ по траектории от начальной точки. В таком случае движение описывают выражением:

Пусть по окружности радиуса R равномерно перемещается точка. Закон движения точки по окружности в рассматриваемом методе запишем как:

где $s$ — путь точки по траектории; $t$ — время движения; $A$ — коэффициент пропорциональности. Известными являются окружность и точка начала движения. Отсчет положительных величин $s$ совпадает с направлением перемещения точки по траектории.

Знание траектории движения тела во многих случаях существенно упрощает процесс описания движения тела.

Примеры задач с решением

Задание: Точка движется в плоскости XOY из начала координат со скоростью $\overline=A\overline+Bx\overline\ ,\ $где $\overline$, $\overline$ — орты осей X и Y; $A$,B — постоянные величины. Запишите уравнение траектории движения точки ($y(x)$). Изобразите траекторию. \textit<>

Решение: Рассмотрим уравнение изменения скорости частицы:

Из этого уравнения следует, что:

Для получения уравнения траектории следует решить дифференциальное уравнение (1.3):

Мы получили уравнение параболы, ветви которой направлены вверх. Эта парабола проходит через начало координат. Минимум этой функции находится в точке с координатами:

Задание: Движение материальной точки в плоскости описывает система уравнений: $\left\< \begin x=At. \\ y=At(1+Bt) \end \right.$, где $A$ и $B$ — положительные постоянные. Запишите уравнение траектории точки.

Решение: Рассмотрим систему уравнений, которая задана в условии задачи:

Исключим время из уравнений системы. Для этого из первого уравнения системы выразим время, получим:

Подставим вместо $t$ правую (2.2) часть во второе уравнение системы (2.1), имеем:

источники:

http://spadilo.ru/uravnenie-koordinaty-pri-ravnouskorennom-pryamolinejnom-dvizhenii/

http://www.webmath.ru/poleznoe/fizika/fizika_95_traektorija_dvizhenija.php