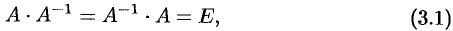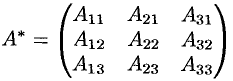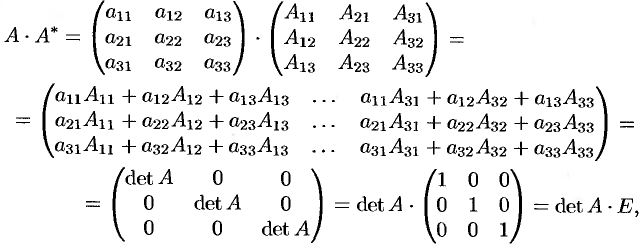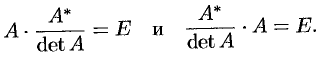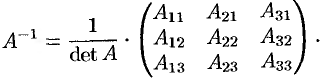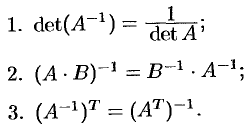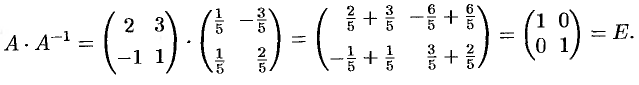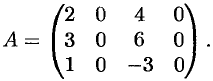Решение матричных уравнений: теория и примеры
Решение матричных уравнений: как это делается
Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,
где x — неизвестное.
А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.
Итак, матричным уравнением называется уравнение вида
где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.
Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B , обе его части следует умножить на обратную к A матрицу 

По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: 

Так как E — единичная матрица, то E ⋅ X = X . В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A , слева, на матрицу B :

Как решить матричное уравнение во втором случае? Если дано уравнение
то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A , и умножать матрицу B на неё справа:



Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как 
Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения

Решение матричных уравнений: примеры
Пример 1. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A :

Наконец, находим неизвестную матрицу:
Пример 2. Решить матричное уравнение

Пример 3. Решить матричное уравнение

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Находим неизвестную матрицу:
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.
Пример 4. Решить матричное уравнение

Решение. Это уравнение первого вида: A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A , и делаем это легко, так как определитель матрицы A равен единице:

Находим неизвестную матрицу:
Пример 5. Решить матричное уравнение

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Находим неизвестную матрицу:
Пример 6. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C , то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Найдём матрицу, обратную матрице B .
Сначала найдём определитель матрицы B :

Найдём алгебраические дополнения матрицы B :
Составим матрицу алгебраических дополнений матрицы B :

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B :

Находим матрицу, обратную матрице B :

11. Решение матричных уравнений
Рассмотрим простейшие матричные уравнения вида А×Х = В (14) и Х×А = В (15).
Возможны два случая: 1) матрица А Квадратная невырожденная; 2) матрица А — либо вырожденная, либо прямоугольная.
1) Если А – квадратная и |А| ¹ 0, то уравнения (14) и (15) имеют единственное решение каждое: Х = А-1×В и Х = В×А-1 соответственно, если эти произведения определены. И не имеют решения, если они не определены.
2) А – квадратная матрица, но |А| = 0, либо А — прямоугольная матрица. Если матрица А Имеет размерность M´n, а матрица В – Размерность Р´к, то, при M ¹ Р уравнение (14) не имеет решения, а при N ¹ к не имеет решения уравнение (15). Если же M = Р , то в уравнении (14) матрица Х Должна иметь К столбцов, а в уравнении (15) она должна иметь Р Строк. Решение этих матричных уравнений сводится к решению систем линейных уравнений.
Пример 5. Найдите матрицу Х, Если А×Х = В, Где А = 
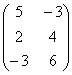
Из примера 5 следует, что матрица А Имеет обратную, поэтому Х = А-1×В. Используя найденную в примере 5 матрицу А-1, Получим Х = 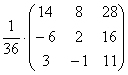

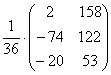
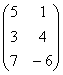
Пример 6. Найдите матрицу Х, Если Х×А = В, где А = 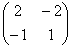
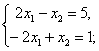
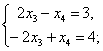
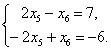
Невырожденные матрицы
Невырожденные матрицы
Основные понятия
Пусть 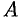
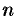
Квадратная матрица 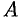
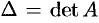
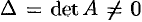
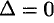
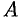
Матрицей, союзной к матрице 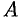
где 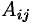
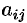
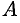
Матрица 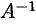
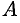
где 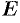
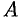
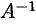
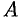
Обратная матрица
Теорема 3.1. Всякая невырожденная матрица имеет обратную.
Проведем доказательство для случая матрицы 3-го порядка. Пусть

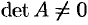
Составим союзную матрицу
и найдем произведение матриц 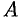
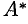
Здесь мы использовали свойства 7 и 8 определителей (см. п. 2.2).
Аналогично убеждаемся, что
Равенства (3.2) и (3.3) перепишем в виде
Сравнивая полученные результаты с определением (3.1), получаем
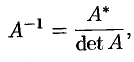
Отметим свойства обратной матрицы:
Пример №3.1.
Найти 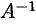
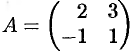
Решение:
1) Находим 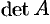
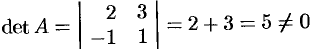
2) Находим 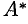
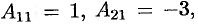
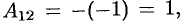
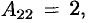
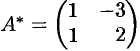
3) Находим 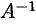
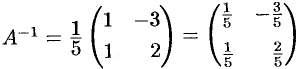
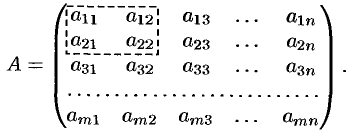
Ранг матрицы
Рассмотрим матрицу 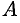
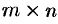
Выделим в ней 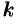
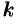
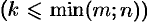
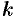
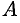
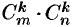
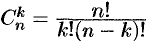
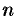
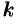
Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается 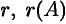
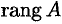
Очевидно, что 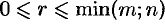
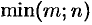
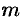
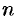
Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.
Пример №3.4.
Найти ранг матрицы:
Решение:
Вес миноры 3-го порядка равны нулю. Есть минор 2-го порядка, отличный от нуля 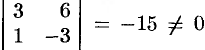
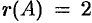
Отметим свойства ранга матрицы:
1. При транспонировании матрицы ее ранг не меняется.
2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.
3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы (см. с. 18).
Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-uchebnoe-posobie-z-i-andreeva/11-reshenie-matrichnykh-uravnenii
http://lfirmal.com/nevyirozhdennyie-matritsyi/