Если перейти к полярной уравнение

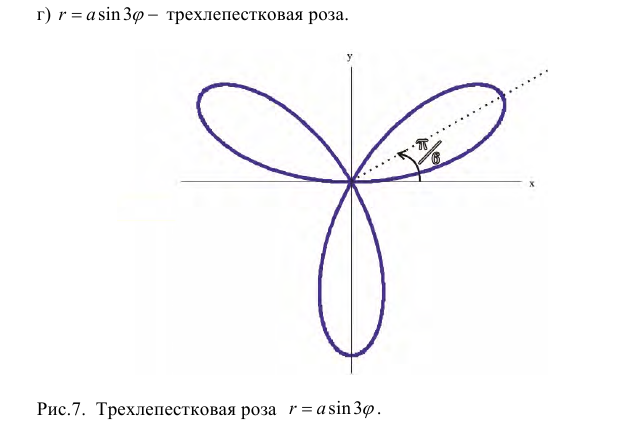
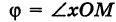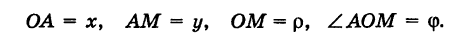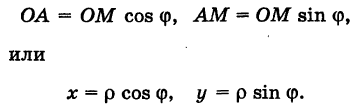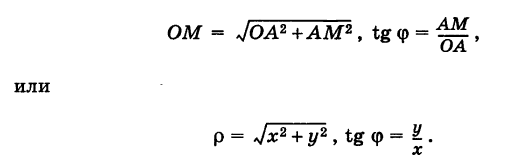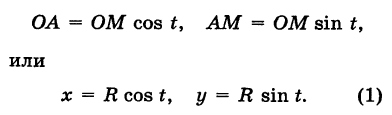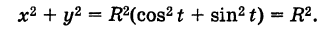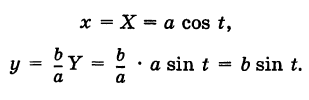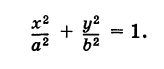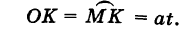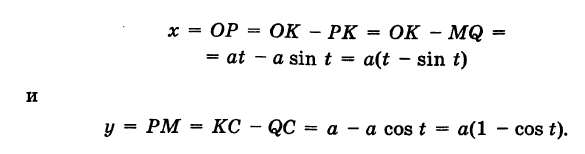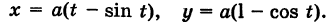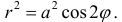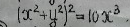Полярные координаты — определение и вычисление с примерами решения

Содержание:

Полярные координаты. параметрические уравнения линии

Полярные координаты

Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.

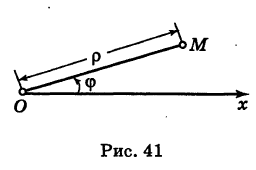
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).

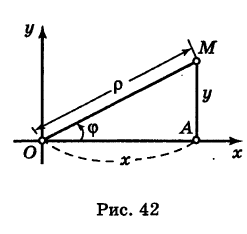
Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол

Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.

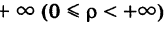
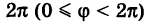
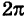
Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до и значения ф от 0 до , при этом, как мы условились, угол ф отсчитывается от полярной оси против хода часовой стрелки. Однако в некоторых вопросах приходится рассматривать углы, большие , а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по направлению движения часовой стрелки.

Связь между прямоугольными и полярными координатами

Рассмотрим переход от полярных координат к прямоугольным и обратно.

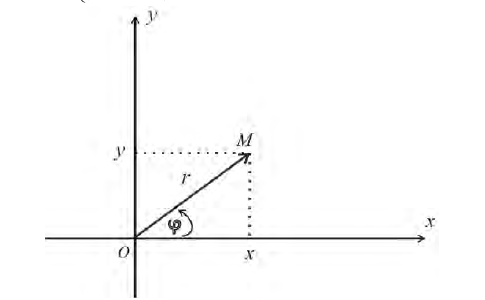
Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).

Тогда для произвольной точки М имеем

Считая угол ф острым, из прямоугольного треугольника АОМ находим

Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты. Далее, из этого же прямоугольного треугольника АОМ получаем

Так выражаются полярные координаты точки через ее прямоугольные координаты.

Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.

Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.

Пример:

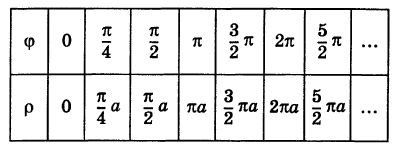
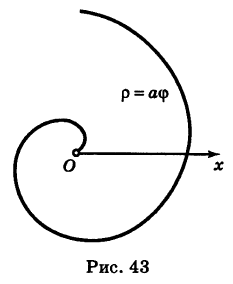
Рассмотрим кривую 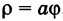, где а — некоторое положительное число. Эта кривая называется спиралью Архимеда. Для ее построения составляем таблицу соответственных значений ф и р:

По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).

Параметрические уравнения линии

Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты 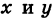, рассматривать так называемые параметрические уравнения линии, дающие выражения текущих координат х и у в виде функций от некоторой переменной величины t (параметра). Параметрические уравнения играют важную роль, например, в механике, где координаты х и у движущейся точки М (х, у) рассматриваются как функции времени (уравнения движения).

Пример:

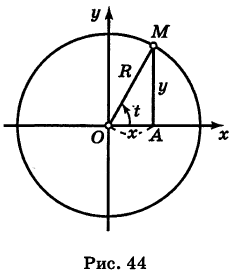
Выведем параметрические уравнения окружности.

Пусть М 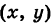— произвольная точка окружности радиуса R с центром в начале координат (рис. 44). В определяемом ею прямоугольном треугольнике АОМ обозначим угол хОМ через t. Тогда, очевидно, будут иметь место равенства

Это и есть параметрические уравнения окружности.

Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:

Пример:

Выведем параметрические уравнения эллипса.

Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где

За параметр t примем угол, образованный радиусом ON окружности с положительным направлением оси Ох: . Используя формулы (2), имеем

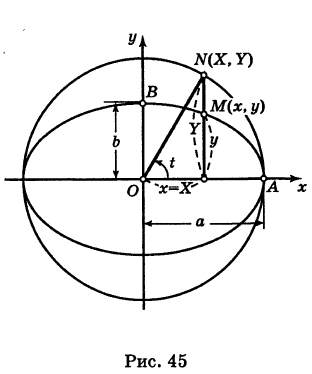
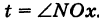
Таким образом, параметрические уравнения эллипса с полуосями а и b есть

Исключив из уравнений (3) параметр получим каноническое уравнение эллипса

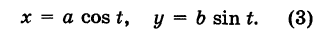
Имея параметрические уравнения линии, можно по точкам построить ее.

Пример:

Решение:

Составляем таблицу значений:

Нанося точки с соответствующими координатами (х, у) на плоскость Оху и соединяя их линией, получим искомую кривую (рис. 46).

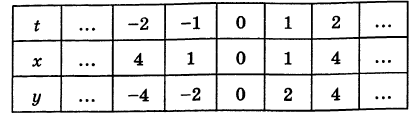
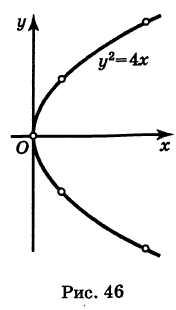
Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим 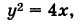т. е. каноническое уравнение параболы.

Параметрические уравнения циклоиды

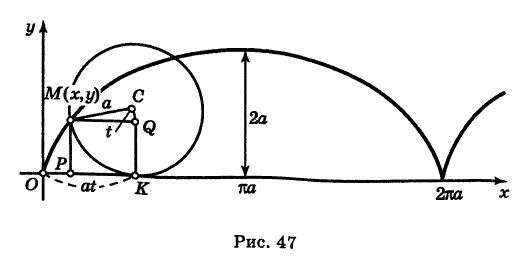
Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).

Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем

Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:

Таким образом, параметрические уравнения циклоиды есть

Полярная система координат

Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат Оху . Пусть М(х, у) – точка на плоскости, M ≠ 0. Полярными координатами точки М называются числа r − длина ее радиус-вектора (полярный
радиус) и ϕ − угол, образованный радиус-вектором с положительным направлением оси Ох (полярный угол), 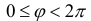. Точка О при этом называется
полюсом, а полуось Ох – полярной осью.
Замечание. Зависимость между прямоугольными (х, у) и полярными ( , ) r ϕ
координатами точки М задается в виде: 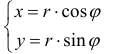(1)

Рис.1. Полярные координаты точки.
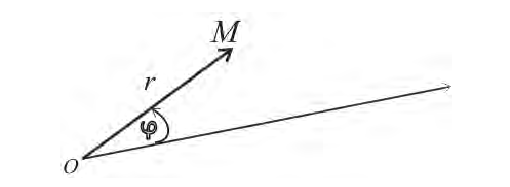
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:

Пример 1.

Построим на плоскости линию, заданную уравнением:
− лемниската.
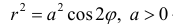
Решение.

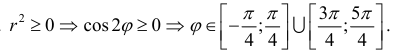
Вычислим значения r при различных значениях ϕ :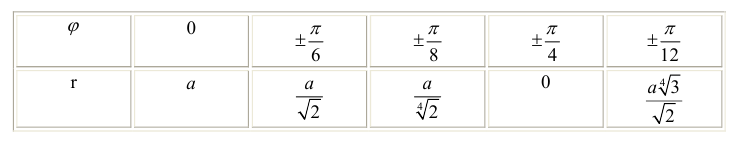

Проводим лучи из начала координат под углами ϕ к оси Ох и на них откладываем
отрезки длины r , получим :

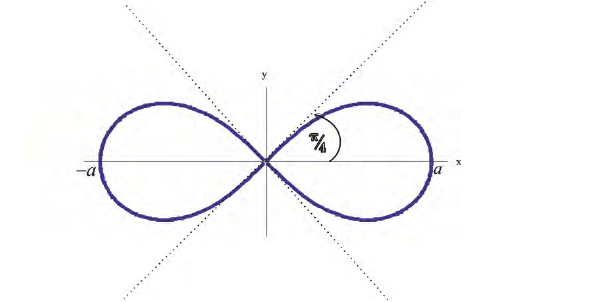
Рис.3. Лемниската

Пример 2.

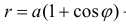
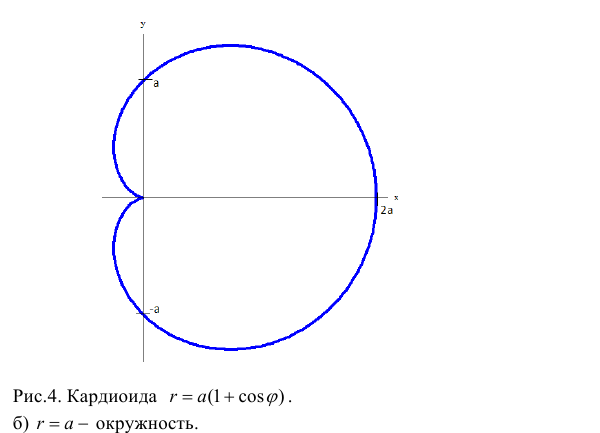
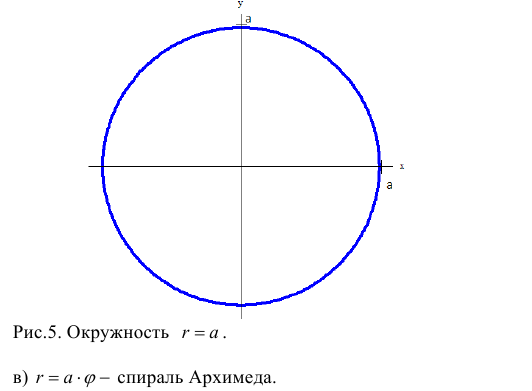
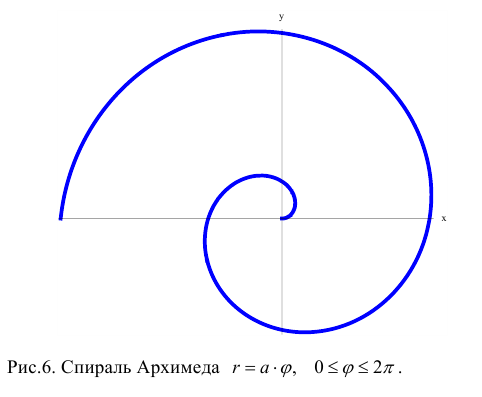
а) Построим кривую − кардиоида. Рассуждая, как в примере 1 получим:




Замечание. Если в определении 1 отбросить требование 0 ≤ ϕ 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).

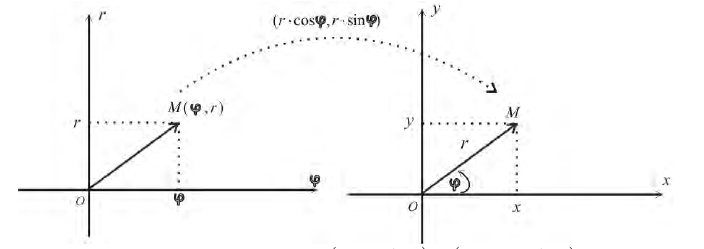
При этом, если r > 0, то векторы 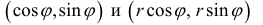сонаправлены, если r

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Задача 31542 Перейти в уравнение кривой к полярным.

Условие

Перейти в уравнение кривой к полярным координатам и построить кривую

Решение

x=r*cos φ
y=r*sin φ
x^2+y^2=r^2

Подставляем в данное уравнение:
(r^2)^2=10r^3cos^3 φ
r=10cos^3 φ

cos^3φ >0 в четвертой и первой четвертях

φ =-π/2⇒ r=10*0^3=0 Откладываем на луче -π/2 0, т. е получаем точку (0;0) на плоскости
φ =-π/3⇒ r=10*(1/2)^3=10/8=5/4
φ =-π/4⇒ r=10*(1/2sqrt(2))≈
φ =-π/6⇒ r=10*(3sqrt(3)/8)≈
φ =0⇒ r=10*1=10 Точка (10;0) на плоскости хОу

φ =π/6⇒ r=10*(3sqrt(3)/8)≈
φ =π/4⇒ r=10*(1/2sqrt(2))≈
φ =π/3⇒ r=10*(1/2)^3=10/8=5/4
φ =π/2⇒ r=0*0^3=0

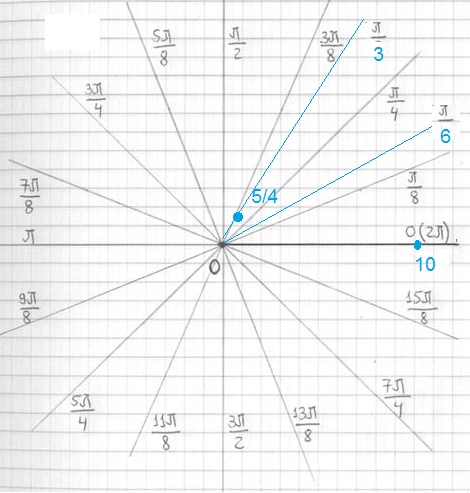
График см рис.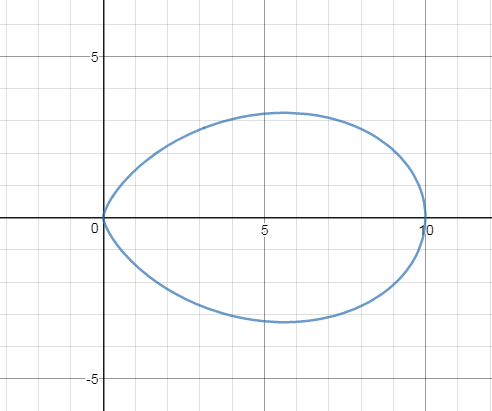

Можно подробнее о построении графика, пожалуйста Я просто никак понять не могу =(

Полярная система координат задается лучом и начало О. На луче откладывают только положительные значения r. Луч вращается вокруг точки О на 360 градусов. ( или на 180 по часовой и на 180 против). Берем первый луч, Он образует угол 0^(o) cos0^(o)=1 r=10*cos0^(0)=10 Откладываем 10 единичных отрезков на луче, который совпадает с осью Ох Второй угол(пи/8) Находим косинус (пи/8) возводим в куб и умножаем на 10. Получаем значение, которое и откладываем на этом луче ( см луч, который подписан как пи/8)

Курсовая работа «Полярная система координат»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

ВВЕДЕНИЕ

Актуальность исследования. Понятие угла и радиуса были известны ещё в первом тысячелетии до нашей эры. Греческим астрономом Гиппархом Никейским , создавшим таблицу, в которой для разных углов приводились длины хорд. Существуют свидетельства применения им полярных координат для определения положения небесных тел. Архимед в своём сочинении «Спирали» описывает так называемую спираль Архимеда, функцию, радиус которой зависит от угла. Работы греческих исследователей, однако, не развились в целостное определение системы координат.

В основе аналитической геометрии лежит возможность однозначного описания точек при помощи наборов чисел, называемых координатами. Описание множества, с помощью соотношений между координатами входящих в него точек, позволяет привлечь для него исследования алгебраические методы, что значительно расширяет возможности анализа. Таким образом, возникает связь между алгеброй и геометрией, ее роль выполняет система координат.

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.

Объект исследования: система координат.

Предмет исследования: полярная система координат.

Цель исследования: разобрать приемы и методы решения задач с применением полярной системы координат.

Исходя из поставленной цели, сформулированы следующие задачи исследования:

Изучить и проанализировать теоретический материал полярной системы координат;

рассмотреть примеры линий, заданных в полярной системе координат.

Курсовая работа состоит из введения, четырёх глав, заключения и списка используемой литературы.

Во введении сформулированы основные характеристики исследования: цель, задачи, объект и предмет исследования. В §1 рассмотрены основные определения полярной системы координат. В §2 описана связь между полярной системой координат и прямоугольной декартовой системой координат . В §3 представлено полярное уравнение прямой и его примеры. В §4 разобраны примеры линий, заданных в полярной системе координат. В заключении сформулированы основные результаты и выводы проведенного исследования. Список литературы содержит 8 наименований.

1. Определение полярной системы координат

Положение точки на плоскости может быть задано не только декартовыми прямоугольными координатами, но и другими способами.

Довольно часто применяется так называемая полярная система координат. Полярная система координат определяется заданием точки , которая называется полюсом, луча , который выходит из этой точки и называется полярной осью, а также масштаба для измерения длин. [1, с. 47]

Пусть — произвольная точка плоскости (Рисунок 1). Обозначим через расстояние от точки до полюса и через  угол, который будем отсчитывать от полярной оси против часовой стрелки.

Числа и называются полярными координатами точки относительно заданной системы: — полярный радиус (первая координата); — полярный угол (вторая координата). По определению величина положительная. Задание полярного радиуса и полярного угла определяет положение точки на плоскости единственным образом.

Если же надо указать полярные координаты какой-нибудь точки на плоскости, то ей будет соответствовать единственное значение полярного радиуса  и бесконечное множество значений полярного угла, т. е. полярный угол определяется неоднозначно: , где ( Z).

Среди возможных значений полярного угла точки М выделяют одно определенное значение угла , которое удовлетворяет неравенствам: (или ). Ограничение изменения угла дает возможность на практике для каждой точки плоскости указать также однозначно ее полярные координаты.

Пример 1.1. [4, с. 23] Построить точки, заданные полярными координатами:

Решение: Построим точку Введем Полярную систему координат. Из точки Проведем луч под углом = к Полярной оси и отметим на нем точку В с координатой = 3. Получаем искомую точку В. Остальные точки строятся аналогично.

Можно сказать, что в качестве главного значения полярного угла берется угол, на котором нужно повернуть луч до совмещения с лучом , но делая при этом поворот не более чем на 180 0 в ту или другую сторону. Исключение составляет только полюс , для которого , а угол не имеет определенного значения.

Порядок построения: на плоскости указать точку (полюс) и луч , который выходит из точки (полярная ось); указать единицу длины. После этого от луча , отложить заданный угол и построить луч , на котором, используя масштаб, указать точку так, чтобы длина отрезка соответствовала первой координате точки. Построение точек показано на рисунке 2.

Пример 1.2. [5, с. 23] Вывести формулу для вычисления площади треугольника , вершина O которого совпадает с полюсом, а две другие даны полярными координатами: , (). Пользуясь этой формулой, вычислить площадь треугольника, одна из вершин которого помещается в полюсе, а две другие имеют полярные координаты: ).

Решение: В треугольнике : ( Рисунок 3). По теореме синусов: =

Используя эту формулу, в частности, получим, что

Пример 1.3. [5, с. 24] Вывести формулу для вычисления расстояния между двумя точками и (), которые заданы полярными координатами. Пользуясь этой формулой, найти расстояние между точками ).

Решение: В треугольнике : ( Рисунок 3). По теореме косинусов:

Воспользовавшись этой формулой, определим расстояние между точками и ). .