Если плоскости параллельны то уравнения плоскостей

Параллельные плоскости, признак и условия параллельности плоскостей.

Эта статья посвящена параллельным плоскостям и параллельности плоскостей. Сначала дано определение параллельных плоскостей, введены обозначения, приведены примеры и графические иллюстрации. Далее приведен признак параллельности плоскостей и теоремы, позволяющие доказывать параллельность плоскостей. В заключении рассмотрены необходимые и достаточные условия параллельности плоскостей, которые заданы в прямоугольной системе координат в трехмерном пространстве, а также подробно разобраны решения примеров.

Навигация по странице.

Параллельные плоскости – основные сведения.

Дадим определение параллельных плоскостей.

Две плоскости называются параллельными, если они не имеют общих точек.

Для обозначения параллельности используется символ «». Таким образом, если плоскости и параллельны, то можно кратко записать .

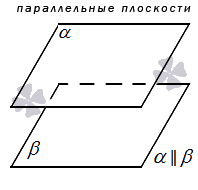
Обычно две параллельные плоскости на чертеже изображаются в виде одинаковых параллелограммов, смещенных относительно друг друга.

Отметим, что если плоскости и параллельны, то также можно сказать, что плоскость параллельна плоскости , или плоскость параллельна плоскости .

Представление о параллельных плоскостях позволяют получить, к примеру, плоскость потолка и пола. Противоположные грани куба лежат в параллельных плоскостях.

Параллельность плоскостей — признак и условия параллельности.

При решении геометрических задач часто встает вопрос: «параллельны ли две заданные плоскости»? Для ответа на него существует признак параллельности плоскостей, который представляет собой достаточное условие параллельности плоскостей. Сформулируем его в виде теоремы.

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны.

С доказательством этого признака параллельности плоскостей Вы можете ознакомиться на страницах учебника геометрии за 10 — 11 классы, который указан в конце статьи в списке рекомендованной литературы.

На практике для доказательства параллельности плоскостей также часто используются две следующие теоремы.

Если одна из двух параллельных плоскостей параллельна третьей плоскости, то другая плоскость либо тоже параллельна этой плоскости, либо совпадает с ней.

Если две несовпадающие плоскости перпендикулярны некоторой прямой, то они параллельны.

На основании приведенных теорем и признака параллельности плоскостей доказывается параллельность любых двух плоскостей.

Теперь подробно остановимся на необходимом и достаточном условии параллельности двух плоскостей и , которые заданы в прямоугольной системе координат в трехмерном пространстве.

Пусть в прямоугольной системе координат Oxyz плоскости соответствует общее уравнение плоскости вида , а плоскости — вида . (Если плоскости заданы уравнениями плоскостей в отрезках, то от них легко перейти к общим уравнениям плоскостей.)

Для параллельности плоскостей и необходимо и достаточно, чтобы система линейных уравнений вида не имела решений (была несовместна).

Если плоскости и параллельны, то по определению они не имеют общих точек. Следовательно, не существует ни одной точки в прямоугольной системе координат Oxyz в трехмерном пространстве, координаты которой удовлетворяли бы одновременно обоим уравнениям плоскостей. Поэтому, система уравнений не имеет решений.

Если система линейных уравнений не имеет решений, то не существует ни одной точки в прямоугольной системе координат Oxyz в трехмерном пространстве, координаты которой удовлетворяют одновременно обоим уравнениям системы. Следовательно, плоскости и не имеют ни одной общей точки, то есть, они параллельны.

Рассмотрим применение необходимого и достаточного условия параллельности плоскостей.

Параллельны ли плоскости и ?

Составим систему уравнений из заданных уравнений плоскостей. Она имеет вид . Выясним, имеет ли эта система линейных уравнений решения (при необходимости смотрите статью решение систем линейных алгебраических уравнений).

Ранг матрицы равен одному, так как все миноры второго порядка равны нулю. Ранг матрицы равен двум, так как минор отличен от нуля. Итак, ранг основной матрицы системы уравнений меньше ранга расширенной матрицы системы. При этом из теоремы Кронекера-Капелли следует, что система уравнений не имеет решений. Этим доказано, что плоскости и параллельны.

Заметим, что использование метода Гаусса для решения системы линейных уравнений привело бы нас к этому же результату.

Необходимое и достаточное условие параллельности плоскостей можно сформулировать иначе.

Для параллельности двух несовпадающих плоскостей и необходимо и достаточно, чтобы нормальный вектор плоскости и нормальный вектор плоскости были коллинеарны.

Доказательство этого условия основано на определении нормального вектора плоскости.

Пусть и — нормальные векторы плоскостей и соответственно. Условие коллинеарности векторов и записывается как , где t – некоторое действительное число.

Таким образом, для параллельности несовпадающих плоскостей и , нормальными векторами которых являются векторы и соответственно, необходимо и достаточно, чтобы существовало действительное число t , для которого справедливо равенство .

Известно, что в прямоугольной системе координат Oxyz в трехмерном пространстве плоскость проходит через три точки , а плоскость определяется уравнением . Докажите параллельность плоскостей и .

Сначала убедимся, что плоскости и не совпадают. Это действительно так, так как координаты точки А не удовлетворяют уравнению плоскости .

Теперь найдем координаты нормальных векторов и плоскостей и и проверим выполнение условия коллинеарности векторов и .

В качестве вектора можно взять векторное произведение векторов и . Векторы и имеют координаты и соответственно (при необходимости смотрите статью нахождение координат вектора по координатам точек его начала и конца). Тогда .

Чтобы определить координаты нормального вектора плоскости приведем ее уравнение к общему уравнению плоскости: . Теперь видно, что .

Проверим выполнение условия коллинеарности векторов и .

Так как , то векторы и связаны равенством , то есть, они коллинеарны.

Итак, плоскости и не совпадают, а их нормальные векторы коллинеарны, следовательно, плоскости и параллельны.

Замечание: разобранное необходимое и достаточное условие не очень удобно для доказательства параллельности плоскостей, так как отдельно приходится доказывать, что плоскости не совпадают.

Параллельные плоскости, признак и условия параллельности плоскостей

В данной статье будут изучены вопросы параллельности плоскостей. Дадим определение плоскостям, которые параллельны между собой; обозначим признаки и достаточные условия параллельности; рассмотрим теорию на иллюстрациях и практических примерах.

Параллельные плоскости: основные сведения

Параллельные плоскости – плоскости, не имеющие общих точек.

Чтобы обозначить параллельность применяют такой символ: ∥ . Если заданы две плоскости: α и β , являющиеся параллельными, краткая запись об этом будет выглядеть так: α ‖ β .

На чертеже, как правило, плоскости, параллельные друг другу, отображаются как два равных параллелограмма, имеющих смещение относительно друг друга.

В речи параллельность можно обозначить так: плоскости α и β параллельны, а также – плоскость α параллельна плоскости β или плоскость β параллельна плоскости α .

Параллельность плоскостей: признак и условия параллельности

В процессе решения геометрических задач зачастую возникает вопрос: а параллельны ли заданные плоскости между собой? Для получения ответа на этот вопрос используют признак параллельности, который также является достаточным условием параллельности плоскостей. Запишем его как теорему.

Плоскости являются параллельными, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Доказательство этой теоремы приводится в программе геометрии за 10 — 11 класс.

В практике для доказательства параллельности, в том числе, применяют две следующие теоремы.

Если одна из параллельных плоскостей параллельна третьей плоскости, то другая плоскость или также параллельна этой плоскости, или совпадает с ней.

Если две несовпадающие плоскости перпендикулярны некоторой прямой, то они параллельны.

На основе этих теорем и самого признака параллельности доказывается факт параллельности любых двух плоскостей.

Рассмотрим подробнее необходимое и достаточное условие параллельности плоскостей α и β , заданных в прямоугольной системе координат трехмерного пространства.

Допустим, что в некоторой прямоугольной системе координат задана плоскость α, которой соответствует общее уравнение A 1 x + B 1 y + C 1 z + D 1 = 0 , а также задана плоскость β , которую определяет общее уравнение вида A 2 x + B 2 y + C 2 z + D 2 = 0 .

Для параллельности заданных плоскостей α и β необходимо и достаточно, чтобы система линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имела решения (являлась несовместной).

Предположим, что заданные плоскости, определяемые уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 являются параллельными, а значит не имеют общих точек. Таким образом, не существует ни одной точки в прямоугольной системе координат трехмерного пространства, координаты которой отвечали бы условиям одновременно обоих уравнений плоскостей, т.е. система A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имеет решения. Если указанная система не имеет решений, тогда не существует ни одной точки в прямоугольной системе координат трехмерного пространства, чьи координаты одновременно отвечали бы условиям обоих уравнений системы. Следовательно, плоскости, заданные уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 не имеют ни одной общей точки, т.е. они параллельны.

Разберем использование необходимого и достаточного условия параллельности плоскостей.

Заданы две плоскости: 2 x + 3 y + z — 1 = 0 и 2 3 x + y + 1 3 z + 4 = 0 . Необходимо определить, являются ли они параллельными.

Решение

Запишем систему уравнений из заданных условий:

2 x + 3 y + z — 1 = 0 2 3 x + y + 1 3 z + 4 = 0

Проверим, возможно ли решить полученную систему линейных уравнений.

Ранг матрицы 2 3 1 2 3 1 1 3 равен одному, поскольку миноры второго порядка равны нулю. Ранг матрицы 2 3 1 1 2 3 1 1 3 — 4 равен двум, поскольку минор 2 1 2 3 — 4 отличен от нуля. Таким образом, ранг основной матрицы системы уравнений меньше, чем ранг расширенной матрицы системы.

Совместно с этим, из теоремы Кронекера-Капелли следует: система уравнений 2 x + 3 y + z — 1 = 0 2 3 x + y + 1 3 z + 4 = 0 не имеет решений. Этим фактом доказывается, что плоскости 2 x + 3 y + z — 1 = 0 и 2 3 x + y + 1 3 z + 4 = 0 являются параллельными.

Отметим, что, если бы мы применили для решения системы линейных уравнений метод Гаусса, это дало бы тот же результат.

Ответ: заданные плоскости параллельны.

Необходимое и достаточное условие параллельности плоскостей возможно описать по-другому.

Чтобы две несовпадающие плоскости α и β были параллельны друг другу необходимо и достаточно, чтобы нормальные векторы плоскостей α и β являлись коллинеарными.

Доказательство сформулированного условия базируется на определении нормального вектора плоскости.

Допустим, что n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) являются нормальными векторами плоскостей α и β соответственно. Запишем условие коллинеарности данных векторов:

n 1 → = t · n 2 ⇀ ⇔ A 1 = t · A 2 B 1 = t · B 2 C 1 = t · C 2 , где t – некое действительное число.

Таким образом, чтобы несовпадающие плоскости α и β с заданными выше нормальными векторами были параллельны, необходимо и достаточно, чтобы имело место действительное число t , для которого верно равенство:

n 1 → = t · n 2 ⇀ ⇔ A 1 = t · A 2 B 1 = t · B 2 C 1 = t · C 2

В прямоугольной системе координат трехмерного пространства заданы плоскости α и β . Плоскость α проходит через точки: A ( 0 , 1 , 0 ) , B ( — 3 , 1 , 1 ) , C ( — 2 , 2 , — 2 ) . Плоскость β описывается уравнением x 12 + y 3 2 + z 4 = 1 Необходимо доказать параллельность заданных плоскостей.

Решение

Удостоверимся, что заданные плоскости не совпадают. Действительно, так и есть, поскольку координаты точки A не соответствуют уравнению плоскости β .

Следующим шагом определим координаты нормальных векторов n 1 → и n 2 → , соответствующие плоскостям α и β . Также проверим условие коллинеарности этих векторов.

Вектор n 1 → можно задать, взяв векторное произведение векторов A B → и A C → . Их координаты соответственно: ( — 3 , 0 , 1 ) и ( — 2 , 2 , — 2 ) . Тогда:

n 1 → = A B → × A C → = i → j → k → — 3 0 1 — 2 1 — 2 = — i → — 8 j → — 3 k → ⇔ n 1 → = ( — 1 , — 8 , — 3 )

Для получения координат нормального вектора плоскости x 12 + y 3 2 + z 4 = 1 приведем это уравнение к общему уравнению плоскости:

x 12 + y 3 2 + z 4 = 1 ⇔ 1 12 x + 2 3 y + 1 4 z — 1 = 0

Таким образом: n 2 → = 1 12 , 2 3 , 1 4 .

Осуществим проверку, выполняется ли условие коллинеарности векторов n 1 → = ( — 1 , — 8 , — 3 ) и n 2 → = 1 12 , 2 3 , 1 4

Так как — 1 = t · 1 12 — 8 = t · 2 3 — 3 = t · 1 4 ⇔ t = — 12 , то векторы n 1 → и n 2 → связаны равенством n 1 → = — 12 · n 2 → , т.е. являются коллинеарными.

Ответ: плоскости α и β не совпадают; их нормальные векторы коллинеарные. Таким образом, плоскости α и β параллельны.

Параллельность плоскостей: признаки и свойства

Две плоскости параллельны, если они не имеют общих точек.

Это определение. Однако в практических целях чаще используется признак параллельности плоскостей:

Плоскости параллельны друг другу, если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости.

Свойства параллельных плоскостей:

1. Если две плоскости параллельны третьей, то они параллельны друг другу.
2. Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
3. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.