Если производная равна бесконечности то уравнение касательной

Геометрический смысл производной

Геометрический смысл производной
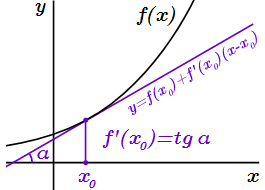
1. Если существует конечная производная функции в точке , то она равна тангенсу угла между осью абсцисс x и наклонной касательной, проведенной к графику функции в точке . При этом угол считается положительным, если график касательной возрастает; угол отрицательный – если убывает. Другими словами, производная функции в точке равна угловому коэффициенту касательной графика функции в точке , а уравнение касательной имеет вид:
.
2. Если производная функции в точке равна бесконечности: , то в этой точке график имеет вертикальную касательную, описываемую уравнением
.

Исследование геометрического смысла производной

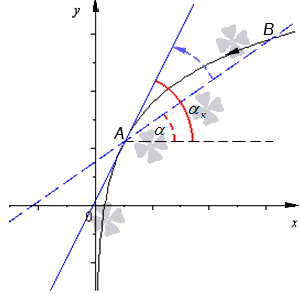
Исследуем геометрический смысл производной функции при некотором, заранее заданном значении аргумента . Считаем, что функция имеет конечную производную в . Тогда существует окрестность точки , в которой функция определена и имеет конечные значения. Проводим оси координат. По оси абсцисс будем откладывать значения переменной x ; по оси ординат – значения переменной y . Строим график функции в окрестности точки .

Отмечаем точку , где . Выбираем на графике произвольную точку , где .

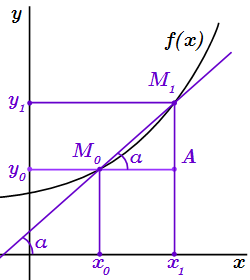
Тангенс угла наклона секущей равен отношению приращения функции к приращению ее аргумента.

Проводим через и секущую . Далее через проводим прямую, параллельную оси x , а через – параллельную оси y . Точку пересечения этих прямых обозначим как A .

Треугольник – прямоугольный. Пусть α – угол между сторонами и . Тогда
.
Но . Отсюда
(1) .
Поскольку прямая параллельна оси x , то угол α является углом между секущей и осью абсцисс x .

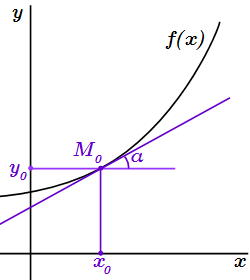
Производная функции в x ₀ равна тангенсу угла наклона касательной к оси абсцисс: f′ ( x ₀) = tg α .

Теперь выполним предельный переход . При этом точка будет стремиться к , приближаясь к ней сколь угодно близко. Сама секущая также будет меняться, поворачиваясь вокруг точки . При она будет стремиться к некоторой предельной прямой, которую мы назовем касательной к графику в точке . Угол наклона α касательной мы найдем из (1), устремляя , и воспользовавшись определением производной:
.
Таким образом, производная функции в точке равна тангенсу угла между касательной, проведенной через эту точку, и осью абсцисс.

Как известно из аналитической геометрии, уравнение прямой с угловым коэффициентом , и проходящей через точку имеет вид:
.
Подставляя , получаем уравнение касательной к графику в точке :
.

Определение касательной

Выше мы провели исследование, и пришли к новому геометрическому объекту – прямой, к которой стремятся секущие при устремлении к . Мы назвали этот объект касательной к графику. В классической геометрии такого объекта нет. Он появляется только в результате применения методов математического анализа. Поэтому мы должны дать его четкое математическое определение.

Касательная к графику функции Пусть точки и принадлежат графику функции . Проведем через них секущую . Касательной к графику функции в точке называется прямая, уравнение которой получается из уравнения секущей при стремящемся к .
Наклонная касательная – это касательная, угол α которой с осью абсцисс заключен в интервале . Уравнение наклонной касательной имеет вид:
,
где – угловой коэффициент – действительное число.
Вертикальная касательная – это касательная, параллельная оси ординат. Уравнение вертикальной касательной имеет вид:
.
Секущая – это прямая, которая пересекает кривую как минимум в двух точках.

Теорема о геометрическом смысле производной

1. Если существует конечная производная функции в точке , то она равна тангенсу угла между осью абсцисс x и наклонной касательной, проведенной к графику функции в точке . При этом угол считается положительным, если график касательной возрастает; угол отрицательный – если убывает. Другими словами, производная функции в точке равна угловому коэффициенту касательной графика функции в точке , а уравнение касательной имеет вид:
.
2. Если производная функции в точке равна бесконечности: , то в этой точке график имеет вертикальную касательную, описываемую уравнением
.

Возьмем на графике функции произвольную точку , отличную от . Здесь . Проведем через точки и прямую, которая является секущей. Составим уравнение прямой, проходящей через эти точки. В наиболее общей форме оно имеет следующий вид:
(Т1) .

Выполняем предельный переход .

1. Пусть в точке существует конечная производная функции.
Перепишем уравнение (Т1) в эквивалентном виде учитывая, что :
.
Считаем, что x и постоянные, то есть заранее заданные числа. Выполняем предельный переход , применяя определение производной:
;
(Т2) .

Мы видим, что при , график секущей (Т1) преобразуется в прямую (Т2), которая является касательной по приведенному выше определению. Как видно из (Т2), касательная является прямой, проходящей через точку с угловым коэффициентом, равным производной функции в . Из аналитической геометрии известно, что угловой коэффициент прямой равен тангенсу угла α между осью абсцисс и этой прямой. Тогда:
.

2. Пусть в точке производная функции равна бесконечности: .

Чтобы разделить уравнение (Т1) на покажем, что существует такая проколотая окрестность точки , в которой
при .
Введем обозначение: . Тогда
.
Согласно определению бесконечного предела функции это означает, что для любого числа M существует такая проколотая окрестность точки , в которой . Возьмем . Тогда существует проколотая окрестность , в которой , то есть в этой окрестности . Поскольку , то отсюда .

Далее рассматриваем в окрестности точки , на которой или, что тоже самое, . Перепишем уравнение (Т1) в эквивалентном виде учитывая, что :
.
Считаем, что y и постоянные. Выполняем предельный переход . По условию, . Применяем свойства бесконечно больших функций:
.

Тем самым мы нашли, что если , то касательная имеет вид
.
Это уравнение прямой, проходящей через точку параллельно оси ординат.

Производная равна бесконечности

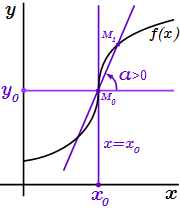
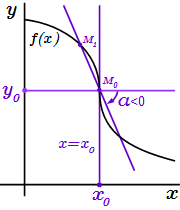
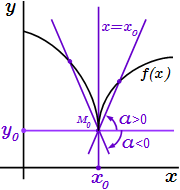
Если производная в равна бесконечности, то касательная вертикальна, но возможны три случая: 1) Производная равна плюс бесконечности: ; 2) производная равна минус бесконечности: ; 3) производная равна бесконечности без определенного знака: .

1) Если производная равна плюс бесконечности: , то угол между осью абсцисс и любой секущей, проходящей через точку положителен: , и стремится к при . Здесь подразумевается, что вторая точка графика , через которую проходит секущая, расположена достаточно близко к .

2) Если производная равна минус бесконечности: , то угол между осью абсцисс и любой секущей, проходящей через точку отрицателен: , и стремится к при .

3) Если производная равна бесконечности без определенного знака: , то углы наклона секущих, проходящих через вторую точку слева и справа от , имеют разные знаки.

Автор: Олег Одинцов . Опубликовано: 22-04-2021

Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной

Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.

Определения и понятия

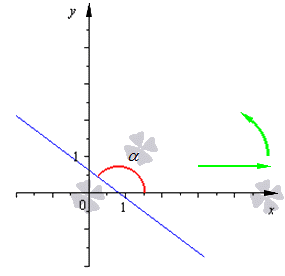
Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.

На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.

Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .

Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .

Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 α π 2 или 0 ° α 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α > 0 , причем имеется возрастание графика.
Если α = π 2 , тогда расположение прямой перпендикулярно о х . Равенство задается при помощи равенства x = c со значением с , являющимся действительным числом.
Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2 α π или 90 ° α 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Определение 3

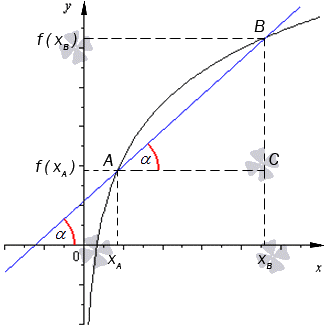
Секущей называют прямую, которая проходит через 2 точки функции f ( x ) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.

По рисунку видно, что А В является секущей, а f ( x ) – черная кривая, α — красная дуга, означающая угол наклона секущей.

Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.

Получаем формулу для нахождения секущей вида:

k = t g α = B C A C = f ( x B ) — f x A x B — x A , где абсциссами точек А и В являются значения x A , x B , а f ( x A ) , f ( x B ) — это значения функции в этих точках.

Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f ( x B ) — f ( x A ) x B — x A или k = f ( x A ) — f ( x B ) x A — x B , причем уравнение необходимо записать как y = f ( x B ) — f ( x A ) x B — x A · x — x A + f ( x A ) или
y = f ( x A ) — f ( x B ) x A — x B · x — x B + f ( x B ) .

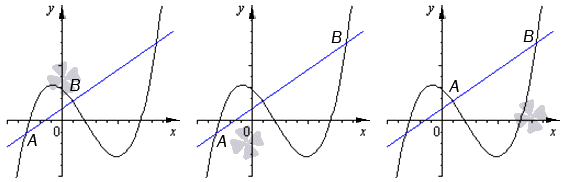
Секущая делит график визуально на 3 части: слева от точки А , от А до В , справа от В . На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.

По определению видно, что прямая и ее секущая в данном случае совпадают.

Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.

Касательная к графику функции f ( x ) в точке x 0 ; f ( x 0 ) называется прямая, проходящая через заданную точку x 0 ; f ( x 0 ) , с наличием отрезка, который имеет множество значений х , близких к x 0 .

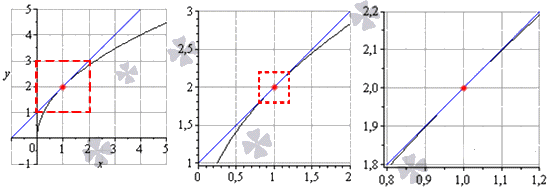
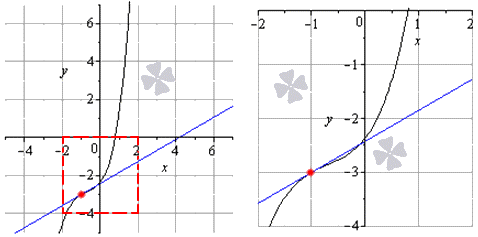
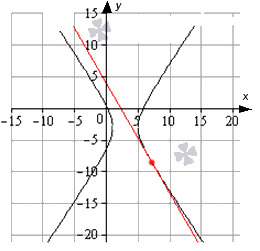
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами ( 1 ; 2 ) . Для наглядности, необходимо рассмотреть графики с приближенными к ( 1 ; 2 ) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.

Очевидно, что y = 2 x сливается с прямой у = х + 1 .

Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А . Для наглядности приведем рисунок.

Секущая А В , обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .

Касательной к графику функции y = f ( x ) в точке А считается предельное положение секущей А В при В стремящейся к А , то есть B → A .

Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.

Геометрический смысл производной функции в точке

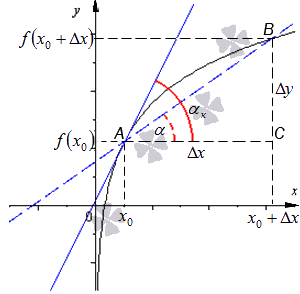
Перейдем к рассмотрению секущей А В для функции f ( x ) , где А и В с координатами x 0 , f ( x 0 ) и x 0 + ∆ x , f ( x 0 + ∆ x ) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f ( x ) = f ( x 0 + ∆ x ) — f ( ∆ x ) . Для наглядности приведем в пример рисунок.

Рассмотрим полученный прямоугольный треугольник А В С . Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f ( x ) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x .

Отсюда следует, что f ‘ ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.

То есть получаем, что f ’ ( x ) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 ( x 0 ) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f ‘ ( x 0 ) .

Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.

Уравнение касательной прямой

Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.

Уравнение касательной к графику функции y = f ( x ) в точке x 0 , f 0 ( x 0 ) принимает вид y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) .

Имеется в виду, что конечным значением производной f ‘ ( x 0 ) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f ‘ ( x ) = ∞ и lim x → x 0 — 0 f ‘ ( x ) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f ‘ ( x ) ≠ lim x → x 0 — 0 f ‘ ( x ) .

Расположение касательной зависит от значения ее углового коэффициента k x = f ‘ ( x 0 ) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у — k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x 0 .

Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 в точке с координатами ( 1 ; 3 ) с определением угла наклона.

Решение

По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, ( 1 ; 3 ) является точкой касания, тогда x 0 = — 1 , f ( x 0 ) = — 3 .

Необходимо найти производную в точке со значением — 1 . Получаем, что

y ‘ = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 ‘ = = e x + 1 ‘ + x 3 3 ‘ — 6 — 3 3 x ‘ — 17 — 3 3 ‘ = e x + 1 + x 2 — 6 — 3 3 y ‘ ( x 0 ) = y ‘ ( — 1 ) = e — 1 + 1 + — 1 2 — 6 — 3 3 = 3 3

Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.

Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3

Отсюда следует, что α x = a r c t g 3 3 = π 6

Ответ: уравнение касательной приобретает вид

y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) y = 3 3 ( x + 1 ) — 3 y = 3 3 x — 9 — 3 3

Для наглядности приведем пример в графической иллюстрации.

Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.

Выяснить наличие существования касательной к графику заданной функции
y = 3 · x — 1 5 + 1 в точке с координатами ( 1 ; 1 ) . Составить уравнение и определить угол наклона.

Решение

По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.

Перейдем к нахождению производной

y ‘ = 3 · x — 1 5 + 1 ‘ = 3 · 1 5 · ( x — 1 ) 1 5 — 1 = 3 5 · 1 ( x — 1 ) 4 5

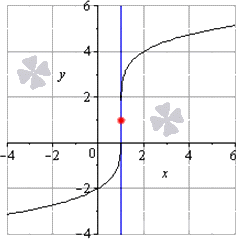
Если x 0 = 1 , тогда f ’ ( x ) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( + 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 — 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( — 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке ( 1 ; 1 ) .

Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .

Для наглядности изобразим графически.

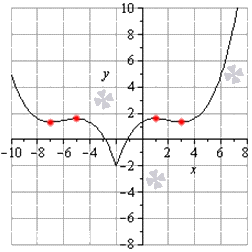
Найти точки графика функции y = 1 15 x + 2 3 — 4 5 x 2 — 16 5 x — 26 5 + 3 x + 2 , где

Касательная не существует;
Касательная располагается параллельно о х ;
Касательная параллельна прямой y = 8 5 x + 4 .

Решение

Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ — ∞ ; 2 и [ — 2 ; + ∞ ) . Получаем, что

y = — 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 , x ∈ [ — 2 ; + ∞ )

Необходимо продифференцировать функцию. Имеем, что

y ‘ = — 1 15 x 3 + 18 x 2 + 105 x + 176 ‘ , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 ‘ , x ∈ [ — 2 ; + ∞ ) ⇔ y ‘ = — 1 5 ( x 2 + 12 x + 35 ) , x ∈ — ∞ ; — 2 1 5 x 2 — 4 x + 3 , x ∈ [ — 2 ; + ∞ )

Когда х = — 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:

lim x → — 2 — 0 y ‘ ( x ) = lim x → — 2 — 0 — 1 5 ( x 2 + 12 x + 35 = — 1 5 ( — 2 ) 2 + 12 ( — 2 ) + 35 = — 3 lim x → — 2 + 0 y ‘ ( x ) = lim x → — 2 + 0 1 5 ( x 2 — 4 x + 3 ) = 1 5 — 2 2 — 4 — 2 + 3 = 3

Вычисляем значение функции в точке х = — 2 , где получаем, что

y ( — 2 ) = 1 15 — 2 + 2 3 — 4 5 ( — 2 ) 2 — 16 5 ( — 2 ) — 26 5 + 3 — 2 + 2 = — 2 , то есть касательная в точке ( — 2 ; — 2 ) не будет существовать.
Касательная параллельна о х , когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f ‘ ( x 0 ) . То есть необходимо найти значения таких х , когда производная функции обращает ее в ноль. То есть значения f ’ ( x ) и будут являться точками касания, где касательная является параллельной о х .

Когда x ∈ — ∞ ; — 2 , тогда — 1 5 ( x 2 + 12 x + 35 ) = 0 , а при x ∈ ( — 2 ; + ∞ ) получаем 1 5 ( x 2 — 4 x + 3 ) = 0 .

— 1 5 ( x 2 + 12 x + 35 ) = 0 D = 12 2 — 4 · 35 = 144 — 140 = 4 x 1 = — 12 + 4 2 = — 5 ∈ — ∞ ; — 2 x 2 = — 12 — 4 2 = — 7 ∈ — ∞ ; — 2 1 5 ( x 2 — 4 x + 3 ) = 0 D = 4 2 — 4 · 3 = 4 x 3 = 4 — 4 2 = 1 ∈ — 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ — 2 ; + ∞

Вычисляем соответствующие значения функции

y 1 = y — 5 = 1 15 — 5 + 2 3 — 4 5 — 5 2 — 16 5 — 5 — 26 5 + 3 — 5 + 2 = 8 5 y 2 = y ( — 7 ) = 1 15 — 7 + 2 3 — 4 5 ( — 7 ) 2 — 16 5 — 7 — 26 5 + 3 — 7 + 2 = 4 3 y 3 = y ( 1 ) = 1 15 1 + 2 3 — 4 5 · 1 2 — 16 5 · 1 — 26 5 + 3 1 + 2 = 8 5 y 4 = y ( 3 ) = 1 15 3 + 2 3 — 4 5 · 3 2 — 16 5 · 3 — 26 5 + 3 3 + 2 = 4 3

Отсюда — 5 ; 8 5 , — 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.

Рассмотрим графическое изображение решения.

Черная линия – график функции, красные точки – точки касания.

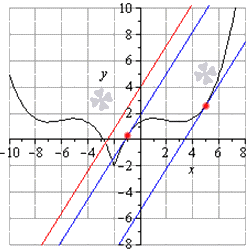
Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y ‘ ( x ) = 8 5 . Тогда, если x ∈ — ∞ ; — 2 , получаем, что — 1 5 ( x 2 + 12 x + 35 ) = 8 5 , а если x ∈ ( — 2 ; + ∞ ) , тогда 1 5 ( x 2 — 4 x + 3 ) = 8 5 .

Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что

— 1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 — 4 · 43 = — 28 0

Другое уравнение имеет два действительных корня, тогда

1 5 ( x 2 — 4 x + 3 ) = 8 5 x 2 — 4 x — 5 = 0 D = 4 2 — 4 · ( — 5 ) = 36 x 1 = 4 — 36 2 = — 1 ∈ — 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ — 2 ; + ∞

Перейдем к нахождению значений функции. Получаем, что

y 1 = y ( — 1 ) = 1 15 — 1 + 2 3 — 4 5 ( — 1 ) 2 — 16 5 ( — 1 ) — 26 5 + 3 — 1 + 2 = 4 15 y 2 = y ( 5 ) = 1 15 5 + 2 3 — 4 5 · 5 2 — 16 5 · 5 — 26 5 + 3 5 + 2 = 8 3

Точки со значениями — 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .

Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках — 1 ; 4 15 , 5 ; 8 3 .

Возможно существование бесконечного количества касательных для заданных функций.

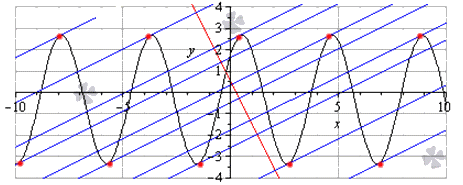
Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x — π 4 — 1 3 , которые располагаются перпендикулярно прямой y = — 2 x + 1 2 .

Решение

Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется — 1 , то есть записывается как k x · k ⊥ = — 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = — 2 , тогда k x = — 1 k ⊥ = — 1 — 2 = 1 2 .

Теперь необходимо найти координаты точек касания. Нужно найти х , после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y ‘ ( x 0 ) . Из данного равенства найдем значения х для точек касания.

y ‘ ( x 0 ) = 3 cos 3 2 x 0 — π 4 — 1 3 ‘ = 3 · — sin 3 2 x 0 — π 4 · 3 2 x 0 — π 4 ‘ = = — 3 · sin 3 2 x 0 — π 4 · 3 2 = — 9 2 · sin 3 2 x 0 — π 4 ⇒ k x = y ‘ ( x 0 ) ⇔ — 9 2 · sin 3 2 x 0 — π 4 = 1 2 ⇒ sin 3 2 x 0 — π 4 = — 1 9

Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.

3 2 x 0 — π 4 = a r c sin — 1 9 + 2 πk или 3 2 x 0 — π 4 = π — a r c sin — 1 9 + 2 πk

3 2 x 0 — π 4 = — a r c sin 1 9 + 2 πk или 3 2 x 0 — π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 — a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z — множество целых чисел.

Найдены х точек касания. Теперь необходимо перейти к поиску значений у :

y 0 = 3 cos 3 2 x 0 — π 4 — 1 3

y 0 = 3 · 1 — sin 2 3 2 x 0 — π 4 — 1 3 или y 0 = 3 · — 1 — sin 2 3 2 x 0 — π 4 — 1 3

y 0 = 3 · 1 — — 1 9 2 — 1 3 или y 0 = 3 · — 1 — — 1 9 2 — 1 3

y 0 = 4 5 — 1 3 или y 0 = — 4 5 + 1 3

Отсюда получаем, что 2 3 π 4 — a r c sin 1 9 + 2 πk ; 4 5 — 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; — 4 5 + 1 3 являются точками касания.

Ответ: необходимы уравнения запишутся как

y = 1 2 x — 2 3 π 4 — a r c sin 1 9 + 2 πk + 4 5 — 1 3 , y = 1 2 x — 2 3 5 π 4 + a r c sin 1 9 + 2 πk — 4 5 + 1 3 , k ∈ Z

Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.

Рисунок показывает, что расположение функции идет на промежутке [ — 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = — 2 x + 1 2 . Красные точки – это точки касания.

Касательная к окружности, эллипсу, гиперболе, параболе

Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.

Касательная к окружности

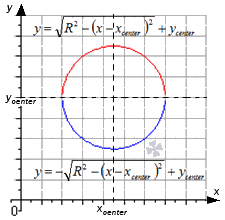
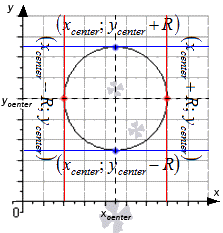
Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x — x c e n t e r 2 + y — y c e n t e r 2 = R 2 .

Данное равенство может быть записано как объединение двух функций:

y = R 2 — x — x c e n t e r 2 + y c e n t e r y = — R 2 — x — x c e n t e r 2 + y c e n t e r

Первая функция располагается вверху, а вторая внизу, как показано на рисунке.

Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 — x — x c e n t e r 2 + y c e n t e r или y = — R 2 — x — x c e n t e r 2 + y c e n t e r в указанной точке.

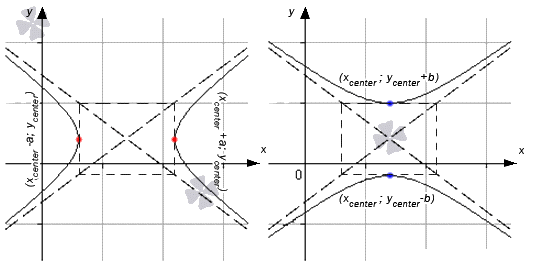
Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r — R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r — R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r — R ; y c e n t e r будут являться параллельными о у , тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r — R .

Касательная к эллипсу

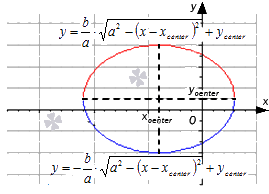
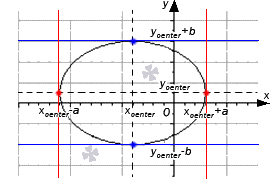
Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x — x c e n t e r 2 a 2 + y — y c e n t e r 2 b 2 = 1 .

Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что

y = b a · a 2 — ( x — x c e n t e r ) 2 + y c e n t e r y = — b a · a 2 — ( x — x c e n t e r ) 2 + y c e n t e r

Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у . Ниже для наглядности рассмотрим рисунок.

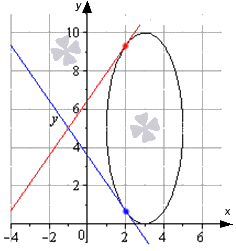
Написать уравнение касательной к эллипсу x — 3 2 4 + y — 5 2 25 = 1 в точках со значениями x равного х = 2 .

Решение

Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что

x — 3 2 4 x = 2 + y — 5 2 25 = 1 1 4 + y — 5 2 25 = 1 ⇒ y — 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5

Тогда 2 ; 5 3 2 + 5 и 2 ; — 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.

Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что

x — 3 2 4 + y — 5 2 25 = 1 y — 5 2 25 = 1 — x — 3 2 4 ( y — 5 ) 2 = 25 · 1 — x — 3 2 4 y — 5 = ± 5 · 1 — x — 3 2 4 y = 5 ± 5 2 4 — x — 3 2

Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 — x — 3 2 , а нижний y = 5 — 5 2 4 — x — 3 2 .

Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид

y ‘ = 5 + 5 2 4 — x — 3 2 ‘ = 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = — 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = — 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = 5 2 3 ( x — 2 ) + 5 3 2 + 5

Получаем, что уравнение второй касательной со значением в точке
2 ; — 5 3 2 + 5 принимает вид

y ‘ = 5 — 5 2 4 — ( x — 3 ) 2 ‘ = — 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = — 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = — 5 2 3 ( x — 2 ) — 5 3 2 + 5

Графически касательные обозначаются так:

Касательная к гиперболе

Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r — α ; y c e n t e r , имеет место задание неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r — b , тогда задается при помощи неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = — 1 .

Гипербола может быть представлена в виде двух объединенных функций вида

y = b a · ( x — x c e n t e r ) 2 — a 2 + y c e n t e r y = — b a · ( x — x c e n t e r ) 2 — a 2 + y c e n t e r или y = b a · ( x — x c e n t e r ) 2 + a 2 + y c e n t e r y = — b a · ( x — x c e n t e r ) 2 + a 2 + y c e n t e r

В первом случае имеем, что касательные параллельны о у , а во втором параллельны о х .

Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.

Составить уравнение касательной к гиперболе x — 3 2 4 — y + 3 2 9 = 1 в точке 7 ; — 3 3 — 3 .

Решение

Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что

x — 3 2 4 — y + 3 2 9 = 1 ⇒ y + 3 2 9 = x — 3 2 4 — 1 ⇒ y + 3 2 = 9 · x — 3 2 4 — 1 ⇒ y + 3 = 3 2 · x — 3 2 — 4 и л и y + 3 = — 3 2 · x — 3 2 — 4 ⇒ y = 3 2 · x — 3 2 — 4 — 3 y = — 3 2 · x — 3 2 — 4 — 3

Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; — 3 3 — 3 .

Очевидно, что для проверки первой функции необходимо y ( 7 ) = 3 2 · ( 7 — 3 ) 2 — 4 — 3 = 3 3 — 3 ≠ — 3 3 — 3 , тогда точка графику не принадлежит, так как равенство не выполняется.

Для второй функции имеем, что y ( 7 ) = — 3 2 · ( 7 — 3 ) 2 — 4 — 3 = — 3 3 — 3 ≠ — 3 3 — 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.

y ‘ = — 3 2 · ( x — 3 ) 2 — 4 — 3 ‘ = — 3 2 · x — 3 ( x — 3 ) 2 — 4 ⇒ k x = y ‘ ( x 0 ) = — 3 2 · x 0 — 3 x 0 — 3 2 — 4 x 0 = 7 = — 3 2 · 7 — 3 7 — 3 2 — 4 = — 3

Ответ: уравнение касательной можно представить как

y = — 3 · x — 7 — 3 3 — 3 = — 3 · x + 4 3 — 3

Наглядно изображается так:

Касательная к параболе

Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y ( x 0 ) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y ‘ ( x 0 ) · x — x 0 + y ( x 0 ) . Такая касательная в вершине параллельна о х .

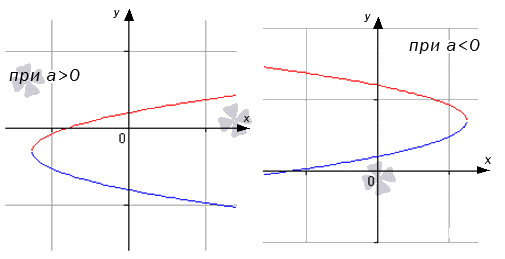
Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у . Получаем, что

x = a y 2 + b y + c ⇔ a y 2 + b y + c — x = 0 D = b 2 — 4 a ( c — x ) y = — b + b 2 — 4 a ( c — x ) 2 a y = — b — b 2 — 4 a ( c — x ) 2 a

Графически изобразим как:

Для выяснения принадлежности точки x 0 , y ( x 0 ) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.

Написать уравнение касательной к графику x — 2 y 2 — 5 y + 3 , когда имеем угол наклона касательной 150 ° .

Решение

Начинаем решение с представления параболы в качестве двух функций. Получим, что

— 2 y 2 — 5 y + 3 — x = 0 D = ( — 5 ) 2 — 4 · ( — 2 ) · ( 3 — x ) = 49 — 8 x y = 5 + 49 — 8 x — 4 y = 5 — 49 — 8 x — 4

Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.

k x = y ‘ ( x 0 ) = t g α x = t g 150 ° = — 1 3

Отсюда определим значение х для точек касания.

Первая функция запишется как

y ‘ = 5 + 49 — 8 x — 4 ‘ = 1 49 — 8 x ⇒ y ‘ ( x 0 ) = 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3

Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.

Вторая функция запишется как

y ‘ = 5 — 49 — 8 x — 4 ‘ = — 1 49 — 8 x ⇒ y ‘ ( x 0 ) = — 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3 x 0 = 23 4 ⇒ y ( x 0 ) = 5 — 49 — 8 · 23 4 — 4 = — 5 + 3 4

Имеем, что точки касания — 23 4 ; — 5 + 3 4 .

Ответ: уравнение касательной принимает вид

Н.С. Шернина, преподаватель Кубанского госуниверситета

1. Производная

Рассмотрим некоторую функцию в двух точках и : и .
Здесь через обозначено некоторое малое изменение аргумента, называемое приращением аргумента; соответственно разность между двумя значениями функции: называется приращением функции.

Если этот предел существует, то функция называется дифференцируемой в точке . Производная функции обозначается (формула 2)

2. Геометрический смысл производной

Рассмотрим график функции .

Из рис.1 видно, что для любых двух точек A и B графика функции можно записать формула 3). В ней — угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует вывод.

3. Уравнение касательной

Выведем уравнение касательной к графику функции в точке . В общем случае уравнение прямой с угловым коэффициентом имеет вид:
Чтобы найти b,воспользуемся тем, что касательная проходит через точку A:
Отсюда следует: .
Подставляя это выражение вместо b, получаем уравнение касательной(формула 4).

4. Механический смысл производной

Рассмотрим простейший случай: движение материальной точки вдоль координатной оси. При этом задан закон движения точки: координата x движущейся точки – это известная функция времени . В течение интервала времени от до точка перемещается на расстояние: .
Её средняя скорость () находится по формуле: . При значение средней скорости стремится к определённой величине, которая в физике называется мгновенной скоростью материальной точки в момент времени . Следовательно, для мгновенной скорости можно записать формулу 5

Если сравнить эту формулу с формулой производной 1, то можно сделать вывод, что

5. Дифференциал и его связь с производной
Дифференциал функции. Геометрический смысл дифференциала

Дифференциал функции – это произведение производной и приращения аргумента (формула 6).

Геометрический смысл дифференциала ясен из рисунка 2.

Здесь . Из можно записать: , где β – угол наклона касательной АС к оси ОХ. Но если , то . Дифференциал CD равен сумме отрезков BС и BD (приращение функции). Но, если , то и отрезок . Значит, дифференциал отличается от производной на бесконечно малую величину.

6. Основные свойства производных и дифференциалов. Производная сложной функции
6.1 Правила дифференцирования функций. Таблица производных простейших элементарных функций.
Если , то , .
Если и — дифференцируемые функции в точке , то можно записать:

Таблица производных простейших элементарных функций

1. ,
где С – постоянное число
2.
Частные случаи:

3.
Частный случай

4.
Частный случай

5.
6.
7.
8.
9.
10.
11.
12.

6.2 Производная сложной функции

Рассмотрим сложную функцию, аргумент которой также является функцией: . Если функция f имеет производную в точке , а функция g имеет производную в точке , то сложная функция h также имеет производную в точке , вычисляемую по формуле:

6.3 Вторая производная

Если производная функции дифференцируема в точке , то её производная называется второй производной функции в точке , и обозначается .

6.4 Правило Лопиталя

Пусть при для функций и, дифференцируемых в некоторой окрестности точки а , выполняются условия. (формулы 7).

Эта теорема называется правилом Лопиталя. Она позволяет вычислять пределы отношения функций, когда и числитель, и знаменатель cтремятся либо к нулю, либо к бесконечности. Правило Лопиталя, как говорят математики, позволяет избавляться от неопределённостей типа: и . Рассмотрите примеры.

При неопределённостях другого типа: , , , , нужно проделать предварительно ряд тождественных преобразований, чтобы привести их к какой-то из двух неопределённостей: либо , либо . После этого можно применять правило Лопиталя. Покажем некоторые из возможных преобразований указанных неопределённостей.

: пусть ,, тогда данная неопределённость приводится к типу посредством следующего преобразования:

: пусть , , тогда данная неопределённость приводится к типу или с помощью преобразований:

остальные неопределённости приводятся к первым двум с помощью логарифмического преобразования:

Если же после применения правила Лопиталя неопределённость типа или осталась, нужно применить его повторно. Многократное применение правила Лопиталя может привести к требуемому результату. Правило Лопиталя применимо и в случае, если .

7. Применение производной в исследовании функций
7.1 Связь между непрерывностью и дифференцируемостью функции

Если функция дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной (рисунок 3). Если же функция разрывная в некоторой точке, то она не имеет производной в этой точке.

7.2 Достаточные признаки монотонности функции

Если в каждой точке интервала , то функция возрастает на этом интервале. Если в каждой точке интервала , то функция убывает на этом интервале.

7.3 Теорема Дарбу

Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак.

Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании.Рассмотрите примеры

Следовательно, функция на рисунке 4а возрастает на интервалах и и убывает на интервале . Точка не входит в область определения функции, но по мере приближения x к 0 слагаемое неограниченно возрастает. Поэтому функция также неограниченно возрастает. В точке значение функции равно 3. В соответствии с этим анализом мы можем построить график функции ( рис.4б ).

7.4 Критические точки

Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции. Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум ( минимум или максимум, рис.5а,б).

В точках , (рис.5a) и (рис.5b) производная равна 0. В точках , (рис.5б) производная не существует. Но все они – это точки экстремума.

7.5 Необходимое условие экстремума

Если — точка экстремума функции и производная существует в этой точке, то .

Эта теорема – необходимое условие экстремума. Если же производная функции в некоторой точке равна 0, то это не значит, что функция всегда имеет экстремум в этой точке. Например, производная функции равна 0 при , но эта функция не имеет экстремум в этой точке ( рис.6 ).
С другой стороны, функция , представленная на рис.3, имеет минимум в точке , но в этой точке производной не существует.

7.6 Достаточные условия экстремума

Если производная при переходе через точку меняет свой знак с плюса на минус, то — точка максимума.
Если производная при переходе через точку меняет свой знак с минуса на плюс, то — точка минимума.

7.7 План исследования функции
Для построения графика функции нужно:

Пример . Исследование функции , построение графика
1) область определения (x – любое действительное число); область значений , так как – многочлен нечётной степени;
2) функция не является ни чётной, ни нечётной (докажите самостоятельно);
3) – непериодическая функция (докажите самостоятельно);
4) график функции пересекается с осью Y в точке , так как .
Чтобы найти нули функции нужно решить уравнение: .
Один из его корней очевиден. Другие корни находятся (если они есть!) из решения квадратного уравнения: . Оно получено делением многочлена на двучлен . Легко проверить, что два других корня: и . Таким образом, нулями функции являются:-2, -1 и 1.

5) Это означает, что числовая ось делится этими корнями на четыре интервала знакопостоянства, внутри которых функция сохраняет свой знак. Этот же результат может быть получен разложением многочлена на множители:
. Затем надо оценить знак произведения методом интервалов.
6) Производная не имеет точек, в которых она не существует, поэтому её область определения R (все действительные числа); нули – это корни уравнения: .
Эти корни: .
Функция имеет две критические точки и три интервала монотонности: .
Полученные результаты сведены в таблицу. В ней стрелками обозначены выводы о возрастании функции или её убывании (наклонная стрелка вверх или вниз) внутри соответствующего интервала.

Теперь мы располагаем полной информацией для построения графика данной функции (рис. 8).

7.8 Выпуклость, вогнутость, точки перегиба

Функция называется выпуклой на интервале , если её график на этом интервале лежит ниже касательной, проведенной к кривой в любой точке , при этом .
Функция называется вогнутой на интервале , если её график на этом интервале лежит выше касательной, проведенной к кривой в любой точке , при этом .

7.9 Достаточное условие вогнутости (выпуклости) функции

Пусть функция дважды дифференцируема (имеет вторую производную) на интервале , тогда: если для любого , то функция является вогнутой на интервале ; если для любого , то функция является выпуклой на интервале .
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба существует вторая производная , то .
Пример : Рассмотрим график функции . Эта функция является вогнутой при и выпуклой при .
В самом деле, , но при и при , следовательно, при и при , откуда следует, что функция является вогнутой при и выпуклой при . Тогда является точкой перегиба функции .