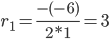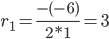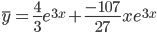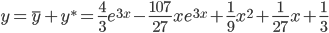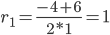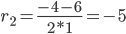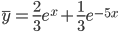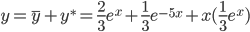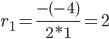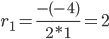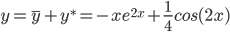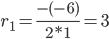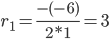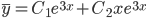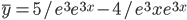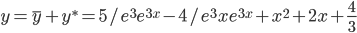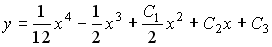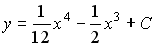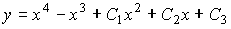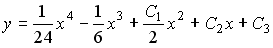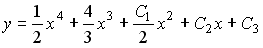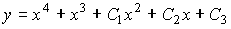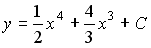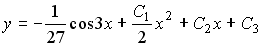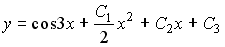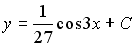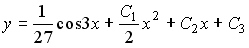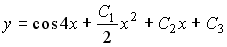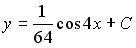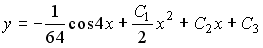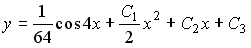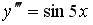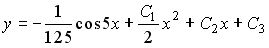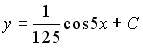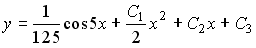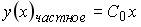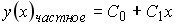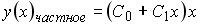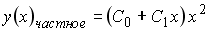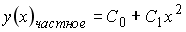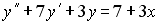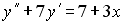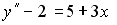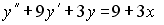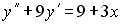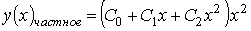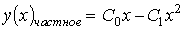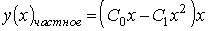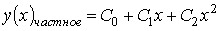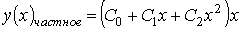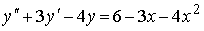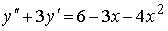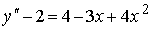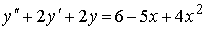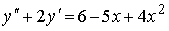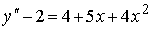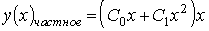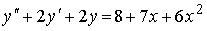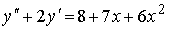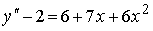Если решение дифференциального уравнения удовлетворяющее условиям тогда равно

Пример решения дифференциального уравнения

Решение находим с помощью сервиса линейные дифференциальные уравнения с постоянными коэффициентами.
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -6 r + 9 = 0
D = (-6) 2 — 4·1·9 = 0


Корни характеристического уравнения:
Корень характеристического уравнения r₁ = 3 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e 3x , y₂ = xe 3x
Общее решение однородного уравнения имеет вид: y = C₁·e 3x +C₂·x·e 3x
Найдем частное решение при условии:y(0) = 4/3, y'(0) = 1/27
Поскольку y(0) = c1, то получаем первое уравнение:
c1 = 4/3
Находим первую производную:
y’ = 3·c1·e 3·x +3·c2·x·e 3·x +c2·e 3·x
Поскольку y'(0) = 3·c1+c2, то получаем второе уравнение:
3·c1+c2 = 1/27
В итоге получаем систему из двух уравнений:
c1 = 4/3
3·c1+c2 = 1/27
т.е.:
c₁ = 4 /₃, c₂ = -107 /₂₇
Тогда частное решение при заданных начальных условиях можно записать в виде:

Рассмотрим правую часть:
f(x) = x 2 -x+3
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = x 2 -x+3, Q(x) = 0, α = 0, β = 0.
Следовательно, число α + βi = 0 + 0i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида: y*=A·x 2 +B·x+C
Вычисляем производные:
y’ = 2·A·x+B
y″ = 2·A
которые подставляем в исходное дифференциальное уравнение:
y″ -6y’ + 9y = (2·A) -6(2·A·x+B) + 9(Ax 2 + Bx + C) = x 2 -x+3
или
9·A·x 2 -12·A·x+2·A+9·B·x-6·B+9·C = x 2 -x+3
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
9A = 1
-12A + 9B = -1
2A -6B + 9C = 3
Решая ее, находим:
A = 1 /₉;B = 1 /₂₇;C = 1 /₃;
Частное решение имеет вид:
y * = 1 /₉x 2 + 1 /₂₇x + 1 /₃
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример №2. y″ +4y’ — 5y = 2·e x

Решение:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 +4 r — 5 = 0
D = 4 2 — 4·1·(-5) = 36


Корни характеристического уравнения:
r₁ = 1
r₂ = -5
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e x
y₂ = e -5x
Общее решение однородного уравнения имеет вид: y = C₁·e 3x +C₂·e -5x
Найдем частное решение при условии:y(0) = 1, y'(0) = -1
Поскольку y(0) = c1+c2, то получаем первое уравнение:
c1+c2 = 1
Находим первую производную:
y’ = c1·e x -5·c2·e -5·x
Поскольку y'(0) = c1-5·c2, то получаем второе уравнение:
c1-5·c2 = -1
В итоге получаем систему из двух уравнений:
c1+c2 = 1
c1-5·c2 = -1
которую решаем или методом матриц или методом исключения переменных.
c₁ = 2 /₃, c₂ = 1 /₃
Тогда частное решение при заданных начальных условиях можно записать в виде:

Рассмотрим правую часть:
f(x) = 2·e x
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 2, Q(x) = 0, α = 1, β = 0.
Следовательно, число α + βi = 1 + 0i является корнем характеристического уравнения кратности k = 1(r₁).
Уравнение имеет частное решение вида: y*=A·x 2 +B·x+C
Вычисляем производные: y’ = A·e x (x+1)
y″ = A·e x (x+2)
которые подставляем в исходное дифференциальное уравнение:
y″ + 4y’ -5y = (A·e x (x+2)) + 4(A·e x (x+1)) -5(x (Ae x )) = 2·e x
или
6·A·e x = 2·e x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
6A = 2
Решая ее, находим:
A = 1 /₃;
Частное решение имеет вид:
y * = x ( 1 /₃e x )
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример №3. y″ — 4y’ + 4y = 2sin(2x), y(0) = 0. y'(0) = -1

Решение:
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -4 r + 4 = 0
D = (-4) 2 — 4·1·4 = 0


Корни характеристического уравнения:
Корень характеристического уравнения r₁ = 2 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e 2x
y₂ = xe 2x
Общее решение однородного уравнения имеет вид: y = C₁·e 2x +C₂·x·e 2x
Найдем частное решение при условии:y(0) = 0, y'(0) = -1
Поскольку y(0) = c1, то получаем первое уравнение:
c1 = 0
Находим первую производную:
y’ = 2·c1·e 2·x +2·c2·x·e 2·x +c2·e 2·x
Поскольку y'(0) = 2·c1+c2, то получаем второе уравнение:
2·c1+c2 = -1
В итоге получаем систему из двух уравнений:
c1 = 0
2·c1+c2 = -1
т.е.:
c₁ = 0, c₂ = -1
Тогда частное решение при заданных начальных условиях можно записать в виде:
y =-x·e 2x
Рассмотрим правую часть: f(x) = 2·sin(2·x)
Поиск частного решения.
Здесь P(x) = 0, Q(x) = 2, α = 0, β = 2.
Следовательно, число α + βi = 0 + 2i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида: y * = Acos(2x) + Bsin(2x)
Вычисляем производные:
y’ = 2·B·cos(2x)-2·A·sin(2x)
y″ = -4(A·cos(2x)+B·sin(2x))
которые подставляем в исходное дифференциальное уравнение:
y″ -4y’ + 4y = (-4(A·cos(2x)+B·sin(2x))) -4(2·B·cos(2x)-2·A·sin(2x)) + 4(Acos(2x) + Bsin(2x)) = 2·sin(2·x)
или
8·A·sin(2x)-8·B·cos(2x) = 2·sin(2·x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
8A = 2
0A -8B = 0
Решая ее, находим:
A = 1 /₄;B = 0;
Частное решение имеет вид:
y * = 1 /₄cos(2x) + 0sin(2x)
или
y * = 1 /₄cos(2x)
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример №4. Найти частное решение, общее решение и решение задачи Коши уравнения: y″ — 6y’ + 9y = 9x 2 +6x + 2, y(1) = 1, y'(1) = -1

Решение:
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -6 r + 9 = 0
D = (-6) 2 — 4·1·9 = 0


Корни характеристического уравнения:
Корень характеристического уравнения r₁ = 3 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e 3x
y₂ = xe 3x
Общее решение однородного уравнения имеет вид:

Найдем частное решение при условии:y(1) = 1, y'(1) = -1
Поскольку y(1) = c1·e 3 +c2·e 3 , то получаем первое уравнение:
c1·e 3 +c2·e 3 = 1
Находим первую производную:
y’ = 3·c1·e 3·x +3·c2·x·e 3·x +c2·e 3·x
Поскольку y'(1) = 3·c1·e 3 +4·c2·e 3 , то получаем второе уравнение:
3·c1·e 3 +4·c2·e 3 = -1
В итоге получаем систему из двух уравнений:
c1·e 3 +c2·e 3 = 1
3·c1·e 3 +4·c2·e 3 = -1
которую решаем или методом матриц или методом исключения переменных.
c₁ = 5/e 3 , c₂ = -4/e 3
Тогда частное решение при заданных начальных условиях можно записать в виде:

Рассмотрим правую часть:
f(x) = 9·x 2 +6·x+2
Поиск частного решения.
Здесь P(x) = 9·x 2 +6·x+2, Q(x) = 0, α = 0, β = 0.
Следовательно, число α + βi = 0 + 0i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида: y*=A·x 2 +B·x+C
Вычисляем производные:
y’ = 2·A·x+B
y″ = 2·A
которые подставляем в исходное дифференциальное уравнение:
y″ -6y’ + 9y = (2·A) -6(2·A·x+B) + 9(Ax 2 + Bx + C) = 9·x 2 +6·x+2
или
9·A·x 2 -12·A·x+2·A+9·B·x-6·B+9·C = 9·x 2 +6·x+2
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
9A = 9
-12A + 9B = 6
2A -6B + 9C = 2
Решая ее, находим:
A = 1;B = 2;C = 4 /₃;
Частное решение имеет вид:
y * = x 2 + 2x + 4 /₃
Таким образом, общее решение дифференциального уравнения имеет вид:

Дифференциальным уравнением первого порядка с разделяющимися переменными

4) линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами

Задание #118

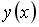
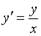
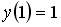
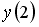
Если — решение уравнения , удовлетворяющее условию , тогда равно …

__________2_________________

Задание #119

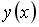
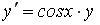
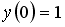
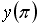
Если — решение уравнения , удовлетворяющее условию , тогда равно …

________1___________________

Задание #120

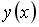
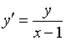
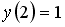
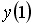
Если — решение уравнения , удовлетворяющее условию , тогда равно …

_________0__________________

Задание #121

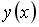
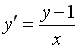
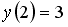
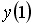
Если — решение уравнения , удовлетворяющее условию , тогда равно …

___________2________________

Задание #122

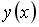
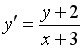
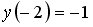
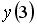
Если — решение уравнения , удовлетворяющее условию , тогда равно …

___________4________________

Задание #123

Общее решение дифференциального уравнения 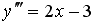имеет вид …

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

Задание #124

Общее решение дифференциального уравнения 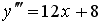имеет вид …

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

Задание #125

Общее решение дифференциального уравнения 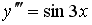имеет вид …

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

Задание #126

Общее решение дифференциального уравнения 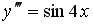имеет вид …

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

Задание #127

Общее решение дифференциального уравнения имеет вид …

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

Задание #128

Установите соответствие между дифференциальным уравнением и общим видом его частного решения

Укажите соответствие для всех 3 вариантов ответа:

1)

2)

3)

4)

5)

_2_

_3_

_4_

Задание #129

Установите соответствие между дифференциальным уравнением и общим видом его частного решения

Укажите соответствие для всех 3 вариантов ответа:

1)

2)

3)

4)

5)

_3_

_2_

_4_

Задание #130

Установите соответствие между дифференциальным уравнением и общим видом его частного решения …

Укажите соответствие для всех 3 вариантов ответа:

1)

2)

3)

4)

5)

_4_

_5_

_1_

Задание #131

Установите соответствие между дифференциальным уравнением и общим видом его частного решения …

Укажите соответствие для всех 3 вариантов ответа:

1)

2)

3)

4)

5)

_2_

_1_

_5_

Задание #132

Установите соответствие между дифференциальным уравнением и общим видом его частного решения …

Укажите соответствие для всех 3 вариантов ответа:

1)

2)

3)

4)

5)

_3_

_4_

_5_

Задание #133

Бросают 2 монеты. События А — «цифра на первой монете» и В — «герб на второй монете» являются:

Выберите один из 4 вариантов ответа:

Решением дифференциального уравнения

Главная > Решение

Дифференциальные уравнения первого порядка

Дифференциальным уравнением называется уравнение, связывающее независимую переменную x, искомую функцию y(x) и производную искомой функции.

Символически дифференциальное уравнение можно написать так

.

Неизвестной здесь является функция y , входящая под знак производных (или дифференциалов).

Если искомая функция y(x) есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным . В этой главе мы будем рассматривать только обыкновенные дифференциальные уравнения.

Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.

Например, уравнение есть уравнение первого порядка,

а уравнение — уравнение второго порядка.

Решением дифференциального уравнения называется всякая функция y(x), которая будучи подставленной в уравнение, обращает его в тождество. Решение еще называется интегралом дифференциального уравнения.

Рассмотрим уравнение .

Функция является решением этого уравнения.

Действительно,

и уравнение обращается в тождество:
.
Решением рассматриваемого уравнения будут и функции

и вообще функции
, где и — произвольные постоянные.
В самом деле

и уравнение обращается в тождество
.

Заметим, что рассматриваемое уравнение имеет бесчисленное множество решений вида: .

Решение дифференциальных уравнений первого порядка

Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную x, искомую функцию y(x) и производную первого порядка искомой функции.

Дифференциальное уравнение первого порядка имеет вид .

Общее и частное решение

Общим решением дифференциального уравнения первого порядка называется решение , зависящее от одной произвольной постоянной C , придавая конкретное значение которой , можно получить решение , удовлетворяющее любому заданному начальному условию .

Равенство вида , неявно задающее общее решение, называется общим интегралом дифференциального уравнения.
Заметим, что в практике чаще всего бывает нужным не общее решение, а так называемое частное решение ,отвечающее определенным начальным условиям, вытекающим из условия данной конкретной задачи.
Частным решением называется любая функция , которая получается из общего решения ,если в последнем произвольной постоянной C придать определенное значение . Соотношение называется в этом случае частным интегралом .
Задача отыскания решения дифференциального уравнения y I = f(x,y) , удовлетворяющего заданным начальным условиям y(x o ) = y o , называется задачей Коши.

Теорема Коши
Если функция f(x,y) — правая часть дифференциального уравнения y I = f(x,y) — непрерывна в некоторой замкнутой области D плоскости xOy и имеет в этой области ограниченную частную производную f I y (x,y), то каждой внутренней точке области D соответствует, и притом единственное, решение, удовлетворяющее начальным условиям.

Рассмотрим уравнение
.

Общим решением этого уравнения является семейство функций
.

Действительно, при любом значении C эта функция удовлетворяет уравнению: .
Кроме того, всегда можно найти такое значение C, что соответствующее частное решение будет удовлетворять заданному начальному условию.

Найдем, например, частное решение, удовлетворяющее начальному условию y(1)=-2. Подставляя эти значения в уравнение
,
получим
.
Решая это уравнение относительно C получим C = — 3.
Следовательно, искомым частным решением будет функция: Y = X 2 — 3.

Это решение можно получить, используя нижеприведенный апплет для построения поля направлений и интегральных кривых для уравнения первого порядка.

С геометрической точки зрения общее решение уравнения первого порядка представляет собой семейство кривых на плоскости xOy , зависящее от одной произвольной постоянной C . Эти кривые называются интегральными кривыми данного дифференциального уравнения.
Частному решению соответствует одна интегральная кривая, проходящая через некоторую заданную точку. Так, в последнем примере общее решение геометрически изобразится семейством парабол, причем каждому значению параметра C будет соответствовать вполне определенная кривая. Частное решение изобразится параболой (рис. 1. ) проходящей через точку Заметим, что задать начальное условие для уравнения первого порядка с геометрической точки зрения означает задать точку , через которую должна пройти соответствующая интегральная кривая.

Решить или проинтегрировать данное дифференциальное уравнение это значит:

а) найти его общее решение или общий интеграл, если не заданы начальные условия,

б) найти частное решение, удовлетворяющее заданным начальным условиям.

Геометрическая интерпретация дифференциального уравнения первого порядка

Пусть дано дифференциальное уравнение, разрешенное относительно производной: .
Это уравнение для каждой точки определяет значение производной , т.е. определяет угловой коэффициент касательной к интегральной кривой, проходящей через эту точку.
Таким образом, рассматриваемое дифференциальное уравнение дает совокупность направлений или, как говорят, определяет поле направлений или поле линейных элементов . Задача интегрирования такого уравнения, с геометрической точки зрения, заключается в нахождении кривых, направление касательных к которым совпадает с направлением поля линейных элементов в соответствующих точках .

Рассмотрим уравнение
.
В каждой точке (x,y), отличной от точки (0,0), угловой коэффициент касательной к интегральной кривой равен отношению , т.е. совпадает с угловым коэффициентом прямой, проходящей через начало координат и точку с координатами (x,y). Очевидно, что интегральными кривыми будут прямые y=Cx, где C — произвольная постоянная, т.к. направление этих прямых всюду совпадает с направлением поля.

Теорема существования и единственности решения дифференциального уравнения.

Рассматривая уравнение первого порядка , разрешенное относительно производной, мы ставили вопрос об отыскании его общего решения и, если задано начальное условие частного решения, удовлетворяющего этому условию.
Возникает вопрос: всегда ли существует частное решение, удовлетворяющее заданному начальному условию и если существует, будет ли оно единственным.
Рассмотрим, например, уравнение
.
Общим решением является функция , а интегральными кривыми — семейство гипербол, причем через каждую точку , не лежащую на оси Oy проходит одна и только одна интегральная кривая, т.е. рассматриваемое уравнение имеет единственное решение, проходящее через точку, не лежащую на оси Oy , но оно не имеет решения, проходящего через точку, взятую на оси Oy .
Этот пример показывает, что не всегда существует решение, удовлетворяющее заданному начальному условию.
В некоторых случаях решение может оказаться не единственным.
Так, например, уравнение

имеет бесконечное множество решений, проходящих через точку (0,0) .
В самом деле, функция является общим решением этого уравнения, а при любом значении C прямая проходит через начало координат. На вопрос, при каких условиях для уравнения можно гарантировать существование и единственность решения, удовлетворяющего заданному начальному условию , отвечает следующая теорема.

Теорема.
Пусть функция и ее частная производная непрерывны в некоторой области D на плоскости xOy . Тогда, если точка принадлежит этой области, существует, и притом единственное, решение уравнения , удовлетворяющее начальному условию .

Геометрически это означает, что через каждую точку области D проходит одна и только одна интегральная кривая рассматриваемого уравнения. Данная теорема называется теоремой существования и единственности решения дифференциального уравнения .
Возвращаясь к рассмотренным нами примерам, мы видим, что функции

и

не определены при и, следовательно, не являются непрерывными. Это обстоятельство и привело, в первом случае, к отсутствию решений, проходящих через точки оси Ox , во втором — к нарушению единственности в точке (0,0) .

1.1. Уравнения с разделяющимися переменными

Рассмотрим уравнение первого порядка, разрешенное относительно производной:

или
.

Это уравнение можно переписать так:

или в симметричной форме

,

дающей соотношение между переменными x и y и их дифференциалами.

Если в этом уравнении функция P зависит только от x , а функция Q — только от y , то уравнение называется уравнением с разделенными переменными.

Таким образом, уравнением с разделенными переменными называется уравнение вида

.

Решение такого уравнения получается прямым интегрированием. Так как слева стоит сумма дифференциалов двух функций, которая равна нулю, то сумма их интегралов равняется постоянной

.

Уравнение — уравнение с разделенными переменными. Интегрируя, получим общий интеграл: .
Уравнение вида

называется уравнением с разделяющимися переменными .

Это уравнение может быть приведено к уравнению с разделенными переменными путем деления обеих его частей на выражение

или
.

Общий интеграл полученного уравнения имеет вид:

.

Дано уравнение
или .
Разделим переменные и интегрируем .

В результате вычисления получим:

.
Это выражение можно записать в иной форме:

т.к. всякое число можно представить в виде логарифма другого.

Таким образом, общий интеграл данного уравнения будет иметь вид

.

1.2. Однородные уравнения первого порядка

Рассмотрим сначала понятие однородной функции двух переменных.
Функция двух переменных называется однородной функцией измерения n , если при любом t справедливо тождество f (tx, ty) = t n f(x, y) .

Функция есть однородная функция измерения 2, т.к.
.

С понятием однородной функции связано понятие однородного дифференциального уравнения.

называется однородным дифференциальным уравнением первого порядка ,
если функции и являются однородными функциями одного и того же измерения.

Для однородного уравнения имеем:

.

Полагая в последних равенствах , получаем

.

Подставив эти выражения в исходное уравнение, получим

и далее .

Для разделения переменных введем новую переменную V = y/x или y = V x . Так как в этом случае dy = xd V + V dx , то последнее уравнение принимает вид:

M (1,V)dx + N(1,V)(xdV + Vdx) = 0 ,

[ M (1, V ) + vN (1, V )] dx + xN (1, V ) dV = 0 .

Последнее уравнение является уравнением с разделяющимися переменными x и V , из него определяется V , а затем искомая функция y = V x .

Если уравнение может приведено к виду: dy/dx = F(x,y) = F(v) , где V = y/x , то оно называется однородным дифференциальным уравнением первого порядка .

Для приведения его к уравнению с разделяющимися переменными используется подстановка
V = y/x , отсюда y = V x и dy/dx = xd V /dx + V .
В итоге получается уравнение с разделяющимися переменными: xd V /dx = F( V ) — V , которое и интегрируется.

Решить уравнение (y 2 — 3x 2 )dx + 2xydy = 0, при начальном условии: y(0) = 0 .

Здесь M(x,y) = (y 2 — 3x 2 ) и N(x,y) = 2xy — однородные функции измерения 2.

Применим подстановку y = vx, при этом dy = xdv +vdx.

Получим: x 2 (v 2 — 3)dx + 2x 2 v(xdv +vdx) = 0.
Сгруппируем слагаемые x 2 (v 2 — 3)dx + 2x 2 v(xdv +vdx) = 0 относительно dx и dv и разделим переменные:

.

После интегрирования получим: x 3 (v 2 — 1) = C или

общий интеграл: x(y 2 — x 2 ) = C

Используя начальные условия y(0) = 0 имеем 0(0 2 — 0 2 ) = C , отсюда C = 0.

Частное решение данного уравнения: x(y 2 — x 2 ) = 0

или x = y и x = — y

1.3. Линейные уравнения первого порядка

,

где и

— заданные непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

Если функция , стоящая в правой части уравнения, тождественно равна нулю, т.е. ,
то уравнение называется линейным однородным , в противном случае — линейным неоднородным .
Таким образом, — линейное однородное уравнение, а — линейное неоднородное уравнение.

Рассмотрим два метода интегрирования линейных уравнений.

I метод — метод Бернулли

Для решения уравнения применим подстановку y=UV , причем функцию U=U(x) будем считать новой неизвестной функцией, а функцию мы выберем произвольно, подчинив некоторому условию. Так как при этом , то эта подстановка дает:

и
.

Используя произвольный выбор функции V , подчиним ее условию: .

Разделяя переменные и интегрируя в последнем равенстве, получаем:

.
Поэтому исходное уравнение после подстановки полученной функции V(x) имеет вид: .
Это уравнение также является уравнением с разделяющимися переменными.
Решая его, получаем:
, а после интегрирования .

Возвращаясь к переменной y=UV имеем общее решение линейного неоднородного уравнения:
.

Решить уравнение .
Здесь .
Имеем:

— общее решение линейного уравнения.

II метод — метод вариации произвольной постоянной — метод Лагранжа

В линейном однородном уравнении переменные разделяются и его общее решение, которое мы обозначим через Y , легко находится:

.

Будем теперь находить общее решение неоднородного линейного уравнения , считая, что общее решение неоднородного уравнения y имеет такую же форму, как и общее решение cоответствующего однородного уравнения Y , но где C есть не постоянная величина, а неизвестная функция от x , т.е. считая, что

.

Дифференцируя это выражение

и подставляя в рассматриваемое неоднородное уравнение, получим:

или .
Откуда находим функцию C(x) :

.

.

Полученное общее решение состоит из двух слагаемых, из которых второе является общим решением соответствующего однородного уравнения, а первое является частным решением неоднородного уравнения, получаемым из общего при .

Найти общее решение уравнения
.

Интегрируем соответствующее однородное уравнение: .
Считаем C функцией x :
Подставляем в исходное уравнение:
.

1.4. Уравнение Бернулли

Уравнением Бернулли называется уравнение вида dy/dx + P(x)y = Q(x)y n .

При n = 0 или n = 1 уравнение становится линейным, методы интегрирования которого рассматривались в предыдущем пункте.

Есть следующие два способа интегрирования этого уравнения.

1 . Уравнение приводится к линейному.

Разделив все члены такого уравнения на y n , получим:

y -n (dy/dx) + P(x)y -n+1 = Q(x) .

Сделаем замену: y -n+1 = z . Тогда dz / dx = (- n +1) y — n dy / dx .

После подстановки этих выражений в уравнение оно примет вид:

dz/dx + (1-n)P(x)z = (1-n)Q(x) .

Это линейное уравнение относительно функции z . После его интегрирования возвращаемся к переменной y, подставив вместо z выражение y 1-n . Получим общий интеграл уравнения Бернулли.

2. Уравнение решается по методу Бернулли с подстановкой y = UV , уже использованному для решения линейных неоднородных уравнений.

Найти общее решение уравнения .

Разделив обе части уравнения на y 2 , получим:

.

Введем новую переменную , тогда .

Подставляя в уравнение, получим:

Это линейное уравнение относительно функции z( x ) .

Применим метод вариации произвольной постоянной:

Интегрируя по частям, находим ,

следовательно , .

Заменяя теперь z на ,
получим: или .
Это и есть общее решение исходного уравнения.

1.5. Уравнения в полных дифференциалах

Уравнением в полных дифференциалах называется уравнение вида

,

левая часть которого есть полный дифференциал некоторой функции , т.е.

.

Переписав исходное уравнение в виде , заключим, что общий интеграл этого уравнения определяется формулой .

Как известно, полный дифференциал функции выражается формулой

.

.

Необходимое и достаточное условие того, что левая часть уравнения является полным дифференциалом некоторой функции, выражается равенством

.

Функция , входящая в формулу , находится интегрированием функций P(x,y) и Q(x,y) соответственно по x и y при этом вторая переменная считается величиной постоянной (соответственно y или x ).

Проинтегрировать дифференциальное уравнение

.

Для данного уравнения

.

Так как выполнено условие (#), то данное уравнение является уравнением в полных дифференциалах, следовательно,

.

Интегрируя первое из этих уравнений ( y при этом считается постоянным), находим

,

где — функция подлежащая определению.

Дифференцируя по y функцию U(x,y) = C и принимая во внимание значение ,
получаем
,
откуда
.
Подставив выражение для

в равенство
,
найдем
.
В соответствии с формулой

получаем

или
,
где
.

Итак, общий интеграл данного уравнения:

Это уравнение является также однородным и его можно проинтегрировать другим способом.