Если система линейного уравнения равна 0

Если система линейного уравнения равна 0

СИСТЕМА ОДНОРОДНЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ

Системой однородных линейных уравнений называется система вида

Ясно, что в этой случае , т.к. все элементы одного из столбцов в этих определителях равны нулю.

Так как неизвестные находятся по формулам , то в случае, когда Δ ≠ 0, система имеет единственное нулевое решение x = y = z = 0. Однако, во многих задачах интересен вопрос о том, имеет ли однородная система решения отличные от нулевого.

Теорема. Для того, чтобы система линейных однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы Δ ≠ 0.

Итак, если определитель Δ ≠ 0, то система имеет единственное решение. Если же Δ ≠ 0, то система линейных однородных уравнений имеет бесконечное множество решений.

, а значит x=y=z=0.

СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ

Пусть задана квадратная матрица , X – некоторая матрица–столбец, высота которой совпадает с порядком матрицы A. .

Во многих задачах приходится рассматривать уравнение относительно X

,

где λ – некоторое число. Понятно, что при любом λ это уравнение имеет нулевое решение .

Число λ, при котором это уравнение имеет ненулевые решения, называется собственным значением матрицы A, а X при таком λ называется собственным вектором матрицы A.

Найдём собственный вектор матрицы A. Поскольку E∙X = X, то матричное уравнение можно переписать в виде или . В развёрнутом виде это уравнение можно переписать в виде системы линейных уравнений. Действительно .

И, следовательно,

Итак, получили систему однородных линейных уравнений для определения координат x₁, x₂, x₃ вектора X. Чтобы система имела ненулевые решения необходимо и достаточно, чтобы определитель системы был равен нулю, т.е.

Это уравнение 3-ей степени относительно λ. Оно называется характеристическим уравнением матрицы A и служит для определения собственных значений λ.

Каждому собственному значению λ соответствует собственный вектор X, координаты которого определяются из системы при соответствующем значении λ.

Найти собственные векторы и соответствующие им собственные значения матрицы .

Составим характеристическое уравнение и найдём собственные значения

При λ₁ = –1 получаем систему уравнений

Если x₁ = t, то, где t Î R.
Если λ₂ = 5

ВЕКТОРНАЯ АЛГЕБРА. ПОНЯТИЕ ВЕКТРОРА

При изучении различных разделов физики встречаются величины, которые полностью определяются заданием их численных значений, например, длина, площадь, масса, температура и т.д. Такие величины называются скалярными. Однако, кроме них встречаются и величины, для определения которых, кроме численного значения, необходимо знать также их направление в пространстве, например, сила, действующая на тело, скорость и ускорение тела при его движении в пространстве, напряжённость магнитного поля в данной точке пространства и т.д. Такие величины называются векторными.

Введём строгое определение.

Направленным отрезком назовём отрезок, относительно концов которого известно, какой из них первый, а какой второй.

Вектором называется направленный отрезок, имеющий определённую длину, т.е. это отрезок определённой длины, у которого одна из ограничивающих его точек принимается за начало, а вторая – за конец. Если A – начало вектора, B – его конец, то вектор обозначается символом, кроме того, вектор часто обозначается одной буквой . На рисунке вектор обозначается отрезком, а его направление стрелкой.

Модулем или длиной вектора называют длину определяющего его направленного отрезка. Обозначается || или ||.

К векторам будем относить и так называемый нулевой вектор, у которого начало и конец совпадают. Он обозначается . Нулевой вектор не имеет определенного направления и модуль его равен нулю ||=0.

Векторы и называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. При этом если векторы и одинаково направлены, будем писать , противоположно .

Векторы, расположенные на прямых, параллельных одной и той же плоскости, называются компланарными.

Два вектора и называются равными, если они коллинеарны, одинаково направлены и равны по длине. В этом случае пишут .

Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, помещая его начало в любую точку пространства.

1. Если дан вектор , то, выбрав любую точку , можем построить вектор , равный данному, и притом только один, или, как говорят, перенести вектор в точку .
   
2. Если рассмотреть квадрат ABCD, то на основанииопределения равенства векторов, мы можем написать и , но , , хотя все они имеют одинаковую длину.

ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ

Умножение вектора на число.

Произведением вектора на число λ называется новый вектор такой, что:

1. ;
2. вектор коллинеарен вектору ;
3. векторы и направлены одинаково, если λ>0 и противоположно, если λ

12. Однородная система линейных уравнений и ее решения

Система линейных уравнений

У которой столбец свободных членов — нулевой, называется однородной.

Однородная СЛУ (ОСЛУ) всегда совместна, так как нулевое решение (0,0,0) ей всегда удовлетворяет.

Поэтому, если однородная СЛУ имеет единственное решение, тогда оно — нулевое, так как для данного вида систем нулевое решение всегда имеет место.

Однородная СЛУ имеет ненулевые решения, если решений бесконечно много.

Утверждение 9. (Критерий существования ненулевых решений ОСЛУ).

Для того, чтобы однородная СЛУ имела ненулевые решения, необходимо и достаточно, чтобы определитель системы был равен нулю.

Пример №31. Решить однородную СЛУ

= = 30

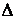
Определитель однородной системы отличен от нуля, следовательно решение единственное – нулевое.

Пример №32. Решить однородную СЛУ

= = 0

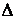
Определитель однородной системы равен нулю, следовательно — решений бесконечно много.

Общее решение ищем с помощью метода Гаусса

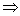
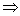
Далее записываем систему, соответствующую полученной ступенчатой матрице, и являющуюся эквивалентной исходной.

=> => ,

Решение систем линейных уравнений

Системы линейных уравнений имеют следующий общий вид:

$ \begin a_<1,1>\cdot x_ <1>+ a_<1,2>\cdot x_ <2>+ a_<1,3>\cdot x_ <3>+ \cdots a_ <1,n>\cdot x_ =b_ <1>\\ a_<2,1>\cdot x_ <1>+ a_<2,2>\cdot x_<2>+ a_<2,3>\cdot x_ <3>+ \cdots + a_<2,n>\cdot x_ = b_ <2>\\ a_<3,1>\cdot x_ <1>+ a_<3,2>\cdot x_<2>+a_<3,3>\cdot x_<3>+ \cdots + a_<3,n>\cdot x_=b_ <3>\\ \cdots\\ a_\cdot x_<1>+ a_\cdot x_<2>+a_\cdot x_<3>+\cdots + a_\cdot x_ =b_ \end$

$ A= \begin a_ <1,1>& a_ <1,2>& a_ <1,3>& . & . & a_ <1,n>\\ a_ <2,1>& a_ <2,2>& a_ <2,3>& . & . & a_ <2,n>\\ a_ <3,1>& a_ <3,2>& a_ <3,3>& . & . & a_ <3,n>\\ \cdots \\ a_ & a_ & a_ & . & . & a_ \end$ — матрица системы, а $b_<1>, b_<2>,b_ <3>\cdots b_$ — свободные члены системы.

Если все свободные члены равны 0, то система однородна.

Матрица системы — квадратная (m=n)

Надо вычислить определитель матрицы системы.

$\Delta = \begin a_ <1,1>& a_ <1,2>& a_ <1,3>& . & . & a_ <1,n>\\ a_ <2,1>& a_ <2,2>& a_ <2,3>& . & . & a_ <2,n>\\ a_ <3,1>& a_ <3,2>& a_ <3,3>& . & . & a_ <3,n>\\ \cdots \\ a_ & a_ & a_ & . & . & a_ \end$

Определитель матрицы системы не равен 0

Система называется невырожденной системой с единственным решением. Чтобы найти решение системы, используем метод Крамера.

Вычислим $ \Delta_>$ — определитель матрицы, полученной заменой столбца с коэффициентами соответствующей переменной $x_<1>$ столбцом свободных членов.
$\Delta_>= \begin b_ <1>& a_ <1,2>& a_ <1,3>& . & . & a_ <1,n>\\ b_ <2>& a_ <2,2>& a_ <2,3>& . & . & a_ <2,n>\\ b_ <3>& a_ <3,2>& a_ <3,3>& . & . & a_ <3,n>\\ \cdots \\ b_ & a_ & a_ & . & . & a_ \end$

Вычислим $ \Delta_>$ — определитель матрицы, полученной заменой столбца с коэффициентами соответствующей переменной $x_<2>$ столбцом свободных членов.
$\Delta_>= \begin a_ <1,1>& b_ <1>& a_ <1,3>& . & . & a_ <1,n>\\ a_ <2,1>& b_ <2>& a_ <2,3>& . & . & a_ <2,n>\\ a_ <3,1>& b_ <3>& a_ <3,3>& . & . & a_ <3,n>\\ \cdots \\ a_ & b_ & a_ & . & . & a_ \end$

Вычислим $ \Delta_>$ — определитель матрицы, полученной заменой столбца с коэффициентами соответствующей переменной $x_<3>$ столбцом свободных членов.
$\Delta_>= \begin a_ <1,1>& a_ <1,2>& b_ <1>& . & . & a_ <1,n>\\ a_ <2,1>& a_ <2,2>& b_ <2>& . & . & a_ <2,n>\\ a_ <3,1>& a_ <3,2>& b_ <3>& . & . & a_ <3,n>\\ \cdots \\ a_ & a_ & a_ & . & . & a_ \end$

Продолжаем делать это с остальными переменными, и в конце-концов записываем решение системы.
$x_=\dfrac<\Delta_>><\Delta>$

Пример 53
$\begin 2\cdot x + 3\cdot y -5\cdot z = \color<-7>\\ -3 \cdot x + 2\cdot y + z = \color<-9>\\ 4\cdot x — y + 2\cdot z = \color <17>\end$

Матрица системы:
$ \begin 2 & 3 & -5\\ -3 & 2 & 1\\ 4 & -1 & 2 \end$

Вычисляем определитель матрицы и получаем $\Delta = 8 -15 + 12 +40 +2 + 18 = 65$
Вычисляем $ \Delta_= \begin \color <-7>& 3 & -5\\ \color <-9>& 2 & 1\\ \color <17>& -1 & 2 \end= -28 — 45 + 51 + 170 — 7 +54 = 195$

Вычисляем $ \Delta_= \begin 2 & \color <-7>& -5\\ -3 & \color <-9>& 1\\ 4 & \color <17>& 2 \end=-36 + 255 -28 -180 -34 -42 = -65$

Вычисляем $ \Delta_= \begin 2 & 3 &\color<-7>\\ -3 & 2 & \color<-9>\\ 4 & -1 & \color <17>\end= 68 -21 -108 + 56 -18 + 153 =130$

Пример 54
$\begin 4\cdot x + 5\cdot y -2\cdot z = \color<3>\\ -2 \cdot x + 3\cdot y — z = \color<-3>\\ -1\cdot x — 2\cdot y + 3\cdot z = \color <-5>\end$

Матрица системы: $ \begin 4 & 5 & -2\\ -2 & 3 & -1\\ -1 & -2 & 3 \end$

Вычисляем определитель матрицы и получаем $\Delta = 36 -8 + 5 -6 -8 + 30 = 49$

Вычисляем $ \Delta_= \begin \color <3>& 5 & -2\\ \color <-3>& 3 &1\\ \color <-5>& -2 & 3 \end= 27 — 12 + 25 — 30 — 6 + 45 = 49$

Вычисляем $ \Delta_= \begin 4 & \color <3>& -2\\ -2 & \color <-3>& -1\\ -1 & \color <-5>& 3 \end=-36 -20+ 3 +6 -20 + 18 = -49$

Вычисляем $ \Delta_= \begin 4 & 5 & \color<3>\\ -2 & 3 & \color<-3>\\ -1& -2 & \color <-5>\end= -60 + 12 + 15 + 9 — 24 -50 = — 98$

Если система однородна, то ее решение есть <0;0;0>, потому что в матрицах, определителями которых являются $\Delta_$,$\Delta_$ и $\Delta_$, есть столбцы из одних нулей, следовательно, эти определители равны 0.

Пример 55
$\begin 2\cdot x + 3\cdot y -5\cdot z = \color<0>\\ -3 \cdot x + 2\cdot y + z = \color<0>\\ 4\cdot x — y + 2\cdot z = \color <0>\end$

Матрица системы:
$ \begin 2 & 3 & -5\\ -3 & 2 & 1\\ 4 & -1 & 2 \end$

Вычисляем определитель матрицы и получаем $\Delta = 8 -15 + 12 +40 +2 + 18 = 65 $

Определитель матрицы системы равен 0.

Вычисляем ранг матрицы системы и ранг расширенной матрицы (исходной матрицы, к которой добавлен столбец свободных членов).

Возможны следующие варианты:

• Если ранги этих матриц различны, то система не имеет решения. Это несовместная система.
• Если ранги равны, то система совместна и имеет бесконечное множество решений.

Решение системы находится следующим образом:

• Минор соответствующего ранга становится базисным минором.
• Переменные, коэффициенты при которых входят в базисный минор, становятся базисными (основными) переменными. Остальные переменные становятся свободными (неосновными), обозначаются другими буквами и переносятся в правую часть уравнений.
• Уравнения, содержащие базисный минор, становятся базисными уравнениями.
• Решаем систему, состоящую только из базисных уравнений, и находим решение системы, которое будет зависеть от неосновных переменных.
• Записываем решение.

Пример 56
$\begin 2\cdot x + 3\cdot y +2\cdot z = \color<5>\\ -3 \cdot x + 2\cdot y -3 \cdot z = \color<-1>\\ 4\cdot x — y + 4\cdot z = \color <3>\end$

Матрица системы:
$\begin 2 & 3 & 2\\ -3 & 2 & -3\\ 4 & -1 & 4 \end$

Вычисляем ранг матрицы:
$ 2\neq 0$

$\begin 2 & 3\\ -3 & 2 \end= 4 + 9 =13 \neq0$

$\begin 2 & 3 & 2\\ -3 & 2 & -3\\ 4 & -1 & 4 \end=0 $ (матрица имеет два равных столбца, следовательно, ее ранг равен 2)

Расширенная матрица:
$\begin 2 & 3 & 2 & \color<5>\\ -3 & 2 & -3 & \color<-1>\\ 4 & -1 & 4 & \color <3>\end$

Вычисляем ранг расширенной матрицы:
$ 2\neq 0$

$\begin 2 & 3\\ -3 & 2 \end= 4 + 9 =13 \neq0$

$\begin 2 & 3 & 2\\ -3 & 2 & -3\\ 4 & -1 & 4 \end=0$
$\begin 2 & 3 & \color<5>\\ -3 & 2 & \color<-1>\\ 4 & -1 & \color <3>\end=0 $ (матрица имеет два равных столбца, следовательно, ее ранг равен 2)

Поскольку ранги равны, система совместна и имеет бесконечное множество решений. Минор соответствующего ранга становится базисным минором.
$ \Delta_

= \begin 2 & 3\\ -3 & 2 \end$

Переменные x и y, коэффициенты при которых входят в базисный минор, становятся базисными переменными, а z становится неосновной переменной. Пусть $z=\alpha$. Первые два уравнения, в которых находится базисный минор, становятся базисными уравнениями. Решаем систему, состоящую из базисных уравнений.
$\begin 2\cdot x + 3\cdot y +2\cdot \alpha = 5\\ -3 \cdot x + 2\cdot y -3 \cdot\alpha = -1\\ \end=$ $\begin 2\cdot x + 3\cdot y = 5 — 2\cdot \alpha\\ -3 \cdot x + 2\cdot y = -1 + 3\cdot\alpha\\ \end$

Умножаем первое уравнение на 3, а второе на 2.
$\begin 6\cdot x + 9\cdot y = 15 — 6\cdot \alpha\\ -6 \cdot x + 4\cdot y = -2 + 6 \cdot \alpha \\ \end$

Складываем два полученные уравнения и получаем:
$ 13\cdot y = 13 \Rightarrow y = \dfrac<13> <13>= 1$

Умножаем первое уравнение на -2, а второе на 3.
$ \begin -4\cdot x — 6\cdot y = -10 + 4\cdot \alpha\\ -9 \cdot x + 6\cdot y = -3 + 9 \cdot \alpha \\ \end$

Складываем два полученные уравнения и получаем:
$ -13\cdot x = 13 \Rightarrow y = \dfrac<13\cdot\alpha -13> <13>= \alpha -1$
Решение системы: $\<\alpha-1;1;\alpha \>$

Пример 57
$\begin 2\cdot x + y +5\cdot z = \color<3>\\ 3 \cdot x + 2\cdot y +2 \cdot z = \color<1>\\ 7\cdot x +y + 12\cdot z = \color <2>\end$

Матрица системы:
$\begin 2 & 1 & 5\\ 3 & 2 & 2\\ 7 & 4 & 12 \end$

Вычисляем ранг матрицы:
$ 2\neq 0$
$\begin 2 & 1\\ 3 & 2 \end= 4 — 3 =1 \neq0$

$\begin 2 & 1 & 5\\ 3 & 2 & 2\\ 7 & 4 & 12 \end= 48 + 60 + 14 — 70 -16 -36 =0 $ (следовательно, ранг равен 2)

Расширенная матрица:
$\begin 2 & 1 & 5 & \color<3>\\ 3 & 2 & 2 & \color<1>\\ 7 & 4 & 12 & \color <2>\end$

Вычисляем ранг расширенной матрицы:
$ 2\neq 0$
$\begin 2 & 1\\ 3 & 2 \end= 4 -3 =1 \neq0$

$\begin 2 & 1 & 5\\ 3 & 2 & 2\\ 7 & 4 & 12 \end=0$

$\begin 2 & 1 & \color<3>\\ 3 & 2 & \color<1>\\ 7 & 4 & \color <2>\end= 8 + 36 + 7 — 42 -8 -6 = -5\neq 0 $

Ранг расширенной матрицы равен 3.

Поскольку ранги этих матриц различны, система не имеет решения. Это несовместная система. Однородная система всегда совместна и имеет бесконечное множество решений, поскольку ранг расширенной матрицы, содержащей столбец из одних нулей, всегда совпадает с рангом матрицы системы.

Пример 58
$\begin 2\cdot x + 3\cdot y +2\cdot z = \color<0>\\ -3 \cdot x + 2\cdot y -3 \cdot z = \color<0>\\ 4\cdot x — y + 4\cdot z = \color <0>\end$

Матрица системы:
$\begin 2 & 3 & 2\\ -3 & 2 & -3\\ 4 & -1 & 4 \end$

Вычисляем ранг матрицы:
$ 2\neq 0$
$\begin 2 & 3\\ -3 & 2 \end= 4 + 9 = 13 \neq0$

$ \begin 2 & 3 & 2\\ -3 & 2 & -3\\ 4 & -1 & 4 \end=0 $ (матрица имеет два равных столбца, следовательно, ее ранг равен 2)

Расширенная матрица:
$\begin 2 & 3 & 2 & \color<0>\\ -3 & 2 & -3 & \color<0>\\ 4 & -1 & 4 & \color <0>\end$

Вычисляем ранг расширенной матрицы:
$ 2\neq 0$
$\begin 2 & 3\\ -3 & 2 \end= 4 + 9 =13 \neq0$

$\begin 2 & 3 & 2\\ -3 & 2 & -3\\ 4 & -1 & 4 \end=0$

$ \begin 2 & 3 & \color<0>\\ -3 & 2 & \color<0>\\ 4 & -1 & \color <0>\end=0 $ (матрица включает столбец из одних нулей, следовательно, ее ранг равен 2)

Поскольку ранги равны, система совместна и имеет бесконечное множество решений. Минор соответствующего ранга становится базисным минором.
$\Delta_

= \begin 2 & 3\\ -3 & 2 \end$

Переменные x и y, коэффициенты при которых входят в базисный минор, становятся базисными переменными, а z становится неосновной переменной. Пусть $z=\alpha$. Первые два уравнения, в которых находится базисный минор, становятся базисными уравнениями. Решаем систему, состоящую из базисных уравнений.
$\begin 2\cdot x + 3\cdot y +2\cdot \alpha = 0\\ -3 \cdot x + 2\cdot y -3 \cdot\alpha = 0\\ \end=$ $\begin 2\cdot x + 3\cdot y = — 2\cdot \alpha\\ -3 \cdot x + 2\cdot y = 3\cdot\alpha\\ \end$

Умножаем первое уравнение на 3, а второе на 2.
$\begin 6\cdot x + 9\cdot y = -6\cdot \alpha\\ -6 \cdot x + 4\cdot y = 6 \cdot \alpha \\ \end$

Складываем два полученные уравнения и получаем:
$13\cdot y = 0 \Rightarrow y = \dfrac<0> <13>= 0$
Делаем то же самое, чтобы найти x. Умножаем первое уравнение на -2, а второе на 3.
$ \begin -4\cdot x — 6\cdot y = 4\cdot \alpha\\ -9 \cdot x + 6\cdot y =9 \cdot \alpha \\ \end$

Складываем два полученные уравнения и получаем:
$ -13\cdot x = 13 \Rightarrow y = \dfrac<13\cdot\alpha> <-13>= -\alpha$
Решение системы: $ \<-\alpha;0;\alpha \>$

Матрица системы не квадратная $(m\neq n)$

Вычисляем ранг матрицы системы и ранг расширенной матрицы (исходной матрицы, к которой добавлен столбец свободных членов).

Возможны следующие варианты:

• Если ранг этих матриц различен, то система не имеет решения. Это несовместная система.
• Если ранги равны, то система совместна и имеет бесконечное множество решений.
  Решение системы находится следующим образом:
  • Минор соответствующего ранга становится базисным минором.
  • Переменные, коэффициенты при которых входят в базисный минор, становятся базисными (основными) переменными. Остальные переменные становятся свободными (неосновными), обозначаются другими буквами и переносятся в правую часть уравнений.
  • Уравнения, содержащие базисный минор, становятся базисными уравнениями.
  • Решаем систему, состоящую только из базисных уравнений, и находим решение системы, которое будет зависеть от неосновных переменных.
  • Записываем решение.

Пример 59
$\begin 2\cdot x + 3\cdot y +2\cdot z = \color<5>\\ -3 \cdot x + 2\cdot y -3 \cdot z = \color<-1>\\ \end$

Матрица системы:
$\begin 2 & 3 & 2\\ -3 & 2 & -3\\ \end$

Вычисляем ранг матрицы:
$ 2\neq 0$
$\begin 2 & 3\\ -3 & 2 \end= 4 + 9 =13 \neq0$ (ранг равен 2)

Расширенная матрица:
$\begin 2 & 3 & 2 & \color<5>\\ -3 & 2 & -3 & \color<-1>\\ \end$

Вычисляем ранг расширенной матрицы:
$ 2\neq 0$
$\begin 2 & 3\\ -3 & 2 \end= 4 + 9 =13 \neq0$ (ранг также равен 2)

Поскольку ранги равны, система совместна и имеет бесконечное множество решений. Минор соответствующего ранга становится базисным минором.

Переменные x и y, коэффициенты при которых входят в базисный минор, становятся базисными переменными, а z становится неосновной переменной. Пусть $z=\alpha$. Первые два уравнения, в которых находится базисный минор, становятся базисными уравнениями. Решаем систему, состоящую из базисных уравнений.

$\begin 2\cdot x + 3\cdot y +2\cdot \alpha = 5\\ -3 \cdot x + 2\cdot y -3 \cdot\alpha = -1\\ \end=$ $\begin 2\cdot x + 3\cdot y = 5 — 2\cdot \alpha\\ -3 \cdot x + 2\cdot y = -1 + 3\cdot\alpha\\ \end$

Умножаем первое уравнение на 3, а второе на 2.
$\begin 6\cdot x + 9\cdot y = 15 — 6\cdot \alpha\\ -6 \cdot x + 4\cdot y = -2 + 6 \cdot \alpha \\ \end$

Складываем два полученные уравнения и получаем:
$ 13\cdot y = 13 \Rightarrow y = \dfrac<13> <13>= 1$
Делаем то же самое, чтобы найти x. Умножаем первое уравнение на -2, а второе на 3.
$ \begin -4\cdot x — 6\cdot y = -10 + 4\cdot \alpha\\ -9 \cdot x + 6\cdot y = -3 + 9 \cdot \alpha \\ \end$

Складываем два полученные уравнения и получаем:
$-13\cdot x = 13 \Rightarrow y = \dfrac<13\cdot\alpha -13> <13>= \alpha -1$
Решение системы: $\<\alpha-1;1;\alpha \>$

Пример 60
$\begin 2\cdot x + 3\cdot y = \color<5>\\ -3 \cdot x + 2\cdot y = \color<-1>\\ 4\cdot x — y = \color <3>\end$

Матрица системы:
$\begin 2 & 3 \\ -3 & 2 \\ 4 & -1 \end$

Вычисляем ранг матрицы:
$2\neq 0$
$\begin 2 & 3\\ -3 & 2 \end= 4 + 9 =13 \neq0$ (ранг равен 2)

Расширенная матрица:
$\begin 2 & 3 & \color<5>\\ -3 & 2 & \color<-1>\\ 4 & -1 & \color <3>\end$

Вычисляем ранг расширенной матрицы:
$2\neq 0$
$\begin 2 & 3\\ -3 & 2 \end= 4 + 9 =13 \neq0$
$\begin 2 & 3 & \color<5>\\ -3 & 2 & \color<-1>\\ 4 & -1 & \color <3>\end=0 $ (матрица имеет два равных столбца, следовательно, ее ранг равен 2)

Поскольку ранги равны, система совместна и имеет бесконечное множество решений. Минор соответствующего ранга становится базисным минором.
$\Delta_

= \begin 2 & 3\\ -3 & 2 \end$

Переменные x и y, коэффициенты при которых входят в базисный минор, становятся базисными переменными, а z становится неосновной переменной. Система не имеет неосновных переменных. Первые два уравнения, в которых находится базисный минор, становятся базисными уравнениями. Решаем систему, состоящую из базисных уравнений.
$\begin 2\cdot x + 3\cdot y = 5\\ -3 \cdot x + 2\cdot y = -1\\ \end$

Умножаем первое уравнение на 3, а второе на 2.
$\begin 6\cdot x + 9\cdot y = 15\\ -6 \cdot x + 4\cdot y = -2 \\ \end$

Складываем два полученные уравнения и получаем:
$13\cdot y = 13 \Rightarrow y = \dfrac<13> <13>= 1$
Делаем то же самое, чтобы найти x. Умножаем первое уравнение на -2, а второе на 3.
$ \begin -4\cdot x — 6\cdot y = -10\\ -9 \cdot x + 6\cdot y = -3\\ \end$

Складываем два полученные уравнения и получаем:
$ -13\cdot x = -13 \Rightarrow y = \dfrac<-13> <-13>= 1$
Убедимся, что результаты удовлетворяют неосновному уравнению.
$4\cdot1 -1\cdot1 = 3$
Решение системы: $\<1;1 \>$