Если уравнение тела дано как

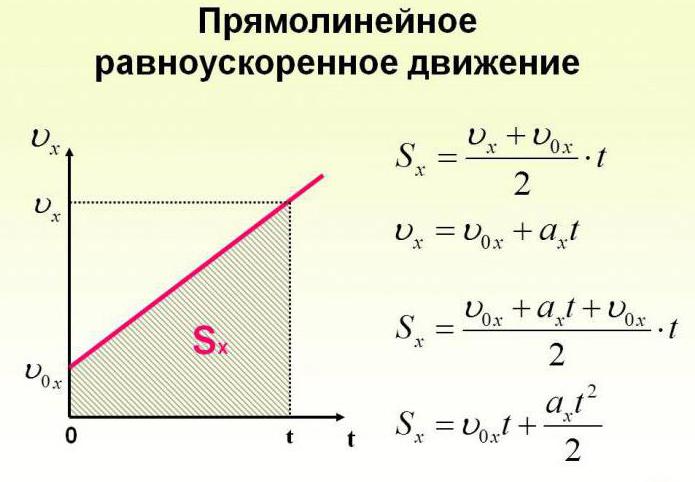
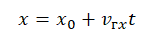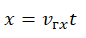Уравнение движения тела. Все виды уравнений движения

Понятие «движение» определить не так уж просто, как это может показаться. С житейской точки зрения, это состояние является полной противоположностью покоя, но современная физика считает, что это не совсем так. В философии под движением подразумеваются любые изменения, происходящие с материей. Аристотель полагал, что данное явление равносильно самой жизни. А для математика любое перемещение тела выражается уравнением движения, записанным при помощи переменных и цифр.

Материальная точка

В физике перемещение различных тел в пространстве изучает раздел механики, именуемый кинематикой. Если размеры некоего объекта слишком малы в сравнении с расстоянием, которое ему приходится преодолевать вследствие его движения, то он рассматривается здесь как материальная точка. Примером тому может служить автомобиль, едущий по дороге из одного города в другой, птица, летящая в небе, а также многое другое. Подобная упрощенная модель удобна при написании уравнения движения точки, за которую принимается определённое тело.

Бывают и другие ситуации. Представим, что тот же автомобиль хозяин решил переместить с одного конца гаража в другой. Здесь изменение местоположения сравнимо с размерами объекта. Поэтому каждая из точек автомобиля будет иметь разные координаты, а сам он рассматривается как объёмное тело в пространстве.

Основные понятия

Следует учитывать, что для физика путь, пройденный определённым объектом, и перемещение – совсем не одно и то же, а эти слова не являются синонимами. Уяснить разницу между данными понятиями можно, рассмотрев движение самолёта в небе.

След, который он оставляет, наглядно показывает его траекторию, то есть линию. При этом путь представляет собой её длину и выражается в определённых единицах (к примеру, в метрах). А перемещение – это вектор, соединяющий лишь точки начала и конца движения.

Подобное можно увидеть на рисунке, приведённом ниже, который демонстрирует маршрут машины, едущей по извилистой дороге, и вертолёта, летящего по прямой. Векторы перемещения для этих объектов будут одинаковые, а пути и траектории – разными.

Равномерное движение по прямой

Теперь рассмотрим различные виды уравнений движения. И начнём с самого простого случая, когда некий объект перемещается по прямой с одинаковой скоростью. Это значит, что по истечении равных промежутков времени путь, который он проходит за данный период, не меняется по величине.

Что нам потребуется для описания данного движения тела, вернее, материальной точки, как уже было условлено его называть? Важно выбрать систему координат. Для простоты предположим, что перемещение происходит вдоль некоей оси 0Х.

Тогда уравнение движения: x = х₀ + v_хt. Оно и будет описывать процесс в общем виде.

Важным понятием при изменении местоположения тела является скорость. В физике она является векторной величиной, поэтому принимает положительное и отрицательное значение. Здесь всё зависит от направления, ведь тело может перемещаться по выбранной оси с возрастающей координатой и в противоположную сторону.

Относительность движения

Почему так важно выбрать систему координат, а также точку отсчёта для описания указанного процесса? Просто потому, что законы мироздания таковы, что без всего этого уравнение движения не будет иметь смысла. Это показано такими великими учёными, как Галилей, Ньютон и Эйнштейн. С начала жизни, находясь на Земле и интуитивно привыкнув выбирать её за систему отсчёта, человек ошибочно полагает, что существует покой, хотя для природы не бывает такого состояния. Тело может менять местоположение или оставаться статичным лишь относительно какого-либо объекта.

Мало того, тело может двигаться и находиться в покое одновременно. Примером тому может послужить чемодан пассажира поезда, который лежит на верхней полке купе. Он движется относительно деревни, мимо которой проезжает состав, и покоится по мнению своего хозяина, расположившегося на нижнем сидении у окна. Космическое тело, некогда получив начальную скорость, способно лететь в пространстве миллионы лет, пока не столкнётся с другим объектом. Движение его не будет прекращаться потому, что перемещается оно лишь относительно прочих тел, а в системе отсчёта, связанной с ним, космический путешественник находится в покое.

Пример составления уравнений

Итак, выберем за точку отсчёта некий пункт А, при этом координатной осью пусть будет для нас автомагистраль, находящаяся рядом. А направление её будет проходить с запада на восток. Предположим, что в эту же сторону в пункт В, расположенный за 300 км, пешком отправился путешественник со скоростью 4 км/ч.

Получается, что уравнение движения задаётся в виде: х = 4t, где t – время в пути. Согласно этой формуле, появляется возможность вычислить местонахождение пешехода в любой необходимый момент. Становится понятно, что через час он пройдёт 4 км, через два – 8 и достигнет пункта Б спустя 75 часов, так как его координата х = 300 окажется при t = 75.

Если скорость отрицательна

Предположим теперь, что из В в А едет автомобиль, имея скорость 80 км/час. Здесь уравнение движения имеет вид: х = 300 – 80t. Это действительно так, ведь х₀ = 300, а v = -80. Следует обратить внимание, что скорость в данном случае указывается со знаком «минус», потому что объект перемещается в отрицательном направлении оси 0Х. Через какое время автомобиль достигнет пункта назначения? Это произойдёт, когда координата примет нулевое значение, то есть при х = 0.

Остаётся решить уравнение 0 = 300 – 80t. Получаем, что t = 3,75. Это означает, что автомобиль достигнет пункта В через 3 часа 45 минут.

Необходимо помнить, что координата тоже может быть отрицательной. В нашем случае это оказалось бы, если б существовал некий пункт С, находящийся в западном направлении от А.

Движение с увеличением скорости

Перемещаться объект может не только с постоянной скоростью, но и менять её с течением времени. Движение тела может происходить по очень сложным законам. Но для простоты следует рассмотреть случай, когда ускорение увеличивается на определённое постоянное значение, а объект перемещается по прямой. В данном случае говорят, что это равноускоренное движение. Формулы, описывающие этот процесс, приведены ниже.

А теперь рассмотрим конкретные задачи. Допустим, что девочка, сев на санки на вершине горы, которую мы выберем за начало воображаемой системы координат с направлением оси по наклону вниз, начинает двигаться под действием силы тяжести с ускорением, равным 0,1 м/с 2 .

Тогда уравнение движения тела имеет вид: s_x = 0,05t 2 .

Понимая это, можно узнать расстояние, которое девочка проедет на санках, для любого из моментов перемещения. Через 10 секунд это будет 5 м, а через 20 секунд после начала движения под гору путь составит 20 м.

Как выразить скорость на языке формул? Поскольку v_0x = 0 (ведь санки начали катиться с горы без начальной скорости только под действием силы притяжения), то запись не будет слишком сложной.

Уравнение скорости движения примет вид: v_x= 0,1t. Из него мы сможет узнать, как изменяется этот параметр с течением времени.

К примеру, через десять секунд v_x= 1 м/с 2 , а через 20 с примет значение 2 м/с 2 .

Если ускорение отрицательно

Существует и другой вид перемещения, относящийся к тому же типу. Это движение называют равнозамедленным. В данном случае скорость тела тоже изменяется, но с течение времени не увеличивается, а уменьшается, и тоже на постоянную величину. Снова приведём конкретный пример. Поезд, ехавший до этого с постоянной скоростью 20 м/с, начал тормозить. При этом ускорение его составило 0,4 м/с 2 . Для решения примем за начало отсчёта точку пути поезда, где он начал тормозить, а координатную ось направим по линии его перемещения.

Тогда становится понятно, что движение задано уравнением: s_x = 20t — 0,2t 2 .

А скорость описывается выражением: v_x = 20 – 0,4t. Необходимо заметить, что перед ускорением ставится знак «минус», так как поезд тормозит, и данная величина отрицательна. Из полученных уравнений возможно заключить, что состав остановится через 50 секунд, проехав при этом 500 м.

Сложное движение

Для решения задач в физике обычно создаются упрощённые математические модели реальных ситуаций. Но многогранный мир и явления, происходящие в нём, далеко не всегда вписываются в подобные рамки. Как составить уравнение движения в сложных случаях? Проблема решаема, ведь любой запутанный процесс возможно описать поэтапно. Для пояснения снова приведём пример. Вообразим, что при запуске фейерверков одна из ракет, взлетевшая с земли с начальной скоростью 30 м/с, достигнув верхней точки своего полёта, разорвалась на две части. При этом соотношение масс получившихся осколков составило 2:1. Далее обе части ракеты продолжили двигаться отдельно одна от другой таким образом, что первая полетела вертикально вверх со скоростью 20 м/с, а вторая сразу упала вниз. Следует узнать: какова была скорость второй части в момент, когда она достигла земли?

Первым этапом данного процесса окажется полёт ракеты вертикально вверх с начальной скоростью. Перемещение будет равнозамедленным. При описании понятно, что уравнение движения тела имеет вид: s_x = 30t – 5t 2 . Здесь мы полагаем, что ускорение свободного падения для удобства округляется до значения 10 м/с 2 . Скорость при этом будет описываться следующим выражением: v = 30 – 10t. По этим данным уже возможно вычислить, что высота подъёма составит 45 м.

Вторым этапом движения (в данном случае уже второго осколка) окажется свободное падение этого тела с начальной скоростью, получаемой в момент распадения ракеты на части. При этом процесс будет равноускоренным. Для нахождения окончательного ответа сначала вычисляет v₀ из закона сохранения импульса. Массы тел относятся 2:1, а скорости находятся в обратной зависимости. Следовательно, второй осколок полетит вниз с v₀ = 10 м/c, а уравнение скорости примет вид: v = 10 + 10t.

Время падения мы узнаем из уравнения движения s_x = 10t + 5t 2 . Подставим уже полученное значение высоты подъёма. В результате выходит, что скорость второго осколка приблизительно равна 31,6 м/с 2 .

Таким образом, разделяя сложное движение на простые составные части, можно решать любые запутанные задачи и составлять уравнения движения всех видов.

Уравнение координаты при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Уравнение координаты — зависимость координаты тела от времени:

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x₀ = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с 2 . Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v₀ = 0 м/с.

В момент времени t = 10 c координата автомобиля равна:

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

1. Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
2. Построить уравнение вида x₁ = x₂.
3. Найти время встречи двух тел t_встр.
4. Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату x_встрч.

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

x = 3t = 3∙6 = 18 (м).

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

1. Построить графики x1(t) и x2(t).
2. Найти точку пересечения графиков.
3. Пустить перпендикуляр из этой точки к оси ОХ.
4. Значение точки пересечения — координата места пересечения двух тел.

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с 2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с 2 , достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

Алгоритм решения

1. Определить характер движения материальной точки.
2. Записать уравнение координаты материальной точки.
3. С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.

Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет вид: 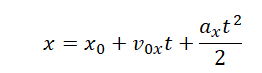Ветви параболы смотрят вверх. Это значит, что коэффициент перед квадратом переменной величины (времени) стоит положительный коэффициент. Следовательно, a_x>0. Поэтому варианты «б» и «г» исключаются. Остается выяснить, чему равна скорость: она равна нулю (как в ответе «а») или меньше нуля (как в ответе «в»)? Моменту времени t=0 соответствует точка, являющая вершиной параболы. Когда ветви параболы смотрят вверх, в ее вершине скорость тела всегда равна нулю, так как эта точка лежит на границе между отрицательной и положительной скоростью. Отсюда делаем вывод, что верный ответ «а».Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

1. Записать исходные данные.
2. Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
3. Выразить скорость грузовика из уравнения его движения.
4. Записать уравнение движения мотоциклиста.
5. Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
6. Подставить время в формулу скорости грузовика и вычислить ее.

Решение

• Координата встречи грузовика и мотоциклиста: x = 150 м.
• Время запаздывания мотоциклиста: t_запазд = 5 с.
• Ускорение, с которым мотоциклист начал движение: a = 3 м/с 2 .

Запишем уравнение движения грузовика:

Так как начальная координата равна нулю, это уравнение примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Отсюда скорость движения грузовика равна:

Запишем уравнение движения мотоциклиста:

Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:

Найдем время, через которое грузовик и мотоциклист встретились:

Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Физика

План урока:

Механическое движение. Система отсчёта. Закон относительности движения

Механическим движением в физике называется изменение с течением времени положения тела (или его частей) в пространстве относительно других тел.

То есть, чтобы сказать, что тело или система совершает механическое движение, нам необходимо: 1) наблюдать его во времени; 2) сравнивать его положение с положением какого-то другого тела (относительно этого тела).

Например, пассажир в едущем автомобиле неподвижен относительно кресла, на котором он сидит, но он движется относительно людей, стоящих на автобусной остановке и самой остановки. А сама автобусная остановка неподвижна относительно стоящих людей, ждущих автобус (см. рисунок 1). Однако она движется относительно проезжающих мимо машин. В первом случае наблюдаемым объектом был человек в машине, а точкой отсчета кресло и люди на остановке. Во втором случае наблюдаемой была автобусная остановка, а точками отсчета – люди на остановке и проезжающие мимо машины.

Рисунок 1 – Иллюстрация к примеру

Из примеров можно сделать вывод, что важно, какой именно объект находится под наблюдением и относительно какого объекта – тела отсчета – рассматривается его движение. Отсюда можно сформулировать закон относительности движения: характер движения тела зависит от того, относительно какого объекта мы рассматриваем данное движение.

Тело (или точка) отсчета, связанная с ним система координат и часы, вместе образуют систему отсчета. То есть все сказанное выше можно переформулировать в одно предложение: для наблюдения механического движения важно в какой системе отсчета будет происходить наблюдение.

Рисунок 2 – Пример системы отсчета (наблюдаемы объект – летящий мяч, тело отсчета – камень, лежащий в начале координат, система координат и секундомер для отсчета времени)

Однако объекты могут быть очень сложными для наблюдения. Например, автомобиль едет по прямой несколько километров и необходимо описать его движение относительно камня на обочине. Казалось бы, все просто. Но как именно описать движение автомобиля, если корпус его движется по прямой, а колеса совершают вращательные движения.

Для удобства решения подобных задач принято упрощение: если размер и форма тела в данной задаче не играют важной роли для наблюдателя, можно считать это тело за материальную точку.

Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь.

Приведем пример: когда автобус едет из города А в город Б, его можно рассматривать как материальную точку. Когда пассажир идет из одного конца этого автобуса в другой, считать автобус материальной точкой нельзя. В общем случае можно сказать, что тело можно считать материальной точкой, если его размеры значительно меньше расстояния, на которое оно перемещается.

Уравнения движения. Радиус-вектор. Проекция вектора

Для описания движения тела необходимо уметь рассчитывать его положение в каждый момент времени. Как это сделать?

Самый очевидный способ – координатный. Если вернуться к примеру на рисунке 2, можно увидеть, что летящий мяч в каждый момент времени имеет три координаты по осям OX, OY и OZ. Эти координаты являются функциями времени (т.е. они зависят от времени), а значит, их можно записать в виде системы:

Вид этих уравнений будет зависеть от многих вещей: от того, с какой силой бросили мяч в начале, от массы мяча, под каким углом его бросили и так далее. В любом случае, если эти уравнения заданы, можно найти координаты (то есть положение) тела в любой момент времени. Поиск этих уравнений – основная задача кинематики.

Эта система является кинематическими уравнениями движения тела или материальной точки, записанными в координатной форме. Повторим: если вид уравнений движения задан, можно узнать координату движущейся точки в любой момент времени.

В общем случае, координат три, но иногда можно обойтись двумя или даже одной координатой. Например, для описания движения бильярдного шара достаточно двух координат (так как шар не может двигаться вверх и вниз), а для описания движения шарика, катящегося по прямому горизонтальному желобку достаточно одной координаты (шарик не может двигаться вверх-вниз и вправо-влево).

Еще один способ описания движения – векторный.

*Перед дальнейшим прочтением данной статьи желательно вспомнить основную теорию по теме «Векторы» и «Метод координат»

Вектор, проведенный из начала координат к материальной точке, называется радиус-вектором (см. рисунок 3).

Рисунок 3 – Радиус-вектор (серой линией изображены траектория движения материальной точки, r₁ и r₂* радиус-векторы, проведенные к этой материальной точке в разные моменты времени)

Радиус-вектор проведенный к материальной точке в разные моменты времени будет разным. Значит, его тоже можно представить, как функцию времени:

r = r(t)

Такая функция и будет уравнением движения в векторной форме. Если ее вид задан, можно описать движение тела с той же полнотой, как и при координатной записи.

Еще раз обозначим отличия: при записи уравнения движения в координатной форме в каждый момент времени наблюдающий будет знать три координаты тела; при записи в векторной форме в каждый момент времени известен радиус-вектор (его модуль и направление). Обе записи равносильны.

*На письме векторы обычно обозначаются стрелкой сверху, над величиной. Однако в печатном тексте не всегда удобно нагромождать формулы дополнительными знаками, поэтому в печати векторные величины пишут просто жирным шрифтом. В данной статье далее жирным шрифтом будут написаны только векторные величины.

Покажем, что векторная и координатная записи равносильны. Для этого необходимо вспомнить, как построить проекцию вектора на ось (см. рисунок 4).

Рисунок 4 – Построение проекции вектора на ось

Чтобы построить проекцию вектора на ось, необходимо опустить перпендикуляра из начала и конца вектора на эту ось. Длина получившегося отрезка между проекциями начала и конца вектора, взятая со знаком «+», если вектор а сонаправлен с осью Х, или со знаком «-», если вектор а противонаправлен оси Х, — это и есть искомая проекция.

Если вектор выходит из начала координат, задача облегчается – необходимо опустить перпендикуляр только из конца вектора.

Напоминания из геометрии:

два вектора равны, если они параллельны или лежат на одной прямой, сонаправлены, а их модули равны;

проекции равных векторов равны.

Рассмотрим пример (см. рисунок 5)

Рисунок 5 – Задача на нахождение проекции векторов

Предлагаем читателю самому подумать, а затем сравнить свои рассуждения с приведенными ниже.

Итак, вектор а: его начала соответствует координате х_н=1, а конец х_к = 4. Значит a_x = х_к – х_н = 4-1 = 3. Вектор b: его начало лежит в точке х_н=2, а конец х_к =0. Значит b_x = х_к – х_н = 0-2 = -2.

В двумерном случае, проецировать нужно на две оси, но принцип остается тем же.

Иногда еще нужно находить составляющие компоненты вектора а_х и а_у. Рассмотрим пример, для простоты возьмем вектор, выходящий из начал координат (см. рисунок 6).

Сумма векторов а_х и а_у равна а. Модули векторов а_х и а_у численно равны координатам точек, куда попали перпендикуляры, опущенные из конца вектора а на оси ОХ и ОУ.

Еще следует отметить, что, если известен угол β между вектором а и осью ОХ, воспользовавшись основами тригонометрии, можно найти величины проекций:

Если бы вектор а совпадал с радиус-вектором какой-нибудь точки, то величины а_х и а_у совпадали бы с координатами тела по осям ОХ и ОY.

Способ с использованием тригонометрических функций удобен, когда координата конца вектора попадает в нецелое число и опустив перпендикуляр на ось его трудно найти точно. В физических задачах такое часто случается.

Рисунок 6 – Нахождение компонент вектора а

Рассмотрим пример (см. рисунок 7). Модуль вектора r равен 2. Сам вектор направлен под углом в 45 градусов к оси ОХ. Необходимо найти величины проекций (они же координаты) этого вектора на оси ОХ и ОУ.

Рисунок 7 – Задача на нахождение проекций вектора в двумерном пространстве

В общем случае радиус-вектор находится в трехмерном пространстве (см. рисунок 8). Построение проекции осуществляется по тому же принципу, что и в рассмотренных выше примерах. Когда строятся проекции на оси ОХ и ОУ, перпендикуляр сначала опускается на плоскость, в которой лежат оси ОХ и ОУ, а затем точка, в которую упал перпендикуляр к плоскости, проецируется на оси ОХ и ОУ.

Точки, в которые попал перпендикуляры к осям – r_x, r_y, r_z – это и есть координаты x, y, z тела в текущий момент времени.

Следует оговориться, что большинство задач 10-го класса будут ограничиваться двумерным пространством.

Рисунок 8 – Построение проекций радиус-вектора

Траектория. Путь. Перемещение

Траектория – это линия, вдоль которой движется тело.

Траектория движения может быть прямолинейной, если тело движется по прямой линии, и криволинейной, если тело движется по кривой.

Путь (S), пройденный телом, равен длине траектории.

Перемещение (r)* – это вектор, проведенный из начала пути в конец.

В случае прямолинейного движения путь и модуль перемещения тела совпадают (см. рисунок 9а). В случае криволинейного – путь и перемещение различаются (см. рисунок 9б), так как длина линии движения тела больше длины вектора, соединяющего начало и конец траектории.

Рисунок 9 – Путь (S) и перемещение (r) при прямолинейном (а) и криволинейном (б) движении

*Иногда перемещение так же, как и путь, называют буквой S — (на письме с вектором над ней, при печати — жирным шрифтом, так как это векторная величина). В данной статье, чтобы не путаться, перемещение называется только буквой r. В целом, обозначения равноправны, поэтому при решении задач можно использовать то, которое удобнее. Однако не стоит забывать отмечать, что именно обозначено под той или иной буквой.

Равномерное прямолинейное движение: скорость и уравнение движения

Путь и перемещение при равномерном прямолинейном движении

Прямолинейное равномерное движение уже рассматривалось в курсе физики ранее, однако приведем основные определения.

Прямолинейное движение – это движение по прямой линии. Равномерное движение – такое, в процессе которого тело за равные временные промежутки проходит один и тот же путь. Если объединить эти два определения получится третье:

• равномерное прямолинейное движение – это такое движение, в ходе которого 1) тело совершает движение по прямой линии; 2) за одинаковые временные промежутки проходит одинаковый путь.

Зная определения пути и перемещения, это определение можно упростить: прямолинейное равномерное движение тела – это такое движение, в процессе которого тело за одинаковые временные промежутки совершает равные перемещения.

Важной характеристикой является скорость механического движения. Предположим, что при равномерном прямолинейном движении тело за промежуток времени △t перемещается из точки А в точку Б (см. рисунок 8). Радиус-вектор, проведенный в точку A обозначим r₀, а радиус-вектор в точку Б обозначим r₁. Изменение радиус-вектора назовем △r – нетрудно заметить, что это есть перемещение тела за время △t.

Рисунок 8 – Поиск перемещения тела через радиус-векторы при равномерном прямолинейном движении

Тогда скорость движения (v) будет вычисляться по формуле:

Так как △r – вектор, △t – скаляр, скорость v тоже будет вектором, сонаправленным перемещению.

Если тело начинает двигаться в момент начала отсчета, то △t = t*. Из правила сложения векторов следует, что △r = r₁ — r₀. Тогда выражение для скорости можно переписать в виде:

Из этого выражения следует:

Это выражение можно применить к любому произвольно взятому моменту времени, поэтому можно опустить индекс в левой части и переписать:

Данное уравнение является уравнением движения при прямолинейном равномерном движении.

*Напоминание: символом △ (дельта) обозначают изменение какой-нибудь величины. Например △t = t – t₁, где t – конечный момент времени, t₁ – начальный. Если же начальный момент времени совпадает с началом отсчета t₁ = 0, то △t = t – 0 = t_.

Фактически уравнение равномерного прямолинейного движения означает, что радиус-вектор в произвольный момент времени t можно посчитать, сложив начальный радиус-вектор и приращение v*t.

Найдя проекции радиус-вектора и вектора скорости, можно разложить уравнение движения тела на три составляющие вдоль осей ОX, ОY и ОZ.

В этих выражениях r_0x, r_0y, r_0z и v_x, v_y, v_z – это компоненты изначальных векторов r₀ и v вдоль осей ОХ, ОY и ОZ соответственно. И теперь можно перейти к скалярному виду:

Стоит отметить, что при проецировании какие-то компоненты вектора могут стать отрицательными, тогда знаки в выражениях поменяются на противоположные.

В рассмотренном выше примере движение происходит только вдоль оси ОХ (остальные координаты не изменяются). На рисунке 9 приведены проекции начальной (х₀) и конечной (х₁) точки на ось ОХ.

Рисунок 9 – Перемещение тела в координатном представлении

Уравнение координаты (х) движения будет выглядеть:

А это уже похоже на знакомую из прошедшего курса физики формулу для нахождения пути:

Если точка начала двигаться из начала отсчета S₀ = 0, можно переписать эту формулу в виде:

Отсюда следуют известные уже формулы для нахождения скорости и времени при равномерном прямолинейном движении:

Приведем последний в этой статье пример: известно, что тело движется вдоль оси ОХ, начиная из точки x₀ = 3 см. Скорость тела равна v = 5 м/с и направлена вдоль оси ОХ. Необходимо записать уравнение движения по координате х для этого тела.

Итак, для начала приведем все единицы измерения к СИ:

Теперь можно записывать уравнение для координаты х:

Из этого уравнения можно найти координату тела в любой момент времени. Например, через 2 секунды после начала отсчета тело находилось в точке:

x(2) = 0,03 + 5*2 = 10, 03.

А какой путь прошло тело к этому моменту? В начале оно находилось в точке x(2) = 0,03 м, а через 2 секунды оно стало находиться в точке x(2) = 10, 03. Значит за 2 секунды тело прошло:

S = x(2) – x₀ = 10, 03 – 0,03 = 10 м.

А если скорость тела была направлена противоположно оси ОХ, как тогда выглядело бы уравнение движения?

Тогда проекция вектора скорости на ось ОХ была бы отрицательной и в уравнении знак перед скоростью поменялся бы на противоположный: