Решения задач линейного программирования
Задачу линейного программирования (ЛП) можно решать аналитическими и графическими методами. Аналитические методы являются основой для решения задачи на ЭВМ. Их единственный недостаток состоит в том, что в отличие от графических методов, они недостаточно наглядны. Графические методы очень наглядны, но они пригодны лишь для решения задач на плоскости, т.е. когда размерность пространства К=2. Однако, учитывая большую наглядность графических методов, с их помощью рассмотрим идею решения задачи ЛП на примере задачи распределения ресурсов.
Однако прежде чем заняться решением, сделаем некоторые замечания. Пусть мы имеем систему m уравнения с n неизвестными (I).
Возможны следующие варианты:
À Число неизвестных меньше, чем число уравнений n m. Например:
Очевидно, что это уравнение прямой, и все значения x1 и x2, лежащие на этой прямой, являются решением уравнения (4.2). Значит уравнение (4.5) имеет бесчисленное множество решений.
В случае, когда система имеет больше одного возможного решения, может быть поставлена задача оптимизации, суть которой в том, что из всех допустимых решений, удовлетворяющих ограничениям и граничным условиям, выбрать такое, которое придает целевой функции оптимум. Вспомним построение линейных зависимостей. Пусть дано уравнение:
Преобразуем его к виду:
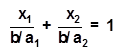
Запись (4.7) называют уравнением прямой в отрезках, что изображено на Рис. 4.1. Рассмотрим еще одну форму представления уравнения (4.6). Запишем это уравнение в виде:
Уравнение (4.8) изображено на рис. 4.2.
 |
 |
Вспомним неравенства. Если линейное уравнение с двумя переменными может быть представлено в виде прямой на плоскости, то неравенство вида:
изображается как полуплоскость, показанная на рис. 4.1. На этом рисунке часть плоскости, удовлетворяющая неравенству, заштрихована. Координаты всех точек, принадлежащих заштрихованному участку, имеют такие значения x1 и x2, которые удовлетворяют заданному неравенству. Значит, эти значения составляют область допустимых решений (ОДР). Саму прямую считаем принадлежащей каждой из двух указанных полуплоскостей. Предположим теперь, что задано не одно неравенство, а система:
где первое неравенство определяет некоторую полуплоскость П1, второе — полуплоскость П2 и т.д.
если какая-либо пара чисел (x1, x2) удовлетворяет всем неравенствам (4.10), то, соответствующая точка Р(x1, x2), принадлежит всем полуплоскостям П1, П2, . Пm одновременно. Другими словами, точка Р принадлежит пересечению (общей части) полуплоскостей П1, П2, . Пm, т.е. некоторой многоугольной области М (Рис. 4.3), которая является ОДР. Вдоль контура области изображены штрихи, идущие внутрь области. Они одновременно указывают, с какой стороны от данной прямой лежит соответствующая полуплоскость, то же самое указано и с помощью стрелок на каждой линии. Сразу же отметим, что ОДР не всегда бывает, ограничена: в результате пересечения нескольких полуплоскостей может возникнуть и неограниченная область (Рис. 4.4). Возможен и случай, когда область допустимых решений (ОДР) пуста. Это означает, что система (5.7) противоречива (Рис. 4.5). Многоугольник ОДР обладает весьма важным свойством: он является выпуклым.
 |
 |
 |
þ фигура называется выпуклой, если вместе с любыми двумя своими точками А и В, она содержит и весь отрезок АВ.
В случае трех неизвестных, каждое уравнение представляет собой плоскость в пространстве. Каждая плоскость разбивает все пространство на два полупространства. Система неравенств определяет в пространстве выпуклый объемный многогранник, который представляет ОДР.
Условие совместности системы линейных уравнений. Теорема Кронекера-Капелли
Установить, совместна ли система линейных уравнений, с помощью теоремы Кронекера-Капелли часто можно быстрее, чем с помощью метода Гаусса, когда требуется последовательно исключать неизвестные. Основана эта теорема на использовании ранга матрицы.
Теорема Кронекера-Капелли о совместности системы. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы этой системы равен рангу её расширенной матрицы, то есть чтобы 
Здесь матрица A (матрица системы) — это матрица, составленная из коэффициентов при неизвестных:
В свою очередь матрица В (расширенная матрица) — это матрица, полученная присоединением к матрице системы столбца из свободных членов:
Ранги этих матриц связаны неравенством 
Следствие из теоремы Кронекера-Капелли о числе решений. Пусть для системы m линейных уравнений с n неизвестными выполнено условие совместности, то есть ранг матрицы из коэффициентов системы равен рангу её расширенной матрицы. Тогда верно следующее.
- Если ранг матрицы равен числу неизвестных (
), то система имеет единственное решение.
- Если ранг матрицы системы меньше числа неизвестных (
), то система имеет бесконечно много решений, а именно: некоторым n — r неизвестным можно придавать произвольные значения, тогда оставшиеся r неизвестных определятся уже единственным образом.
Если ранг матрицы системы линейных уравнений равен числу уравнений, то есть 
В ходе доказательства теоремы Кронекера-Капелли были получены явные формулы для решений системы (в случае её совместности). Если уже известно, что система совместна, то, чтобы найти её решения, необходимо:
1) отыскать в матрице системы A ранга 

2) отбросить те уравнения, которые соответствуют строкам матрицы A, не входящим в минор 
3) члены с коэффициентами, не входящими в 

Пример 1. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений
Если система совместна, то решить её.
Решение. Вычисляем ранг матрицы этой системы и ранг расширенной матрицы. В обоих случаях он равен 3. Следовательно, система линейных уравнений совместна. Так как ранг матрицы системы меньше числа неизвестных, то система имеет бесконечно много решений: одно неизвестное может быть взято произвольно. Минор
отличен от нуля, поэтому последнее уравнение отбрасываем и неизвестному 

Оставшиеся неизвестные определяются из системы
Решая последнюю систему по формулам Крамера или иным способом, находим



Присоединяя сюда 
Пример 2. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений
Если система совместна, то решить её.
Решение. Вычисляем ранг матрицы этой системы:

Следовательно, ранг системы равен 3. Определим ранг расширенной матрицы:

Это означает, что ранг расширенной матрицы также равен 3. Следовательно, система совместна, а так как число неизвестных равно рангу матрицы системы, то она имеет единственное решение. Для решения можем использовать первые три уравнения:
Решая последнюю систему по формулам Крамера, находим



53. Однородные системы уравнений
Линейное уравнение называется Однородным, если его свободный член равен нулю, и неоднородным в противном случае. Система, состоящая из однородных уравнений, называется однородной и имеет общий вид:
Очевидно, что всякая однородная система совместна и имеет нулевое (тривиальное) решение. Поэтому применительно к однородным системам линейных уравнений часто приходится искать ответ на вопрос о существовании ненулевых решений. Ответ на этот вопрос можно сформулировать в виде следующей теоремы.
Теорема. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных.
Доказательство: Допустим, система, ранг которой равен, имеет ненулевое решение. Очевидно, что 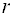
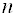
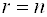
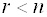
Следствие 1: Однородная система уравнений, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.
Доказательство: Если у системы уравнений 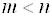
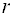
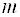
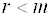
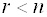
Следствие 2: Однородная система 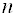
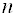
Доказательство: Допустим, система 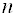
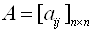
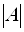
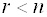
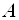
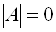
http://function-x.ru/systems_kroneker_kapelli.html
http://matica.org.ua/metodichki-i-knigi-po-matematike/analiticheskaia-geometriia-lineinaia-algebra/53-odnorodnye-sistemy-uravnenii



 ), то система имеет единственное решение.
), то система имеет единственное решение. ), то система имеет бесконечно много решений, а именно: некоторым n — r неизвестным можно придавать произвольные значения, тогда оставшиеся r неизвестных определятся уже единственным образом.
), то система имеет бесконечно много решений, а именно: некоторым n — r неизвестным можно придавать произвольные значения, тогда оставшиеся r неизвестных определятся уже единственным образом.




