Этап отделения корней нелинейного уравнения

3.1. Отделение корней нелинейного уравнения

Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a, b], которому он принадлежит.

На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней.

В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается Аналитическими и Графическими методами.

Аналитические методы основаны на функциональном анализе.

Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида

Pn(x) = an x n + an-1xn-1 +. +a1x+ a0 = 0, (an >0) (3.2)

Верхняя граница положительных действительных корней определяется по формуле Лагранжа (Маклорена):

, (3.3)

Где: k ³ 1 – номер первого из отрицательных коэффициентов полинома;

B – максимальный по модулю отрицательный коэффициент.

Нижнюю границу положительных действительных корней можно определить из вспомогательного уравнения

(3.4)

Если для этого уравнения по формуле Лагранжа верхняя граница равна R1, то

= (3.5)

Тогда все положительные корни многочлена лежат в интервале

≤x+≤.

Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.

и .

≤x–≤ = =.

Рассмотрим пример отделения корней с использованием этого аналитического метода.

Методом Лагранжа определим границы положительных и отрицательных корней многочлена.

3×8 – 5×7 – 6×3 – x – 9 = 0

K = 1 B = |– 9| an = 3

= 4

9×8 + x7 + 6×5 + 5x – 3 = 0

k = 8 B = 3 an = 9

Отсюда границы положительных корней 0,5 ≤ x+ ≤ 4

3×8 + 5×7 + 6×3 + x – 9 = 0

=

9×8 – x7 – 6×5 – 5x – 3 = 0

K = 1 B = 6 an = 9

Следовательно, границы отрицательных корней –2 ≤ x– ≤ –0,6

Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования.

Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других.

На практике получил большее распространение Графический метод приближённой оценки вещественных корней. Для этих целей строится график функции по вычисленным её значениям.

Графически корни можно отделить 2-мя способами:

1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.На графике 3 корня.

Рис. 3.1 Отделение корней на графике f(x).

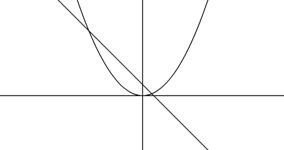
2. Преобразовать f(x)=0 к виду j(x) = y(x), где j(x) и y(x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.

На графике 2 корня.

Рис. 3.2 Отделение корней по графикам функций j(x) и y(x).

Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.

Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте Изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный.

Рассмотрим Схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции.

Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня.

Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня.

Недостаток метода – использование большого количества машинного времени.

3.1. Отделение корней нелинейного уравнения.

Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a,b], которому он принадлежит.

На первом этапе определяется число корней, их тип.

В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается аналитическими и графическими методами.

Аналитические методы основаны на функциональном анализе.

Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида

Pn(x) = an x n + an-1xn-1 +. +a1x+ a0 = 0, (an >0) (3.2)

верхняя граница положительных действительных корней определяется по формуле Лагранжа (Маклорена):

, (3.3)

где: k ? 1 – номер первого из отрицательных коэффициентов полинома;

B – максимальный по модулю отрицательный коэффициент.

Нижнюю границу положительных действительных корней можно определить из вспомогательного уравнения

(3.4)

Если для этого уравнения по формуле Лагранжа верхняя граница равна R1, то

= (3.5)

Тогда все положительные корни многочлена лежат в интервале

≤x+≤.

Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.

и .

≤x–≤ = =.

Рассмотрим пример отделения корней с использованием этого аналитического метода.

Методом Лагранжа определим границы положительных и отрицательных корней многочлена.

3×8 – 5×7 – 6×3 – x – 9 = 0

k = 1 B = |– 9| an = 3

= 4

9×8 + x7 + 6×5 + 5x – 3 = 0

k = 8 B = 3 an = 9

Отсюда границы положительных корней 0,5 ≤ x+ ≤ 4

3×8 + 5×7 + 6×3 + x – 9 = 0

=

9×8 – x7 – 6×5 – 5x – 3 = 0

k = 1 B = 6 an = 9

Следовательно, границы отрицательных корней –2 ≤ x– ≤ –0,6

Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования.

Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других.

На практике получил большее распространение графический метод приближённой оценки вещественных корней. Для этих целей строится график функции по вычисленным её значениям.

Графически корни можно отделить 2-мя способами:

1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.

На графике 3 корня.

x* Î [a,b]

Рис. 3.1 Отделение корней на графике f(x).

2. Преобразовать f(x)=0 к виду j(x) = y(x), где j(x) и y(x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.

На графике 2 корня.

x1* Î [a,b]

Рис. 3.2 Отделение корней по графикам функций j(x) и y(x).

Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.

Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный.

Рассмотрим схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции.

Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня.

Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня.

Недостаток метода – использование большого количества машинного времени.

Электронная библиотека

Приближенное решение уравнения состоит из двух этапов:

1) отделения корней, то есть нахождения интервалов из области определения функции f(x), в каждом из которых содержится только один корень уравнения (3.1).

2) уточнения корней до заданной точности.

Отделение корней можно проводить графически и аналитически. Для того чтобы графически отделить корни уравнения (3.1), необходимо построить график функции y = f(x). Абсциссы точек его пересечения с осью Ox являются действительными корнями уравнения (рис. 3.1).

На практике же бывает удобнее заменить уравнение (3.1) равносильным ему уравнением:

где , – более простые функции, чем f(x).

Абсциссы точек пересечения графиков функций и дают корни уравнения (3.2), а значит и исходного уравнения (3.1) (рис. 3.2).

Аналитическое отделение корней основано на следующих теоремах:

Теорема 1. Если непрерывная функция y = f(x) принимает на концах отрезка значения разных знаков, т.е. , то на этом отрезке содержится, по крайней мере, один корень уравнения (3.1) (рис. 3.3).

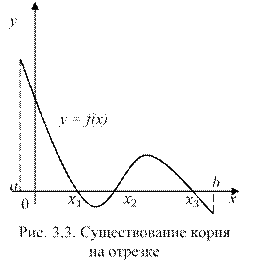
Теорема 2. Если непрерывная на отрезке функция y = f(x) принимает на концах отрезка значения разных знаков, а производная сохраняет знак внутри отрезка , то внутри отрезка существует единственный корень уравнения (рис. 3.4):

Уточнение корней до заданной точности заключается в сужении интервала изоляции корня и выполняется одним из специальных методов. Наиболее распространенными являются методы: деления отрезка пополам; касательных (Ньютона); секущих (хорд).

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00