Этапы численного решения нелинейного уравнения

Численное решение нелинейного уравнения. Этапы решения.

f(x)=0, где f(x) – произвольная функция, наиболее распространенная в инж. Практике задача по отысканию корней.

Выбор метода решения зависит от вида f(x). Для численного решения нелинейных уравнений применяются только итерационные методы.

Задача нахождения корней состоит из 2 этапов:

1. Отделение корней – определение числа корней и их примерного расположения на числовой оси.

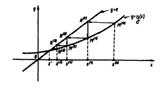
Наиболее применим графический способ отделения корней, т. е. отыскание точек пересечения ф. f(x) с осью абсцисс:

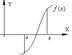
[a;b] – интервал изоляции корня. Для каждого корня уравнения определяется интервал его изоляции [a;b]. На отрезке [a;b] должен находиться 1 корень.

2. Уточнение корней – вычисление каждого корня с заданной степенью точности.

Классификация методов уточнения корней :

1) Метод половинного деления отрезка(дихотомии).

Отрезок [a;b], содержащий единственный корень, делят пополам, отбрасывают ту половину, где нет корня. Процесс повторяется до тех пор, пока длина отрезка не станет меньше заданной погр. E.

Достоинства: прост и надежен, всегда сводится к решению независимо от вида ф. f(x). Недостаток: самый медленный из всех известных методов уточн. Корня.

Построение последовательных хорд, в качестве приближений к корню принимаются значения их пересечения с осью абсцисс.

Достоинство: простота. Недостаток: быстрота сходимости к решению сильно зависит от вида ф. f(x).

3) Метод касательных( метод Ньютона)

В качестве приближения к корню ищется точка пересечения касательной с осью абсцисс.

Достоинство: высокая скорость. Недостатки: ограничения на вид ф. (должна быть дифференцируема, f’(x) и f’’(x) не должны менять знак на интервале уточнения корня).

4) Комбинированный метод – объединение методов хорд и касательных.

Приближение к корню на каждой итерации происходит одновременно с 2 сторон интервала [a;b]. Одной стороны строится хорда, а с другой касательная.

Достоинство: работает быстрее, чем методы хорд и касательных. Недостатки: f(x) должна быть дифференцируема; f’(x) иf’’(x) не должны менять знак на интервале уточнения корня; трудности с дифф-ем f(x).

5) Метод простой итерации.

Исходное нелинейное уравнения заменяется равносильным уравнением x=g(x)и с помощью сходящегося итерационного процесса происходит приближение к корню, пока не достигнет предела заданной погрешности Е.

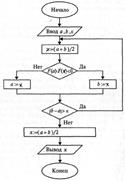
45)Уточнение корня нелинейного уравнения методом половинного деления(дихотомии). Алгоритм. Требуется вычислить корень уравнения f(x)=0 на [a;b] с заданной погрешностью Е. Отрезок [a;b], содержащий единственный корень, делят на 2 половины, отбрасывают ту из них, где нет корня. Процесс продолжается до тех пор, пока длина отрезка не станет меньше заданной погрешности Е.

Алгоритм метода:

46)Уточнение корня нелинейного уравнения методом хорд. Схема алгоритма.Требуется вычислить корень уравнения f(x)=0 на [a,b] с заданной погрешностью е. Геометр-ки метод основан на построении последовательности хорд. Ур-е хорды . В данном методе процесс итерации состоит в том, что в качестве приближений к корню уравнение f(x)=0 принимаются значения х₁, х₂… х_i точек пересечения хорды АВ с осью абсцисс. Если f(a)>0 , то левая граница a неподвижна, х₀=b и из урав. хорды получим: Если f(a) 0 и f’’(x)>0 при a≤x≤b. Тогда для приближения к корню со стороны границы а используем построение хорды, а со стороны границы b – касательная. На 1й итерации строим хорду А₀В₀ и проводим касательную в точку В₀. Левую границу а переносим в а₁, правую – b_1. На каждой итерации для вычисления новых границ интервала используют ф-лы хорд и касательных : , . Сужение интервала проводим до тех пор пока он не станет

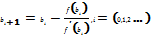
Численные методы решения систем нелинейных уравнений

Введение

Многие прикладные задачи приводят к необходимости нахождения общего решения системы нелинейных уравнений. Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.

Следует отметить интересный факт о том, что любая система уравнений над действительными числами может быть представлена одним равносильным уравнением, если взять все уравнения в форме , возвести их в квадрат и сложить.

Для численного решения применяются итерационные методы последовательных приближений (простой итерации) и метод Ньютона в различных модификациях. Итерационные процессы естественным образом обобщаются на случай системы нелинейных уравнений вида:

(1)

Обозначим через вектор неизвестных и определим вектор-функцию Тогда система (1) записывается в виде уравнения:

(2)

Теперь вернёмся к всеми любимому Python и отметим его первенство среди языков программирования, которые хотят изучать [1].

Этот факт является дополнительным стимулом рассмотрения числительных методов именно на Python. Однако, среди любителей Python бытует мнение, что специальные библиотечные функции, такие как scipy.optimize.root, spsolve_trianular, newton_krylov, являются самым лучшим выбором для решения задач численными методами.

С этим трудно не согласится хотя бы потому, что в том числе и разнообразие модулей подняло Python на вершину популярности. Однако, существуют случаи, когда даже при поверхностном рассмотрении использование прямых известных методов без применения специальных функций библиотеки SciPy тоже дают неплохие результаты. Иными словами, новое- это хорошо забытое старое.

Так, в публикации [2], на основании проведенных вычислительных экспериментов, доказано, что библиотечная функция newton_krylov, предназначенная для решения больших систем нелинейных уравнений, имеет в два раза меньшее быстродействие, чем алгоритм TSLS+WD
(two-step least squares), реализованный средствами библиотеки NumPy.

Целью настоящей публикации является сравнение по числу итераций, быстродействию, а главное, по результату решения модельной задачи в виде системы из ста нелинейных алгебраических уравнений при помощи библиотечной функции scipy.optimize.root и методом Ньютона, реализованного средствами библиотеки NumPy.

Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений

Библиотечная функция scipy.optimize.root выбрана в качестве базы сравнения, потому что имеет обширную библиотеку методов, пригодных для сравнительного анализа.

scipy.optimize.root(fun, x0, args=(), method=’hybr’, jac=None, tol=None,callback=None, ptions=None)
fun — Векторная функция для поиска корня.
x0 –Начальные условия поиска корней

method:
hybr -используется модификация Пауэлл гибридный метод;
lm – решает системы нелинейных уравнений методом наименьших квадратов.
Как следует из документации [3] методы broyden1, broyden2, anderson, linearmixing, diagbroyden, excitingmixing, krylov являются точными методами Ньютона. Остальные параметры являются «не обязательными» и с ними можно ознакомится в документации.

Методы решения систем нелинейных уравнений

Приведенный далее материал действительно можно прочитать в литературе, например в [4], но я уважаю своего читателя и для его удобства приведу вывод метода по возможности в сокращенном виде. Те, кто не любит формулы, этот раздел пропускают.

В методе Ньютона новое приближение для решения системы уравнений (2) определяется из решения системы линейных уравнений:

(3)

Определим матрицу Якоби:

(4)

Запишем(3) в виде:

(5)

Многие одношаговые методы для приближенного решения (2) по аналогии с двухслойными итерационными методами для решения систем линейных алгебраических уравнений можно записать в виде:

(6)

где — итерационные параметры, a — квадратная матрица n х n, имеющая обратную.

При использовании записи (6) метод Ньютона (5) соответствует выбору:

Система линейных уравнений (5) для нахождения нового приближения может решаться итерационно. В этом случае мы имеем двухступенчатый итерационный процесс с внешними и внутренними итерациями. Например, внешний итерационный процесс может осуществляться по методу Ньютона, а внутренние итерации — на основе итерационного метода Зейделя

При решении систем нелинейных уравнений можно использовать прямые аналоги стандартных итерационных методов, которые применяются для решения систем линейных уравнений. Нелинейный метод Зейделя применительно к решению (2) дает:

(7)

В этом случае каждую компоненту нового приближения из решения нелинейного уравнения, можно получить на основе метода простой итерации и метода Ньютона в различных модификациях. Тем самым снова приходим к двухступенчатому итерационному методу, в котором внешние итерации проводятся в соответствии с методом Зейделя, а внутренние — с методом Ньютона.

Основные вычислительные сложности применения метода Ньютона для приближенного решения систем нелинейных уравнений связаны с необходимостью решения линейной системы уравнений с матрицей Якоби на каждой итерации, причем от итерации к итерации эта матрица меняется. В модифицированном методе Ньютона матрица Якоби обращается только один раз:

(8)

Выбор модельной функции

Такой выбор не является простой задачей, поскольку при увеличении числа уравнений в системе в соответствии с ростом числа переменных результат решения не должен меняться, поскольку в противном случае невозможно отследить правильность решения системы уравнений при сравнении двух методов. Привожу следующее решение для модельной функции:

Функция f создаёт систему из n нелинейных уравнений, решение которой не зависит от числа уравнений и для каждой из n переменных равно единице.

Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней

Только один из методов, приведенных в документации [3] прошёл тестирование по результату решения модельной функции, это метод ‘krylov’.

Решение для n=100:

Вывод: С увеличением числа уравнений вдвое заметно появление ошибок в решении. При дальнейшем увеличении n решение становится не приемлемым, что возможно из-за автоматической адаптации к шагу, эта же причина резкого падения быстродействия. Но это только моё предположение.

Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона

Решение для n=100:

Решение для n=200:

Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1.]
Newton iteration = 14
Newton method time 1.869 seconds

Чтобы убедиться в том, что программа действительно решает систему, перепишем модельную функцию для ухода от корня со значением 1 в виде:

Получим:
Solution:
[ 0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
Newton iteration = 16
Newton method time 0.046 seconds

Вывод: Программа работает и при изменении модельной функции.

Теперь вернёмся к начальной модельной функции и проверим более широкий диапазон для n, например в 2 и 500.
n=2
Solution:
[1. 1.]
Newton iteration = 6
Newton method time 0.048 seconds
n=500

Численные методы решения нелинейных уравнений

Если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы (т.е. имеют одну независимую переменную), то такая модель, как правило, описывается одним нелинейным уравнением.

Необходимость отыскания корней нелинейных уравнений встречается в расчетах систем автоматического управления и регулирования, собственных колебаний машин и конструкций, в задачах кинематического анализа и синтеза, плоских и пространственных механизмов и других задачах.

Дано нелинейное уравнение:

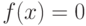( 4.1)

Необходимо решить это уравнение, т. е. найти его корень .

Если функция имеет вид многочлена степени m,

где a_i — коэффициенты многочлена, 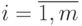, то уравнение f(x)=0 имеет m корней (рис. 4.2).

Если функция f(x) включает в себя тригонометрические или экспоненциальные функции от некоторого аргумента x , то уравнение (4.1) называется трансцендентным уравнением .

Такие уравнения обычно имеют бесконечное множество решений.

Как известно, не всякое уравнение может быть решено точно. В первую очередь это относится к большинству трансцендентных уравнений .

Доказано также, что нельзя построить формулу, по которой можно было бы решать произвольные алгебраические уравнения степени, выше четвертой.

Однако точное решение уравнения не всегда является необходимым. Задачу отыскания корней уравнения можно считать практически решенной, если мы сумеем найти корни уравнения с заданной степенью точности . Для этого используются приближенные (численные) методы решения.

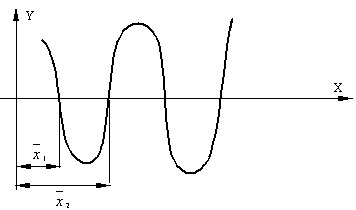
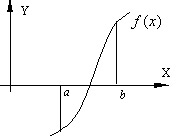
Большинство употребляющихся приближенных методов решения уравнений являются, по существу, способами уточнения корней. Для их применения необходимо знание интервала изоляции [a,b] , в котором лежит уточняемый корень уравнения (рис. 4.3).

Процесс определения интервала изоляции [a,b] , содержащего только один из корней уравнения, называется отделением этого корня.

Процесс отделения корней проводят исходя из физического смысла прикладной задачи, графически, с помощью таблиц значений функции f(x) или при помощи специальной программы отделения корней. Процедура отделения корней основана на известном свойстве непрерывных функций: если функция непрерывна на замкнутом интервале [a,b] и на его концах имеет различные знаки, т.е. f(a)f(b) , то между точками a и b имеется хотя бы один корень уравнения (1). Если при этом знак функции f'(x) на отрезке [a,b] не меняется, то корень является единственным на этом отрезке.

Процесс определения корней алгебраических и трансцендентных уравнений состоит из 2 этапов:

отделение корней, — т.е. определение интервалов изоляции [a,b] , внутри которого лежит каждый корень уравнения;
уточнение корней, — т.е. сужение интервала [a,b] до величины равной заданной степени точности .

Для алгебраических и трансцендентных уравнений пригодны одни и те же методы уточнения приближенных значений действительных корней:

источники:

http://habr.com/ru/post/419453/

http://intuit.ru/studies/courses/2260/156/lecture/27239
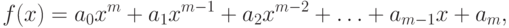
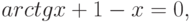