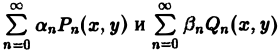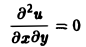Уравнения с частными производными, Эванс Л.К., 2003
Уравнения с частными производными, Эванс Л.К., 2003.
Фундаментальный труд выдающегося американского математика Л. К. Эванса является вводным курсом в теорию дифференциальных уравнений с частными производными. Учебник состоит из трех частей. Часть I содержит материал, традиционно включаемый в основные курсы дифференциальных уравнений: уравнение Лапласа, уравнение переноса, волновое уравнение и уравнение теплопроводности. Рассматриваются классические свойства решений, а также функции Грина, фундаментальные решения, энергетические методы, методы Фурье, Лапласа, Лежандра, метод годографа, асимптотические методы и метод разложения в степенные ряды. В ч. II, посвященной теории линейных уравнений, вводится понятие слабого решения, изложены теория пространств Соболева, общие теоремы существования и регулярности слабых решений для эллиптических, параболических, гиперболических уравнений второго порядка, а также для гиперболических систем первого порядка. Третья часть знакомит с современными методами исследования нелинейных уравнений. Наряду с вариационным методом широко представлены невариационные подходы, основанные на различных идеях: монотонность, теоремы о неподвижных точках, супер- и субрешения, субдифференциалы и нелинейные полугруппы. Представлены теория уравнений Гамильтона — Якоби и некоторые элементы теории оптимального управления. Подробно изучены системы законов сохранения, задача Римана (о распаде разрыва), ударные волны и энтропийный критерий. В приложении даны необходимые сведения из математического анализа, теории меры и функционального анализа. Книга доступна студентам, изучающим математику и физику. Представляет интерес для преподавателей ВУЗов и научных сотрудников.
ПРИМЕРЫ.
Не существует общей теории, устанавливающей разрешимость всех уравнений с частными производными. Весьма сомнительно, что создание такой теории вообще возможно ввиду большого многообразия физических, геометрических и вероятностных явлений, которые моделируются уравнениями с частными производными. Поэтому исследования концентрируются вокруг некоторых конкретных уравнений, важных для приложений, как в рамках самой математики, так и для смежных дисциплин, с надеждой, что интуитивное понимание истоков этих уравнений с частными производными подскажет путь к их решению.
Содержание.
Глава 1.Введение.
Часть I.ФОРМУЛЫ ПРЕДСТАВЛЕНИЯ РЕШЕНИЙ.
Глава 2.Четыре важных линейных уравнения с частными производными.
Глава 3.Нелинейные уравнения с частными производными первого порядка.
Глава 4.Другие методы представления решений.
Часть II.ТЕОРИЯ ЛИНЕЙНЫХ УРАВНЕНИЙ.
Глава 5.Пространства Соболева.
Глава 6.Эллиптические уравнения второго порядка.
Глава 7.Линейные эволюционные уравнения.
Часть III.ТЕОРИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
Глава 8.Вариационное исчисление.
Глава 9.Невариационные методы.
Глава 10.Уравнения Гамильтона — Якоби.
Глава 11.Системы законов сохранения.
Приложение.
Литература.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Уравнения с частными производными, Эванс Л.К., 2003 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу
Учебно-образовательная физико-математическая библиотека
Математическая физика, уравнения с частными производными
- Адамар Ж. Задача Коши для линейных уравнений с частными производными гиперболического типа. М.: Наука, 1978 (djvu, 4.66 M)
- Араманович И.Г., Левин В.И. Уравнения математической физики (2-е изд.). М.: Наука, 1969 (djvu, 3.54 M)
- Бабич В.М., Булдырев В.С. Асимптотические методы в задачах дифракции коротких волн. М.: Наука, 1972 (djvu, 4.71 M)
- Бабич В.М., Кирпичникова Н.Я. Метод пограничного слоя в задачах дифракции. Л.: ЛГУ, 1974 (djvu, 2.02 M)
- Бакельман И.Я. Геометрические методы решения эллиптических уравнений. М.: Наука, 1965 (djvu, 3.12 M)
- Бергман С. Интегральные операторы в теории линейных уравнений с частными производными. М.: Мир, 1964 (djvu, 2.69 M)
- Бернштейн С.Н. Аналитическая природа решений дифференциальных уравнений эллиптического типа. Харьков: ХГУ, 1956 (djvu, 1.22 M)
- Берс Л., Джон Ф., Шехтер М. Уравнения с частными производными. М.: Мир, 1966 (djvu, 6.36 M)
- Брело М. О топологиях и границах в теории потенциала. М.: Мир, 1974 (djvu, 1.48 M)
- Брело М. Основы классической теории потенциала. М.: Мир, 1964 (djvu, 1.30 M)
- Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике (3-е изд.). М.: Наука, 1979 (djvu, 7.45 M)
- Векуа ИН. Новые методы решения эллиптических уравнений. М.-Л. ГИТТЛ, 1948 (djvu, 4.09 M)
- Власова Б.А., Зарубин В.С., Кувыркин Г.Н. Приближенные методы математической физики: Учеб. для вузов. М.: Изд-во МГТУ им. Н.Э. Баумана, 2001 (djvu, 4.90 M)
- Вольперт А.И., Худяев С.И. Анализ в классах разрывных функций и уравнения математической физики. М.: Наука, 1975 (djvu, 4.68 M)
- Гельфанд И.М., Шилов Г.Е. Некоторые вопросы теории дифференциальных уравнений (Обобщенные функции, выпуск 3). М.: Физматлит, 1958 (djvu, 2.39 M)
- Годунов С.К. Уравнения математической физики (2-е изд. ). М.: Наука 1979 (djvu, 6.76 M)
- Годунов С.К., Золотарева Е.В. Сборник задач по уравнениям математической физики. Новосибирск: Наука, 1974 (djvu, 1.98 M)
- Горбузов В.Н. Интегралы дифференциальных систем. Гродно: ГрГУ, 2006 (pdf, 2.68 M)
- Гординг Л. Задача Коши для гиперболических уравнений. М.: ИЛ, 1961 (djvu, 1.23 M)
- Городцов В.А. Софья Ковалевская, Поль Пенлеве и интегрируемость нелинейных уравнений сплошных сред. М.: Физматлит, 2003.
(djvu, 590 K)
- Гурса Э. Курс математического анализа, том 3, часть 1. Бесконечно близкие интегралы. Уравнения с частными производными. М.-Л.: ГТТИ, 1933 (djvu, 4.64 M)
- Гюнтер Н. Теория потенциала и ее применение к основным задачам математической физики. М.: ГИТТЛ, 1953 (djvu, 3.86 M)
- Гюнтер Н.М. Интегрирование уравнений в частных производных первого порядка. Л.-М.: ОНТИ, 1934 (djvu, 4.13 M)
- Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. Приближение функций, дифференциальные и интегральные уравнения. М.: Наука, 1967 (djvu, 5.27 M)
- Егоров Д. Интегрирование дифференциальных уравнений (3-е изд.). М.: Печатня Яковлева, 1913 (djvu, 6.81 M)
- Егоров Д.Ф. Уравнения с частными производными 2-го порядка с двумя независимыми переменными. М.: МГУ, 1899 (djvu, 8.92 M)
- Егоров Ю.В., Шубин М.А., Комеч А.И. Дифференциальные уравнения с частными производными — 2 (серия «Современные проблемы математики», том 31). М.: ВИНИТИ, 1988 (djvu, 3.14 M)
- Зайцев В.Ф., Полянин А.Д. Метод разделения переменных в математической физике. СПб.: Книжный Дом, 2009
(pdf, 1.50 M)
- Зайцев В.Ф., Полянин А.Д. Справочник по дифференциальным уравнениям с частными производными первого порядка. М.: Физматлит, 2003
(djvu, 3.25 M)
- Зайцев Г.А. Алгебраические проблемы математический и теоретической физики. М.: Наука, 1974 (djvu, 1.62 M)
- Заславский Г.М., Сагдеев Р.З. Введение в нелинейную физику: от маятника до турбулентности и хаоса. М.: Наука, 1988 (djvu, 5.09 M)
- Зельдович Я.Б., Мышкис А.Д. Элементы математической физики. Среда из невзаимодействующих частиц. М.: Наука, 1973 (djvu, 4.00 M)
- Зоммерфельд А. Лекции по теоретической физике. Том VI. Дифференциальные уравнения в частных производных физики. М.: ИЛ, 1950 (djvu, 4.87 M)
- Ибрагимов Н.Х. Азбука группового анализа. М.: Знание, 1989 (djvu, 775 K)
- Ибрагимов Н.Х. Группы преобразований в математической физике. М.: Наука, 1983 (djvu, 3.45 M)
- Имшенецкий В.Г. Интегрирование дифференциальных уравнений с частными производными 1-го и 2-го порядков. М.: Изд. Моск. мат. общества, 1916 (djvu, 3.61 M)
- Йон Ф. Плоские волны и сферические средние в применении к дифференциальным уравнениям с частными производными. М.: ИЛ, 1958 (djvu, 2.17 M)
- Калоджеро Ф., Дигасперис А. Спектральные преобразования и солитоны. Методы решения и исследования нелинейных эволюционных уравнений. М.: Мир, 1985 (djvu, 9.28 M)
- Камке Э. Справочник по дифференциальным уравнениям в частных производных первого порядка. М.: Наука, 1966 (djvu, 2.55 M)
- Карпман В.И. Нелинейные волны в диспергирующих средах. М.: Наука, 1973 (djvu, 1.63 M)
- Кирхгоф Г. Механика. Лекции по математической физике. М.: АН СССР, 1962 (djvu, 5.30 M)
- Коллатц Л. Задачи на собственные значения (с техническими приложениями). М.: Наука, 1968 (djvu, 4.89 M)
- Коркин А.Н. Сочинения, том 1. СПб.: Императорская Академия Наук, 1911 (djvu, 3.33 M)
- Кошляков Н.С. Глинер Э.Б. Смирнов М.М. Уравнения в частных производных математической физики. М.: Высшая школа, 1970 (djvu, 14 M)
- Кудряшов Н.А. Аналитическая теория нелинейных дифференциальных уравнений. Москва-Ижевск: Институт компьютерных исследований, 2004 (djvu, 3.01 M)
- Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: Физматлит, 2001 (djvu, 7.29 M)
- Курант Р. Уравнения с частными производными. М.: Мир, 1964 (pdf, 34 M)
- Курант Р., Гильберт Д. Методы математической физики. Том 1. М.-Л.: ГТТИ, 1933 (djvu, 7.17 M)
- Курант Р., Гильберт Д. Методы математической физики. Том 2. М.-Л.: ГТТИ, 1945 (djvu, 9.53 M)
- Куренский М.К. Дифференциальные уравнения. Книга 2. Дифференциальные уравнения с частными производными. Л.: Артиллерийская академия, 1934 (djvu, 5.55 M)
- Лаврентьев М.А. Вариационный метод в краевых задачах для систем уравнений эллиптического типа. М.: АН СССР, 1962 (djvu, 1.27 M)
- Ладыженская О.А. Краевые задачи математической физики. М.: Наука, 1973 (djvu, 3.90 M)
- Ладыженская О.А., Солонников В.А., Уралыдева Н.Н. Линейные и квазилинейные уравнения параболического типа. М.: Наука, 1967 (djvu, 6.04 M)
- Ладыженская О.А., Уральцева Н.Н. Линейные и квазилинейные уравнения эллиптического типа (2-е изд.). М.: Наука, 1973 (djvu, 4.96 M)
- Лакс П., Филлипс Р. Теория рассеяния. М.: Мир, 1971 (djvu, 6.48 M)
- Ландис Е.М. Уравнения второго порядка эллиптического и параболического типов. М.: Наука, 1971 (djvu, 1.91 M)
- Лаптев Г.И., Лаптев Г.Г. Уравнения математической физики. М.: 2003 (pdf, 1.72 M)
- Лионс Ж.-Л. Некоторые методы решения нелинейных краевых задач. М.: Мир, 1972 (djvu, 5.47 M)
- Лионс Ж.-Л. Оптимальное управление системами, описываемыми уравнениями в частных производных. М.: Мир, 1972 (djvu, 5.04 M)
- Лурье А.И. Операционное исчисление и его приложение к задачам механики (2 изд.). ГИТТЛ, 1951.
(djvu, 3.44 M)
- Маделунг Э. Математический аппарат физики: Справочное руководство. М.: Наука, 1968 (djvu, 6.52 M)
- Марченко В.А., Хруслов Е.Я. Краевые задачи в областях с мелкозернистой границей. Киев: Наук. думка, 1974 (djvu, 3.26 M)
- Маслов В.П. Асимптотические методы и теория возмущений. М.: Наука, 1988
(djvu, 3.48 M)
- Маслов В.П., Федорюк М.В. Квазиклассическое приближение для уравнений квантовой механики. М.: Наука, 1976
(djvu, 2.95 M)
- Мизохата С. Теория уравнений с частными производными. М.: Мир, 1977 (djvu, 5.42 M)
- Миллер У. (мл.). Симметрия и разделение переменных. М.: Мир, 1981 (djvu, 4.13 M)
- Миранда К. Уравнения с частными производными эллиптического типа. М.: ИЛ, 1957 (djvu, 2.91 M)
- Михайлов В.П. Дифференциальные уравнения в частных производных.М.: Наука, 1976 (djvu, 3.63 M)
- Михлин С.Г. (ред.). Линейные уравнения математической физики. М.: Наука, 1964 (djvu, 2.74 M)
- Михлин С.Г. Курс математической физики. М.: Наука, 1968 (djvu, 11 M)
- Михлин С.Г. Линейные уравнения в частных производных. М.: Высшая школа, 1977 (djvu, 10 M)
- Морс Ф.М., Фешбах Г. Методы теоретической физики. Том 1. М.: ИЛ, 1958 (djvu, 14 M)
- Морс Ф.М., Фешбах Г. Методы теоретической физики. Том 2. М.: ИЛ, 1960 (djvu, 14 M)
- Нагумо М. Лекции по современной теории уравнений в частных производных. М.: Мир, 1967 (djvu, 1.71 M)
- Назимов П.С. Об интегрировании дифференциальных уравнений. М.: МГУ, 1880 (djvu, 2.82 M)
- Нобл Б. Применение метода Винера — Хопфа для решения дифференциальных уравнений с частными производными. М.: ИЛ, 1962 (djvu, 3.00 M)
- Оганесян Л.А., Руховец Л.А. Вариационно-разностные методы решения эллиптических уравнений, Ереван: АН АрмССР, 1979 (djvu, 11 M)
- Олейник О.А., Иосифьян Г.А., Шамаев А.С. Математические задачи теории сильно неоднородных упругих сред. М.: Изд-во МГУ, 1990
(djvu, 3.08 M)
- Паламодов В.П. Линейные дифференциальные операторы с постоянными коэффициентами. М.: Наука, 1967 (djvu, 4.76 M)
- Петровский И.Г. Лекции об уравнениях с частными производными (3-е изд.). М.: Наука, 1961 (djvu, 7.47 M)
- Полянин А.Д. Справочник по линейным уравнениям математической физики. М.: Физматлит, 2001
(djvu, 4.68 M)
- Полянин А.Д., Журов А.И. Методы разделения переменных и точные решения нелинейных уравнений математической физики. М.: ИПМех РАН, 2020. (ISBN 9785917412580)
(pdf, 4.84 M)
- Полянин А.Д., Зайцев В.Ф. Справочник по нелинейным уравнениям математической физики: Точные решения. М.: Физматлит, 2002
(djvu, 3.45 M)
- Полянин А.Д., Зайцев В.Ф., Журов А.И. Методы решения нелинейных уравнений математической физики и механики. М.: Физматлит, 2005
(djvu, 2.66 M)
- Расулов М.Л. Метод контурного интеграла и его применение к исследованию задач для дифференциальных уравнений. М.: Наука, 1964 (djvu, 4.92 M)
- Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений и их приложения к газовой динамике (2-е изд.) М.: Наука, 1978 (djvu, 5.00 M)
- Салтыков Н.Н. Исследования по теории уравнений с частными производными первого порядка одной неизвестной функции. Харьков, 1904 (djvu, 3.50 M)
- Самарский А.А. Введение в теорию разностных схем. М.: Наука, 1971 (djvu, 5.02 M)
- Синцов Д.М. Теория коннексов в пространстве в связи с теорией дифференциальных уравнений в частных производных первого порядка. Казань: КГУ, 1894 (pdf, 19 M)
- Смирнов М.М. Дифференциальные уравнения в частных производных второго порядка. М.: Наука, 1964 (djvu, 2.85 M)
- Смирнов М.М. Задачи по уравнениям математической физики (6-е изд.). М.: Наука, 1973 (djvu, 1.17 M)
- Смирнов М.М. Уравнения смешанного типа. М.: Наука, 1970 (djvu, 2.96 M)
- Соболев С.Л. Уравнения математической физики (4-е изд.). М.: Наука, 1966 (djvu, 4.51 M)
- Степанов В.В. Курс дифференциальных уравнений (8-е изд.). М.: ГИФМЛ, 1959 (djvu, 5.99 M)
- Тихонов А.Н., Самарский А.А. Уравнения математической физики (5-е изд.). М.: Наука, 1977 (djvu, 7.23 M)
- Трев Ж. Лекции по линейным уравнениям в частных производных с постоянными коэффициентами. М.: Мир, 1965 (djvu, 3.67 M)
- Фещенко С.Ф., Шкиль Н.И., Николенко Л.Д. Асимптотические методы в теории линейных дифференциальных уравнений. Киев: Наукова думка, 1966 (djvu, 2.11 M)
- Фущич В.И., Никитин А.Г. Симметрия уравнений квантовой механики. М.: Наука, 1990 (djvu, 6.77 M)
- Хёрмандер Л. К теории общих дифференциальных операторов в частных производных. М.: ИЛ, 1959 (djvu, 1.34 M)
- Ховратович Д.В. Уравнения математической физики. М.: МГУ, 2003 (pdf, 402 K)
- Шапиро Д.А. Конспект лекций по математическим методам физики. Часть 1 (Уравнения в частных производных. Специальные функции. Асимптотики). Новосибирск: НГУ, 2004 (djvu, 988 K)
- Шапиро Д.А. Конспект лекций по математическим методам физики. Часть 2 (Представления групп и их применение в физике. Функции Грина). Новосибирск: НГУ, 2004 (djvu, 912 K)
- Шилов Г.Е. Математический анализ. Второй специальный курс. М.: Физматлит, 1965 (djvu, 2.58 M)
- Шишмарев И.А. Введение в теорию эллиптических уравнений. М.: МГУ, 1979 (djvu, 2.37 M)
- Шубин М.А. Псевдодифференциальные операторы и спектральная теория (2-е изд.). М.: Добросвет, 2003 (pdf, 2.81 M)
- Яковенко Г.Н., Аксёнов А.В. (ред.). Симметрии дифференциальных уравнений. Сборник научных трудов. М.: МФТИ, 2009 (pdf, 2.49 M)
Число книг в разделе: 106
Научно-образовательный сайт MechMath содержит обширную информацию по математике и механике. Веб-сайт MechMath разработан при поддержке Российского фонда фундаментальных исследований (грант № 09-01-00343) . Адрес веб-сайта: 119526 Москва, пр-т Вернадского, д. 101, корп. 1, Институт проблем механики им. А.Ю. Ишлинского РАН. Дифференциальные уравнения в частных производных с примерами решения и образцами выполненияДифференциальным уравнением с частными производными называется уравнение вида связывающее независимые переменные x1, х2, … , хn искомую функцию и = и(х1, х2,…, хn) и ее частные производные (наличие хотя бы одной производной обязательно). Здесь ki,k2,… ,кn — неотрицательные целые числа, такие, что к1 + к2 + … + кп = т. Порядком дифференциального уравнения называется наивысший порядок входящие в уравнение частных производных. Так, если х, у — независимые переменные, и = и(х, у) — искомая функция, то — дифференциальное уравнение 1-го порядка; — дифференциальные уравнения 2-го порядка. Для упрощения записи пользуются также следующими обозначениями: Пусть имеем дифференциальное уравнение с частными производными (1) порядка т. Обозначим через С m (D) множество функций, непрерывных в области D вместе со всеми производными до порядка m включительно. Определение: Решением дифференциального уравнения (1) в некоторой области D изменения независимых переменных x1, x2…xn,. называется всякая функция и = и(х1, х2,…, xп) ∈ С m (D) такая, что подстановка этой функции и ее производных в уравнение (1) обращает последнее в тождество по x1, x2, …., хп в области D. Пример: Найти решение и = и(х,у) уравнения Равенство (2) означает, что искомая функция и не зависит опт х, но может быть любой функцией от у, u = φ(y). (3) Таким образом, решение (3) уравнения (2) содержит одну произвольную функцию. Это — общее решение уравнения (2). Приме: Найти решение u = u(z, у) уравнения Положим где g(x) — произвольная функция. Так как w(у) — произвольная функция, то и интеграл от нее также является произвольной функцией; обозначим его через f(у). В результате получим решение уравнения (4) в виде u(x, y) = f(y) + g(x) (5) произвольные дифференцируемые функции). Решение (5) уравнения с частными производными 2-го порядка (4) содержит уже две произвольные функции. Его называют общим решением уравнения (4), так как всякое другое решение уравнения (4) может быть получено из (5) подходящим выбором функций f и g. Мы видим, таким образом, что уравнения с частными производными имеют целые семейства решений. Однако существуют уравнения с частными производными, множества решений которых весьма узки и, в некоторых случаях, да же пусты. Пример: Множество действительных решений уравнения исчерпывается функцией u(x, y) = const, а уравнение вовсе не имеет действительных решений. Мы не ставим пока вопрос об отыскании частных решений. Позже будет выяснено, какие дополнительные условия нужно задать, чтобы с их помощью можно было выделить частное решение, т.е. функцию, удовлетворяющую как дифференциальному уравнению, так и этим дополнительным условиям. Линейные дифференциальные уравнения с частными производными. Свойства их решенийУравнение с частными производными называется линейным, если оно линейно относительно искомой функции и всех ее производных, входящих в уравнение; в противном случае уравнение называется нелинейным. Пример: — линейное уравнение; уравнения Линейное дифференциальное уравнение 2-го порядка для функции двух независимых переменных х, у в общем случае имеет вид где А(х, у), В(х, у), …, с(х,у), f(x,y) — функции переменных х, у, заданные в некоторой области D плоскости хОу. Если f(x,y) ≡ 0 в D, то уравнение (1) называется однородным, в противном случае — неоднородным. Обозначив левую часть уравнения (1) через L[u], запишем (1) в виде L[u] = f(x, у). (2) Соответствующее однородное уравнение запишется так: L[u] = 0. (3) Здесь L — линейный дифференциальный оператор, определенный на линейном пространстве C 2 (D) функций и = и(х, у). Пользуясь свойством линейности оператора L, легко убедиться в справедливости следующих теорем, выражающих свойства решений линейных однородных дифференциальных уравнений с частными производными. Теорема: Если и(х, у) есть решение линейного однородного уравнения (3), то си(х, у), где с — любая постоянная, есть также решение уравнения (3). Теорема: Если и1(х, у) и и2(х, у) — решения линейного однородного уравнения (3), то сумма и1(х, у) + и2(x, у) есть также решение этого уравнения. Следствие: Если каждая из функций и1(х, у) и и2(х, у), u k(x, у) является решением уравнения (3), то линейная комбинация где c1, c2 …, сk — произвольные постоянные, также является решением этого уравнения. В отличие от обыкновенного линейного однородного дифференциального уравнения, имеющего конечное число линейно независимых частных решений, линейная комбинация которых дает общее решение этого уравнения, уравнение с частными производными может иметь бесконечное множество линейно независимых частных решений. Пример: имеет общее решение k = φ(х), так что решениями его будут, например, функции 1,х,…, х n ,… . В соответствии с этим в линейных задачах для уравнений с частными производными нам придется иметь дело не только с линейными комбинациями конечного числа решений, но и с рядами Возможны случаи, когда функция и(х, у; λ) при всех значениях параметра λ из некоторого интервала (λо, λ1), конечного или бесконечного, является решением уравнения (3). В этом случае говорят, что решения уравнения зависят от непрерывно меняющегося параметра λ. Если теперь взять функцию С(λ) такую, что первые и вторые производные интеграла по х и по у могут быть получены с помощью дифференцирования под знаком интеграла, то этот интеграл также будет решением уравнения (3). Для линейного неоднородного уравнения L[u] = f (4) справедливы следующие предложения. Теорема: Если и(х, у) есть решение линейного неоднородного уравнения (4), a v(x, у) — решение соответствующего однородного уравнения (3), то сумма и + v есть решение неоднородного уравнения (4). Теорема: Принцип суперпозиции. Если и1(х, у) —решение уравнения L[u] = f1, a u2(x,y) — решение уравнения L[u] = f2, то и1 + u2 — решение уравнения L[u] = f1 + f2. Классификация линейных дифференциальных уравнений второго порядка с двумя независимыми переменнымиОпределение: Линейное дифференциальное уравнение второго порядка в некоторой области Q на плоскости хОу называется 1) гиперболическим в Ω, если 2) параболическим в Ω, если 3) эллиптическим в Ω, если Пользуясь этим определением, легко проверить, что уравнения — гиперболические при всех х и у, уравнение — параболическое при всех х и у, а уравнение — эллиптическое при всех х и у. Уравнение — эллиптическое при у > 0, параболическое на линии у = 0 и гиперболическое в полуплоскости у с помощью которой уравнение (1) преобразуется к более простому, каноническому виду, своему для каждого типа уравнения. Уравнение гиперболического типа (∆ > 0) преобразуется к вшу (два канонических вида уравнений гиперболического типа). Уравнение параболического типа (∆ ≡ 0) преобразуется к виду (канонический вид уравнения параболического типа). Уравнение эллиптического типа (∆ (канонический вид уравнения эллиптического типа). Здесь F и Ф — некоторые функции, зависящие от искомой функции и, ее первых производных В некоторых случаях каноническая форма уравнения позволяет найти общее решение исходного уравнения. Как правило, приведениеуравнения(1) к каноническому виду путем замены независимых переменных имеет локальный характер, т. е. осуществимо лишь в некоторой достаточно малой окрестности рассматриваемой точки Mo(xo, уo). Когда число п независимых переменных больше двух, также различают уравнения гиперболического, параболического и эллиптического типов. Например, при п = 4 простейшая каноническая форма таких уравнений имеет вид Здесь и = и(х, у, z, t). Замечание: В общем случае, когда число независимых переменных больше двух, приведение линейною уравнения с переменными коэффициентами к каноническому виду возможно только в данной точке Мы ограничимся рассмотрением линейных дифференциальных уравнений 2-го порядка. К таким уравнениям приводит большое количество различных физических задач. Так, колебательные процессы различной природы (колебания струн, мембран, акустические колебания газа в трубах, электромагнитные колебания и т. д.) описываются уравнениями гиперболического типа. Простейшим из таких уравнений является уравнение колебаний струны (одномерное волновое уравнение): (2) Здесь х — пространственная координата, t — время, Процессы теплопроводности и диффузии приводят к уравнениям параболического типа. В одномерном случае простейшее уравнение теплопроводности имеет вид Здесь Наконец, установившиеся процессы, когда искомая функция не зависит от времени, определяются уравнениями эллиптического типа, типичным представителем которых является уравнение Лапласа Непосредственной проверкой убеждаемся в том, что решением уравнения (2) является всякая функция и(х, t) вида Можно показать, что решениями уравнения (3) являются функции вида произвольные постоянные, А — числовой параметр). Интегрируя решение и(х, t; λ) = Наконец, нетрудно убедиться, что действительнозначные функции Рn(х,у) и Qn(x, у), определяемые из соотношения являются решениями уравнения Лапласа (4) для п = 0, 1, 2…..Этот последний результат есть частный, случай общего утверждения, что и действительная и мнимая части аналитической функции f(z) = u(x, у) + iv(x, у) комплексного переменного z = х + iy являются решениями уравнения Лапласа (4). В силу линейности уравнения (4) ряды тоже будут решениями уравнения (4), если они сходятся равномерно, как и ряды, полученные из них двукратным почленным дифференцированием по каждому из аргументов х, у. Таким образом, для простейшей — канонической — формы уравнений гиперболического, параболического и эллиптического типов мы располагаем о решениях этих уравнений некоторой информацией. Постановка основных задач для линейных дифференциальных уравнений второго порядкаДля полного описания того или иного физического процесса мало иметь только дифференциальное уравнение процесса, надо еще задать начальное состояние этого процесса (начальные условия) и режим на границе S той области Ω, в которой процесс происходит (граничные условия). Это обусловлено неединственностью решения дифференциальных уравнений. Пример: Общее решение уравнения имеет вид и(х, у) = f(x) + g(y), где f(x) и g(y) — произвольные дифференцируемые функции. Поэтому чтобы выделить решение, описывающее данный физический процесс, необходимо задать дополнительные условия. Различают три основных типа задач для дифференциальных уравнений с частными производными (число независимых переменных равно п): а) задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия, область Ω совпадает со всем пространством R n , граничные условия отсутствуют; б) краевая задача для уравнений эллиптического типа: задаются граничные условия на границе S области Ω, начальные условия отсутствуют; в) смешанная задача для уравнений гиперболического и параболического типов: задаются начальные и граничные условия, Ω ≠ R n Решение заданий и задач по предметам: Дополнительные лекции по высшей математике: Образовательный сайт для студентов и школьников Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника. © Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института источники: http://mechmath.ipmnet.ru/lib/?s=pde http://lfirmal.com/differencialnye-uravneniya-v-chastnyh-proizvodnyh/ |

 (djvu, 590 K)
(djvu, 590 K)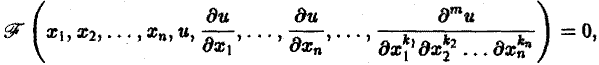
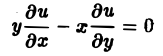
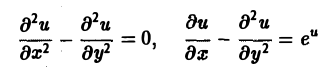
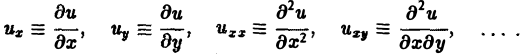


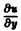 = о. Тогда уравнение (4) примет вид
= о. Тогда уравнение (4) примет вид 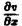 = 0. Его общим решением будет произвольная функция v = w(у). Поскольку v=
= 0. Его общим решением будет произвольная функция v = w(у). Поскольку v= 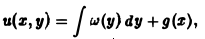
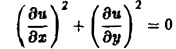
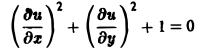

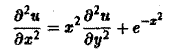
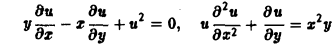
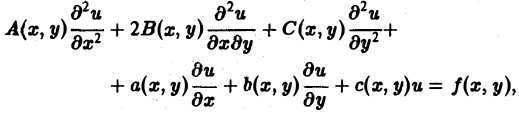
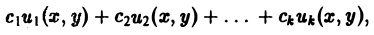
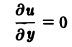
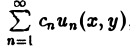 , членами которых являются произведения постоянных Сп на частные решения иn(х, у) дифференциального уравнения.
, членами которых являются произведения постоянных Сп на частные решения иn(х, у) дифференциального уравнения.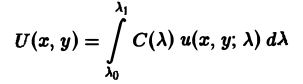
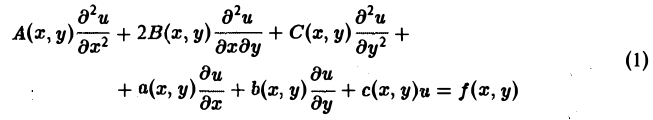
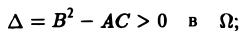
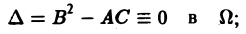
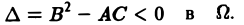

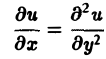
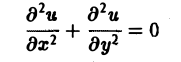
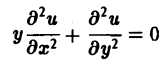
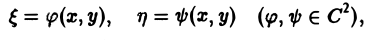
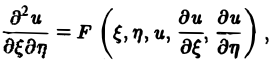
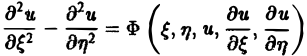
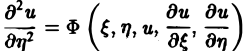
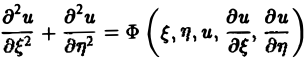
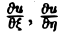 и независимых переменных ξ, η. Вид функций F и Ф определяется исходным уравнением (1).
и независимых переменных ξ, η. Вид функций F и Ф определяется исходным уравнением (1).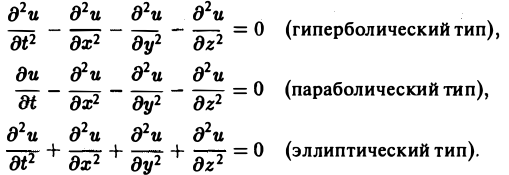
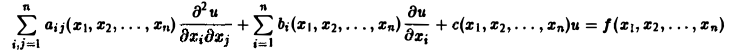
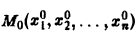 и невозможно в любой сколь угодно малой окрестности этой точки.
и невозможно в любой сколь угодно малой окрестности этой точки.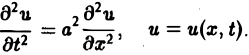
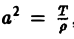 где Т — натяжение струны, р — ее линейная плотность.
где Т — натяжение струны, р — ее линейная плотность.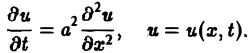
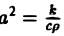 где р — плотность среды, с — удельная теплоемкость, k — коэффициент теплопроводности.
где р — плотность среды, с — удельная теплоемкость, k — коэффициент теплопроводности.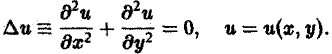
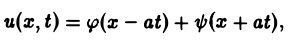
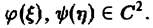
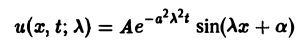
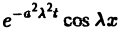 уравнения (3) по параметру λ в пределах от — ∞ до + ∞ , получим так называемое фундаментальное решение U(x, t) =
уравнения (3) по параметру λ в пределах от — ∞ до + ∞ , получим так называемое фундаментальное решение U(x, t) = 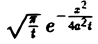 уравнения теплопроводности.
уравнения теплопроводности.