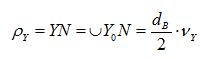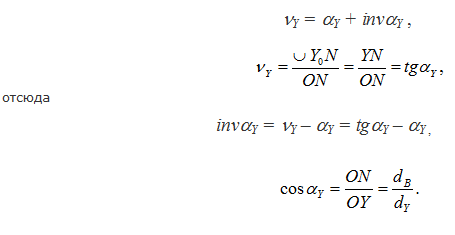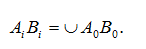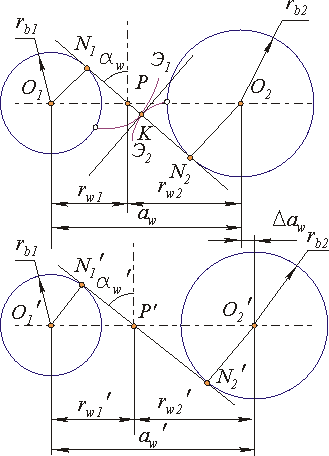Эвольвента ее уравнения и свойства прикладная механика

Теория машин и механизмов (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7

Министерство образования Российской Федерации

Южно-Уральский государственный университет

Филиал в г. Златоусте

Кафедра технической механики

ТЕОРИЯ МАШИН И МЕХАНИЗМОВ

, Зизин машин и механизмов: Курс лекций. ¾ Челябинск: Изд-во ЮУрГУ, 2004. –– Ч. 2. ¾ 100 с.

Курс лекций предназначен для самостоятельного изучения разделов дисциплины «Теория механизмов и машин»: «Синтез механизмов», «Динамический анализ механизмов».

В курсе изложены основные теоретические положения синтеза механизмов с высшими кинематическими парами, приводятся общие сведения о силах трения, причинах износа и способах борьбы с износом, сведения о надежности и качестве машин, способах прогнозирования надежности. Также изложены принципы виброизоляции и виброзащиты механизмов, методы расчета и измерения КПД машин.

Курс лекций предназначен для студентов машиностроительных специальностей.

Ил. 64, список лит. – 5 назв.

Одобрено учебно-методической комиссией филиала ЮУрГУ в г. Златоусте.

Ó Издательство ЮУрГУ, 2004.

В настоящее время почти нет машин и механизмов, в которых не было бы передачи зацеплением. Широкое распространение таких передач объясняется надежностью их в работе и высокой несущей способностью. Правильно рассчитанные зубчатые и червячные передачи могут работать теоретически неограниченное, а практически очень длительное время.

В Российской Федерации проводятся большие исследовательские работы в области усталостной прочности зубчатых колес, динамических процессов в зубчатых передачах, концентрации нагрузки по контактным линиям, заедания рабочих поверхностей и многие другие.

Значительное развитие получили исследования в области точности зубчатых и червячных передач, а также снижения шума при работе зубчатых колес. Пересмотрены Государственные стандарты на точность изготовления зубчатых и червячных передач. Освоены производством новые разновидности и даже новые виды передач зацеплением, отличающиеся высокой несущей способностью и хорошими эксплуатационными показателями. Сюда относятся червячные передачи с червяками, имеющими вогнутый профиль, дозаполюсные передачи Новикова и др.

Работа над новыми видами передач, в свою очередь, способствует выявлению скрытых запасов прочности в передачах существующих видов, возможности повышения несущей способности которых, казалось, были исчерпаны.

Однако, если в изучении геометрии зубчатых и червячных передач достигнуты большие успехи и имеется большой прогресс в области их изготовления, то физическая сущность явлений, происходящих в контакте зубьев и в разделяющем их масляном слое, во многом еще не ясна. Зависимости, которые приходится использовать для расчета зубьев на прочность, еще далеки от совершенства. По мере накопления опыта эти зависимости меняются и уточняются.

Экспериментальные исследования не подчинены единому плану, в результате чего некоторые вопросы расчета изучаются достаточно подробно, другие же, значительно более актуальные, как, например, расчет на излом косых зубьев, исследование контактной выносливости зубьев при точечном касании и др., остаются почти незатронутыми. Число экспериментов в каждом исследовании часто слишком мало, чтобы служить основой уверенных количественных рекомендаций, а при усталостных испытаниях –– иногда даже качественных. Этим объясняются встречающиеся противоречия в оценке различными исследователями влияния того или иного фактора. Только широко развернутые эксперименты и систематический направленный сбор статистических данных о работе зубчатых передач в промышленности позволят применить теорию вероятностей к расчету передач зацеплением.

Все изложенное является основной причиной того, что, несмотря на решения ряда технических совещаний и конференций по зубчатым передачам, еще не создан единый метод расчета передач зацеплением.

Недостаточное внимание уделяется пока и такому важному фактору, как определение величины и характера нагрузок, с которыми должны работать передачи. Исходные данные для расчета часто выбираются необоснованно, а нагрузки из осторожности назначаются с неоправданным запасом, вследствие чего уточненный расчет передачи теряет всякий смысл. Накапливание сведений о действительных нагрузках, с которыми работают детали различных машин, и изучение специфических условий работы этих деталей являются одной из важнейших проблем в деятельности проектно-конструкторских организаций и СКБ заводов.

1. КЛАССИФИКАЦИЯ ЗУБЧАТЫХ ПЕРЕДАЧ

Бытующие в технической литературе наименования различных типов зубчатых передач получили широкое распространение, но зачастую недостаточно четки. С другой стороны, многие предлагаемые системы классификации страдают излишней академичностью и не получили признания. В связи с этим наиболее правильным будет принять компромиссное решение.

Приведенная на рис. 1 классификация зубчатых передач представляет часть общей классификации, предложенной , и включает лишь те виды зубчатых передач, которые применяются в промышленности или достаточно перспективны. Наряду с терминологией, подчиненной схеме, приводятся названия передач, получившие распространение в инженерной практике.

Передачи внешнего зацепления

Характерной особенностью кинематики передач с внешним зацеплением является то, что ведущее и ведомое звенья имеют разное направление вращения.

Цилиндрические эвольвентные зубчатые передачи с линейным касанием

Прямозубые цилиндрические колеса показаны на рис. 2. Зубья таких колес параллельны оси и имеют одинаковый профиль от одного до другого торца. Нефланкированные эвольвентные прямозубые колеса применяются обычно при окружных скоростях до 5…7 м/с. При больших окружных скоростях для спокойной работы передачи требуется фланкировать зубья или изготавливать их с повышенной точностью. Как правило, в этом случае более рентабельным будет переход на косозубую передачу.

Косозубые эвольвентные цилиндрические колеса (рис. 3) отличаются от прямозубых тем, что направление зубьев составляет некоторый угол с образующей делительного цилиндра. Вследствие более плавной работы косозубые колеса могут быть использованы при более высоких окружных скоростях. Недостатком косозубых колес является то, что в зацеплении возникает осевая составляющая передаваемой зубьями силы, воспринимаемая одной из опор каждого вала, чего нет в прямозубых колесах.

Рис. 1. Классификация зубчатых передач

Рис. 2. Прямозубые цилиндрические колеса

Рис. 3. Косозубая цилиндрическая шестерня

Шевронные эвольвентные цилиндрические колеса показаны на рис. 4 и 5. Правые и левые половины шевронных зубчатых колес имеют разное направление зубьев, вследствие чего осевая составляющая в шевронных передачах сводится к силе трения в опорах, возникающей при незначительных осевых перемещениях («игре») шевронных зубчатых колес во время работы. Шевронные колеса применяются обычно для мощных зубчатых передач, работающих со средними и высокими окружными скоростями. Различают шевронные зубчатые колеса с дорожкой (канавкой) в середине колеса (см. рис. 4) для выхода инструмента (червячной фрезы) и без дорожки (см. рис. 5), нарезаемые долбяком или гребенкой со специальной формой заточки. Шеврон без дорожки обладает высокой прочностью зубьев на излом, но применяется реже, чем шеврон с дорожкой.

Зубчатые передачи с зацеплением Новикова (рис. 6) характеризуются более высокой, чем у эвольвентной зубчатой передачи, контактной прочностью. Передачи Новикова могут выполняться с параллельными, пересекающимися и перекрещивающимися осями, однако, в основном применяются передачи с параллельными осями. Профили зубьев передачи Новикова очерчены дугами окружностей (обычно в нормальном сечении), причем выпуклые зубья одного зубчатого колеса (обычно шестерни) контактируют с вогнутыми зубьями другого. Без нагрузки рабочие поверхности зубьев касаются в точке. Под нагрузкой точка превращается в контактную площадку, как у эвольвентных зубчатых колес с бочкообразными зубьями.

Линией зацепления является прямая, расположенная параллельно осям зубчатых колес. Соприкосновение зубьев парных зубчатых колес в каждой торцовой плоскости происходит только в одной точке, в связи с чем передачи Новикова выполняются только с непрямыми (косыми или шевронными) зубьями и осевым коэффициентом перекрытия, большим единицы. При работе контактная площадка перемещается вдоль зуба, что создает благоприятные условия для возникновения между зубьями устойчивой масляной пленки. Потери на трение в зацеплении Новикова меньше, чем в эвольвентной передаче, стойкость в отношении абразивного изнашивания –– меньшая.

Зубчатые колеса с зацеплением Новикова нарезаются на тех же зуборезных станках, что и эвольвентные зубчатые колеса. Минимальное число зубьев не ограничено подрезанием, как у эвольвентных зубчатых колес, поэтому передачу Новикова можно осуществить с большими передаточными числами, чем эвольвентную, при той же несущей способности из условия контактной прочности.

iSopromat.ru

Эвольвентное зацепление зубчатых колес удовлетворяет основному закону зацепления, обеспечивает постоянство передаточного отношения, допускает отклонение межосевого расстояния зубчатых передач и точно стандартизируется.

Подавляющее большинство зубчатых передач, применяемых в технике, имеет зубчатые колеса с эвольвентным профилем.

Эвольвента как кривая для формирования профиля зуба была предложена Л. Эйлером. Она обладает значительными преимуществами перед другими кривыми, применяемыми для этой цели, – удовлетворяет основному закону зацепления, обеспечивает постоянство передаточного отношения, нечувствительна к неточностям межосевого расстояния (что облегчает сборку), наиболее проста и технологична в изготовлении, легко стандартизируется (что особенно важно для такого распространенного вида механизмов как зубчатые передачи).

На следующем видео показан пример эвольвентного зацепления зубчатых колес

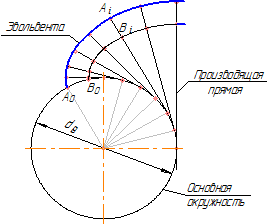
Эвольвента – это траектория движения точки, принадлежащей прямой, перекатывающейся без скольжения по окружности. Данная прямая называется производящей прямой, а окружность, по которой она перекатывается – основной окружностью (рисунок 38 а).

Эвольвента обладает следующими свойствами, которые используются в теории зацепления:

1. форма эвольвенты определяется радиусом основной окружности;
2. нормаль к эвольвенте в любой ее точке является касательной к основной окружности. Точка касания нормали с основной окружностью является центром кривизны эвольвенты в рассматриваемой точке;
3. эвольвенты одной и той же основной окружности являются эквидистантными (равноотстоящими друг от друга) кривыми.

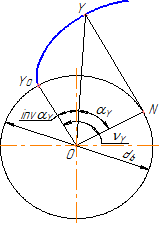
Положение любой точки на эвольвенте может быть однозначно охарактеризовано диаметром окружности, на которой она расположена, а также характерными для эвольвенты углами: углом развернутости (обозначается ν ), углом профиля ( α ), эвольвентным углом – inv α (рисунок 38 б). На рисунке 38 б показаны эти углы для произвольно выбранной на эвольвенте точки Y, поэтому они имеют соответствующий индекс:

• ν _Y – угол развернутости эвольвенты до точки у;
• α _Y – угол профиля в точке Y;
• inv α _Y – эвольвентный угол в точке Y (на окружности диаметра dY ).

То есть индекс показывает, на какой окружности находится рассматриваемая точка эвольвенты, поэтому для характерных окружностей используются индексы, приведенные выше.

Например: α _a1 – угол профиля эвольвенты в точке, лежащей на окружности вершин первого колеса;
inv α – эвольвентный угол в точке эвольвенты, находящейся на делительной окружности колеса и т.д.

Рассмотрим свойства эвольвенты. Первое свойство имеет строгое математическое доказательство, однако в рамках данного короткого курса оно не приводится.

Так как при формировании эвольвенты производящая прямая перекатывается по основной окружности без скольжения, то в данный момент времени она вращается вокруг точки N (N – мгновенный центр скоростей), описывая бесконечно малую дугу окружности, которая и определяет кривизну эвольвенты в данной точке. Т.е. отрезок NY – это радиус кривизны эвольвенты в точке Y (NY= ρ _Y).

Но отрезок NY в точности равен дуге NY₀ (это та же дуга только вытянутая в прямую линию). Таким образом, имеем:

Чем больше радиус основной окружности, тем больше радиус кривизны эвольвенты в любой ее точке (то есть форма эвольвенты действительно определяется величиной радиуса основной окружности).

Второе свойство также легко просматривается. Так как N – мгновенный центр скоростей, то скорость точки Y перпендикулярна радиусу NY. Но скорость точки, движущейся по криволинейной траектории, направлена по касательной к этой траектории – в данном случае по касательной к эвольвенте в точке Y.

Перпендикуляр к касательной – есть нормаль, поэтому прямая YN с одной стороны является нормалью к эвольвенте в точке Y, с другой стороны является касательной к основной окружности (как производящая прямая, перекатывающаяся по основной окружности).

То, что точка N является центром кривизны эвольвенты в точке Y, показано при рассмотрении первого свойства. Запишем некоторые зависимости, которые используются в дальнейшем при изучении геометрии эвольвентного зацепления (получаются из рассмотрения рисунка 38 б):

Третье свойство эвольвенты очевидно из рисунка 38а. Действительно, если на производящей прямой взять две точки (А и В), то они будут описывать две совершенно одинаковых эвольвенты, причем, как бы не перемещалась производящая прямая, расстояние между этими точками не изменяется (A_iB_i = Const). Т.е. действительно это эквидистантные (равноотстоящие друг от друга) кривые. Но, самое важное, что это расстояние A_iB_i равно расстоянию между этими эвольвентами, измеренному по дуге основной окружности:

Признаком того, что два криволинейных профиля касаются (а не пересекаются), является наличие у них в точке контакта общей нормали. В связи с этим контакт двух эвольвентных профилей происходит на общей касательной к основным окружностям N₁N₂ (рисунок 39), которая одновременно будет являться общей нормалью к этим профилям в точке их касания в любой момент времени (на основании второго свойства эвольвенты).

Геометрическое место точек контакта профилей, которое они занимают в процессе работы пары зубьев, называется линией зацепления. Таким образом, в эвольвентной передаче линией зацепления является прямая N₁N₂ (общая касательная к основным окружностям).

На рисунке 39 а показано зацепление двух эвольвентных профилей в разные моменты времени. В обоих положениях прямая N₁N₂ является общей нормалью к этим касающимся профилям и проходит через полюс зацепления W (мгновенный центр относительного вращения).

Это, с одной стороны показывает, что эвольвентные профили удовлетворяют основному закону зацепления, с другой стороны обеспечивают постоянство передаточного отношения, т.к. полюс зацепления не меняет своего положения в процессе работы пары (отношение O₂W/O₁W остается постянным).

С изменением межосевого расстояния будет меняться только положение линии зацепления, но вся картина зацепления останется такой же, т.е. по-прежнему будет сохраняться основной закон зацепления, величина и постоянство передаточного отношения. Это очень важное свойство эвольвентного зацепления, т.к. позволяет вписывать передачу в разные межосевые расстояния, что особенно важно при проектировании коробок скоростей, планетарных и дифференциальных механизмов.

Передача оказывается малочувствительной к неточностям межосевого расстояния, что позволяет снизить требования к точности сборки.

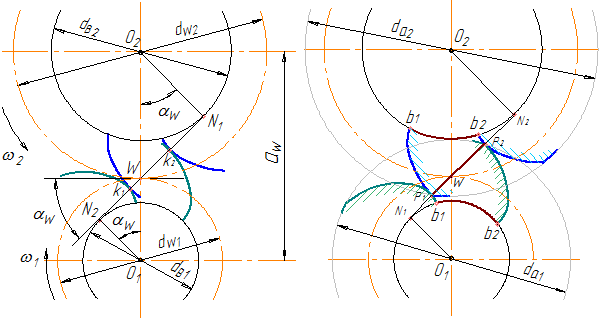
Угол между линией зацепления и общей касательной к начальным окружностям в полюсе называется углом зацепления. Угол зацепления, угол профиля на начальной окружности первого колеса и угол профиля на начальной окружности второго колеса равны между собой (α_w1=α_w2=α_w) , поэтому все они обозначаются одинаково – α_w (без числового индекса – см. рисунок 39 а).

Отрезок N₁N₂ называется теоретической линией зацепления. На этом участке происходит нормальная работа двух неограниченных эвольвент.

В реальной передаче эвольвенты ограничены («обрезаны») окружностями вершин, поэтому вся работа пары происходит на участке линии зацепления P₁P₂, заключенном между окружностями вершин (рисунок 39б).

Отрезок P₁P₂ называется рабочей (активной) частью линии зацепления (иногда называют просто «рабочая линия зацепления», или «активная линия зацепления»). На рисунке 39б показано два положения одной и той же пары: в начале зацепления (зуб ведомого колеса работает своей вершиной, зуб ведущего колеса – нижней рабочей точкой профиля Р₁), и в конце зацепления (зуб ведущего колеса работает своей вершиной и в следующий момент выйдет из зацепления, зуб ведомого колеса работает своей нижней рабочей точкой профиля Р₂).

Примечание: здесь термин «нижняя» или «верхняя» точка относится к положению точек относительно основной окружности, независимо от того, как эти точки располагаются одна относительно другой в пространстве. Из двух рассматриваемых точек профиля «нижней» будет та, которая располагается ближе к основной окружности.

При увеличении радиуса основной окружности до бесконечности радиус кривизны эвольвенты в любой ее точке также становится бесконечно большим, т.е. основная окружность и эвольвента превращаются в прямые линии. Эвольвентное зубчатое колесо превращается в зубчатую рейку с прямолинейным профилем зуба.

Таким образом, рейка с прямолинейным профилем зуба представляет собой частный случай эвольвентного зубчатого колеса и обладает всеми его свойствами, т.е. может работать с любым эвольвентным колесом (при одном и том же модуле) без нарушения основного закона зацепления. При этом вращательное движение колеса преобразуется в поступательное движение рейки или поступательное движение рейки преобразуется во вращательное движение колеса с соблюдением постоянства передаточного отношения.

Т.к. зубчатая рейка с прямолинейным профилем зуба с одной стороны имеет простые формы и легко задать размеры ее элементов, с другой стороны представляет собой эвольвентное зубчатое колесо, то ее параметры положены в основу стандартизации эвольвентных зубчатых колес. Стандартная зубчатая рейка называется исходным контуром (рисунок 40а).

Имеется несколько стандартов на исходные контуры, учитывающие специфику некоторых видов передач (мелкомодульных, конических и т.д.). В основном используются параметры, определенные ГОСТ 13 755 – 81.

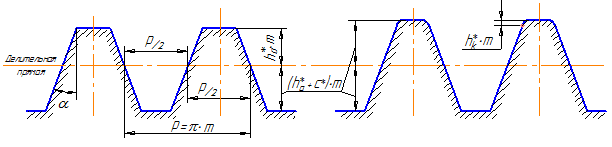
В соответствии с этим стандартом исходный контур имеет следующие параметры:

• α = 20 0 – угол профиля исходного контура (основной параметр, определяющий ряд эвольвент, используемых для зубчатых передач в соответствии с этим стандартом, поэтому часто в конструкторской практике говорят, что у нас в стране используется «двадцатиградусная» эвольвента);
• h_a * = 1 – коэффициент высоты головки зуба;
• c*= 0,25 – коэффициент радиального зазора (по другим стандартам в зависимости от модуля и типа инструмента с* может быть равен 0,2; 0,3; 0,35);

Приведенные коэффициенты являются безразмерными величинами. Абсолютное значение какого-либо размера получается умножением соответствующего коэффициента на модуль (Например: высота головки зуба h_a=h_a * ∙m; величина радиального зазора c = c*∙m и т. д.).

Таким образом, форма зуба остается постоянной, а абсолютные размеры определяются модулем (т.е. модуль является как бы коэффициентом пропорциональности).

По высоте зуб исходного контура делится на головку и ножку. Это деление осуществляется делительной прямой. Делительная прямая рейки – это прямая, на которой толщина зуба равна ширине впадины (рисунок 40б).

Высота ножки зуба несколько больше головки для обеспечения радиального зазора между вершинами зубьев одного колеса и окружностью впадин другого после сборки передачи.

Стандартные параметры исходного контура на эвольвентное колесо «переносятся» через делительную окружность (на делительной окружности шаг равен стандартному шагу исходного контура p= π ∙ m, угол профиля равен углу профиля исходного контура α = 20 0 ).

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Эвольвента окружности и ее свойства

Эвольвента окружности – это кривая, центры кривизны которой лежат на окружности. Эвольвенту окружности (рис. 2), которую описывает точка прямой , можно получить, если прямую перекатыватьбез скольженияпо окружности радиуса . Эта окружность называется основной.

Основные свойства эвольвенты:

а) радиус кривизны в произвольной точке равен и, следовательно, центр кривизны любой точки эвольвенты лежит на основной окружности;

б) радиус кривизны нормален к эвольвенте в точке и касается основной окружности в точке ;

в) длина касательной равна длине дуги ;

г) эвольвента не имеет точек внутри основной окружности.

Уравнения эвольвенты в параметрической форме (параметр угол 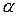, рис. 2) имеют вид:

, .

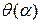
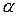
Функцию называют эвольвентной функцией и сокращенно пишут (инволюта ) т.е.

.

4. Эвольвентное зацепление и его свойства

В зубчатой передаче контактирующие элементы двух профилей выполняются по эвольвентам окружности и образуют, так называемое эвольвентное зацепление. Это зацепление обладает рядом полезных свойств, которые и определяют широкое распространение эвольвентных зубчатых передач в современном машиностроении.

Свойство 1. Передаточное отношение эвольвентного зацепления определяется только отношением радиусов основных окружностей и является величиной постоянной:

Свойство 2. При изменении межосевого расстояния в эвольвентном зацеплении его передаточное отношение не изменяется.

Свойство 3. При изменении межосевого расстояния в эвольвентном зацеплении величина произведения межосевого расстояния на косинус угла зацепления не изменяется.

Свойство 4. За пределами отрезка линии зацепления N₁N₂ рассматриваемые ветви эвольвент не имеют общей нормали, т. е. профили, выполненные по этим кривым, будут не касаться, а пересекаться. Это явление называется интерференцией эвольвент или заклиниванием.

5. Геометрические параметры эвольвентного зубчатого колеса

Эвольвентным зубчатым колесом называют звено зубчатого механизма, снабженное замкнутой системой зубьев. Основные геометрические параметры эвольвентного зубчатого колеса показаны на рис. 4. В инженерных расчетах для определения геометрических размеров зубчатых колес используется некоторый параметр, называемый модулем зацепления.

Модулем зацепления называется линейная величина в p раз меньшая окружного шага или отношение шага по любой концентрической окружности зубчатого колеса к p: .

Модуль можно определить как число миллиметров диаметра, приходящееся на один зуб. В зависимости от окружности, по которой определен модуль, различают делительный, основной, начальный. ГОСТом введен стандартный ряд модулей. Стандартный модуль определяется по окружности, называемой делительной.

Делительной называется такая окружность зубчатого колеса, на которой модуль и шаг принимают стандартное значение. Делительная окружность делит зуб на головку и ножку. Радиус делительной окружности согласно ГОСТ обозначается r.

Окружность вершин (r_a) — очерчиваетвершины зубьев.

Окружность впадин (r_f) — очерчивает ножки зубьев.

Основная окружноcть (r_b) – это окружность, по которой перекатывается нормаль .

Окружным шагом или шагом называется расстояние по дуге окружности между одноименными точками профилей соседних зубьев (под одноименными понимаются правые или левые профили зуба).

Угловой шаг t — центральный угол, соответствующий дуге p —окружному шагу.

Углом профиля a называется острый угол между касательной к профилю в данной точке и радиусом — вектором, проведенным в данную точку из центра колеса.

Шаг колеса делится на толщину зуба s_yи ширину впадины e_y.

Толщина зуба s_y— расстояние по дуге окружности r_yмежду разноименными точками профилей зуба.

Ширина впадины e_y— расстояние по дуге окружности r_yмежду разноименными точками профилей соседних зубьев.

В зависимости от соотношения между толщиной зуба и шириной впадины на делительной окружности зубчатые колеса делятся на: нулевые s = e

положительные s > e;отрицательные s