Факторы спроса в уравнении регрессии

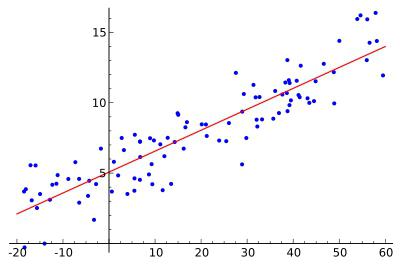
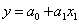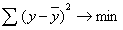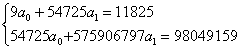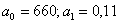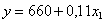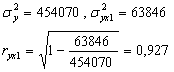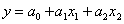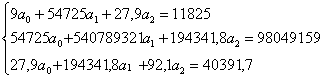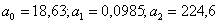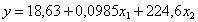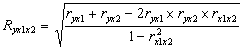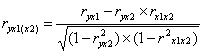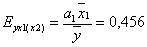Регрессионная модель спроса

Рассмотрим сначала однофакторную линейную модель зависимости расходов на питание от душевого дохода семей, она выражается линейной функцией вида

Параметры уравнения находятся в результате решения системы нормальных уравнений, которая в свою очередь формируется с применением метода наименьших квадратов, предложенного французским математиком Лежандором. Сумма квадратов отклонений должна быть минимальна согласно методу наименьших отклонений, т.е.

Система нормальных уравнений для рассматриваемого случая имеет вид:

уравнение регрессии имеет вид

Направление связи между у и х1определяет знак коэффициента регрессии. В нашем случае связь является прямой. Теснота этой связи определяется коэффициентом корреляции, чем ближе значение коэффициента корреляции к единице, тем теснее корреляционная связь. В нашем случае

Полученное значение коэффициента корреляции свидетельствует, что связь между расходами на питание и душевым доходом очень тесная.

Величина 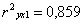называется коэффициентом детерминации и показывает долю изменения результативного признака под воздействием факторного признака, т.е. 86% изменения расходов на питание можно объяснить фактором душевого дохода.

Теперь рассмотрим двухфакторную линейную модель зависимости расходов на питание от душевого дохода семей и размера семей.

Многофакторный корреляционно – регрессионный анализ решает три задачи: определяет форму связи результативного признака с факторными, выявляет тесноту этой связи и устанавливает влияние отдельных факторов.

В нашем случае модель имеет вид

Параметры, находятся в результате решения системы нормальных уравнений

Решая систему, получим

Тогда уравнение регрессии имеет вид

Для определения тесноты связи предварительно вычисляются парные коэффициенты корреляции. После этого вычисляется коэффициент множественной корреляции:

который колеблется в пределах от 0 до 1; чем ближе он к единице, тем в большей степени учтены факторы, влияющие на результативный признак. А в нашем примере Ryx1x2 = 0, 983, что выше значения коэффициента корреляции в случае однофакторной регрессии. Таким образом, связь расходов на питание с факторами душевого дохода и размера семей является очень тесной.

Величина 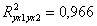называется совокупным коэффициентом детерминации и показывает долю вариации результативного признака под воздействием факторных признаков, т.е.97% изменения расходов на питание можно объяснить факторами душевого дохода и размера семей.

Задача анализа тесноты связи между результативным и одним из факторных признаков при неизменных значениях других факторов решается в многофакторных моделях при помощи частных коэффициентов корреляции. Так частный коэффициент корреляции между результативным признаком и факторным признаком при неизменном значении факторного признака рассчитывается по формуле

где используются парные коэффициенты корреляции. Для рассматриваемого примера частные коэффициенты расходов на питание от душевого дохода и размера семей составляют , 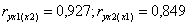т.е. теснота связи между расходами на питание и одним из исследуемых факторов при неизменном значении другого весьма велика.

Если частные коэффициенты корреляции возвести в квадрат, то получим частные коэффициенты детерминации, показывающие долю вариации результативного признака под действием одного из факторов при неизменном значении другого фактора. В нашем примере 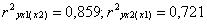следовательно, влиянием душевого при неизменном размере семьи объясняется почти 86% изменения расходов на питание, а изменение размера семьи при неизменном душевом доходе объясняет более 72% изменения расходов на питание.

Влияние отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью частных коэффициентов эластичности, которые показывают, на сколько процентов изменится результативный признак, если значение одного из факторных признаков изменится на 1%, а значение другого факторного признака останется неизменным.

В случае линейной двухфакторной модели частные коэффициенты эластичности рассчитываются по формулам:

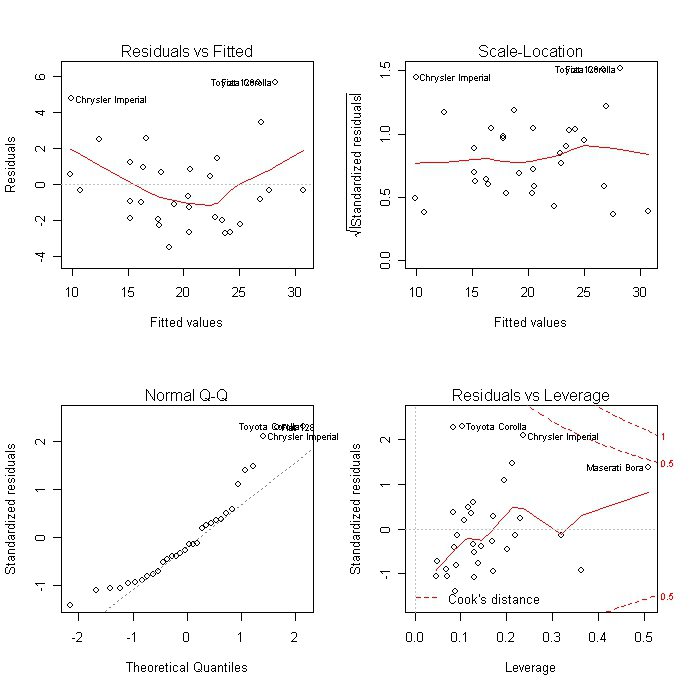
Это означает, что при увеличении душевого дохода на 1% и неизменном размере семьи расходы на питание увеличатся на 0,456%, а увеличение (условное) на один процент размера семьи при неизменном душевом доходе приведет к возрастанию расходов на питание на 0,530%.

Исследование функции спроса методом эконометрического моделирования

Исследование функции спроса методом эконометрического моделирования

Федеральное агентство по образованию

Т О М С К И Й П О Л И Т Е Х Н И Ч Е С К И Й У Н И В Е Р С И Т Е Т

« ­­­_____ » _______________ 2009 г.

ИССЛЕДОВАНИЕ ФУНКЦИИ СПРОСА

МЕТОДОМ ЭКОНОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ

методические указания по курсу

для студентов специальности 080116«Математические методы в экономике»

ИССЛЕДОВАНИЕ ФУНКЦИИ СПРОСА МЕТОДОМ
ЭКОНОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ

Mетодические указания по курсу методические указания по курсу

для студентов специальности 080116«Математические методы в экономике»

— Томск: Изд. ТПУ, 20с.

Методические указания обсуждены на заседании кафедры прикладной математики 23.05.2008 г.

1. Изучение функции спроса с помощью метода эконометрического моделирования.

1.1. Построение математических моделей функции спроса с помощью аппарата парного регрессионного анализа.

1.2. Построение математических моделей функции спроса с помощью аппарата множественного регрессионного анализа.

2. Примеры исследования элементов эконометрического анализа для построения регрессионных моделей.

2.1. Построение линейной парной регрессионной модели.

2.2. Построение линейной множественной регрессионной модели.

3. Оценка значимости уравнения регрессии. Коэффициент детерминации.

4. Оценка значимости множественной регрессии. Коэффициенты детерминации R2 и R2.

1. Изучение функции спроса с помощью метода эконометрического моделирования.

1.1. Построение математических моделей функции спроса с помощью аппарата парного регрессионного анализа.

К так называемым парным зависимостям типа y=f(x) относится подавляющее большинство всех формул, используемых в естественнонаучных и технических дисциплинах. По результатам экспериментов такие формулы обычно строили, применяя метод наименьших квадратов, однако только с появлением новейших ЭВМ, пригодных для выполнения расчётов очень большого объёма, удаётся построить парные зависимости оптимальной формы.

Сама по себе процедура линейного парного регрессионного анализа (метода наименьших квадратов на плоскости) очень проста. Пусть имеется n пар наблюдений значений функции отклика yi , полученных при фиксированных (в смысле записанных) значениях независимой переменной фактора xi. Для графического изображения этих пар наблюдений в виде экспериментальных точек с координатами (х; у) на плоскости применяется система декартовых координат.

Задача линейного регрессионного анализа (метода наименьших квадратов) состоит в том, чтобы, зная положения точек на плоскости, так провести линию регрессии, чтобы сумма квадратов отклонений S, вдоль оси Оу (ординаты) была минимальной.

Для проведения вычислений по классическому методу наименьших квадратов (для проведения регрессионного анализа) предъявляется такое требование: это уравнение должно быть линейным по параметрам или допускать возможность линеаризации. Так, например, процедура проведения регрессионного анализа одинакова для уравнений y=a0+ a1x и y=a0+a1z2, так как подстановка x=z2 приводит второе уравнение к первому.

Уравнение прямой на плоскости в декартовых координатах:

(1.1.) Задачу МНК для данного уравнения аналитически можно выразить следующим образом:

(1.2)

Запишем систему нормальных уравнений, где выполнена операция дифференцирования:

(1.3)

Преобразуем полученную систему нормальных уравнений:

(1.4)

Из первого уравнения системы выразим коэффициент а0 следующим образом:

(1.5)

Подставим (1.5) во второе уравнение (1.4) и найдём коэффициент а1.

И разделив числитель и знаменатель правой части на n, получим запись уравнения с использованием средних:

(1.6)

Как известно из теории вероятности оценка дисперсии равна среднему квадратов значений переменной минус квадрат общей средней:

(1.7)

(1.8)

Оценка дисперсии показывает рассеяние возможных значений случайной величины вокруг её среднего значения. Она имеет размерность, равную квадрату размерности случайной величины, поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение для х и для у, а не дисперсию. Учитывая выше сказанное, подставим (1.7) в выражение (1.6) и умножим правую и левую части полученного уравнения на :

(1.9)

Правая часть уравнения (1.9) является оценкой коэффициента корреляции r, который используется для определения степени взаимосвязи между двумя случайными величинами (количественная характеристика зависимости случайных величин):

(1.10)

Когда связь функциональная, понятие корреляции практически не имеет смысла (коэффициент парной корреляции всегда равен -1 или 1). Для статистической связи вычисление коэффициента парной корреляции r между у и х его статистическая оценка – важная процедура, результаты проведения которой позволяют судить о тесноте связи.

Коэффициент r может изменяться от -1 до 1. Чем ближе r к 1, тем ближе изучаемая зависимость к функциональной. Если, например, коэффициент r- величина отрицательная, то это значит, что х уменьшается с увеличением у. Если r положителен, то х увеличивается с увеличением у. Коэффициент r равен нулю тогда и только тогда, когда линия регрессии у по х представляет собой горизонтальную прямую, проходящую через центр распределения, т. е. если у и х некоррелируемы.

Теперь формулу (1.9) можно переписать в следующем виде:

(1.11)

Подставив (1.11) в уравнение получим:

(1.12)

И, наконец, подставим (1.11) и (1.12) в уравнение линейной регрессии (2.2.1):

(1.13)

Уравнение (1.13) является выборочным уравнением регрессии.

1.2. Линейная множественная регрессия.

На практике при анализе результатов научных исследований часто имеет место ситуация, когда значение функции у зависит не от одной, а от нескольких переменных х. При проведении экспериментов в такой множественной ситуации исследователь записывает показания приборов о состоянии функции отклика (у) и всех факторов, от которых она зависит (хj). Результатами наблюдений являются уже не два вектор – столбца (у и х), как при проведении парного регрессионного анализа, а матрица результатов наблюдений:

(2.1)

где n — количество опытов;

p — число факторов;

хij — значение j — ого фактора для i — ого опыта;

уi — значение функции отклика для i — ого опыта.

Задача множественного регрессионного анализа состоит в построении такого уравнения плоскости в (р+1)- мерном пространстве, отклонения результатов наблюдений yi, от которой были бы минимальными. Или, другими словами, следует вычислить значения коэффициентов а0. аj в линейном полиноме:

(2.2)

что равносильно минимизации выражения (в дальнейшем индексы при знаке опущены):

(2.3)

где — вычисляемые значения исследуемой характеристики.

Для отыскания минимума выражения (2.3) необходимо найти частные производные по всем неизвестным а0, а1. аj. ар и приравнять их нулю.

Полученные уравнения образуют систему нормальных уравнений или в матричной форме:

где В — вектор столбец искомых коэффициентов аппроксимирующего полинома (2.2.2):

(2.5)

Х — матрица всех значений рассматриваемых факторов, полученных при проведении измерений или наблюдений:

(2.6)

хi0- вектор – столбец, определяющий свободный член уравнения регрессии. В матрице исходных данных этот столбец состоит из единиц; У — вектор – столбец опытных значений изучаемой характеристики:

(2.7)

Х*- матрица, транспонированная к матрице Х.

Для решения системы нормальных уравнений в матричной форме (2.2.4) следует умножить её слева на матрицу, обратную матрице системы нормальных уравнений, если таковая существует:

где Е — единичная матрица.

Таким образом, решение системы нормальных уравнений в матричной форме запишется следующим образом:

Каждый коэффициент уравнения регрессии можно найти по формуле:

аj= (2.11)

где сij – элементы обратной матрицы (Х*Х)-1.

В результате проведения всех этих операций получаем полином первой степени (2.2) с известными коэффициентами а0. аj,. Этот полином является аппроксимацией функции у=f(x1,x2,x3. xj,…,xp), вид которой неизвестен. Целесообразно напомнить ещё раз, что обычным методом наименьших квадратов можно построить только линейные по параметрам модели(парные и множественные).

Во множественном корреляционном анализе расчёты обычно начинают с вычисления парных коэффициентов корреляции, характеризующих тесноту связи между двумя величинами. В множественной ситуации вычисляют два типа парных коэффициентов корреляции:

1) ryxj — коэффициенты, определяющие тесноту связи между функцией отклика у и одним из факторов хj.

2) rxjxm — коэффициенты, показывающие тесноту связи между одним из факторов xj и фактором xm (j, m=1…p).

Формула для вычисления ryxj отличается от формулы (2.10), предназначенной для вычисления коэффициента парной корреляции, только индексом при х

(2.12)

Аналогично записывается формула и для вычисления коэффициента rxjxm.

Если один из коэффициентов rxjxm окажется равным 1, то это означает, что факторы xj и xm функционально связаны между собой и тогда целесообразно один из них исключить из рассмотрения, причём оставляют тот фактор, у которого коэффициент rxjxm больше.

После вычисления всех парных коэффициентов корреляции и исключения из рассмотрения того или иного фактора можно построить матрицу коэффициентов корреляции вида, где на главной диагонали стоят единицы.

Используя эту матрицу, можно вычислить частные коэффициенты корреляции, которые показывают степень влияния одного из факторов xj на функцию отклика у при условии, что остальные факторы закреплены на постоянном уровне.

Формула для вычисления частных коэффициентов корреляции такова:

(2.13)

где D1j — определитель матрицы, образованной из матрицы вычёркиванием 1-ой строки j-ого столбца. Определители D11 и Djj вычисляют аналогично. Как и парные коэффициенты, частные коэффициенты корреляции изменяются от -1 до 1.

Для изучения тесноты связи между функцией отклика у и несколькими факторами используют коэффициент множественной корреляции R.

Коэффициент множественной корреляции служит, как указывалось выше, и для оценки качества предсказания; R всегда положителен и изменяется от 0 до 1. Чем больше R, тем лучше качество предсказаний данной моделью опытных данных. Для вычисления коэффициента множественной корреляции используют матрицу:

(2.14)

Рассмотрение парного регрессионного анализа было начато с графической интерпретации, что удобно для понимания сущности метода наименьших квадратов). При изучении множественного регрессионного анализа такая возможность существует лишь когда число факторов = 2. Уравнение имеет вид:

(2.15)

Тогда для геометрической иллюстрации этой зависимости необходима трёхмерная диаграмма с отдельными осями для у, х1,х2.

Рис.1- Диаграмма модели с двумя независимыми переменными.

Основание диаграммы содержит оси для х1, х2. Наклонная плоскость над ним показывает величину у, соответствующую любому сочетанию х1и х2, измеренную расстоянием по вертикали от данной точки до этой плоскости. Но так как мы имеем статистическую зависимость, то фактические значения у будут лежать несколько выше или несколько ниже значений, соответствующих наклонной плоскости. Следовательно, теперь мы имеем трёхмерный аналог для двухмерной задачи, но вместо нахождения линии, соответствующей двухмерному рассеянию точек, мы теперь должны расположить плоскость так, чтобы она соответствовала трёхмерному рассеянию.

Проанализируем расположение плоскости на диаграмме модели (рис. 1). Если бы обе величины х1и х2 оказались равными нулю, то величина у равнялась бы а0 . При сохранении х1=0 уравнение (2.15) означает, что для любого положительного значения х2 величина у будет равна а0+а2х2. При сохранении х2=0, для любого отрицательного значения х1 величина у будет равна а0+а1х1.

2. Примеры исследования элементов эконометрического анализа для построения регрессионных моделей.

2.1. Построение линейной парной регрессионной модели.

Уравнение регрессии. Уравнение множественной регрессии

Во время учебы студенты очень часто сталкиваются с разнообразными уравнениями. Одно из них – уравнение регрессии — рассмотрено в данной статье. Такой тип уравнения применяется специально для описания характеристики связи между математическими параметрами. Данный вид равенств используют в статистике и эконометрике.

Определение понятия регрессии

В математике под регрессией подразумевается некая величина, описывающая зависимость среднего значения совокупности данных от значений другой величины. Уравнение регрессии показывает в качестве функции определенного признака среднее значение другого признака. Функция регрессии имеет вид простого уравнения у = х, в котором у выступает зависимой переменной, а х – независимой (признак-фактор). Фактически регрессия выражаться как у = f (x).

Какие бывают типы связей между переменными

В общем, выделяется два противоположных типа взаимосвязи: корреляционная и регрессионная.

Первая характеризуется равноправностью условных переменных. В данном случае достоверно не известно, какая переменная зависит от другой.

Если же между переменными не наблюдается равноправности и в условиях сказано, какая переменная объясняющая, а какая – зависимая, то можно говорить о наличии связи второго типа. Для того чтобы построить уравнение линейной регрессии, необходимо будет выяснить, какой тип связи наблюдается.

Виды регрессий

На сегодняшний день выделяют 7 разнообразных видов регрессии: гиперболическая, линейная, множественная, нелинейная, парная, обратная, логарифмически линейная.

Гиперболическая, линейная и логарифмическая

Уравнение линейной регрессии применяют в статистике для четкого объяснения параметров уравнения. Оно выглядит как у = с+т*х+Е. Гиперболическое уравнение имеет вид правильной гиперболы у = с + т / х + Е. Логарифмически линейное уравнение выражает взаимосвязь с помощью логарифмической функции: In у = In с + т* In x + In E.

Множественная и нелинейная

Два более сложных вида регрессии – это множественная и нелинейная. Уравнение множественной регрессии выражается функцией у = f(х₁ , х₂ . х_с)+E. В данной ситуации у выступает зависимой переменной, а х – объясняющей. Переменная Е — стохастическая, она включает влияние других факторов в уравнении. Нелинейное уравнение регрессии немного противоречиво. С одной стороны, относительно учтенных показателей оно не линейное, а с другой стороны, в роли оценки показателей оно линейное.

Обратные и парные виды регрессий

Обратная – это такой вид функции, который необходимо преобразовать в линейный вид. В самых традиционных прикладных программах она имеет вид функции у = 1/с + т*х+Е. Парное уравнение регрессии демонстрирует взаимосвязь между данными в качестве функции у = f (x) + Е. Точно так же, как и в других уравнениях, у зависит от х, а Е — стохастический параметр.

Понятие корреляции

Это показатель, демонстрирующий существование взаимосвязи двух явлений или процессов. Сила взаимосвязи выражается в качестве коэффициента корреляции. Его значение колеблется в рамках интервала [-1;+1]. Отрицательный показатель говорит о наличии обратной связи, положительный – о прямой. Если коэффициент принимает значение, равное 0, то взаимосвязи нет. Чем ближе значение к 1 – тем сильнее связь между параметрами, чем ближе к 0 – тем слабее.

Методы

Корреляционные параметрические методы могут оценить тесноту взаимосвязи. Их используют на базе оценки распределения для изучения параметров, подчиняющихся закону нормального распределения.

Параметры уравнения линейной регрессии необходимы для идентификации вида зависимости, функции регрессионного уравнения и оценивания показателей избранной формулы взаимосвязи. В качестве метода идентификации связи используется поле корреляции. Для этого все существующие данные необходимо изобразить графически. В прямоугольной двухмерной системе координат необходимо нанести все известные данные. Так образуется поле корреляции. Значение описывающего фактора отмечаются вдоль оси абсцисс, в то время как значения зависимого – вдоль оси ординат. Если между параметрами есть функциональная зависимость, они выстраиваются в форме линии.

В случае если коэффициент корреляции таких данных будет менее 30 %, можно говорить о практически полном отсутствии связи. Если он находится между 30 % и 70 %, то это говорит о наличии связей средней тесноты. 100 % показатель – свидетельство функциональной связи.

Нелинейное уравнение регрессии так же, как и линейное, необходимо дополнять индексом корреляции (R).

Корреляция для множественной регрессии

Коэффициент детерминации является показателем квадрата множественной корреляции. Он говорит о тесноте взаимосвязи представленного комплекса показателей с исследуемым признаком. Он также может говорить о характере влияния параметров на результат. Уравнение множественной регрессии оценивают с помощью этого показателя.

Для того чтобы вычислить показатель множественной корреляции, необходимо рассчитать его индекс.

Метод наименьших квадратов

Данный метод является способом оценивания факторов регрессии. Его суть заключается в минимизировании суммы отклонений в квадрате, полученных вследствие зависимости фактора от функции.

Парное линейное уравнение регрессии можно оценить с помощью такого метода. Этот тип уравнений используют в случае обнаружения между показателями парной линейной зависимости.

Параметры уравнений

Каждый параметр функции линейной регрессии несет определенный смысл. Парное линейное уравнение регрессии содержит два параметра: с и т. Параметр т демонстрирует среднее изменение конечного показателя функции у, при условии уменьшения (увеличения) переменной х на одну условную единицу. Если переменная х – нулевая, то функция равняется параметру с. Если же переменная х не нулевая, то фактор с не несет в себе экономический смысл. Единственное влияние на функцию оказывает знак перед фактором с. Если там минус, то можно сказать о замедленном изменении результата по сравнению с фактором. Если там плюс, то это свидетельствует об ускоренном изменении результата.

Каждый параметр, изменяющий значение уравнения регрессии, можно выразить через уравнение. Например, фактор с имеет вид с = y – тх.

Сгруппированные данные

Бывают такие условия задачи, в которых вся информация группируется по признаку x, но при этом для определенной группы указываются соответствующие средние значения зависимого показателя. В таком случае средние значения характеризуют, каким образом изменяется показатель, зависящий от х. Таким образом, сгруппированная информация помогает найти уравнение регрессии. Ее используют в качестве анализа взаимосвязей. Однако у такого метода есть свои недостатки. К сожалению, средние показатели достаточно часто подвергаются внешним колебаниям. Данные колебания не являются отображением закономерности взаимосвязи, они всего лишь маскируют ее «шум». Средние показатели демонстрируют закономерности взаимосвязи намного хуже, чем уравнение линейной регрессии. Однако их можно применять в виде базы для поиска уравнения. Перемножая численность отдельной совокупности на соответствующую среднюю можно получить сумму у в пределах группы. Далее необходимо подбить все полученные суммы и найти конечный показатель у. Чуть сложнее производить расчеты с показателем суммы ху. В том случае если интервалы малы, можно условно взять показатель х для всех единиц (в пределах группы) одинаковым. Следует перемножить его с суммой у, чтобы узнать сумму произведений x на у. Далее все суммы подбиваются вместе и получается общая сумма ху.

Множественное парное уравнение регрессии: оценка важности связи

Как рассматривалось ранее, множественная регрессия имеет функцию вида у = f (x₁,x₂,…,x_m)+E. Чаще всего такое уравнение используют для решения проблемы спроса и предложения на товар, процентного дохода по выкупленным акциям, изучения причин и вида функции издержек производства. Ее также активно применяют в самых разнообразным макроэкономических исследованиях и расчетах, а вот на уровне микроэкономики такое уравнение применяют немного реже.

Основной задачей множественной регрессии является построение модели данных, содержащих огромное количество информации, для того чтобы в дальнейшем определить, какое влияние имеет каждый из факторов по отдельности и в их общей совокупности на показатель, который необходимо смоделировать, и его коэффициенты. Уравнение регрессии может принимать самые разнообразные значения. При этом для оценки взаимосвязи обычно используется два типа функций: линейная и нелинейная.

Линейная функция изображается в форме такой взаимосвязи: у = а₀ + a₁х₁ + а₂х₂,+ . + a_mx_m. При этом _а2, a_m, считаются коэффициентами «чистой» регрессии. Они необходимы для характеристики среднего изменения параметра у с изменением (уменьшением или увеличением) каждого соответствующего параметра х на одну единицу, с условием стабильного значения других показателей.

Нелинейные уравнения имеют, к примеру, вид степенной функции у=ах₁ b1 х₂ b2 . x_m bm . В данном случае показатели b₁, b₂. b_m – называются коэффициентами эластичности, они демонстрируют, каким образом изменится результат (на сколько %) при увеличении (уменьшении) соответствующего показателя х на 1 % и при стабильном показателе остальных факторов.

Какие факторы необходимо учитывать при построении множественной регрессии

Для того чтобы правильно построить множественную регрессию, необходимо выяснить, на какие именно факторы следует обратить особое внимание.

Необходимо иметь определенное понимание природы взаимосвязей между экономическими факторами и моделируемым. Факторы, которые необходимо будет включать, обязаны отвечать следующим признакам:

• Должны быть подвластны количественному измерению. Для того чтобы использовать фактор, описывающий качество предмета, в любом случае следует придать ему количественную форму.
• Не должна присутствовать интеркорреляция факторов, или функциональная взаимосвязь. Такие действия чаще всего приводят к необратимым последствиям – система обыкновенных уравнений становится не обусловленной, а это влечет за собой ее ненадежность и нечеткость оценок.
• В случае существования огромного показателя корреляции не существует способа для выяснения изолированного влияния факторов на окончательный результат показателя, следовательно, коэффициенты становятся неинтерпретируемыми.

Методы построения

Существует огромное количество методов и способов, объясняющих, каким образом можно выбрать факторы для уравнения. Однако все эти методы строятся на отборе коэффициентов с помощью показателя корреляции. Среди них выделяют:

• Способ исключения.
• Способ включения.
• Пошаговый анализ регрессии.

Первый метод подразумевает отсев всех коэффициентов из совокупного набора. Второй метод включает введение множества дополнительных факторов. Ну а третий – отсев факторов, которые были ранее применены для уравнения. Каждый из этих методов имеет право на существование. У них есть свои плюсы и минусы, но они все по-своему могут решить вопрос отсева ненужных показателей. Как правило, результаты, полученные каждым отдельным методом, достаточно близки.

Методы многомерного анализа

Такие способы определения факторов базируются на рассмотрении отдельных сочетаний взаимосвязанных признаков. Они включают в себя дискриминантный анализ, распознание обликов, способ главных компонент и анализ кластеров. Кроме того, существует также факторный анализ, однако он появился вследствие развития способа компонент. Все они применяются в определенных обстоятельствах, при наличии определенных условий и факторов.