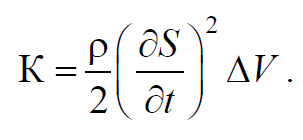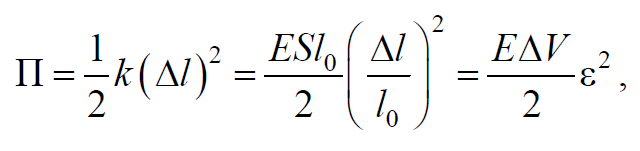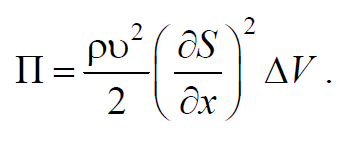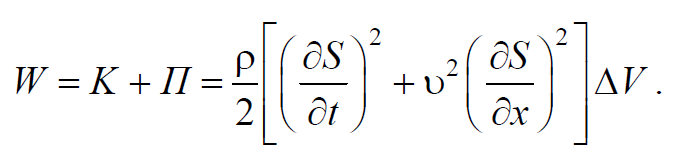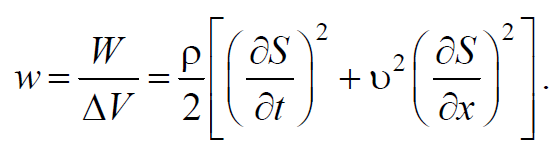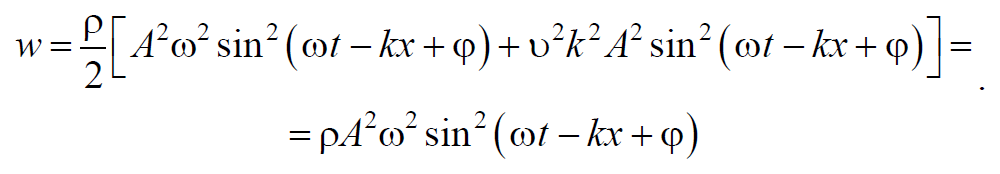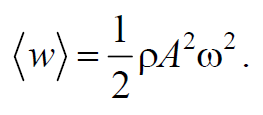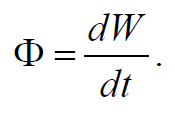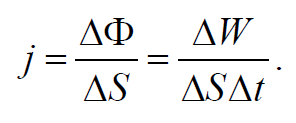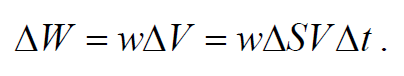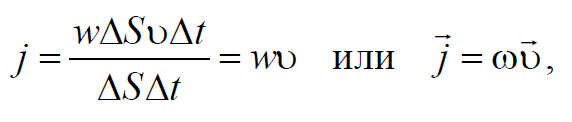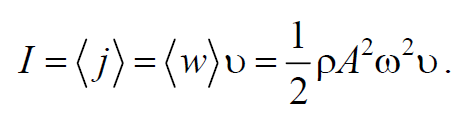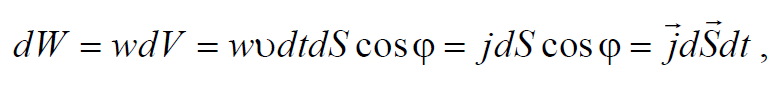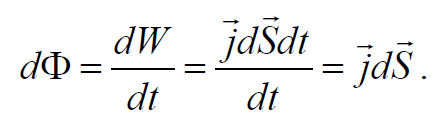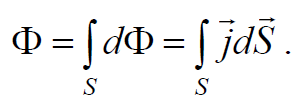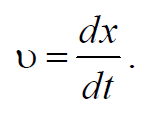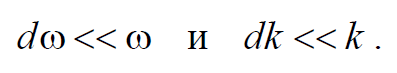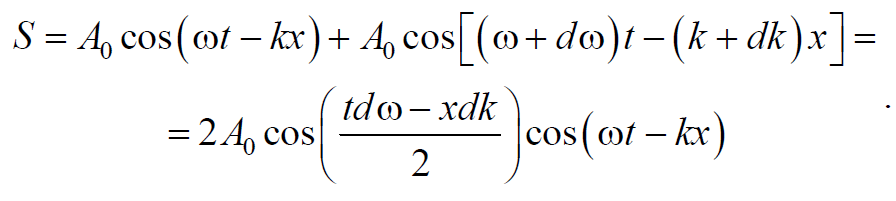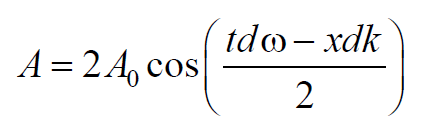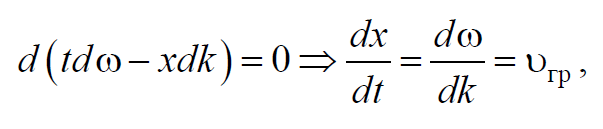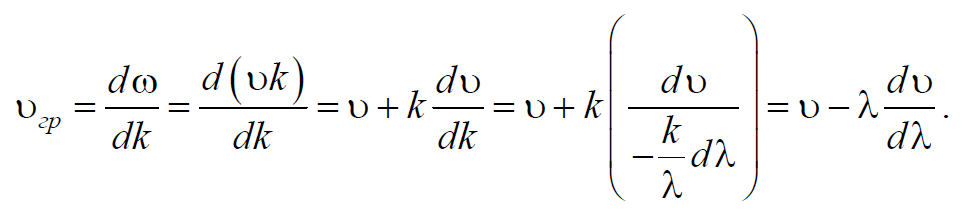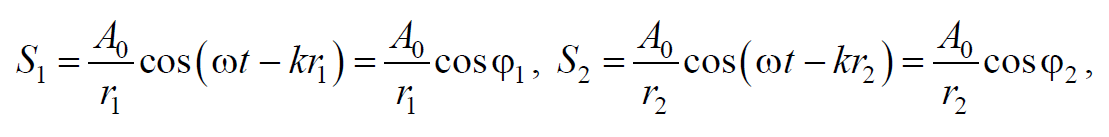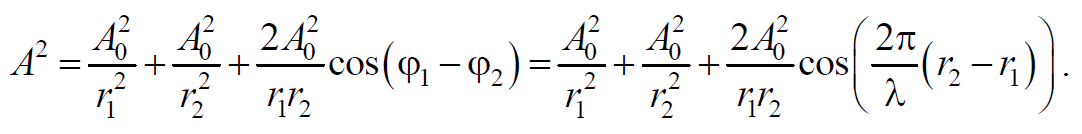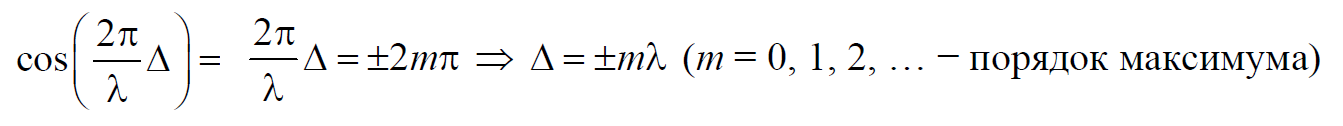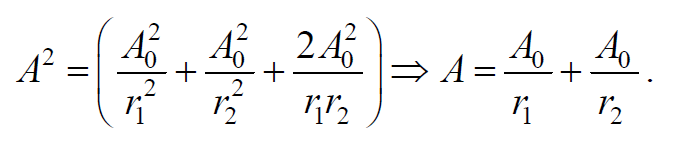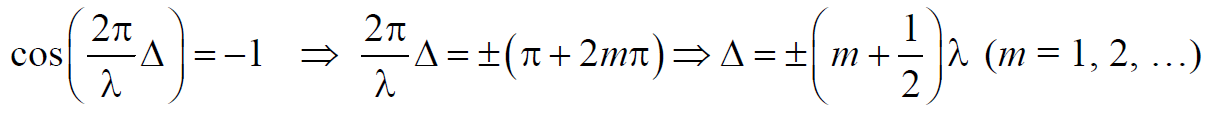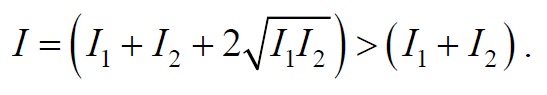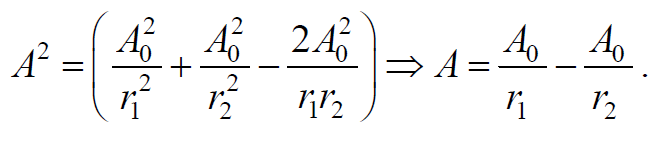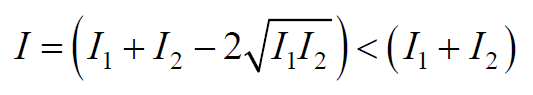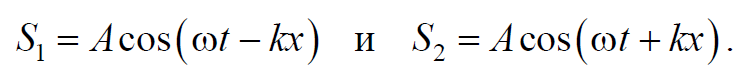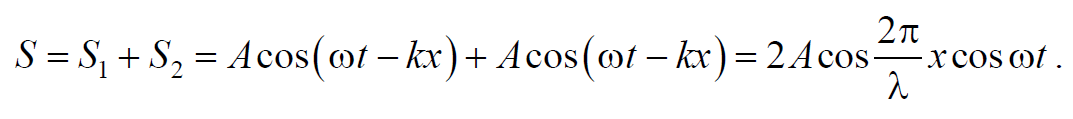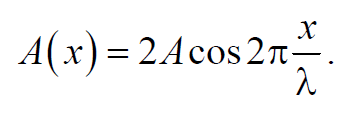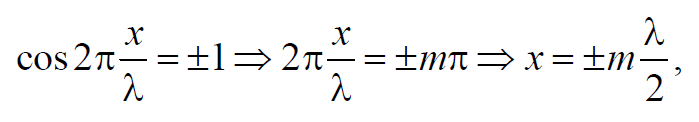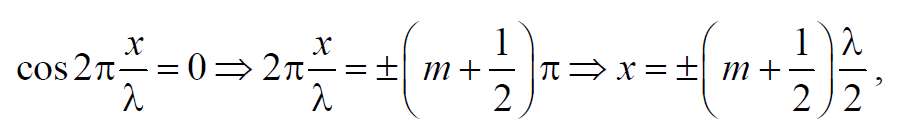Связь групповой и фазовой скорости.
Лекция 5: Механические волны
План:
1. Длина волны и волновое число.
2. Вывод уравнения плоской бегущей волны.
3. Уравнение плоской бегущей волны в комплексном виде.
4. Разность фаз колебаний.
6. Фазовая и скорость.
7. Групповая скорость.
8. Связь фазовой и групповой скорости.
9. Нахождение групповой скорости методом Эренфеста.
10. Уравнение сферической волны.
11. Вывод уравнения стоячей волны.
12. Координаты узлов и пучностей.
13. Энергия волн.
Длина волны и волновое число
Длиной волны 
Формулы длины волны легко получить из аналогии по формуле пути:




то 
Если из (2) выразить период и приравнять его к (3), получим:


Или 
Физический смысл отношения 




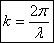

Вывод уравнения плоской бегущей волны
Бегущие волны – волны, которые переносят в пространстве энергию.
Плоские волны – волны, волновые поверхности которых – есть совокупность параллельных плоскостей, перпендикулярных направлению распространения волны.
Лучи в этом случае – параллельные прямые, совпадающие с направлением скорости распространения волны.
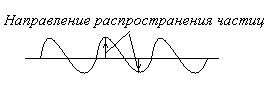
Пусть плоская бегущая волна распространяется вдоль оси X, т.е. вдоль одного направления из точки А в точку В как показано на рисунке:


Запишем уравнение колебания:

Рассмотрим распространение волны от точки М до точки В. Из рисунка видно, что время 


Перейдем от уравнения колебаний к уравнению плоской бегущей волны:
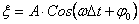
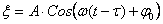
Т.к. за время 




Будем считать начальную фазу 
Тогда согласно уравнению (6), получаем: 
Если в уравнении (14) 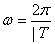


 | — первый вид уравненияплоской бегущей волны |
 | — второй вид уравненияплоской бегущей волны |
 | — третий вид уравненияплоской бегущей волны |
 | — четвертый вид уравненияплоской бегущей волны |

Уравнение плоской бегущей волны в комплексном виде.
Уравнение плоской бегущей волны 

Если 

Т.к. физический смысл имеет только реальная часть, получаем:

Получаем уравнение плоской бегущей волны комплексном виде:

 | — уравнения плоскойбегущей волны в комплексном виде |
Разность фаз колебаний
Фаза рассчитывается из определения углового перемещения:

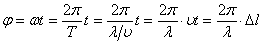

Виды волн
Основное свойство всех волн – перенос частицами среды энергии без переноса вещества.
Различают продольные и поперечные волны.
Волны, в которых частицы среды колеблются вдоль их распространения, называются продольными.
Волны, в которых частицы среды колеблются в плоскостях, перпендикулярных к направлению распространения волны, называются поперечными.
Продольные волны распространяются в жидкостях и газах
В твердой среде возникают как продольные, так и поперечные
Фазовая скорость
Пусть в волновом процессе фаза = const, т.е.


После дифференцирования, получим:

или 
Вывод: скорость распространения волны есть скорость перемещения фазы волны, поэтому ее называют фазовой скоростью и обозначают: 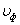



| Дисперсией называется зависимость фазовой скорости в среде от частоты распространение волн (дисперсия всегда связана с поглощением энергии средой) |
Групповая скорость
Рассмотрим простейшую группу волн, которая получается при наложении двух плоских волн с одинаковыми амплитудами и близкими частотами 


Это волна отличается от гармонической тем, что ее амплитуда есть медленно изменяющаяся функция координаты от времени, т.е. является негармонической.

 | — амплитуда группы волн |
Групповая скорость– скорость распространения группы волн,
Групповая скорость– скорость максимума огибающей группы волн или скорость движения центра волнового пакета.
Из условия 
получим: 

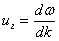 | — групповая скорость |
Связь групповой и фазовой скорости.
Групповая скорость определяется выражением:
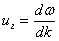
Определим отдельно выражения для 

1) 
Из выражения 
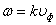
Продифференцируем это выражение по k: 
2) 
Выражения 

или 
Подставим выражения (34) и (35) в выражение для групповой скорости (32), получим:
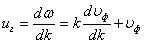


 | — связь фазовой и групповой скорости |
Из (38) следует, что 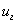
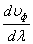
Если в среде не наблюдается дисперсия волн, то 
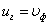
Понятие групповой скорости очень значимо, т.к. именно она фигурирует при измерении дальности радиолокации, в управлении космическими объектами.
Но 
9. Нахождение групповой скорости методом Эренфеста


Для этого нужно провести касательную к точке с координатами 

Лекция №10. Механические волны
6.5. Волновой перенос энергии и его характеристики: поток, плотность потока, интенсивность
Пусть в некоторой среде распространяется в направлении оси 0х плоская продольная волна $$S=Acos(ωt-kx+φ)$$ . Выделим в среде элементарный объем ΔV , настолько малый, чтобы скорость движения и деформацию во всех точках этого объема можно было считать одинаковыми и равными. Выделенный объем обладает кинетической энергией $$K=<1 \over 2>mv^2$$ . Если масса $$m=ρΔV$$ , а $$v=<∂S \over ∂t>$$ , то
Потенциальная энергия упругой деформации рассматриваемого объема
где $$k=
Тогда полная энергия упругой волны
Определим плотность энергии, разделив (6.5.4) на объем ΔV
Продифференцируем уравнение плоской продольной волны (6.2.8) по времени t и по координате х и подставим выражения в формулу (6.5.5) учтя, что $$k^2υ^2=ω^2$$
Среднее значение квадрата синуса равно 1/2. Соответственно среднее по времени значение плотности энергии в каждой точке среды равно
Таким образом, плотность энергии и среднее значение плотности энергии пропорциональны плотности среды ρ , квадрату частоты ω и квадрату амплитуды волны А .
Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии через эту поверхность. Поток энергии Ф через данную поверхность равен энергии dW переносимой за время dt
Ф измеряется в ваттах.
Для характеристики распространения энергии в разных точках пространства вводится векторная величина, называема плотностью потока энергии. Плотность потока энергии численно равна потоку энергии через единичную площадку ΔS , помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.
Если через площадку ΔS , перпендикулярную к направлению распространения волны, переносится энергия ΔW за время Δt , то плотность потока энергии равна
Рассмотрим объем цилиндра с основанием ΔS и высотой υΔt ( υ − фазовая скорость волны). В случае малого объема цилиндра, плотность энергии во всех точках цилиндра можно было считать одинаковой и поэтому энергию можно найти как произведение плотности энергии ω на объем ΔV=ΔSυΔt
Подставив выражение (6.5.10) в последнее выражение, получим
где j − вектор плотности потока энергии, называемый вектором Умова.
Интенсивность волны равна
Данное выражение справедливо для волны любого вида.
Определим поток энергии через поверхность S . Для этого разобьем поверхность на элементарные участки dS . За время dt через площадку dS пройдет энергия dW . Объем цилиндра, где вычисляется энергия, равен $$dV = υdtdScosϕ$$ . Тогда в этом объеме содержится энергия
где d S = n dS ; n − единичный вектор нормали к поверхности dS .
Поток энергии через элементарную поверхность dS
Поток энергии через поверхность S равен
6.6. Фазовая и групповая скорости волн
Скорость распространения волны есть скорость перемещения фазы и называется фазовой скоростью. Фазовая скорость равна
Если в среде распространяется одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности, и к ним применим принцип суперпозиции волн: при распространении в линейной среде (т. е. среде снеизменяющимися свойствами) нескольких волн, каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов.
Используя принципа суперпозиции, любая волна может быть представлена в виде волнового пакета. Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства. Простейший волновой пакет двух распространяющихся вдоль положительного направления оси Х гармонических волн с одинаковыми амплитудами, близкими частотами и волновыми числами, причем
Эта волна отличается от гармонической тем, что ее амплитуда
медленно изменяющаяся функция координаты х и времени t .
За скорость распространения волнового пакета принимают скорость перемещения максимума амплитуды волны. При условии, что $$tdω-xdk=const$$ , получим
где υгр – групповая скорость. Рассмотрим связь между групповой и фазовой скоростями. Учитывая, что волновое число $$k=<2π \over λ>$$ и $$dk=-<2π \over λ^2>dλ=-
В теории относительности доказывается, что групповая скорость υгр ≤ c , в то время как для фазовой скорости ограничений не существует.
6.7. Интерференция упругих волн
Для того чтобы рассмотреть интерференцию волн, введем понятие когерентности . Согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов связано с понятием когерентности. Волны называются когерентными , если разность их фаз остается постоянной во времени. При наложении в пространстве двух или нескольких когерентных волн в разных его точках получается усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн. Это явление называется интерференцией волн, и заключается в том, что колебания в одних точках усиливают, а в других ослабляют друг друга.
Рассмотрим наложение двух когерентных сферических волн, возбуждаемых точечными источниками $$S_1$$ и $$S_2$$ , колеблющимися с одинаковыми амплитудой, частотой, нулевой начальной фазой и постоянной разностью фаз. Запишем уравнения колебаний:
где $$r_1$$ и $$r_2$$ − расстояния от источников волн до рассматриваемой точки.
Амплитуда результирующей волны равна (сложение одинаково направленных колебаний)
Так как разность начальных фаз $$(ϕ_1-ϕ_2)=<2π \over λ>(r_2-r_1)=<2π \over λ>Δ=const$$ , то результат наложения двух волн в различных точках зависит от величины $$Δ=r_2-r_1$$ , называемой разностью хода волн.
В точках, где выполняется условие
Так как квадрат амплитуды колебаний пропорционален интенсивности волны, то получаем
То есть наблюдается усиление интенсивности (увеличение амплитуду) результирующей волны или интерференционный максимум.
2) В точках, где выполняется условие
То есть наблюдается ослабление интенсивности (уменьшение амплитуды) результирующей волны или интерференционный минимум.
Таким образом, в результате наложения двух когерентных волн в среде возникают колебания, амплитуда которых различна в разных точках среды, при этом в каждой точке среды получается или максимум амплитуды, или минимум амплитуды, или ее промежуточное значение − в зависимости от значения разности расстояний точки до когерентных источников. Интерференция света приводит к перераспределению энергии волны между соседними областями, хотя в среднем для больших областей энергия остается неизменной.
6.8. Стоячие волны
Рассмотрим интерференцию стоячих волн. Стоячие волны − это волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.
Запишем уравнение двух плоских волн, распространяющихся вдоль оси Х в противоположных направлениях
Сложив вместе эти уравнения и преобразовав результат по формуле для суммы косинусов, получим уравнение стоячей волны
Из данного уравнения видно, что в каждой точке стоячей волны происходят колебания той же частоты, что и у встречных волн, причем амплитуда зависит от координаты х
Точки, в которых амплитуда колебаний достигает максимального значения и координаты которых удовлетворяют условию
где m = 0, 1, 2, … называются пучностями стоячей волны.
Точки, в которых амплитуда колебаний обращается в нуль и координаты которых удовлетворяют условию
где m = 0, 1, 2, … называются узлами стоячей волны.
Волновой пакет. Фазовая и групповая скорость электромагнитной волны
Всякая реальная электромагнитная волна представляет собой суперпозицию (наложение) волн, частоты которых заключены в некотором интервале Dw. Суперпозиция волн, мало отличающихся по частоте (или длине волн), называется волновым пакетом (или группой волн). Уравнение группы волн имеет вид:
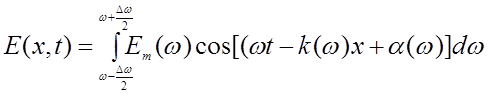
 |
Волны, образующие пакет, отличаются друг от друга по l, а, следовательно, и по 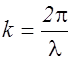
В том месте, где в данный момент волны больше всего усиливают друг друга, будет наблюдаться максимум. С течением времени максимум будет перемещаться с некоторой скоростью 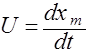
Будем считать, что Dw
Дата добавления: 2015-07-22 ; просмотров: 2837 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://physics.belstu.by/mechanics_lk/mechanics_lk10.html
http://helpiks.org/4-19747.html