Виды фазовых портретов для линейных систем второго порядка
| Корни характеристического уравнения | Переходный процесс | Фазовая траектория |
1. a1=0, a2>0  |  | 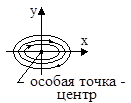 |
2. a1 2 >4a2, a1>0, a2>0  |  | 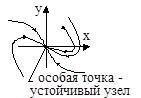 |
3. a2 2 0 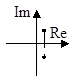 | 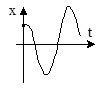 | 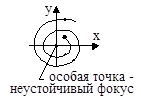 |
5. a1 2 0, a2>0 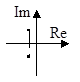 |  | 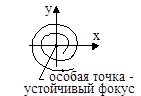 |
6. a1 2 >4a2, a1 0  | 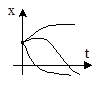 | 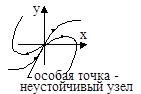 |
Вид и расположение фазовых траекторий, а также направление движения по ним изображающей точки дают возможность судить о характере движения системы и его устойчивости при различных начальных отклонениях. Особые точки и их характер определяют состояние равновесия исходной системы.
Реальные автоматические системы можно считать линейными в предположении малости отклонений переменных от их установившихся значений. За пределами указанной области картина фазовых траекторий может стать качественно иной. В частности, если по линейной теории система неустойчивая и процесс расходится, то может оказаться, что из-за фактической нелинейности характеристик он не будет расходящимся неограниченно. Картина фазовых траекторий для такой системы изображена на рис. 2.15,а. Здесь вблизи начала координат получаются спирали, как в неустойчивой линейной системе, но далее они приближаются асимптотически к замкнутому контуру ограниченных размеров. К нему же приближаются и все спирали, находящиеся вне контура. Такого рода замкнутый контур представляет собой особый вид линий на фазовой плоскости и называется устойчивым предельным циклом. Устойчивый предельный цикл соответствует автоколебаниям системы. Размеры предельного цикла представляют амплитуды колебаний самой величины x и скорости ее изменения y. Для определения периода автоколебаний необходимо решить уравнение системы во времени.
Рис. 2.15. Фазовые траектории нелинейных систем:
а — устойчивый предельный цикл; б — неустойчивый предельный цикл;
в — фазовый портрет системы с сепаратрисами
Замкнутые фазовые траектории на фазовой плоскости называются предельными циклами, которые могут быть как устойчивыми (рис. 2.15,а), так и неустойчивыми (рис. 2.15,б). К этим предельным циклам стремятся изображающие точки при различных начальных отклонениях по различным фазовым траекториям.
В различных частях фазовой плоскости фазовые траектории нелинейной системы могут быть различными (рис. 2.15,в). Линии, разделяющие фазовую плоскость на участки с различными фазовыми траекториями, называются сепаратрисами. Поведение системы в каждой области фазовой плоскости описывается своим дифференциальным уравнением.
Кроме того, для фазового портрета нелинейных систем с разрывными характеристиками характерно наличие линий переключения, которые также разделяют фазовую плоскость на ряд областей с различными фазовыми траекториями. При этом начальные значения переменных на каждом участке определяются через их конечные значения на предыдущем участке. Линии переключения характеризуются узловыми точками разрывных характеристик нелинейных элементов.
Замечание: координатами (x, y) фазовой плоскости могут служить не обязательно отклонение (ошибка) управляемой величины системы и ее скорость. Для этой цели могут быть взяты любые две переменные, однозначно характеризующие состояние системы второго порядка в произвольный момент времени.
Пример. Изобразим на фазовой плоскости переходный процесс и автоколебания в автоматической системе (рис. 2.1), линейная часть которой задана передаточной функцией
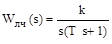
где k — коэффициент передачи;
T — постоянная времени,
а нелинейный элемент — статической характеристикой yн = F(x).
Р е ш е н и е. В качестве координат фазовой плоскости выбираем отклонение управляемой величины x и скорость ее изменения y = dx/dt. Запишем для ошибки x дифференциальное уравнение системы, описывающее ее свободное движение

которое заменяем эквивалентными уравнениями первого порядка
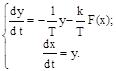
Разделив первое из уравнений (2.43) на второе, получаем дифференциальное уравнение фазовых траекторий

решение которого определяется характеристикой нелинейного элемента.
Рассмотрим фазовые портреты системы для некоторых типов нелинейных элементов.
1. Идеальное двухпозиционное реле (рис. 2.4,а) со статической характеристикой F(x) = csign(x).
Дифференциальное уравнение (2.44) фазовых траекторий в этом случае примет вид
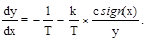
Переключение идеального реле происходит при x = 0. Следовательно, линия переключения на фазовой плоскости (рис. 2.16,а) совпадает с осью ординат.
Справа от линии переключения при x > 0 дифференциальное уравнение фазовых траекторий будет
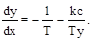
Его интегрирование дает уравнение фазовой траектории [2]
x = kcT ln½y + kc½ — Ty + c 0 , (2.47)
где c 0 — постоянная интегрирования, определяемая начальными условиями. Каждому конкретному c 0 соответствует определенная кривая на фазовой плоскости справа от линии переключения. Эти кривые имеют асимптоту y = -kc.
Слева от линии переключения при x 0 , (2.49)
согласно которому наносится семейство фазовых траекторий с асимптотой y = kc в левой фазовой полуплоскости.
На рис. 2.16,а изображены фазовые траектории системы для начальных условий (x0, 0).
Рис. 2.16. Фазовые траектории релейных систем:
а — с идеальным реле; б — с реле с гистерезисом
2. Двухпозиционное реле с гистерезисом (рис. 2.4,в) со статической характеристикой
Переключение реле с гистерезисом происходит при x = +b, если y > 0 (линия AB на рис. 2.16,б); если же y 0 к координатным осям, для которой xi = x0i, что соответствует отображению каждой точки полуоси 0X самой в себя, т.е. после обхода вокруг начала координат точка возвращается в исходное положение. Пересечение кривой xi = f(x0i) с прямой xi = x0i (точки A и B) определяют существование предельного цикла. Если указанная кривая и прямая не пересекаются, то автоколебания невозможны, а если касаются, то имеет место один предельный цикл.
Чтобы определить, какому типу предельного цикла это соответствует, надо взять на оси абсцисс начальную точку x0 сначала слева, а затем справа от точки пересечения и проследить ход точечного преобразования, как показано стрелками на рис. 2.19.
Рис. 2.19 соответствует двум предельным циклам, из которых меньший (точка A) неустойчив, а больший (точка B) устойчив. Следовательно, при начальных условиях (x0, y0), расположенных внутри меньшего предельного цикла, система устойчива, а при всяких других начальных условиях она стремится к установившемуся автоколебательному процессу.
ложение. Пересечение кривой xi = f(x0i) с прямой xi = x0i (точки A и B) определяют существование предельного цикла. Если указанная кривая и прямая не пересекаются, то автоколебания невозможны, а если касаются, то имеет место один предельный цикл.
Чтобы определить, какому типу предельного цикла это соответствует, надо взять на оси абсцисс начальную точку x0 сначала слева, а затем справа от точки пересечения и проследить ход точечного преобразования, как показано стрелками на рис. 2.19.
Рис. 2.19 соответствует двум предельным циклам, из которых меньший (точка A) неустойчив, а больший (точка B) устойчив. Следовательно, при начальных условиях (x0, y0), расположенных внутри меньшего предельного цикла, система устойчива, а при всяких других начальных условиях она стремится к установившемуся автоколебательному процессу.
Дата добавления: 2015-06-01 ; просмотров: 7375 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Фазовые портреты линейных систем второго порядка
Дата добавления: 2014-04-22 ; просмотров: 7087 ; Нарушение авторских прав
Для получения уравнений, описывающих фазовый портрет системы второго порядка, необходимо в системе дифференциальных уравнений (12.6) второе уравнение поделить на первое и исключить из рассмотрения время t, в результате чего получают:
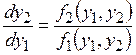
Решение этого уравнения дает семейство интегральных кривых на фазовой плоскости, по которым строят фазовые траектории системы.
Фазовые портреты линейных систем второго порядка классифицируют по типам особых точек.
Линейную систему второго порядка описывают уравнением
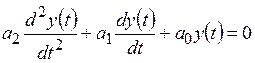
где y(t) − выходная координата системы; а0, а1, a2 − постоянные коэффициенты. Обозначив y(t) = y1(t), 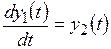

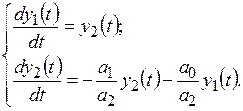
Разделив второе уравнение на первое, получают

решением которого будет уравнение фазовых траекторий
где сi − постоянные интегрирования.
Возможны шесть различных типов фазовых траекторий в зависимости от корней характеристического уравнения a2s 2 + a1s + a0 = 0.
Случай 1. Корни − мнимые при a1=0, a0>0, a2>0; s1,2=±iω; 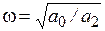
Система находится на границе устойчивости.
График y1(t) показан на рис. 13.1. Для получения уравнения фазовой траектории выражения (13.8) и (13.9) возводят в квадрат и складывают, в результате получают уравнение
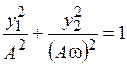
Незатухающим периодическим колебаниям в системе соответствует на фазовой плоскости замкнутая фазовая траектория. Особая точка системы является геометрическим центром фазовых траекторий и носит название центр, а сама система называется консервативной.
Рис. 13.1. Фазовый портрет типа центр: а) плоскость корней
характеристического уравнения; б) переходный процесс; в) фазовый портрет
Случай 2. Корни − комплексные и имеют отрицательные вещественные части при а1 0, a1 > 0, а2 > 0: s1,2 = −α ± iω (рис. 13.2а),
α = −a1/(2а2), 
Решение уравнения (13.4) имеет вид
где d = arctg(a/w); 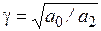
Рис. 13.2. Фазовый портрет типа устойчивый фокус: а) расположение корней
характеристического уравнения; б) переходный процесс; в) фазовый портрет
Уравнения (13.11) и (13.12) дают в фазовой плоскости параметрическое уравнение спиралей. С каждым оборотом, соответствующим одному периоду колебаний, изображающая точка приближается к началу координат, так как значения y1 и y2за период колебаний становятся меньше.
Особая точка называется устойчивым фокусом.
Случай 3.Корни − комплексные и имеют положительные вещественные части при а1 0, a1 0: s1,2 = α ± iω (рис. 13.3а), система неустойчива. Откуда
Рис. 13.3 Фазовый портрет типа неустойчивый фокус: а) расположение корней
характеристического уравнения; б) переходный процесс; в) фазовый портрет
Состоянию неустойчивого равновесия системы соответствует особая точка, которая называется неустойчивый фокус (рис. 13.3в). В системе возникает колебательный процесс с возрастающей амплитудой.
Случай 4. Корни – вещественные отрицательные при а1 > 4а0a2; a0 > 0, a1 > 0, а2 > 0: s1,2 = −α±b (рис. 13.4а), α = a1/(2а2), 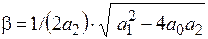
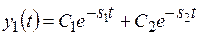
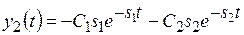
Границей областей с переходными процессами типа 1 и 2 служат прямые с уравнениями y2 = −s2y1 и y2 = −s1y1.
Все фазовые траектории вливаются в начало координат − особую точку, называемую устойчивым узлом (рис. 13.4). Время движения к состоянию равновесия теоретически равно бесконечности.
Рис. 13.4. Фазовый портрет типа устойчивый узел: а) расположение корней
характеристического уравнения; б) переходный процесс; в) фазовый портрет
Случай 5. Корни − вещественные положительные при а1>4а0a2; a0>0, a1 0: s1,2 = α ± b (рис. 13.5а), система неустойчива. Решение уравнения (13.4):


Рис. 13.5. Фазовый портрет типа неустойчивый узел: а) расположение корней
характеристического уравнения; б) переходный процесс; в) фазовый портрет
Фазовые траектории направлены от начала координат в бесконечность. Особая точка носит название неустойчивый узел (рис. 13.5). Крайние траектории определяются уравнениями y2 = s1y1 и y2 = s2y1.
Случай 6. Корни − вещественные и имеют различные знаки при a0 0, a2 > 0: s1 = −α1, s2 = β. В этом случае система неустойчива.
Частным является случай, когда a1=0, и, учитывая, что a0
Фазовая плоскость для уравнения 2 порядка
Система обыкновенных дифференциальных уравнений называется автономной, если независимая переменная не входит явно в систему.
В теории автономных систем принято обозначать независимую переменную буквой t, а искомое решение — 
Ограничимся случаем n = 2 и в дальнейшем рассматриваем автономные системы второго порядка: 
Будем полагать, что правые части системы f1(x1, x2 ) , f2(x1, x2) непрерывно дифференцируемы в области 
Пусть x1=j1(t), x2= j2(t) — решение автономной системы второго порядка. Тогда уравнения 
задают в параметрической форме кривую на плоскости. Эта кривая называется фазовой кривой или фазовой траекторией системы. Плоскость, на которой расположены фазовые траектории называется фазовой плоскостью автономной системы. Для n >2 фазовые траектории располагаются в фазовом пространстве.
Если на рисунке изображено несколько фазовых кривых системы, характеризующих качественное поведение решений системы (кривые с одинаковыми асимптотами, предельными точками и пр.), то такое изображение называется фазовым портретом системы.
Интегральные кривые рассматриваемой системы изображаются в трехмерном пространстве переменных (t, x1, x2) и, если x1= f 1(t), x2= f 2(t) — решение системы, то интегральная кривая задается в параметрической форме уравнениями 
а фазовая траектория — не что иное, как проекция интегральной кривой на фазовую плоскость (плоскость (x1, x2).
ПРИМЕР 1. Фазовые кривые автономной системы.
Для фазовых кривых (фазовых траекторий) автономной системы с непрерывно дифференцируемой правой частью 

справедливы следующие утверждения:
- Если существует такая точка
, что
, то
, является решением автономной системы, т.е. соответствующая фазовая траектория — точка.
- Если точка (x1(t), x2(t)) принадлежит некоторой фазовой кривой, то при любой постоянной С точка (x1(t+С), x2(t+С)) принадлежит той же фазовой кривой.
- Две фазовые кривые либо не имеют общих точек, либо совпадают.
- Фазовая траектория, отличная от точки, есть гладкая кривая (в каждой ее точке есть ненулевой касательный вектор).
- Всякая фазовая кривая принадлежит к одному из трех типов— гладкая кривая без самопересечений, замкнутая гладкая кривая (цикл), точка.
- Если фазовая кривая, отвечающая решению
, есть гладкая замкнутая кривая, то это решение — периодическая функция.
ПРИМЕР 2. Типы фазовых кривых.
Точка 

ПРИМЕР 3. Точки покоя автономной системы.
Если в каждой точке области 



в векторной форме: 
где 

Автономная система 
полностью определяется заданием векторного поля 
Действительно, в каждой точке 
гладкой фазовой кривой

существует касательный вектор
(x'(t0 ), y'(t0 ))
равный (в силу системы) вектору 
иными словами, векторное поле 
автономной системы задает в каждой точке направление касательной к фазовой кривой системы, проходящей через эту точку.
Точки векторного поля, в которых вектор 
ПРИМЕР 4. Векторное поле автономной системы.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
http://life-prog.ru/1_28796_fazovie-portreti-lineynih-sistem-vtorogo-poryadka.html
http://old.exponenta.ru/EDUCAT/CLASS/courses/ode/theme12/theory.asp


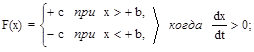
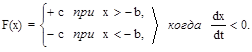





 , является решением автономной системы, т.е. соответствующая фазовая траектория — точка.
, является решением автономной системы, т.е. соответствующая фазовая траектория — точка. , есть гладкая замкнутая кривая, то это решение — периодическая функция.
, есть гладкая замкнутая кривая, то это решение — периодическая функция.