Фазовая скорость бегущей волны
Предположим, что при волновом процессе фаза постоянна, т.е.:

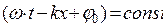
Продифференцировав выражение (22.9), и сократив на ω получим 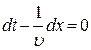
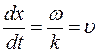
где υ – скорость распространения волны в уравнении (22.10) есть скорость перемещения фазы волны и называется фазовой скоростью.
Если фазовая скорость волн в среде зависит от их частоты, то это явление называют дисперсией волн.
Аналогичными рассуждениями выведем уравнение сферической волны – волны, волновые поверхности которой имеют вид концентрических сфер:
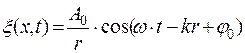
где r –расстояние от центра волны до рассматриваемой точки среды.
В случае сферической волны, даже в среде не поглощающей энергию амплитуда колебаний не остается постоянной, а изменятся по закону 1/r. Уравнение (22.11) справедливо лишь для r значительно превышающих размеры источника (тогда источник колебаний можно считать точечным).
Распространение волн в однородной изотропной среде в общем случае записывается волновым уравнением- дифференциальным уравнением в частных производных:
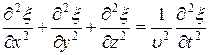
где υ – фазовая скорость,
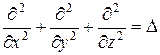
Тогда уравнение (22.12) можно записать
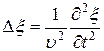
Решением уравнения (22.12) является уравнение любой волны (плоской или сферической). Соответствующей подстановкой моно убедиться что уравнению (22.13) удовлетворяют решения для плоской волны (22.8) или (22.11) для сферической волны. Для плоской волны, распространяющейся вдоль оси х, волновое уравнение принимает вид:
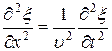
Дата добавления: 2016-01-29 ; просмотров: 678 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Связь групповой и фазовой скорости.
Лекция 5: Механические волны
План:
1. Длина волны и волновое число.
2. Вывод уравнения плоской бегущей волны.
3. Уравнение плоской бегущей волны в комплексном виде.
4. Разность фаз колебаний.
6. Фазовая и скорость.
7. Групповая скорость.
8. Связь фазовой и групповой скорости.
9. Нахождение групповой скорости методом Эренфеста.
10. Уравнение сферической волны.
11. Вывод уравнения стоячей волны.
12. Координаты узлов и пучностей.
13. Энергия волн.
Длина волны и волновое число
Длиной волны 
Формулы длины волны легко получить из аналогии по формуле пути:




то 
Если из (2) выразить период и приравнять его к (3), получим:


Или 
Физический смысл отношения 




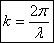

Вывод уравнения плоской бегущей волны
Бегущие волны – волны, которые переносят в пространстве энергию.
Плоские волны – волны, волновые поверхности которых – есть совокупность параллельных плоскостей, перпендикулярных направлению распространения волны.
Лучи в этом случае – параллельные прямые, совпадающие с направлением скорости распространения волны.
Пусть плоская бегущая волна распространяется вдоль оси X, т.е. вдоль одного направления из точки А в точку В как показано на рисунке:


Запишем уравнение колебания:

Рассмотрим распространение волны от точки М до точки В. Из рисунка видно, что время 


Перейдем от уравнения колебаний к уравнению плоской бегущей волны:
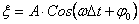
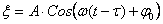
Т.к. за время 




Будем считать начальную фазу 
Тогда согласно уравнению (6), получаем: 
Если в уравнении (14) 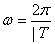


 | — первый вид уравненияплоской бегущей волны |
 | — второй вид уравненияплоской бегущей волны |
 | — третий вид уравненияплоской бегущей волны |
 | — четвертый вид уравненияплоской бегущей волны |

Уравнение плоской бегущей волны в комплексном виде.
Уравнение плоской бегущей волны 

Если 

Т.к. физический смысл имеет только реальная часть, получаем:

Получаем уравнение плоской бегущей волны комплексном виде:

 | — уравнения плоскойбегущей волны в комплексном виде |
Разность фаз колебаний
Фаза рассчитывается из определения углового перемещения:

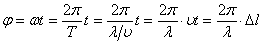

Виды волн
Основное свойство всех волн – перенос частицами среды энергии без переноса вещества.
Различают продольные и поперечные волны.
Волны, в которых частицы среды колеблются вдоль их распространения, называются продольными.
Волны, в которых частицы среды колеблются в плоскостях, перпендикулярных к направлению распространения волны, называются поперечными.
Продольные волны распространяются в жидкостях и газах
В твердой среде возникают как продольные, так и поперечные
Фазовая скорость
Пусть в волновом процессе фаза = const, т.е.


После дифференцирования, получим:

или 
Вывод: скорость распространения волны есть скорость перемещения фазы волны, поэтому ее называют фазовой скоростью и обозначают: 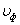



| Дисперсией называется зависимость фазовой скорости в среде от частоты распространение волн (дисперсия всегда связана с поглощением энергии средой) |
Групповая скорость
Рассмотрим простейшую группу волн, которая получается при наложении двух плоских волн с одинаковыми амплитудами и близкими частотами 


Это волна отличается от гармонической тем, что ее амплитуда есть медленно изменяющаяся функция координаты от времени, т.е. является негармонической.

 | — амплитуда группы волн |
Групповая скорость– скорость распространения группы волн,
Групповая скорость– скорость максимума огибающей группы волн или скорость движения центра волнового пакета.
Из условия 
получим: 

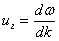 | — групповая скорость |
Связь групповой и фазовой скорости.
Групповая скорость определяется выражением:
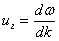
Определим отдельно выражения для 

1) 
Из выражения 
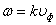
Продифференцируем это выражение по k: 
2) 
Выражения 

или 
Подставим выражения (34) и (35) в выражение для групповой скорости (32), получим:
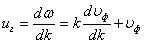


 | — связь фазовой и групповой скорости |
Из (38) следует, что 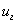
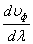
Если в среде не наблюдается дисперсия волн, то 
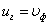
Понятие групповой скорости очень значимо, т.к. именно она фигурирует при измерении дальности радиолокации, в управлении космическими объектами.
Но 
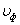
9. Нахождение групповой скорости методом Эренфеста


Для этого нужно провести касательную к точке с координатами 

Формула скорости волны
Фронт волны (волновая поверхность) — это геометрическое место точек среды, для которых в некоторый момент времени фаза волны имеет одно и то же значение.
Скоростью волны называют скорость, с которой движется фронт волны.
Формула фазовой скорости волны
Рассмотрим одномерный случай для гармонической волны. Уравнение волновой поверхности при это запишем как:
\[Ф_s=\omega t-kx+\varphi \ \left(1\right),\]
где$<\ Ф>_s$ — фаза волны; $k=\frac<2\pi ><\lambda >$ — волновое число; $\lambda $ — длина волны; $\omega $ — циклическая частота; $\varphi $ — начальная фаза. Уравнению (1) в каждый момент времени соответствует только одна точка оси X координата которой, равна:
Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне превращается в точку. Из формулы (2) видно, что волновые поверхности перемещаются в среде со скоростью:
где $T$ — период колебаний точек в волне.
Если волны гармонические, то скорость движения волновой поверхности равна скорости распространения волны. Скорость, которую определяет выражение (3) является фазовой скоростью.
Фазовая скорость гармонической волны совпадает со скорость распространения энергии волны.
Скорость волны зависит от вещества, в котором распространяется волна и типа волны. Скорость волны — это не то же самое, что скорость колебания частиц среды в волне.
Формула для вычисления фазовой скорости распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях может быть вычислена как:
где $K$ — модуль объемной упругости вещества; $\rho =const$ — плотность среды. В газах формула (4) выполняется, если избыточное давление много меньше, равновесного давление газа в невозмущенном состоянии.
Для нахождения скорости распространения продольных волн в газе применяют выражение:
где $\gamma $ — показатель адиабаты; $p$ — давление газа.
Продольные механические волны могут распространяться в твердых телах, их фазовая скорость равна:
где $E$ — модуль Юнга вещества стержня.
Формула для фазовой скорости распространения поперечных волн
Поперечные механические волны способны распространяться только в твердых телах. Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде при этом можно найти как:
где $G$ — модуль сдвига среды; $\rho $ — плотность вещества.
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
Формула для групповой скорости волн
Кроме фазовой скорости для описания распространения диспергирующих волн применяют понятие групповой скорости. При этом фазовая скорость может зависеть от частоты, при этом в веществе распространяются волны сложного негармонического характера, тогда с групповую скорость проще использовать, как характеристику скорости распространения волн.
Групповой скоростью называют скорость перемещения группы (цуга) волн, которые создают в каждый момент времени, локализованный в пространстве, волновой пакет. Любая реальная волна представляет собой суперпозицию гармонических волн. Скорость, с которой такая волна распространяется в веществе, имеющем дисперсию, равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.
Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой:
Если дисперсия отсутствует, то $\frac
Примеры задач с решением
Задание. За время равное $t=20$ c волне совершается $N=$100 колебаний, при этом расстояние между соседними максимумами волны составляет 1 м. Какова скорость распространения волны?
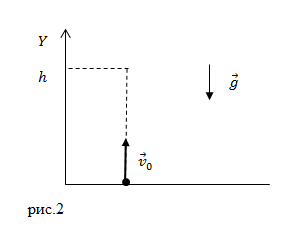
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для вычисления фазовой скорости волны вида:
Найдем период колебаний как время одного полного колебания:
Используя формулу (1.2) скорость будем вычислять, применяя формулу:
Вычислим искомую скорость:
Ответ. $v=5\frac<м><с>$
Задание. Уравнение плоской волны, которая распространяется вдоль положительного направления оси X, имеет вид: $\xi \left(x,t\right)=2<\cos \left[\omega \left(t-\frac
Решение. Фазовую скорость движения волны найдем как:
где период — величина обратная частоте колебаний:
Вычислим фазовую скорость:
\[v=450\cdot 0,8=360\ \left(\frac<м><с>\right).\]
Скорость колебания частиц равна:
Максимальное значение скорости колебаний частиц в волне из (2.3) равно:
Циклическую частоту найдем как:
Вычислим максимальную скорость колебаний частиц:
http://poisk-ru.ru/s63811t1.html
http://www.webmath.ru/poleznoe/fizika/fizika_142_formula_skorosti_volny.php