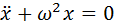Фазовые траектории дифференциальные уравнения excel

Фазовые портреты «на пальцах» или что можно узнать о решениях диффура, не решая его

Очень часто в ряде наук встречается ситуация, когда модель рассматриваемого процесса сводится к дифференциальному уравнению. Причём, в большинстве реальных задач это уравнение довольно сложно решить, или совсем невозможно. И вот тут в полный голос звучит извечный вопрос: как быть?

Встречайте: фазовые портреты (они же фазовые диаграммы). Простым языком, фазовый портрет — это то, как величины, описывающие состояние системы (a.k.a. динамические переменные), зависят друг от друга. В случае механического движения это координата и скорость, в электричестве это заряд и ток, в известной популяционной задаче это количество хищников и жертв и т.д.

Чем хороши фазовые портреты? А тем, что их можно построить не решая динамические уравнения системы. В некоторых случаях построение фазового портрета становится совсем простой задачей. Однако, одновременно с этим, фазовые портреты дают вдумчивому наблюдателю очень много информации о поведении системы.

Начнём с простого примера — малых колебаний (так же называемых гармоническими). Малые колебания встречаются почти в каждой сфере естественных наук. Для определённости, будем рассматривать колебания металлического стержня, подвешенного за один из концов (частный случай так называемого физического маятника). Можно показать, что его колебания описываются следующим дифференциальным уравнением:

Где x — угол отклонения стержня от вертикали, точка над x означает производную по времени, а коэффициент перед синусом зависит от размера и массы стержня.

Если амплитуда (размах) колебаний достаточно мала, синус можно приближенно заменить его аргументом (вы ведь помните первый замечательный предел, нет?). В таком случае, уравнение принимает следующий вид:

Это уравнение легко решается регулярными методами, но, давайте, попробуем применить к нему метод фазовых портретов. Для этого, домножим уравнение на производную и проинтегрируем его один раз по времени:

Получилось выражение, первый член которого выглядит как кинетическая энергия. Это не случайно — на самом деле мы получили именно закон сохранения энергии. Постоянная Е в правой части (полная энергия системы на единицу массы) может принимать различные значения, которые соответствуют разным начальным состояниям системы.

Полученный нами закон сохранения превратился в уравнение кривой на плоскости (x,u):

Для разных значений Е мы получим разные кривые. Нарисуем несколько таких линий для разных значений энергии:

По горизонтальной оси отложена величина x, по вертикальной — u

Каждая из полученных линий называется фазовой траекторией. Когда меняется состояние системы, изображающая её точка движется по одной из этих траекторий, стрелки указывают направление движения изображающей точки.

По графику видно, что значения скорости и координаты меняются циклическим образом, то есть периодически повторяются. Отсюда можно сделать вывод, что описываемая рассмотренным уравнением система будет совершать колебания. Бинго! Именно так ведёт себя маятник, и если решить уравнение, решение будет иметь вид периодических функций (а именно — комбинации синуса и косинуса).

Следует однако помнить, что замена синуса его аргументом оправдана лишь для малых углов отклонения (от 10 градусов и меньше), поэтому мы не можем доверять тем траекториям, которые выходят за границы области, ограниченной жирными пунктирными линиями, то есть из четырех приведенных траекторий лишь оранжевая достоверно отображает реальность. Кроме того, поскольку x это угол, то его значения, соответствующие 180 и -180 градусам описывают одно и то же положение стержня, то есть правая и левая пунктирные линии (тонкие) на графике это на самом деле одна и та же линия.

Теперь, поскольку нам понятна суть, можно перейти к чему-то посложнее. Выше мы очень сильно упростили уравнение и при этом ограничили себя только малыми колебаниями. Математик бы сказал, что мы линеаризовали уравнение и пренебрегли нелинейными эффектами. Так давайте включим в рассмотрение нелинейность. Вернёмся к самому первому уравнению — с синусом. Если мы повторим с ним то, что проделали с линейным уравнением, мы получим следующий закон сохранения:

В зависимости от значения энергии, мы опять получаем разные кривые, которые приведены на следующем рисунке, причем выбраны те же значения энергии, что и на первой диаграмме, и те же цвета для линий.

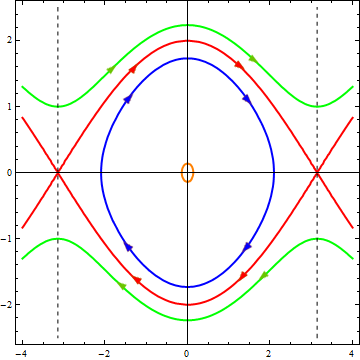
По горизонтальной оси отложена величина x, по вертикальной — u

Как видите, процессы происходящее в системе стали более разнообразными:

При малых энергиях (оранжевая и синяя траектории) существует колебательный режим, но колебания уже не являются гармоническими — фазовые траектории уже не имеют форму эллипсов.

При больших энергиях (зеленая траектория) колебаний уже нет, вместо этого мы получаем вращательное движение с переменной скоростью. И действительно, если достаточно сильно «толкнуть» стержень, он будет вращаться, замедляясь при подъёме и ускоряясь при спуске.

При определенном промежуточном значении энергии получается особый набор траекторий, которые отделяют друг от друга области соответствующие разным типам движения и поэтому называются сепаратрисами. И да, значение энергии для красной кривой было выбрано мной именно так, чтобы в нелинейном случае получилась сепаратриса. Каждая ветвь сепаратрисы это траектория, соответствующая особому типу движения. Посмотрим на диаграмму: движение начинается с очень маленькой скоростью от одного крайнего положения стержня, при приближении к положению равновесия скорость растёт, а после изображающая точка все более замедляясь уходит к крайнему положению, где и останавливается. Это соответствует тому, что мы поднимаем стержень вертикально вверх и отпускаем его, проносясь через положение равновесия он поднимается к верхней точке с другой стороны и останавливается.

А теперь давайте посмотрим насколько близки к истине наши выводы, сделанные на основе фазовых портретов. Перед вами график решения линейного уравнения:

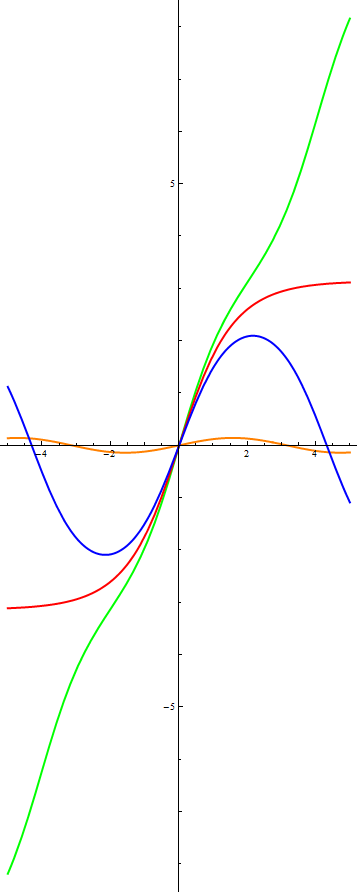
По горизонтальной оси отложено время, по вертикальной — x

Цветовая маркировка на этих графиках такая же, как и на фазовых портретах. Судить о том, насколько верные выводы были сделаны на основе фазовых портретов я предоставлю вам, дорогие читатели. Обращу ваше внимание только на один момент — колебания в линейном случае происходят синхронно — с одной и той же частотой. В нелинейном же случае, частота колебания с большей амплитудой (синяя линия) оказывается меньше, чем у колебания с малой амплитудой (оранжевая линия). Это служит еще одним подтверждением того, что нелинейные колебания не являются гармоническими.

Ну и напоследок: это всего лишь поверхностный экскурс в метод фазовых портретов, и словосочетание «на пальцах» попало в заголовок неспроста. Те же, кто решит углубиться в перипетии данного предмета, увидят, что за фазовыми портретами скрывается намного большее.

Основы метода фазовых траекторий

Исследование нелинейных систем автоматического управления связано с необходимостью составления и решения нелинейных дифференциальных уравнений. Поскольку единого общего решения для нелинейных дифференциальных уравнений разного вида не существует, то не представляется возможным создание обобщенного метода теории управления для исследования нелинейных систем, подобно случаю обыкновенных линейных систем.

Для исследования нелинейных систем в теории автоматического управления разработаны и используются частные методы, каждый из которых обладает определенными возможностями и эффективен в некоторой ограниченной области задач исследования. Наибольшее применение находят метод фазовых траекторий и амплитудно–частотный метод (метод гармонической линеаризации). Оба эти метода будут рассмотрены далее.

Метод фазовых траекторий заключается в том, что поведение исследуемой нелинейной системы рассматривается и описывается не во временной области (в виде уравнений процессов в системе), а в фазовом пространстве системы (в виде фазовых траекторий).

Состояние нелинейной системы автоматического управления характеризуется с использованием фазовых координат системы

задающих вектор состояния системы в фазовом пространстве системы

При введении в рассмотрение фазовых координат нелинейное дифференциальное уравнение порядка n для свободного процесса в нелинейной системе

преобразуется к системе из n дифференциальных уравнений первого порядка

В ходе процесса в системе фазовые координаты yi изменяются и вектор состояния системы Y описывает годограф в n– мерном фазовом пространстве системы (рис. 56). Годограф вектора состояния (траектория движения изображающей точки M, соответствующей концу вектора) есть фазовая траектория системы. Вид фазовой траектории однозначно связан с характером процесса в системе. Поэтому о свойствах нелинейной системы можно судить по ее фазовым траекториям.

Уравнение фазовой траектории может быть получено из приведенной выше системы уравнений первого порядка, связывающих фазовые координаты и учитывающих свойства системы, путем исключения времени. Фазовая траектория не отображает время процессов в системе.

Связь между фазовой траекторией y(x) и процессом x(t) поясняет рис. 57. Фазовая траектория построена в фазовых координатах 0XY, где x – выходная величина системы, y – скорость изменения выходной величины (первая производная x’). Переходный процесс x(t) построен в координатах x–t (выходная величина – время).

Пример. Рассмотрим в качестве примера систему, свободный процесс в которой описывается дифференциальным уравнением второго порядка

где u(t) выходная величина системы.

Введем в рассмотрение фазовые координаты x=u(t) и y=du/dt. Теперь систему можно описать с учетом фазовых координат

Чтобы получить уравнение фазовой траектории из приведенной системы уравнений необходимо исключить время. В рассматриваемом случае это можно сделать, разделив первое уравнение на второе

В результате получено дифференциальное уравнение первого порядка, функция решения которого y(x)+C, где C – постоянная интегрирования, описывает фазовую траекторию. Порядок полученного дифференциального уравнения ниже порядка исходного уравнения для процесса в системе, следовательно, решить это уравнение проще.

Фазовая траектория описывается дифференциальным уравнением, решения которого содержат постоянные интегрирования. Постоянные интегрирования зависят от начального состояния исследуемой системы в момент воздействия возмущения. Следовательно, система описывается множеством подобных фазовых траекторий, построенных для разных начальных условий и отличающихся разными значениями постоянной интегрирования C (рис. 58). Эта совокупность фазовых траекторий, построенных для системы при разных начальных условиях, получила название фазового портрета системы.

При использовании метода фазовых траекторий для исследования нелинейных систем необходимо строить и исследовать фазовые траектории. Практическое графическое построение фазовой траектории возможно только на фазовой плоскости, т.е. в случае описания исследуемой системы только двумя фазовыми координатами.

Указанное обстоятельство ограничивает возможность применения метода фазовых траекторий системами второго порядка. В случае описания исследуемой системы дифференциальным уравнением выше второго порядка, это уравнение приходится упрощать и сводить к уравнению второго порядка, что неизбежно ведет к возрастанию погрешности исследования.

Внастоящее время в связи с бурным развитием компьютерных технологий широкое применение получили специализированные математические пакеты программ, такие, как Ax

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

7.2.3. Построение фазовых портретов систем дифференциальных уравнений

Для дифференциального уравнения порядка выше первого команда DEplot представляет только кривые решений дифференциальных уравнений, а для систем дифференциальных уравнений первого порядка могут быть изображены и фазовые портреты.

С помощью команды DEplot можно построить фазовый портрет в плоскости ( x , y ), для системы двух дифференциальных уравнений: , если в параметрах данной команды указать scene=[x,y].

Если система дифференциальных уравнений является автономной, то на фазовом портрете будет отображено поле направлений в виде стрелок. Размер стрелок регулируется параметром arrows = SMALL , MEDIUM , LARGE , LINE или NONE .

Для того чтобы отобразить весь фазовый портрет, необходимо для каждой фазовой траектории указывать начальные условия: например, для системы двух дифференциальных уравнений первого порядка несколько начальных условий в команде DEplots указываются после задания диапазона изменения независимой переменной t: [[x(0)=x1, y(0)=y1], [x(0)=x2, y(0)=y2],…, [x(0)=xn, y(0)=yn]].

Начальные условия можно задавать в более компактной форме: [ t 0, x 0, y 0] , где t 0  точка, в которой задаются начальные условия; x 0 и y 0  значения искомых функций в точке t 0 .

Фазовый портрет системы двух дифференциальных уравнений первого порядка можно также построить с помощью команды phaseportrait ( sys , [ x , y ], x 1.. x 2,[[ cond ]]) , где sys  система двух дифференциальных уравнений первого порядка; [ x , y ]  имена искомых функций, x 1.. x 2  интервал, на котором следует построить фазовый портрет, а в фигурных скобках указываются начальные условия. Эта команда находится в пакете DEtools , поэтому данный пакет должен быть предварительно загружен.

Построить фазовый портрет системы дифференциальных уравнений: для нескольких наборов начальных условий (рис.7.7): х(0)=1, у(0)=0.2; х(0)=0, у(0)=1; х(0)=1, у(0)=0.4; х(0)=1, у(0)=0.75; х(0)=0, у(0)=1.5; х(0)=  0.1, у(0)=0.7.

[> restart; with(D Е tools):

Рис. 7.7. Фазовый портрет системы дифференциальных уравнений для нескольких наборов начальных условий

Построить фазовый портрет системы дифференциальных уравнений: . Начальные условия, диапазон изменения переменной и размеры координатных осей подбираются из соображений наглядности фазового портрета (рис. 7.8).

[> restart; with(D Е tools):

[[0,1,-2], [0,-3,-3], [0,-2,4], [0,5,5], [0,5,-3],[0,-5,2], [0,5,2], [0,-1,2]], x=-30..30, y=-20..20, stepsize=.1, colour=blue, linecolor=black);

Рис. 7.8. Фазовый портрет системы дифференциальных уравнений

8. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ, ВЕКТОРНЫЙ АНАЛИЗ, РЯДЫ, ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ

8.1. Дифференциальное исчисление функций многих переменных

Большинство задач дифференциального и интегрального исчисления функций многих переменных решается в Maple с помощью тех же команд, что и для функций одной переменной, только с указанием дополнительных опций.

8.1.1. Частные производные

Для вычисления частных производных функции f(x 1 ,…, x m ) используется команда:

где x1,…, xm – переменные, по которым производится дифференцирование, а после знака $ задается соответствующий порядок дифференцирования. Например, частная производная будет задана в виде: diff(f,x,y).

Найти и функции .

[> f := arctan ( x / y ):

Найти все частные производные 2-го порядка функции .

8.1.2. Локальные и условные экстремумы функций многих переменных

Для исследования функции нескольких пременных на локальный и условный экстремум используется команда из стандартной библиотеки extrema(f,,,’s’) , где cond – ограничения для поиска условного экстремума, которые записываются в виде неравенств или равенств. После ограничений в фигурных скобках указываются все переменные, от которых зависит функция f , а затем в кавычках записывается s – имя переменной, которой будут присвоены координаты точек экстремума. Для поиска локального экстремума множество задается пустым <> .

Отметим, что команда extrema выдает все критические точки, т.е. и те, в которых экстремума нет. Отсеять недающие экстремума критические точки можно с помощью подстановки этих точек в функцию, с использованием команды subs .

Как и для функции одной переменной, наибольшее и наименьшее значения функции нескольких переменных можно найти командами

в которых следует указывать после функции в фигурных скобках список всех переменных, от которых она зависит, и интервалы для каждой переменной, задающие область поиска наибольшего и наименьшего значений.

Если требуется найти переменные, при которых линейная функция многих переменных имеет максимум (или минимум) при наложении ограничений, заданных в виде линейных равенств или неравенств нужно использовать симплекс-метод. Для этого необходимо загрузить пакет simplex , а затем воспользоваться командой maximize (или minimize ), где в качестве range в фигурных скобках указывают ограничения.

Пакет simplex предназначен для решения задач линейной оптимизации. После его загрузки команды maximize и minimize выдают координаты точек, при которых заданная линейная функция имеет максимум или минимум. Для поиска неотрицательных решений используется команда NONNEGATIVE .

Найти экстремумы функции .

Получилось два экстремума, поэтому очевидно, что f max =0 и f min =  9/8, причем максимум достигается в точке (0,0). Остальные критические точки следует проверить. В силу четности функции по обеим переменным, можно ограничиться проверкой критических точек с положительными координатами.

Таким образом, функция имеет локальные экстремумы: f max = f (0,0)=0 и f min = f = f =9/8.

Найти наибольшее и наименьшее значения функции в прямоугольнике x = 0, y = 0, x = 1, y = 2.

Замечание: заданную область удобнее записывать в виде неравенств: 0 x 1, 0 y 2.

[> restart: readlib(maximize): readlib(minimize):

Таким образом, функция имеет наибольшее значение f max =17 и наименьшее значение f min =  4.

Найти условные экстремумы функции f ( х , у, z ) = xy + yz при x 2 + y 2 = 2, y + z = 2, x > 0, y > 0, z > 0.

[>restart: readlib(extrema): f:=x*y+y*z:

Несмотря на предварительное использование команды упрощения выражения simplify , полученный результат имеет не аналитический вид, однако это можно исправить, если воспользоваться командой convert .

= ,y

= , z

= >>

В этом случае команда extrema сама определила характер экстремумов, однако, в каких точках функция имеет экстремумы, можно определить подстановкой.

Таким образом, функция имеет следующие условные экстремумы: f max = f (1,1,1) = 2 и f min = f (1,1,1) = 0; третья критическая точка является седловой.

При каких значениях переменных функция f ( x , y , z ) =  x + 2 y + 3 z имеет максимум, если требуется выполнение условий x + 2 y  3 z  4, 5 x  6 y + 7 z  8, 9 x + 10 z  11, а все переменные неотрицательные?

Warning, new definition for maximize

Warning, new definition for minimize

8.2. Интегральное исчисление функций многих переменных

В Maple имеются две специальные команды для вычисления двойных и тройных интегралов из библиотеки student .

Для вычисления двойных интегралов используется команда Doubleint(f(x, y), D), где D – область интегрирования, записываемая в одном из следующих форматов:

– x=х1..х2, y=y1..y2 , где числа х1, х2, y1, y2 задают прямоугольную область интегрирования;

– x=f1(y)..f2(y), y=y1..y2 , где f1(y), f2(y)  линии, ограничивающие область интегрирования слева и справа на интервале от y1 до y2 ;

– x=х1..х2, y=g1(x)..g2(x) , где g1(y), g2(y)  линии, ограничивающие область интегрирования снизу и сверху на интервале от х1 до х2 .

Для вычисления тройных интегралов используется команда Tripleint(f(x, y, z),x, y, z, V), где V – область интегрирования.

Обе эти команды являются командами отложенного действия. Чтобы получить значение интеграла, следует использовать команду value(%).

Повторные интегралы можно вычислять с помощью повторения команды int , например, повторный интеграл вычисляется командой

Вычислить повторный интеграл

[> Int ( Int ( y ^3/( x ^2+ y ^2), x =0.. y ), y =2..4)=

Вычислить двойной интеграл по области, ограниченной линиями .

Замечание: вначале графически изобразим область интегрирования D (рис. 8.1.).

Warning, the name changecoords has been redefined

Рис. 8.1. Область интегрирования D , изображенная графически (красный треугольник)

Представим область интегрирования в виде неравенств:

Вычислить тройной интеграл .

Замечание: следует помнить, что порядок интегрирования определяется последовательностью пределов, поэтому сначала указываются внутренние пределы.

8.3. Векторный анализ

Основные дифференциальные операции векторного анализа и команды Maple для их вычисления, содержатся в библиотеке linalg .

Градиент скалярной функции f(x,y,z) – это вектор, координатами которого являются частные производные по соответствующим переменным: . В Maple вычисляется командой grad(f,[x,y,z], c ) , где f – функция, [x,y,z] – набор переменных, от которых она зависит.

Опция с позволяет вычислять данную дифференциальную операцию в различных криволинейных координатах (по умолчанию используется прямоугольная декартова система координат). Этот параметр может указываться во всех имеющихся в Maple дифференциальных операциях. Для вычисления дифференциальной операции в цилиндрических координатах следует записать coords = cylindrical , в сферических координатах – coords = spherical .

Лапласиан скалярной функции f(x,y,z) – это оператор, действующий на функцию f ( x , y , z ) по следующему правилу: . Он вычисляется командой laplacian(f,[x,y,z],опция) .

Дивергенцией вектор-функции F(x,y,z) называется функция (скалярная), вычисляемая по правилу: . Дивергенция в Maple вычисляется командой diverge(F,[x,y,z],опция), где F – вектор-функция; [x,y,z] – набор переменных, от которых она зависит.

Ротором вектор-функции F(x,y,z) называется вектор с координатами: . Ротор вычисляется командой curl(F,[x,y,z], c ).

Для вектор-функции F(x,y,z) можно вычислить матрицу Якоби

с помощью команды jacobian(F,[x,y,z]).

Дана функция . Найти . Определить углы, которые составляют с осями координат. Найти производную функции u(x,y) по направлению вектора q=[1,1].

Warning, new definition for norm

Warning, new definition for trace

[>u:=arctan(y/x): g:=simplify(grad(u, [x, y]));

[> alpha:=simplify(angle(g, [1, 0]));

[> beta:=simplify(angle(g, [0, 1]));

Косинусы полученных углов являются направляющими косинусами . Легко убедиться, что сумма их квадратов равна единице.

Производная функции u по направлению q равна скалярному произведению градиента этой функции на нормированный вектор q : , где  нормированный вектор q .

е :=

udq:=

Дана вектор-функция F(x,y,z)=. Найти и .

[> divF:=diverge(F, [x, y, z]);

При каком значении параметра а функция u = x 3 + axy 2 удовлетворяет уравнению Лапласа  u=0 ?

 (x 3 +axy 2 ):=6x+2ax

Доказать, что функция , где удовлетворяет дифференциальному уравнению , k  постоянная.

[> Delta(u):=simplify(laplacian(u, [r, theta, phi], coords=spherical));

Найти матрицу Якоби и ее определитель вектор-функция v =[ x , y / x ].

[> v:=vector([x, y/x]): jacobian(v, [x, y]);

8.4. Ряды и произведения

8.4.1. Вычисление суммы ряда и произведений

Конечные и бесконечные суммы вычисляются командой прямого исполнения sum и отложенного исполнения Sum . Форматы этих команд одинаковы: sum(expr, n=a..b) , где expr – выражение, зависящее от индекса суммирования; a..b – пределы индекса суммирования, указывающие, что суммировать следует от n=a до n=b .