Фазовый портрет дифференциального уравнения второго порядка онлайн

Фазовые портреты линейных систем второго порядка

Дата добавления: 2014-04-22 ; просмотров: 7084 ; Нарушение авторских прав

Для получения уравнений, описывающих фазовый портрет системы второго порядка, необходимо в системе дифференциальных уравнений (12.6) второе уравнение поделить на первое и исключить из рассмотрения время t, в результате чего получают:

. (13.3)

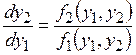
Решение этого уравнения дает семейство интегральных кривых на фазовой плоскости, по которым строят фазовые траектории системы.

Фазовые портреты линейных систем второго порядка классифицируют по типам особых точек.

Линейную систему второго порядка описывают уравнением

, (13.4)

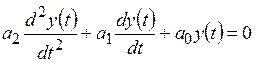
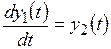
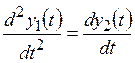
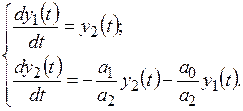
где y(t) − выходная координата системы; а₀, а₁, a₂ − постоянные коэффициенты. Обозначив y(t) = y₁(t), , тогда и уравнение (13.1) можно записать

(13.5)

Разделив второе уравнение на первое, получают

, (13.6)

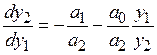
решением которого будет уравнение фазовых траекторий

где с_i − постоянные интегрирования.

Возможны шесть различных типов фазовых траекторий в зависимости от корней характеристического уравнения a₂s 2 + a₁s + a₀ = 0.

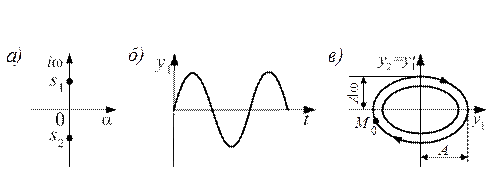
Случай 1. Корни − мнимые при a₁=0, a₀>0, a₂>0; s_1,2=±iω; .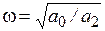

Система находится на границе устойчивости.

График y₁(t) показан на рис. 13.1. Для получения уравнения фазовой траектории выражения (13.8) и (13.9) возводят в квадрат и складывают, в результате получают уравнение

. (13.10)

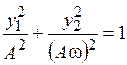
Незатухающим периодическим колебаниям в системе соответствует на фазовой плоскости замкнутая фазовая траектория. Особая точка системы является геометрическим центром фазовых траекторий и носит название центр, а сама система называется консервативной.

Рис. 13.1. Фазовый портрет типа центр: а) плоскость корней

характеристического уравнения; б) переходный процесс; в) фазовый портрет

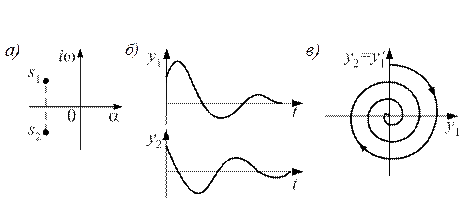
Случай 2. Корни − комплексные и имеют отрицательные вещественные части при а₁ 0, a₁ > 0, а₂ > 0: s₁,₂ = −α ± iω (рис. 13.2а),

α = −a₁/(2а₂), 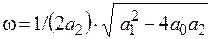− система устойчива.

Решение уравнения (13.4) имеет вид

где d = arctg(a/w); .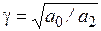

Рис. 13.2. Фазовый портрет типа устойчивый фокус: а) расположение корней

характеристического уравнения; б) переходный процесс; в) фазовый портрет

Уравнения (13.11) и (13.12) дают в фазовой плоскости параметрическое уравнение спиралей. С каждым оборотом, соответствующим одному периоду колебаний, изображающая точка приближается к началу координат, так как значения y₁ и y₂за период колебаний становятся меньше.

Особая точка называется устойчивым фокусом.

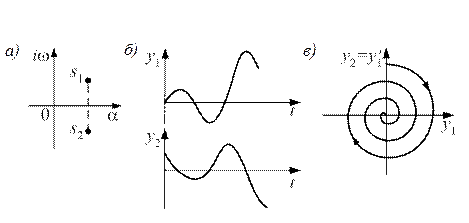
Случай 3.Корни − комплексные и имеют положительные вещественные части при а₁ 0, a₁ 0: s₁,₂ = α ± iω (рис. 13.3а), система неустойчива. Откуда

Рис. 13.3 Фазовый портрет типа неустойчивый фокус: а) расположение корней

характеристического уравнения; б) переходный процесс; в) фазовый портрет

Состоянию неустойчивого равновесия системы соответствует особая точка, которая называется неустойчивый фокус (рис. 13.3в). В системе возникает колебательный процесс с возрастающей амплитудой.

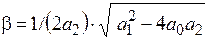
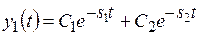
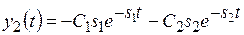
Случай 4. Корни – вещественные отрицательные при а₁ > 4а₀a₂; a₀ > 0, a₁ > 0, а₂ > 0: s₁,₂ = −α±b (рис. 13.4а), α = a₁/(2а₂), − система устойчива. Этот случай соответствует апериодическому процессу в системе, сама система устойчива. Решение уравнения (13.14)

; (13.15)

. (13.16)

Границей областей с переходными процессами типа 1 и 2 служат прямые с уравнениями y₂ = −s₂y₁ и y₂ = −s₁y₁.

Все фазовые траектории вливаются в начало координат − особую точку, называемую устойчивым узлом (рис. 13.4). Время движения к состоянию равновесия теоретически равно бесконечности.

Рис. 13.4. Фазовый портрет типа устойчивый узел: а) расположение корней

характеристического уравнения; б) переходный процесс; в) фазовый портрет

Случай 5. Корни − вещественные положительные при а₁>4а₀a₂; a₀>0, a₁ 0: s₁,₂ = α ± b (рис. 13.5а), система неустойчива. Решение уравнения (13.4):

; (13.17)

. (13.18)

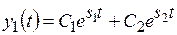
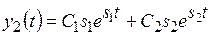
Рис. 13.5. Фазовый портрет типа неустойчивый узел: а) расположение корней

характеристического уравнения; б) переходный процесс; в) фазовый портрет

Фазовые траектории направлены от начала координат в бесконечность. Особая точка носит название неустойчивый узел (рис. 13.5). Крайние траектории определяются уравнениями y₂ = s₁y₁ и y₂ = s₂y₁.

Случай 6. Корни − вещественные и имеют различные знаки при a₀ 0, a₂ > 0: s₁ = −α₁, s₂ = β. В этом случае система неустойчива.

Частным является случай, когда a₁=0, и, учитывая, что a₀

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Решение дифференциальных уравнений онлайн

Дифференциальным уравнением называется уравнение которое связывает неизвестную функцию и её производные различных порядков:

F ( x , y ‘ , y » , . , y ( n ) ) = 0

Порядком дифференциального уравнения называется порядок его старшей производной. Решить дифференциальное уравнение, значит найти неизвестную функцию , которая обращает это уравнение в верное тождество. Этого можно достичь, изучив теоретический материал по дифференциальным уравнениям, или воспользовавшись нашим онлайн калькулятором.

Наш калькулятор может находить как общее решение дифференциального уравнения, так и частное. Для поиска частного решения, необходимо ввести начальные условия в калькулятор. Для поиска общего решения, поле ввода начальных условий необходимо оставить пустым.