Фиктивные переменные уравнении множественной регрессии

Фиктивные переменные во множественной регрессии

До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т. е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными. В отечественной литературе можно встретить термин «структурные переменные».

Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для совокупности обследуемых уравнение регрессии имеет вид:

,

где — количество потребляемого кофе; — цена.

Аналогичные уравнения могут быть найдены отдельно для лиц мужского пола: и женского пола: .

Различия в потреблении кофе проявятся в различии средних и . Вместе с тем сила влияния на может быть одинаковой, т. е. . В этом случае возможно построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной. Объединив уравнения и и введя фиктивные переменные, придем к следующему выражению: ,

где и – фиктивные переменные, принимающие значения:

В общем уравнении регрессии зависимая переменная рассматривается как функция не только цены , но и пола . Переменная рассматривается как дихотомическая переменная, принимающая всего два значения: 1 и 0. При этом когда , то и, наоборот, при переменная .

Для лиц мужского пола, когда и , объединенное уравнение регрессии составит: , а для лиц женского пола, когда и . Иными словами, различия в потреблении для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии: . Параметр является общим для всей совокупности лиц, как для мужчин, так и для женщин.

Следует иметь в виду, что при введении фиктивных переменных и в модель применение МНК для оценивания параметров а₁ и а₂ приведет к вырожденной матрице исходных данных, а следовательно, и к невозможности получения их оценок. Объясняется это тем, что при использовании МНК в данном уравнении появляется свободный член, т. е. уравнение примет вид

Предполагая при параметре А независимую переменную, равную 1, имеем матрицу исходных данных:

В рассматриваемой матрице существует линейная зависимость между первым, вторым и третьим столбцами: первый равен сумме второго и третьего столбцов. Поэтому матрица исходных факторов вырождена. Выходом из создавшегося затруднения может явиться переход к уравнению

,

т.е. каждое уравнение включает только одну фиктивную переменную z₁ или z₂.

В рассмотренном примере качественный фактор имел только два состояния, которым и соответствовали обозначения 1 и 0. Если же число градаций качественного признака-фактора превышает два, то в модель вводится несколько фиктивных переменных, число которых должно быть меньше числа качественных градаций. Только при соблюдении этого положения матрица исходных фиктивных переменных не будет линейно зависима и возможна оценка параметров модели.

Резюме по теме.

Зависимость между большинством экономических переменных не является строго функциональной из-за воздействия случайных незначительных факторов, и каждому значению одной переменной соответствует множество возможных значений другой переменной. Поэтому исследователи рассматривают зависимость между значениями одной переменной и условным математическим ожиданием другой. Такая зависимость называется корреляционной или регрессионной. Зависимость условного математического ожидания СВ Y от X называется модельным уравнением регрессии. Эта регрессия строится по генеральной совокупности. Но обычно исследователи имеют дело лишь с конечной выборкой ограниченного объема, поэтому вместо модельного уравнения регрессии используют выборочное уравнение регрессии, характеризующее зависимость выборочного условного среднего от х. Параметры спецификации выборочной регрессии являются оценками соответственных параметров спецификации модельной регрессии. В общем случае не известны ни точный вид функции, ни значения параметров спецификации.

Вопросы для повторения

2. Что такое условное математическое ожидание?

3. Какая зависимость называется корреляционной или регрессионной?

4. Что такое объясняющая переменная?

5. Что такое объясняемая переменная?

6. Какое уравнение называется модельным уравнением регрессии?

7. Какое уравнение называется выборочным уравнением регрессии?

8. Какая модель наблюдения соответствует модельному уравнению регрессии?

9. Какая модель наблюдения соответствует выборочному уравнению регрессии?

10. Что такое величины e_i?

11. Что такое невязки, остатки?

12. Задачи регрессионного анализа?

13. Что такое парная линейная регрессия?

14. Что такое принцип наименьших квадратов?

15. Что такое метод наименьших квадратов (МНК)?

16. Применение МНК для вычисления коэффициентов парной линейной регрессии?

17. Нормальные уравнения для вычисления коэффициентов парной линейной регрессии?

18. Как оценить статистическую значимость уравнения регрессии в целом?

19. Как оценить статистическую значимость параметров регрессии?

20. Прогноз по уравнению парной линейной ререссии

21. Что такое гомоскедастичность остатков?

22. Что такое гетероскедастичность остатков?

23. Виды нелинейной регрессии

24. Оценка тесноты связи нелинейной регрессии

25. Оценка статистической значимости нелинейной регрессии

26. В каких случаях целесообразно использование множественной регрессии?

27. Требования, предъявляемые к факторам, включаемым во множественную регрессию

28. Мультиколлинеарность, способы ее выявления и ее коррекции

29. Уравнение линейной множественной регрессии. Коэффициенты «чистой» регрессии

30. Стандартизованные уравнения регрессии. Стандартизованные коэффициенты регрессии

31. Частные уравнения регрессии

32. Частные коэффициенты корреляции

33. Предпосылки МНК, методы их проверки

34. Свойства оценок МНК

35. Оценка статистической значимости множественной регрессии в целом

36. Оценка статистической значимости коэффициентов «чистой» регрессии

37. Фиктивные переменные во множественной регрессии

Фиктивные переменные в регрессионной модели 1 страница

В линейную модель множественной регрессии, как правило, включаются количественные факторы X₁, X₂, …, X_p, принимающие значения из некоторого интервала, непрерывного либо дискретного. Однако может возникнуть необходимость учесть влияние на зависимую переменную Y и факторов, не измеряемых в числовой шкале (например, формы собственности предприятия, сезонности, региона, климатических условий, пола работника, его уровня образования и т.п.). Такие качественные факторы могут иметь два и более атрибута (градации). Чтобы ввести качественный фактор в регрессионную модель, его необходимо преобразовать в количественную переменную, т.е. присвоить каждому атрибуту те или иные числовые значения. Эту преобразованную переменную называют фиктивной (условной), а модель регрессии, включающую в себя хотя бы одну фиктивную переменную, называют моделью с переменной структурой. Основной целью построения такой модели является учет влияния неоднородности качественной структуры исследуемой совокупности.

В качестве фиктивных обычно используют бинарные переменные, принимающие только два значения (уровня): «0» или «1». Такие переменные также называются двоичными, дихотомическими, альтернативными, или булевыми. К примеру, если необходимо изучить зависимость общей рентабельностипредприятия Y не только от количественных факторов X₁, X₂, …, X_p, но и от фактора «форма собственности», то в модель вводят фиктивную переменную Z₁, принимающую значения: z₁=1 — если предприятие негосударственное и z₁=0 — если предприятие государственное.

Регрессионная модель рентабельности, в этом случае, примет вид:

.

(3.58)

Параметр регрессии g₁ при фиктивной переменной Z₁ показывает, на сколько в среднем рентабельность негосударственных предприятий в исследуемой совокупности выше, чем государственных при неизменных значениях остальных факторов X₁, X₂, …, X_p. Если не учитывать различия, связанные с формой собственности, то они могут либо уйти в остаточную вариацию результата Y, ухудшив модель, либо смешаться с влиянием тех или иных количественных факторов, искажая меру их влияния на Y.

В модель множественной регрессии можно одновременно ввести несколько фиктивных переменных Z₁, Z₂, …, Z_u:

.

(3.59)

Обычно значение, равное единице, присваивают фиктивной переменной для той группы исследуемых объектов, у которых значение результата Y предположительно в среднем выше, чем у объектов альтернативной группы. Положительный знак коэффициента уравнения регрессии при фиктивной переменной и его статистическая значимость в дальнейшем подтверждают это предположение. При отрицательном знаке следует сделать обратный вывод.

Применение фиктивной переменной с другими значениями или с большим числом уровней затрудняет содержательную экономическую интерпретацию соответствующего коэффициента уравнения регрессии. Например, если число k уровней качественного признакаболее двух ( ), то в принципе в регрессионную модель можно было бы ввести дискретную переменную, принимающую такое же количество значений. Так, если расширить трактовку фактора «форма собственности» до трех групп: государственные, кооперативные и частные предприятия, то при построении модели рентабельности можно рассматривать три значения (k=3) фиктивной переменной Z₁, например: z₁=1 — если предприятие государственное, z₁=2 — если кооперативное, и z₁=3 — если частное. Однако содержательная интерпретация коэффициента уравнения регрессии при Z₁ тогда будет невозможна. Вместо этого в модель следует ввести бинарных переменных и для учета влияния формы собственности включают бинарные переменные — Z₁₁ и Z₁₂:

,

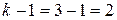
(3.60)

где z₁₁=1 — если предприятие частное, z₁₁=0 — во всех остальных случаях; z₁₂=1 — если предприятие кооперативное, z₁₂=0 — во всех остальных случаях.

Третьей бинарной переменной, очевидно, не требуется: еслипредприятие государственное, то это будет отражено парой значений z₁₁=0 и z₁₂=0. Более того, вводить третью бинарную переменную Z₁₃ со значениями z₁₃=1, если предприятие государственное и z₁₃=0 — в остальных случаях, нельзя, так как это приведет к невозможности получения оценок параметров модели при фиктивных переменных методом наименьших квадратов.

Параметры модели при Z₁₁ и Z₁₂ интерпретируются следующим образом. Параметр g₁₁ показывает, на сколько средняя рентабельность частных предприятий при прочих равных условиях выше средней рентабельности государственных предприятий, которые приняты за базу для сравнения. Аналогично параметр g₁₂ показывает превышение средней рентабельности кооперативных предприятий над этим показателем у государственных предприятий.

Модели регрессии (3.58) — (3.60) называются моделями без ограничений. Если значения каких-либо фиктивных переменных равны нулю, то получаются частные модели регрессии. Так, если в модели (3.60) все значения фиктивных переменных равны нулю: z₁₁=0 и z₁₂=0, то получается модель (3.2), которая в этом случае называется базисной моделью, или моделью регрессии с ограничениями. Данная модель является частной моделью государственного предприятия. Частная модель регрессии частного предприятия (z₁₁=1, z₁₂=0) образуется путем добавления параметра g₁₁ к свободному коэффициенту b₀:

.

(3.61)

Аналогично частная модель кооперативного предприятия (z₁₁=0, z₁₂=1):

.

(3.62)

На практике могут использоваться регрессионные модели только с фиктивными переменными-факторами. Пусть, например, изучаются различия в средней стоимости квадратного метра общей площади квартиры (переменная Y), в зависимости от района города, типа дома и этажа (фиктивные переменные Z₁, Z₂ и Z₃ соответственно). Модель регрессии в этом случае может иметь вид:

,

(3.63)

где z₁=1 — если дом расположен в центральном районе города, z₁=0 — если дом расположен в периферийном районе; z₂=1 — если дом кирпичный, z₂=0 — если дом панельный; z₃=1 — если квартира расположена на средних этажах, z₃=0 — если квартира расположена на крайних этажах.

Базисной моделью здесь является модель средней стоимости квадратного метра квартиры на крайних этажах (z₃=0) в панельном доме (z₂=0), расположенном в периферийном районе города (z₁=0). Параметр g₀ модели (3.63) и показывает среднюю стоимость квадратного метра такой квартиры. Параметр g₁ характеризует разницу в средней стоимости квадратного метра квартир, расположенных в центральном и периферийном районах города, параметр g₂ — эту разницу в зависимости от типа дома, параметр g₃ — в зависимости от этажа.

Параметры модели с фиктивными переменными оцениваются по исходным данным обычным методом наименьших квадратов. Предварительно следует провести проверку на коллинеарность, причем как фиктивных переменных между собой, так и фиктивных переменных с количественными факторами (см. § 3.4).

Уравнение регрессии модели (3.59) выглядит следующим образом:

,

(3.64)

После построения уравнения регрессии проверяется его статистическая значимость в целом и значимость отдельных коэффициентов соответственно по критериям Фишера и Стьюдента. Значимость коэффициента при фиктивной переменной на принятом уровне значимости a свидетельствует о существенном (значимом) различии между значениями результата Y для разных уровней фиктивной переменной и, соответственно, групп исследуемых объектов.

Если значимость коэффициентапри фиктивной переменной не установлена, то разница между градациями соответствующего качественного фактора признается несущественной. Если значение t-статистики при этом превышает по абсолютной величине единицу, то фиктивная переменная все же может считаться в какой-то степени информативной. Однако, если t-статистика по абсолютной величине меньше единицы, то соответствующую фиктивную переменную следует исключить из модели и заново построить уравнение регрессии уже без нее. Следует, однако, учитывать, что незначимость коэффициента при фиктивной переменной может быть вызвана и недостаточным объемом выборки.

Возвратимся к рассмотренным выше примерам. Пусть строится модель с одной фиктивной переменной (3.58) и уравнение регрессии будет иметь вид:

.

(3.65)

Если коэффициент g₁ признается статистически значимым на принятом уровне a, то это означает, что разница между рентабельностью частных и государственных предприятий в исследуемой совокупности признается существенной, а фиктивная переменная Z₁ введена в модель обоснованно.

Пусть, к примеру, исследуется зависимость рентабельности однородных предприятий (зависимая переменная Y, %) от стоимости основных фондов (фактор X₁, млн. руб.) и формы собственности (фиктивная переменная Z₁: z₁=1— если предприятие негосударственное, z₁=0 — если предприятие государственное), и по имеющимся данным было получено уравнение регрессии

.

Базисной моделью здесь является модель рентабельности государственного предприятия (z₁=0), уравнение регрессии которой

.

Предположим, что коэффициент при фиктивной переменной Z₁ оказался статистически значимым на принятом уровне a=0,05. Тогда можно утверждать, что рентабельность негосударственных предприятий в среднем на 4,34 % выше, чем государственных. Коэффициент регрессии при переменной X₁ показывает, что рост стоимости основных фондов на 1 млн. руб. приводит в среднем к снижению рентабельности на 0,032 % как государственных, так и негосударственных предприятий.

Уравнение регрессии модели (3.60) выглядит следующим образом:

.

(3.66)

Пусть, к примеру, коэффициент g₁₁ оказался статистически значимым, а коэффициент g₁₂ — незначимым. Тогда разница между рентабельностью частных и государственных предприятий признается существенной, а разница между рентабельностью кооперативных и государственных предприятий — несущественной. Если t-статистика коэффициента g₁₂ при этом по абсолютной величине меньше единицы, то фиктивную переменную Z₁₂ следует исключить из модели и перейти к построению модели с одной фиктивной переменной (3.58).

Допустим, исследуется зависимость рентабельности однородных предприятий (зависимая переменная Y, %) от стоимости основных фондов (переменная X₁, млн. руб.) и формы собственности (бинарные переменные Z₁₁ и Z₁₂: z₁₁=1 — если предприятие частное, z₁₁=0 — во всех остальных случаях; z₁₂=1 — если предприятие кооперативное, z₁₂=0 — во всех остальных случаях), и было построено уравнение регрессии

.

Видно, что рост стоимости основных фондов на 1 млн. руб. приводит к снижению рентабельности всех предприятий в среднем на 0,028 %.

Базисной моделью здесь является модель рентабельности государственного предприятия (z₁₁=0, z₁₂=0), для которой уравнение регрессии

.

Пусть коэффициенты при фиктивных переменных Z₁₁ и Z₁₂ оказались статистически значимыми на принятом уровне a=0,05. Уравнение регрессии частной модели рентабельности частного предприятия (z₁₁=1, z₁₂=0) примет вид:

.

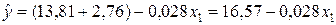
Таким образом, средняя рентабельность частных предприятий при одинаковой стоимости основных фондов на 2,76 % выше средней рентабельности государственных предприятий.

Аналогично для кооперативных предприятий (z₁₁=0, z₁₂=1) уравнение регрессии частной модели

.

Видно, что рентабельность кооперативных предприятий оказалась в среднем на 1,98 % выше рентабельности государственных предприятий.

Разница между коэффициентами при фиктивных переменных Z₁₁ и Z₁₂ — %, показывает, на сколько в среднем рентабельность частных предприятий выше рентабельности кооперативных предприятий.

Уравнение регрессии модели только с фиктивными переменными (3.63) будет иметь вид:

.

(3.67)

Пусть, например, по имеющимся данным было получено уравнение регрессии модели средней стоимости квадратного метра квартиры

,

и все коэффициенты при фиктивных переменныхоказались статистически значимыми на принятом уровне a. Эти коэффициенты интерпретируются следующим образом: средняя стоимость квадратного метра квартиры на крайних этажах (z₃=0) в панельном доме (z₂=0), расположенном в периферийном районе города (z₁=0), составляет 532,1 у.е.; если дом располагается в центральном районе, то средняя стоимость квадратного метра возрастает на 187,6 у.е.; кирпичный дом дополнительно повышает среднюю стоимость квадратного метра на 142,4 у.е., а расположение квартиры на средних этажах — на 92,3 у.е.

Следует иметь в виду, что надежные оценки параметров модели (3.63) могут быть получены только при построении уравнения регрессии по достаточно большому числу наблюдений. Обычно при построении такой модели объем выборки должен превышать число факторов в шесть и более раз.

Решение типовых задач

Пример 3.1

Изучается зависимость чистой годовой прибылистраховой компании (зависимая переменная Y, тыс. руб.) от следующих факторов:

· X₁ — годовой размер собственных средств (тыс. руб.);

· X₂ — годовой размер страховых резервов (тыс. руб.);

· X₃ — годовой размер страховых премий (тыс. руб.);

· X₄ — годовой размер страховых выплат (тыс. руб.);

· X₅ — численность страховых агентов;

· X₆ — форма собственности (0 — государственная, 1 — частная):

1. Составить матрицу парных коэффициентов корреляции между всеми исследуемыми переменными и выявить коллинеарные факторы.

2. Построить уравнение линейной регрессии с полным перечнем факторов. Оценить статистическую значимость уравнения и его коэффициентов с помощью критериев Фишера и Стьюдента.

3. Построить уравнение регрессии, не содержащее коллинеарных факторов. Проверить статистическую значимость уравнения и его коэффициентов.

4. Построить уравнение регрессии, содержащее только информативные факторы. Проверить статистическую значимость уравнения и его коэффициентов.

Пункты 5 — 9 относятся к уравнению регрессии, построенному при выполнении пункта 4.

5. Оценить качество и точность уравнения регрессии.

6. Дать экономическую интерпретацию коэффициентам уравнения регрессии и сравнительную оценку силы связи факторов с результатом.

7. Построить график остатков и проверить выполнение предпосылок обычного метода наименьших квадратов.

8. Рассчитать прогнозное значение годовой прибыли Y, если прогнозные значения факторов составят 75 % от своих максимальных значений.

9. Построить доверительный интервал прогноза фактического значения годовой прибыли Y c надежностью 80 %.

Для решения задачи используем табличный процессор EXCEL.

1. С помощью надстройки «Анализ данных… Корреляция» (см. § 5.2) строим матрицу парных коэффициентов корреляции между всеми исследуемыми переменными (табл. 3.3).

Анализ значений коэффициентов корреляции между парами факторов Х₁, Х₂, …, Х₆ показывает, что только коэффициент корреляции между факторами Х₁ и Х₃ превышает по абсолютной величине 0,8 (выделен в таблице заливкой). Факторы Х₁ и Х₃ являются, таким образом, коллинеарными.

2. С помощью надстройки «Анализ данных… Регрессия» (см. § 5.3) строим уравнение линейной регрессии с полным перечнем факторов. Результаты регрессионного анализа в EXCEL приведены в табл. 3.4. Уравнение регрессии с полным перечнем факторов имеет вид:

.

Проверим статистическую значимость уравнения регрессии. Табличное значение F-критерия Фишера можно определить с помощью встроенной функции EXCEL «FРАСПОБР» (см. § 5.4). Для уровня значимости a=0,05 и чисел степеней свободы числителя (регрессии) (где p=6 — число факторов в модели) и знаменателя (остатка) табличное оно составляет F_таб=2,60.

Видно, что расчетное значение F-статистики Фишера

превышает табличное (см. «F» втабл. 3.4), что свидетельствует о статистической значимости уравнения регрессии в целом. На этот же факт указывает и то, что вероятность случайного формирования уравнения регрессии в том виде, в котором оно имеется, составляет 8,20×10 -6 (см. «Значимость F» втабл. 3.4), что ниже допустимого уровня значимости a=0,05.

Проверим статистическую значимость коэффициентов уравнения регрессии при факторах Х₁, Х₂, …, Х₆ с помощью t-критерия Стьюдента:

.

Табличное значение t-критерия Стьюдента можно определить с помощью встроенной функции EXCEL «СТЬЮДРАСПОБР» (см. § 5.4). Для уровня значимости a=0,05 и числа степеней свободы остатка df=df_ост=20 оно составляет t_таб=2,086. Анализ данных в табл. 3.4показывает, что табличное значение t‑критерия Стьюдента превышают по абсолютной величине t-статистики коэффициентов при факторах Х₄, Х₆, и эти коэффициенты признаются статистически значимыми. На тот же самый факт указывают и значения вероятности случайного формирования коэффициентов, которые ниже допустимого уровня значимости a=0,05 (см. «P-Значение»втабл. 3.4).

Что касается факторов Х₁, Х₂, Х₃ и Х₅ (выделены в табл. 3.4 заливкой), то t‑статистики их коэффициентов меньше по абсолютной величине табличного значения t-критерия Стьюдента, а «P-Значение» выше уровня a=0,05. Данные коэффициенты не признаются статистически значимыми.

Построение регрессионных моделей с фиктивными переменными

ПОСТРОЕНИЕ РЕГРЕССИОННЫХ МОДЕЛЕЙ С ФИКТИВНЫМИ ПЕРЕМЕННЫМИ

В регрессионных моделях в качестве объясняющих переменных часто приходится использовать не только количественные (определяемые численно), но и качественные переменные. Например, спрос на какое-либо благо может определяться как количественными переменными (цена данного блага), так и качественными (вкусы потребителей). Качественные показатели в численном виде представить нельзя. Возникает проблема отражения в модели влияния таких переменных на исследуемую величину.

Обычно в моделях влияние качественного фактора выражается в виде фиктивной (искусственной) переменной, которая отражает два противоположных состояния качественного фактора. В этом случае фиктивная переменная может выражаться в двоичной форме:

Переменная D называется фиктивной (искусственной, двоичной) переменной (индикатором).

Регрессионные модели, содержащие лишь качественные объясняющие переменные, называются моделями дисперсионного анализа (ANOVA-моделями).

Тогда зависимость можно выразить моделью парной регрессии:

.

Коэффициент определяет среднюю начальную заработную плату при отсутствии высшего образования. Коэффициент указывает, на какую величину отличаются средние начальные заработные платы при наличии и при отсутствии высшего образования у претендента. Проверяя статическую значимость коэффициента с помощью t-статистики, либо значимость коэффициента детерминации или F-статистики, можно определить, влияет или нет наличие высшего образования на начальную заработную плату.

Модели, в которых объясняющие переменные носят как количественный, так и качественный характер, называются моделями ковариационного анализа (ANCOVA-моделями).

Существует несколько разновидностей моделей ковариационного анализа.

1. Модели ковариационного анализа при наличии у фиктивной переменной двух альтернатив.

Рассмотрим простейшую модель с одной количественной и одной качественной переменными, имеющую два альтернативных состояния:

.

Пусть, например, Y – заработная плата сотрудника фирмы, х – стаж сотрудника, D – пол сотрудника, т. е.

Тогда ожидаемое значение заработной платы сотрудников при х годах трудового стажа будет:

Заработная плата в данном случае является линейной функцией от стажа работы.

При составлении моделей с фиктивными переменными необходимо руководствоваться следующим правилом моделирования: если качественная переменная имеет k альтернативных значений, то при моделировании используется (k – 1) фиктивных переменных. Таким образом, если переменная имеет два альтернативных значения (например, пол), то в модель можно ввести только одну фиктивную переменную.

Если не следовать данному правилу, то при моделировании исследователь попадает в ситуацию совершенной мультиколлинеарности или так называемую ловушку фиктивной переменной.

Значение качественной переменной, для которого принимается D = 0, называется базовым или сравнительным. Выбор базового значения обычно диктуется целями исследования, но может быть и произвольным.

Коэффициент в модели иногда называется дифференциальным коэффициентом свободного члена, так как он показывает, на какую величину отличается свободный член модели при значении фиктивной переменной, равном единице, от свободного члена модели при базовом значении фиктивной переменной.

2. Модели ковариационного анализа при наличии у качественных переменных более двух альтернатив.

Рассмотрим модель с двумя объясняющими переменными, одна из которых количественная, а другая – качественная. Причем качественная переменная имеет три альтернативы. Например, расходы на содержание ребенка могут быть связаны с доходами домохозяйства и возрастом ребенка: дошкольный, младший школьный и старший школьный. Так как качественная переменная имеет три альтернативы, то по общему правилу моделирования необходимо использовать две фиктивные переменные. Таким образом, модель может быть представлена в виде:

,

где Y – расходы, x – доходы домохозяйств.

Образуются следующие зависимости:

1. Средний расход на дошкольника:

(1)

2. Средний расход на младшего школьника:

(2)

3. Средний расход на старшего школьника:

(3)

Здесь γ1, γ2 – дифференциальные свободные члены. Базовым значением качественной переменной является значение «дошкольник». После вычисления коэффициентов уравнений регрессии (1) – (3) определяется статистическая значимость коэффициентов γ1и γ2 на основе обычной t-статистики.

Если коэффициенты γ1 и γ2 оказываются статистически незначимыми, то можно сделать вывод, что возраст ребенка не оказывает влияния на расходы по его содержанию.

3. Регрессия с одной количественной и двумя качественными переменными.

Техника фиктивных переменных может быть распространена на произвольное число качественных факторов. Рассмотрим ситуацию с двумя качественными переменными.

Пусть Y –заработная плата сотрудников фирмы, x – стаж работы, D1 – наличие высшего образования, D2 – пол сотрудника:

Таким образом, получим следующую модель:

.

Из этой модели выводятся следующие регрессионные модели:

1. Средняя зарплата женщины без высшего образования:

2. Средняя зарплата женщины с высшим образованием:

3. Средняя зарплата у мужчины без высшего образования:

4. Средняя зарплата мужчины с высшим образованием:

Очевидно, что все регрессии отличаются только свободными членами. Дальнейшее определение статистической значимости коэффициентов γ1 и γ2 позволяет убедиться, влияют ли образование и пол сотрудника на его заработную плату.

Исследуется зависимость между заработной платой рабочего за месяц у ($), х ‑ возрастом рабочего (лет) и фиктивной переменной D – пол рабочего.

1. Необходимо построить модель с фиктивной переменной D, которая принимает два значения: 1 ‑ если пол рабочего мужской; 0 ‑ если пол женский.

2. Проверить статистическую значимость коэффициентов. Сделать выводы.

На предприятии используются станки трех фирм (А, В, С). Исследуется надежность станков. При этом учитывается возраст станка (х, мес.) и время безаварийной работы до последней поломки (y, час). Выборка из 40 станков дала результаты, представленные в таблице.