Физический и математический маятник уравнения движения вывод

Математический и физический маятники

Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.

Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.7.3.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая , направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна

Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α

Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения

Момент силы относительно точки О: , и момент инерции:
M = FL .
Момент инерции J в данном случае
Угловое ускорение:

С учетом этих величин имеем:

(7.8)

Его решение
,

где и

(7.9)

Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.

Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.

При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.

Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α

Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения

. Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:

(7.10)

(7.11)

Решение этого уравнения

Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е. или

.
Из этого соотношения определяем

Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.

Вынужденные колебания — колебания, происходящие под воздействием внешних периодических сил.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону: <\displaystyle F(t)=F_<0>\cos \left(\Omega t\right)>

Примеры вынужденных колебаний: колебания мембраны телефона, иглы швейной машины, поршня в цилиндре автомобильного двигателя, рессор автомобиля, движущегося по неровной дороге, океанические приливы под действием Луны и др

Резонанс

РЕЗОНАНС (франц. resonance, от лат. resono — откликаюсь) — частотно-избирательный отклик колебат. системы на периодич. внеш. воздействие, при к-ром происходит резкое возрастание амплитуды стационарных колебаний. Наблюдается при приближении частоты внеш. воздействия к определённым, характерным для данной системы значениям. В линейных колебат. системах число таких резонансных частот соответствует числу степеней свободы и они совпадают с частотами собственных колебаний. В нелинейных колебат. системах, реактивные и диссипативные параметры к-рых зависят от величины стороннего воздействия, Р. может проявляться и как отклик на внеш. силовое воздействие, и как реакция на периодич. изменение параметров. В строгом значении термин «Р.» относится лишь к случаю силового воздействия.

Резонанс в линейных системах с одной степенью свободы. Пример простейшего случая Р. представляют вынужденные колебания, возбуждаемые сторонним источником — гармонической эдс

E₀cospt с амплитудой Е₀ и частотой p — в колебательном контуре (рис. 1, а).

Рис. 1. Колебательные системы с одной степенью свободы: последовательный (а) и параллельный (б) колебательные контуры, математический маятник (в) и упругий осциллятор (г),

Амплитуда x и фаза f вынужденных колебаний заряда [q(t) = xcos(pt +f)] определяются амплитудой и частотой внеш. силы:

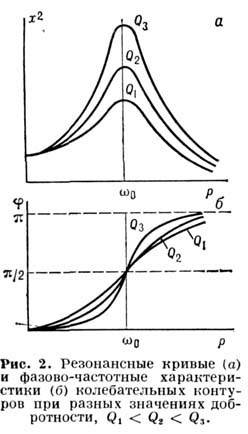
Зависимость амплитуды х стационарных вынужденных колебаний от частоты p вынуждающей силы при постоянной её амплитуде наз. резонансной кривой (рис. 2). В линейном колебат. контуре резонансные кривые, соответствующие различным F, подобны, а фазово-частотная характеристика f(p) не зависит от амплитуды силы.

Вложение энергии в колебат. контур пропорц. первой степени, а диссипация энергии пропорц. квадрату амплитуды колебаний. Это обеспечивает ограничение амплитуд стационарных вынужденных колебаний при Р. Приближение частоты p к собств. частоте w₀сопровождается ростом амплитуды вынужденных колебаний, тем более резким, чем меньше коэф. затухания d. При Р. ток, протекающий через контур, I = 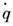= = pxcos(pt + f — p/2), находится в фазе с эдс сторон него источника (f = p/2). Уменьшение амплитуды вынужденных колебаний при неточной настройке обусловлено нарушением синфаз-ности тока и напряжения в цепи.

Важной характеристикой резонансных свойств колебат. системы (осциллятора) является добротностьQ ,к-рая, по определению, равна умноженному на 2p отношению энергии, запасённой в системе, к энергии, рассеиваемой за период колебаний. При воздействии на резонансной частоте амплитуда вынужденных колебаний x в Q раз больше, чем в квазистатич. случае, при 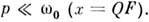Число периодов колебаний, в течение к-рых происходит установление стационарной амплитуды, также пропорц. Q. Наконец, добротность определяет частотную избирательность резонансных систем. Ширина полосы Р. Dw, в пределах к-рой амплитуда вынужденных колебаний спадает в раз от х, обратно пропорц. добротности: Dw = w₀/Q = 2d.

При Р. в электрич. цепях реактивная часть комплексного импеданса обращается в нуль. При этом в после-доват. цепи падения напряжения на катушке индуктивности и на конденсаторе имеют амплитуду QE₀. Однако они складываются в противофазе и взаимно компенсируют друг друга. В параллельной цепи (рис. 1, б)при Р. происходит взаимная компенсация токов в ёмкостной и индуктивной ветвях. В отличие от последоват. Р., при к-ром внеш. силовое воздействие осуществляется источником напряжения, в параллельном контуре резонансные явления реализуются только в том случае, когда внеш. воздействие задаётся источником тока. Соответственно Р. в последоват. контуре называют Р. напряжений, а в параллельном контуре — Р. токов. Если в параллельный контур вместо генератора тока включить генератор напряжения, то на резонансной частоте будут выполняться условия не максимума, а минимума тока, поскольку вследствие компенсации токов в ветвях, содержащих реактивные элементы, проводимость цепи оказывается минимальной (явление антирезонанса).

Подобными чертами обладает явление Р. в механич. и др. колебат. системах. В линейных системах, согласно принципу суперпозиции, реакцию системы на периодич. несинусоидальное воздействие можно найти как сумму откликов на каждую из гармонич. компонент воздействия. Если период несинусоидальной силы равен Т, то резонансное возрастание колебаний может происходить не только при условии w₀ ! 2p/Т, но в зависимости от формы E(t)и при условиях w₀ ! 2pn/T, где n = 1, 2. (Р. на гармониках).

Резонансные кривые определяют, наблюдая изменение амплитуды вынужденных колебаний либо при медленной перестройке частоты p вынуждающей силы, либо при медленном изменении собств. частоты w₀. При высокой добротности осциллятора (Q 1) оба способа дают практически одинаковые результаты. Частотные характеристики, полученные при конечной скорости изменения частоты, отличаются от статич. резонансных кривых, соответствующих бесконечно медленной перестройке: на динамич. частотных характеристиках наблюдается смещение максимума в направлении перестройки частоты, пропорц. m, где — время релаксации колебаний в контуре,

Рис. 3. Статические и динамические амплитудно-частотные характеристики резонанса при различных скоростях нарастания частоты: p(t)= w₀ + t/m, m = 0(1), 0,0625 (г), 0,25(3), 0,695 (4).

t* — время, в течение к-pогo частота p находится в пределах полосы резонанса Dw. При быстрой перестройке частоты, по мере роста m, происходит уменьшение высоты и расширение резонансных кривых, причём их форма становится более асимметричной (рис. 3).

Резонанс в линейных колебательных системах с несколькими степенями свободы. Колебат. системы с неск. степенями свободы представляют собой совокупность взаимодействующих осцилляторов. Примером может служить пара колебат. контуров, связанных за счёт взаимной индукции (рис. 4). Вынужденные колебания в такой системе описываются ур-ниями

Индуктивная связь приводит к тому, что колебания в отд. контурах не могут происходить независимо друг от друга. Однако для любой колебат. системы с неск. степенями свободы можно найти нормальные координаты, к-рые являются линейными комбинациями независимых переменных. Для нормальных координат система ур-ний, подобная (2), преобразуется в цепочку ур-ний для вынужденных колебаний такого же вида, как для одиночных колебат. контуров, с тем отличием, что воздействие на каждую из нормальных координат оказывают силы, приложенные, вообще говоря, в разных частях совокупной колебат. системы. При рассмотрении законов движения в нормальных координатах справедливы все закономерности Р. в системах с одной степенью свободы.

Рис. 4. Колебательная система с двумя степенями свободы — пара контуров со связью за счёт взаимоиндукции.

Резонансное нарастание колебаний происходит во всех частях колебат. системы на одних и тех же частотах (рис. 5), равных частотам собств. колебаний системы. Нормальные частоты не совпадают с парциальными, т. е. с собств. частотами осцилляторов, входящих в совокупную систему. Если частота сторонней силы равна одной из парциальных частот, то в совокупной системе Р. не наступает. Напротив, в этом случае амплитуды вынужденных колебаний достигают минимума, аналогично случаю антирезонанса в системе с одной степенью свободы. Возможность подавления колебаний, частота к-рых равна одной из парциальных, используется в электрич. фильтрах и успокоителях механич. колебаний.

В системе, состоящей из слабо связанных осцилляторов с одинаковыми парциальными частотами, резонансные максимумы, отвечающие близким нормальным частотам, могут сливаться, так что частотная характеристика имеет один максимум (рис. 6). Увеличение связи между осцилляторами приводит к росту интервала между нормальными частотами системы. Изменение формы резонансных кривых при увеличении коэф. связи иллюстрирует рис. 6. Система осцилляторов при связи, близкой к критической, имеет частотную характеристику, уплощённую вблизи Р., причём крутизна её склонов выше, чем у одиночного осциллятора с таким же уровнем потерь. Это свойство обычно используется для создания полосовых электрич. фильтров.

Рис. 6. Резонансные кривые двухконтурной колебательной системы при gQ = 1(1), и 2(3); g = M/L, L₁ = L₂.

Резонанс в распределённых колебательных системах. В распределённых системах (см. Система с распределёнными параметрами)амплитуда и фаза колебаний зависят от пространственных координат. Линейные распределённые колебат. системы характеризуются набором нормальных частот и собств. ф-ций, к-рые описывают пространственное распределение амплитуд собств. колебаний. Резонансные свойства (добротность) распределённых систем определяются не только собств. затуханием, но и связью с окружающей средой, в к-рую происходит излучение части энергии колебаний (электрич., упругих и др.). В распределённых системах, обладающих высокой добротностью (Q 1), вынужденные колебания представляют собой стоячие волны, пространственное распределение амплитуд к-рых является суперпозицией собств. ф-ций (мод), а фаза колебаний одинакова во всех точках. Действие сторонних сил с частотами, близкими к собственным, ведёт к резонансному нарастанию амплитуды вынужденных колебаний во всех точках объёма распределённой резонансной системы (резонатора).

В распределённых системах сохраняют силу все общие свойства Р. Особенностью Р. в распределённых системах (равно как и в системах с неск. степенями свободы) является зависимость амплитуд вынужденных колебаний не только от частоты, но и от пространственного распределения вынуждающей силы. Р. наступает, если пространственное распределение внеш. силы повторяет форму собств. ф-ции, а частота равна соответствующей нормальной частоте. При неблагоприятном пространственном распределении сторонней силы вынужденные колебания не возбуждаются. Это происходит, в частности, тогда, когда сосредоточенная сила прикладывается в точках, для к-рых амплитуда соответствующего нормального колебания обращается в нуль. Так, прикладывая сосредоточенную силу в точке, являющейся узловой для перемещений струны, невозможно возбудить её колебания, поскольку работа силы будет равна нулю. Если распределение сил таково, что работа, совершаемая ими в разл. частях системы, имеет противоположные знаки и в целом не приводит к изменению энергии, вынужденные колебания также не возбуждаются.

Резонанс в нелинейных колебательных системах. В упругих системах нелинейным элементом является пружина, для к-рой связь между деформацией и упругой силой нелинейна, т. е. нарушается закон Гука. В электрич. системах примером нелинейного диссипа-тивного элемента является диод, вольт-амперная характеристика к-рого не подчиняется закону Ома. Нелинейными реактивными (энергоёмкими) элементами являются конденсаторы с сегнетоэлектриком или катушки индуктивности с ферритовыми сердечниками. Параметры этих элементов — ёмкость, индуктивность, сопротивление, а также собств. частоту и коэф. затухания в нелинейных системах можно считать ф-циями тока или напряжения. При этом в нелинейных системах не выполняется суперпозиции принцип.

В нелинейных системах гармонич. сила возбуждает негармонич. колебания, в спектре к-рых имеются кратные частоты, поэтому Р. на гармониках происходит p при синусоидальной внеш. силе. В колебат. системах, обладающих достаточно высокой добротностью и частотной избирательностью, наиб. амплитуду имеет та спектральная компонента, частота к-рой близка к частоте Р. Рассматривая лишь колебания с частотой, близкой к резонансной, можно и в этом случае получить семейство резонансных кривых. Для системы с нелинейными реактивными (энергоёмкими) элементами при r ! w₀ эти кривые изображены на рис. 7. Форма резонансной кривой зависит от амплитуды вынуждающей силы и по мере её увеличения становится всё более асимметричной. Поскольку частота собств. колебаний нелинейного осциллятора зависит от их амплитуды, то и максимумы на резонансных кривых сдвигаются в сторону более высоких или более низких частот. Начиная с нек-рого значения амплитуды силы, резонансные кривые приобретают неоднозначную клювообразную форму. В определённом интервале частот стационарная амплитуда вынужденных колебаний оказывается зависящей от предыстории установления колебаний (явление колебат. гистерезиса). При этом части резонансных кривых, соответствующих неустойчивым состояниям, образуют на плоскости (х, р)область физически нереализуемых режимов (на рис. 7 заштрихована).

Рис. 7. Семейство амплитудно-частотных кривых в случае нелинейного резонанса при различных амплитудах сторонней силы (F₁

Физический и математический маятник уравнения движения вывод

«Физика — 11 класс»

Колебания тела можно описать, используя законы Ньютона.

Уравнение движения тела, колеблющегося под действием силы упругости.

Согласно второму закону Ньютона произведение массы тела на ускорение его равно равнодействующей всех сил, приложенных к телу:

Запишем уравнение движения для шарика, движущегося прямолинейно вдоль горизонтали под действием силы упругости F_упр пружины.
Направим ось ОХ вправо. Пусть начало отсчета координат соответствует положению равновесия шарика.

В проекции на ось ОХ уравнение движения можно записать так:

где а_х и F_{x упр} — проекции ускорения и силы упругости пружины на эту ось.

Согласно закону Гука проекция F_{x ynp} прямо пропорциональна смещению шарика из положения равновесия.
Смещение же равно координате х шарика, причем проекция силы и координата имеют противоположные знаки. Следовательно,

F_{x yпp} = -kх

Разделив левую и правую части уравнения на массу, получим уравнение, описывающее колебания тела под действием силы упругости:

Проекция ускорения тела прямо пропорциональна его координате, взятой с противоположным знаком.

Так как масса и жесткость пружины — постоянные величины, то их отношение также постоянная величина.

Уравнение движения математического маятника

При колебаниях маятника на нерастяжимой нити он все время движется по дуге окружности, радиус которой равен длине нити l.
Положение маятника в любой момент времени определяется одной величиной — углом альфа (α) отклонения нити от вертикали.
Пусть угол α>0, если маятник отклонен вправо от положения равновесия,
и α 0) составляющая силы тяжести F_t направлена влево и ее проекция отрицательна: F_t 0.

Проекция ускорения маятника на касательную к его траектории а_t характеризует быстроту изменения модуля скорости маятника.

Поступая налогично выводу форулы для маятника, колеблющегося под действием силы упругости,
получим уравнение движения для математического маятника (нитяного маятника):

Проекция ускорения тела прямо пропорциональна его координате, взятой с противоположным знаком.

где
l — длина нити маятника,
g — ускорение свободного падения,
х — смещение маятника.

Вывод:

Движение маятника на пружине и колебания маятника на нити происходят одинаковым образом, хотя силы, вызывающие колебания, имеют различную физическую природу.
Ускорение прямо пропорционально координате (смещению от положения равновесия).
Колебания в этих двух случаях совершаются под действием сил, равнодействующая которых прямо пропорциональна смещению колеблющегося тела от положения равновесия и направлена в сторону, противоположную этому смещению.

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Механические колебания. Физика, учебник для 11 класса — Класс!ная физика

1.1. Уравнение гармонических колебаний

В этом разделе мы покажем, что уравнения колебательного движения многих систем, в сущности, одинаковы, так что различные физические процессы могут быть описаны одними и теми же математическими формулами.

Пружинный маятник — это система, состоящая из шарика массой m, подвешенного на пружине длиной .

Рис. 1.2. К выводу уравнения движения для пружинного маятника

В положении равновесия (рис. 1.2) сила тяжести уравновешивается упругой силой :

где – статическое удлинение пружины. Направим ось x вниз и выберем начало отсчета так, что координата x = 0 соответствует положению неподвижного шарика в положении равновесия.

Если теперь оттянуть шарик от положения равновесия на расстояние x, то полное удлинение пружины станет равным . По закону Гука проекция результирующей силы на ось ОХ будет тогда равна

Знак минус означает, что сила стремится уменьшить отклонение от положения равновесия. Полученное выражение соответствует упругой силе слабо деформированной пружины.

Запишем теперь уравнение второго закона Ньютона:

Его можно также представить в виде:

Математический маятник

Математический маятник — это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.

Будем характеризовать отклонение маятника от положения равновесия углом , который образует нить с вертикалью (рис. 1.3).

Рис. 1.3. К выводу уравнения движения математического маятника

При отклонении маятника от положения равновесия на материальную точку массой m действуют сила тяжести и сила натяжения нити . Соответственно, уравнение движения этой материальной точки имеет вид

.

Проецируя его на направления нормали и касательной к траектории (окружности радиуса ), получаем

Модуль скорости равен , учитывая, что при движении точки к положению равновесия угол убывает, а скорость точки растет, напишем

.

Тогда второе из написанных выше уравнений движения приобретает вид

При малых отклонениях маятника от вертикали, когда ,

Физический маятник

Физический маятник — это протяженное колеблющееся тело, закрепленное на оси. Его размеры таковы, что его невозможно рассматривать как материальную точку.

Пример физического маятника приведен на рис. 1.4.

Рис. 1.4. К выводу уравнения движения физического маятника

При отклонении маятника от положения равновесия на угол возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен

где m – масса маятника, а l – расстояние 0C между точкой подвеса 0 и центром масс C маятника.

Рассматривая как вектор, связанный с направлением поворота правилом правого винта, противоположность знаков и можно объяснить тем, что векторы и направлены в противоположные стороны. Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, как I, для маятника можно записать основное уравнение динамики вращательного движения:

Ограничимся рассмотрением малых отклонений от положения равновесия:

В этом случае уравнение колебаний принимает вид:

В случае, когда физический маятник можно представить как материальную точку, колеблющуюся на нити длиной l, момент инерции равен

и мы приходим к уравнению (1.6) движения математического маятника.

Колебания поршня в сосуде с идеальным газом

Рассмотрим цилиндр с площадью поперечного сечения , в который вставлен поршень массы (рис. 1.5). Под поршнем в цилиндре идеальный газ с показателем адиабаты , над поршнем воздух с постоянным (атмосферным) давлением . Поршень может двигаться в цилиндре вверх и вниз без трения. Будем считать, что в равновесии объем идеального газа под поршнем равен и изменения объема газа, обусловленные движением поршня, происходят адиабатно, то есть без теплообмена со стенками цилиндра и поршнем.

Рис. 1.5. Колебания поршня, закрывающего сосуд с идеальным газом

В состоянии равновесия давление в газе под поршнем складывается из атмосферного давления и давления , оказываемого поршнем. Обозначим это результирующее давление :

Переместим поршень на расстояние x вверх. Объем сосуда увеличится и станет равным

Соответственно уменьшится давление. В силу предположения об отсутствии теплообмена, новое давление в газе можно найти из уравнения адиабаты Пуассона

Здесь — показатель адиабаты, зависящий от числа степеней свободы молекул газа.

При малых колебаниях, когда изменение объема газа много меньше его «равновесной» величины , то есть когда

выражение (1.11) можно разложить в ряд Тейлора:

На поршень действуют три силы: сила атмосферного давления , сила давления газа под поршнем и сила тяжести . Знаки сил соответствуют выбору положительного направления оси x вверх. Используя (1.10) и (1.12), находим для равнодействующей этих сил:

Используя (1.13), уравнение движения поршня