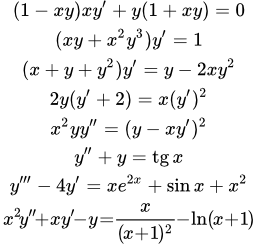Физика дифференциальные уравнения примеры решения

Примеры дифференциальных уравнений с решениями

• Попробуйте решить приведенные ниже дифференциальные уравнения.
• Нажмите на изображение уравнения, и вы попадете на страницу с подробным решением.

Примеры решений дифференциальных уравнений первого порядка

Примеры решений дифференциальных уравнений второго и высших порядков

Найти общее решение дифференциального уравнения, или решение с заданными начальными условиями.

Примеры решений линейных дифференциальных уравнений с постоянными коэффициентами

Примеры решений линейных уравнений в частных производных первого порядка

Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:
,
при .

Найти поверхность, удовлетворяющую данному уравнению
,
и проходящую через данную окружность
, .

Автор: Олег Одинцов . Опубликовано: 28-01-2016 Изменено: 26-11-2021

Физика дифференциальные уравнения примеры решения

Примеры решения задач по механике, требующих интегрирования дифференциальных уравнений

(Задачи взяты из задачника: И.В. Мещерский «Сборник задач по теоретической механике», М.: Наука, 1981г., 460с.)

Задача №1. Пример задачи, приводящей к интегрированию дифференциальных уравнений методом разделения переменных.

При движении тела в неоднородной среде сила сопротивления изменяется по закону Н, где v – скорость тела в м/с, а s – пройденный путь в метрах. Определить пройденный путь как функцию времени, если начальная скорость v ₀=5 м/с.

Будем считать, что движение происходит вдоль оси 0Х, и что при t =0 тело находилось в начале координат, тогда проекция на ось 0Х силы, действующей на тело, может быть записана в виде

.

С учётом этого выражения, имеем следующее уравнение движения (считая массу тела m =1 кг)

, (1)

которое дополняется начальными условиями

, (2)

Решение уравнения второго порядка (1) можно свести к двум последовательным интегрированиям дифференциальных уравнений первого порядка. Чтобы получить первое уравнение, перепишем (1) в виде:

, (3)

и домножим на dt левую и правую части (3), учитывая при этом, что dx = v_xdt , получим:

, или (4)

Это уравнение с разделяющимися переменными (вида (1.5) из Раздела №1 Части I ). Очевидно, что оно, дополняется начальным условием, следующим из (2):

(5)

Разделив переменные в (4), в соответствие с формулой (1.7):

,

вычисляя данные интегралы, получим частный интеграл уравнения (4) (в форме (В.4) из Введения к Части I ):

(6)

Выразив отсюда v_x , будем иметь частное решение уравнения (4) (в форме (В.6) из Введения к Части I ):

(7)

Заменяя теперь в (7)

,

мы снова получаем уравнение с разделяющимися переменными (вида (1.1) из Раздела №1 Части I )

(8)

Разделяя в (8) переменные, с учётом начального условия (2), ищем частный интеграл этого уравнения (в виде (1.4) из Раздела №1 Части I ):

(9)

Вычисляя интегралы в (9), получим:

(10)

— частный интеграл уравнения (8) в форме (В.4) из Введения к Части I. Выражая отсюда x , получим частное решение уравнения (8):

, (11)

которое одновременно является и частным решением уравнения движения (1), удовлетворяющим начальным условиям (2), то есть, представляет собой закон движения тела (координата x , (или в данном случае путь), как функция времени). Таким образом, решение исходного уравнения движения второго порядка (1) в процессе решения задачи было сведено к интегрированию двух уравнений первого порядка с разделяющимися переменными (4) и (8).

Задача №2. Пример задачи, приводящей к интегрированию линейного обыкновенного дифференциального уравнения первого порядка.

Тело К, размерами которого можно пренебречь, установлено в верхней точке А шероховатой поверхности неподвижного полуцилиндра радиуса R . Какую начальную горизонтальную скорость , направленную по касательной к цилиндру, нужно сообщить телу К, чтобы оно начав движение, остановилось на поверхности цилиндра, если коэффициенты трения скольжения при движении и покое одинаковы и равны .

Расставляем силы, действующие на тело, и записываем второй закон Ньютона:

Спроектируем данное равенство на направление движения и перпендикулярное ему. Эти направления указаны на рисунке векторами и . Таким образом, для описания движения мы используем естественный способ. В результате получим:

(1)

Здесь учтено, что центростремительное ускорение

,

.

Сделаем в первом уравнении в (1) замену переменной — перейдем от дифференцирования по времени к дифференцированию по углу :

(т.к. )

С учетом этой замены перепишем (1):

(2)

Домножая второе уравнение на , и вычитая из первого, получим:

(3)

Это уравнение типа (2.1) (из Раздела №2 Части I ), в котором независимой переменной вместо t является ; неизвестной функцией вместо ;

; .

Уравнение (3) дополняется начальным условием:

(4)

С учетом указанных обозначений, используя формулу (2.9) (из Раздела №2 Части I ), решение уравнения (3) можно записать в виде:

(5)

Вычисляя с помощью интегрирования по частям интервалы в (5) , окончательно получим:

(6)

По условиям задачи тело должно остановиться на поверхности; т.е. при каком-то угле .

Подставляя вместо в (6) выразим оттуда :

(7)

Значение угла можно выразить через , поскольку ;

то из уравнений (2) получим:

(8)

Отсюда: ;

(9)

;

из (7) будем иметь:

(10)

Следовательно, чтобы тело остановилось на шероховатой поверхности цилиндра, нужно, чтобы его начальная скорость не превосходила значение, определенного в (10).

Задача №3. Пример задачи, приводящей к решению линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами.

Тело массы 5 кг подвешено к концу пружины жёсткости 20 Н/м и помещено в вязкую среду. Период его колебаний в этом случае равен 10 с. Найти постоянную демпфирования, логарифмический декремент колебаний и период свободных колебаний.

Выберем начало координат в положении статического равновесия тела и расставим силы, действующие на тело в процессе колебаний (считаем, что тело в данный момент времени движется вверх). Если АВ обозначает длину нерастянутой пружины, то отрезок ОВ представляет статическое удлинение пружины под действием силы mg . По закону Гука mg = k × ОВ, где k — коэффициент жёсткости пружины. Записываем второй закон Ньютона:

.

Проектируем это равенство на ось ОХ, учитывая, что

, .

В результате получим уравнение колебаний

, или (1)

где , .

Уравнение (1) представляет собой однородное обыкновенное дифференциальное уравнение второго порядка с постоянными коэффициентами (уравнение (1.1) Части II ). Для его решения используем схему, описанную в Разделе №1 Части II .

Составляем характеристическое уравнение:

. (2)

Вычисляем дискриминант уравнения (2):

. (3)

Поскольку в данном случае, в соответствие с условиями задачи движение тела носит колебательный (периодический) характер, то его координата должна изменяться со временем по гармоническому закону, то есть по закону косинуса или синуса. Для того же, чтобы решение уравнения (1) выражалось через данные функции, мы должны считать, что D (4)

где величины и определяются следующим образом:

, (5)

В случае отсутствия затухания (когда n =0), , и тело совершает свободные колебания с периодом с.

Если же n ¹ 0, то период колебаний, с учётом (5),:

.

Выражаем отсюда , и определяем постоянную демпфирования a (коэффициент пропорциональности в формуле для силы сопротивления):

Подставляя данные задачи, получим a =19 .

В соответствие со своим определением, логарифмический декремент затухания есть натуральный логарифм отношения двух последовательных амплитуд, (то есть взятых через половину периода колебания ): . Вычисляя n и подставляя значение Т, получим =9,5.

Задача №4. Пример задачи, приводящей к решению линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.

Для уменьшения действия на тело массы m возмущающей силы устанавливают пружинный амортизатор с жидкостным демпфером. Коэффициент жёсткости пружины k . Считая, что сила сопротивления пропорциональна первой степени скорости ( ), найти максимальное динамическое давление всей системы на фундамент при установившихся колебаниях.

Направим ось 0 X вдоль направления движения, выбрав начало координат в положении статического равновесия тела. При этом считаем, что сила тяжести скомпенсирована силой статического сжатия пружины амортизатора. Записываем второй закон Ньютона:

.

Проектируем это равенство на ось ОХ, учитывая, что

, , .

В результате получим уравнение колебаний

, или , (1)

где обозначено , .

При колебаниях на фундамент действует сила, складывающаяся из силы деформации пружины и силы сопротивления, равная в соответствие с третьим законом Ньютона,

. (2)

Следовательно, для вычисления этой силы нужно знать уравнение движения тела , для чего необходимо решить уравнение (1). Поскольку в задаче рассматриваются уже установившиеся колебания, то есть рассматривается движение тела, установившееся по истечению достаточно большого промежутка времени от момента его начала. При этом тело будет совершать колебания с частотой вынуждающей силы. Поэтому мы должны найти частное решение уравнения (1), соответствующее этим вынужденным колебаниям. Для этого используем метод подбора по правой части. Представим, в соответствие с формулой (2.5) (из Раздела №2 Части II ) решение уравнения (1) в виде

(3)

Обозначим для краткости записи через и подставим (3) в (1):

Приравнивая коэффициенты при и , получим следующую систему уравнений:

Решая данную систему, находим

, (4)

Подставим (4) в (3):

(5)

Данную формулу, обозначая

, (6)

можно переписать в виде:

(7)

Подставим теперь (7) в (2):

(8)

, (9)

формулу (8) можно переписать в виде

(10)

Отсюда следует, что максимальное динамическое давление всей системы на фундамент равно

. (11)

Примеры решения дифференциальных уравнений с ответами

Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения дифференциальных уравнений

Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x , как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х) , с помощью которой можно обратить уравнение в равенство.

Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.

Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.

Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).

Примеры решения дифференциальных уравнений

Задание

Решить дифференциальное уравнение xy’=y.

Решение

В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь

переписываем дифференциальное уравнение, получаем

Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем

Далее интегрируем полученное уравнение:

В данном случае интегралы берём из таблицы:

После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.

– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const

Ответ

Задание

Найти частное решение дифференциального уравнения

Решение

Действуем по тому же алгоритму, что и в предыдущем решении.

Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:

Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:

Если – это константа, то

0\]» title=»Rendered by QuickLaTeX.com» />

– тоже некоторая константа, заменим её буквой С:

– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.

Получаем общее решение:

Ответ

Задание

Решить дифференциальное уравнение

Решение

В первую очередь необходимо переписать производную в необходимом виде:

Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:

После разделения переменных, интегрируем уравнение, как в примерах выше.

Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:

В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.

Далее упрощаем общий интеграл:

Приводим полученный общий интеграл к виду: F(x,y)=C:

Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(0)=ln2.

Решение

Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.

Начинаем разделять переменные и интегрировать уравнение:

Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.

Получаем общее решение:

Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Задание

Решить дифференциальное уравнение

Решение

При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:

В данном случае константу C считается не обязательным определять под логарифм.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(1)=e. Выполнить проверку.

Решение

Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:

Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:

можно выразить функцию в явном виде.

Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Проверка

Необходимо проверить, выполняется ли начальное условие:

Из равенства выше видно, что начальное условие y(1)=e выполнено.

Далее проводим следующую проверку: удовлетворяет ли вообще частное решение

дифференциальному уравнению. Для этого находим производную:

Подставим полученное частное решение

и найденную производную в исходное уравнение

Получено верное равенство, значит, решение найдено правильно.

Задание

Найти общий интеграл уравнения

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Ответ

Задание

Найти частное решение ДУ.

Решение

Данное ДУ допускает разделение переменных. Разделяем переменные:

Найдем частное решение (частный интеграл), соответствующий заданному начальному условию

Подставляем в общее решение

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Левую часть интегрируем по частям:

В интеграле правой части проведем замену:

(здесь дробь раскладывается методом неопределенных коэффициентов)

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных.

Разделяем переменные и интегрируем:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей: