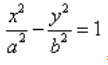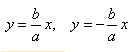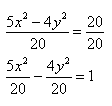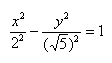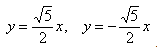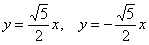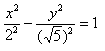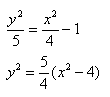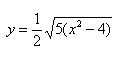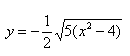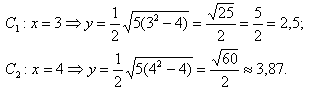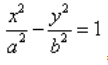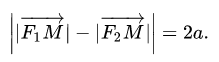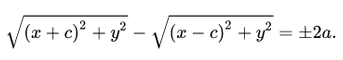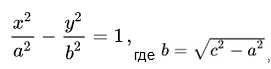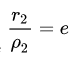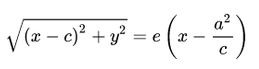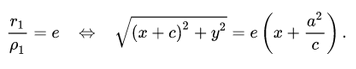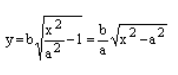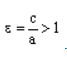Форма гиперболы по ее каноническому уравнению

ГЛАВА 3. КРИВЫЕ ВТОРОГО ПОРЯДКА

Определение. Пусть на плоскости заданы две точки F1 И F2, расстояние между которыми равно 2C. Пусть, кроме того, задано положительное число A, меньшее C. Гиперболой называется множество точек той же плоскости, для каждой из которых модуль разности расстояний до точек F1 и F2, называемых Фокусами гиперболы, есть число постоянное, равное 2А.

Вывод канонического уравнения

Для вывода уравнения гиперболы, которое мы впоследствии назовём каноническим, выберем на плоскости ортонормированную систему координат следующим образом: ось проведем через фокусы гиперболы, а ось — перпендикулярно ей через середину отрезка F1F2 (рис. 1). Согласно определению, гиперболе удовлетворяют те, и только те точки М плоскости, для которых

. (1)

Чтобы получить уравнение гиперболы остаётся только записать равенство (1) в координатах. В выбранной системе координат фокусы гиперболы имеют следующие координаты: F1 (–C; 0); F2 (C; 0). Координаты произвольной (или текущей) точки множества всегда обозначаются X и Y. Таким образом, M(X; Y). Так как

, ,

То уравнение (1) равносильно следующему:

, (2)

Которое, в свою очередь, равносильно уравнению:

. (3)

Оба эти уравнения являются уравнениями гиперболы, но они имеют громоздкий вид, неудобны для использования и для запоминания, поэтому мы попытаемся их преобразовать к более простому виду. Для этого проведем следующую цепочку преобразований:

(3)

.

Учитывая, что , разделив последнее уравнение на , получаем:

. (4′)

Так как , то , поэтому найдется такое положительное число , что . Теперь уравнение (4′) примет вид:

. (4)

Мы доказали, что если точка принадлежит гиперболе, то её координаты удовлетворяют уравнению (3) или (4).

Докажем обратное: если координаты точки удовлетворяют уравнению (4) или (3), то она принадлежит гиперболе.

<M (X; Y) удовлетворяет (4)>

. (5)

. (6)

Находим разность расстояний:

[(4) ]=

=.

Таким образом, (4) – уравнение гиперболы, которое и называется её Каноническим уравнением.

Исследование формы гиперболы по её каноническому уравнению

1. Симметрия. Так как координаты X И Y В уравнение (4) входят только в чётных степенях, то

<M1(X0; Y0) Г> <M2(–X0; Y0) Г, M3(–X0; –Y0) Г; M4(X0; –Y0)Г>.

Это означает, что гипербола (4) симметрична относительно координатных осей и начала координат. Оси симметрии гиперболы называются Осями гиперболы, центр симметрии – её Центром.

2. Пересечение с осями. Если Y = 0, то (4) <X = ±A>. Значит, гипербола пересекает ось в точках A1 (–A; 0) и A2 = (A; 0), которые называются Вершинами гиперболы. Если же X = 0, то (4) решений не имеет, т. е. ось гипербола не пересекает. Та ось гиперболы, которую она пересекает, называется её Действительной осью, а та, которую не пересекает – Мнимой. Числа A и B называются Полуосями гиперболы, действительной и мнимой соответственно.

3. В силу симметрии гиперболы её достаточно нарисовать в первой координатной четверти, а затем продолжить рисунок по симметрии. Если , , то из (4) можно выразить Y:

. (7)

Если X = A, то Y = 0, если же , то и . Вычислим производную:

.

Если , то , поэтому гипербола в вершине имеет вертикальную касательную.

4. Асимптотами гиперболы (4) называются прямые . Рассмотрим ту из них, которая проходит в первой четверти:

. (8)

Сравнивая (7) и (8), видим, что , значит, гипербола расположена ниже своей асимптоты. Кроме того, ели М – точка гиперболы, Р – точка её асимптоты с такой же первой координатой, — расстояние от М до гиперболы (рис.2), то

.

Следовательно, при неограниченном удалении от начала координат гипербола бесконечно близко приближается к своей асимптоте, не пересекая её.

Теперь можно приступить к рисованию. По обе стороны от начала координат откладываем на действительной оси действительные полуоси, а на мнимой – мнимые. Рисуем прямоугольник, стороны которого проходят через полученные точки параллельно осям координат. Точки пересечения прямоугольника с действительной осью – это вершины гиперболы. Затем проводим диагонали прямоугольника и продляем их – это асимптоты гиперболы. Рисуем гиперболу сначала в первой четверти, начиная от вершины и неограниченно приближая её к асимптоте, а затем продолжаем по симметрии в остальные координатные четверти (рис. 3).

В заключение параграфа отметим, что уравнение задаёт гиперболу, действительной осью которой является ось , а школьное уравнение при — это уравнение гиперболы с перпендикулярными асимптотами, составленное относительно её асимптот.

Определение. Пусть на плоскости заданы две точки F1 И F2, расстояние между которыми равно 2C. Пусть, кроме того, задано число A, большее C. Эллипсом называется множество точек той же плоскости, для каждой из которых сумма расстояний до точек F1 и F2, называемых Фокусами эллипса, есть число постоянное, равное 2А.

Упражнение. По аналогии с выводом канонического уравнения гиперболы получите каноническое уравнение эллипса

, (1)

Где (не забывайте про обратную часть!).

Исследование формы эллипса по его каноническому уравнению

1. Из (1) вытекает, что если точка M(X; Y) принадлежит эллипсу, то , т. е. эллипс полностью лежит внутри этого прямоугольника.

2. Так же как и гипербола, эллипс симметричен относительно обеих координатных осей и относительно начала координат. Оси симметрии эллипса называются Осями эллипса, центр симметрии – его Центром.

3. Если Y = 0, то из (1) следует, что X = ±A, если же X = 0, то Y = ±B. Таким образом, эллипс пересекает обе координатные оси: ось в точках A1(–A; 0), A2(A; 0) (они называются вершинами эллипса), а ось — в точках B1(0; –B), B2(0; B). Числа А и B называются полуосями эллипса, большей и меньшей соответственно.

4. В силу симметрии эллипса его также можно вначале нарисовать только в первой четверти, а затем продолжить по симметрии. Если , то из (1) получаем: . Найдем производную:

.

при , поэтому

Функция убывает на отрезке

Рис. 1. . Так как и , то в точке пересечения эллипса с осью он имеет горизонтальную касательную, а в вершине – вертикальную. Так же, как и у гиперболы, фокусы эллипса находятся в точках F1 (–C; 0) F2 (C; 0). Теперь уже можно эллипс изобразить (см. рис. 1).

Замечание. Уравнение (1) задаёт эллипс, фокусы которого лежат на оси абсцисс при , и лежат на оси ординат при . Если же , то (1) – уравнение окружности радиуса с центром в начале координат. В этом случае C = 0. Таким образом, окружность — это частный случай эллипса с совпадающими фокусами.

Параметрические уравнения эллипса

Пусть задан эллипс своим каноническим уравнением

(1), где . Построим две окружности радиусами и Соответственно с центрами в начале координат. Из начала координат проведем луч под углом к положительному направлению оси , и обозначим А и В точки его пересечения соответственно с большей и меньшей окружностями. Через точку А

Рис. 2. проведём вертикальную прямую, через В – горизонтальную, их пересечение обозначим М. Кроме того, обозначим K и N Основания перпендикуляров, опущенных на ось соответственно из точек А и В (рис.2).

Если точка M имеет координаты (X; Y), то по рис. 2 видно, что

,.

Координаты точки M удовлетворяет (1), значит, она принадлежит эллипсу. Очевидно, если изменяется в пределах от 0 до 2, то мы получим все точки эллипса. Отсюда вытекает один из способов построения точек эллипса. Кроме того, мы вывели его параметрические уравнения:

.

Определение. Пусть на плоскости заданы прямая D и точка F на расстоянии P от неё. Параболой называется множество всех точек той же плоскости, для каждой из которых расстояние до точки F, называемой Фокусом параболы, равно расстоянию до прямой D, называемой её Директрисой.

Вывод канонического уравнения

Выберем на плоскости ортонормированную систему координат следующим образом: ось направим через фокус перпендикулярно директрисе в направлении от неё, ось проведем посредине между фокусом и директрисой параллельно последней. Если — произвольная точка параболы, то определение параболы формально запишется в виде равенства ,

. (1)

С учётом того, что в выбранной системе координат , , , получаем:

(1)

Отсюда и вытекает уравнение параболы

, (2)

Называемое каноническим, а число P в этом уравнении (расстояние от фокуса до директрисы) носит название фокального параметра. Парабола с уравнением (2) отличается от школьной только тем, что в ней переменные и поменялись ролями. Поэтому мы не будем подробно останавливаться на исследовании её формы, а как она выглядит, посмотрите на рис. 2.

§ 4. Эксцентриситет и директрисы эллипса и гиперболы

Определения. Эксцентриситетом гиперболы Называется число e, равное отношению половины расстояния между фокусами гиперболы к её действительной полуоси.

Эксцентриситетом эллипса называется число e, равное отношению половины расстояния между фокусами эллипса к его большей полуоси.

Директрисами гиперболы (эллипса) Называются прямые, перпендикулярные её действительной (большей) оси и отстоящие от центра на расстоянии, равном отношению действительной (большей) полуоси к эксцентриситету.

, (1)

, (1I)

, A > B (2)

, A 1 (e );

3. Если содержит первую степень, то только одной переменной, и тогда свободный член равен нулю ( => );

4. Если свободный член не равен нулю, то он равен 1 или -1.

Кривой второго порядка называется множество точек плоскости, удовлетворяющих какому-либо уравнению 2-й степени.

Теорема. Для любой кривой второго 2-го порядка на плоскости существует ортонормированная система координат, в которой эта кривая задаётся каноническим уравнением.

Эту теорему мы докажем позже, в разделе «Линейная алгебра», а сейчас на основании её мы перечислим всевозможные типы кривых второго порядка. Итак, получаем классификацию кривых второго порядка:

Каноническое уравнение гиперболы

Вы будете перенаправлены на Автор24

Каноническое уравнение гиперболы имеет следующий вид: $\frac — \frac = 1$, где $a, b$ — положительные действительные числа.

Для того чтобы составить каноническое уравнение гиперболы, нужно привести квадратное уравнение к каноническому виду.

Вывод канонического уравнения гиперболы

Рисунок 1. Рис. 1.Вывод канонического уравнения гиперболы

Рассмотрим гиперболу с фокусами $F_1$ и $F_2$, находящимися на оси $OX$, причём точка $O$ лежит в центе между фокусами.

Следовательно координаты $F_1(-c; 0)$, а $F_2(c; 0)$, где $c$ — расстояние до фокуса гиперболы.

Рассмотрим произвольную точку $M$, принадлежащую гиперболе.

Отрезки $r_1 =|F_1M|$ и $r_2 =|F_2M|$ называются фокальными радиусами точки $M$ гиперболы.

Из определения гиперболы следует, что $|r_1 -r_2| =2a$, следовательно $r_1 – r_2=±2a$, причём $r_1 = \sqrt<(x + c)^2 + y^2>$, а $r_2 = \sqrt<(x - c)^2 + y^2>$.

Соответственно, уравнение $r_1 – r_2=±2a$ иначе можно записать как $\sqrt <(x + c)^2 + y^2>— \sqrt <(x - c)^2 + y^2>= ±2a$ (1).

Умножим выражение (1) на $\frac <$\sqrt<(x + c)^2 + y^2>+ \sqrt<(x - c)^2 + y^2>><±2a>$, получается:, получается:

Сложим уравнения (1) и (2), получим:

Возведём (3) в квадрат:

$\frac + 2xc + a^2 = (x^2 +2x c + c^2 + y^2)$

$\frac \cdot x^2 – y^2 = c^2 – a^2$

Пусть $b^2 = c^2 – a^2$, так как $c > 0$ и, следовательно $\fracx^2 – y^2 = b^2$

Готовые работы на аналогичную тему

Получаем уравнение: $\frac — \frac = 1$ (4), являющееся каноническим уравнением гиперболы с центром в начале координат.

Каноническое уравнение параболы и гиперболы немного похожи между собой.

Уравнение параболы выглядит следующим образом:

$y^2 = px$, где число $p$ должно быть больше нуля; это число называется фокальным параметром.

Каноническое уравнение гиперболы примеры решения

Ниже небольшая инструкция о том, как найти каноническое уравнение гиперболы.

Приведём уравнение $5x^2 — 4y^2 = 20$ к каноническому виду гиперболического уравнения, для этого разделим всё уравнение на $20$:

Запишем знаменатели в виде степеней:

Теперь вы знаете, как написать каноническое уравнение гиперболы. Дальше мы расскажем о том, как строить гиперболу по каноническому уравнению.

Построение гиперболы по каноническому уравнению

Теперь давайте рассмотрим, как построить гиперболу по каноническому уравнению.

Рисунок 2. Рис. 2. Построение гиперболы по каноническому уравнению

Для начала необходимо построить асимптоты для данной гиперболы, их формулы определяются из уравнения $y = ±\frac$. Для нашего канонического уравнения гиперболы они будут выглядеть так: $y = ±\frac<\sqrt<5>> <2>\cdot x$

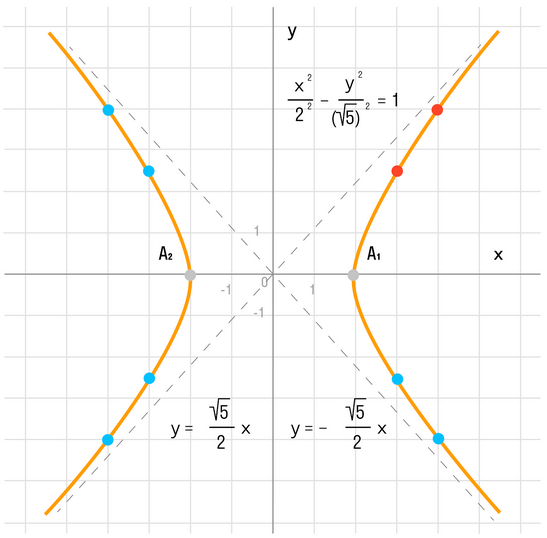
Теперь найдём вершины гиперболы, они расположены на оси абсисс в точках $(0; a)$ и $(0; -a)$, назовём их точками $A_1, A_2$. Вершины нашей гиперболы находятся в точках $(2; 0)$ и $(-2; 0)$.

Далее необходимо найти две-три точки, принадлежащие любой из двух ветвей гиперболы, если гипербола без смещения – точки на второй ветви будут симметричны им относительно осей гиперболы. Выразим $y$ из канонического уравнения нашей гиперболы:

Найдём точки для положительной части гиперболы:

при $x = 3, y =2.5$, а при $x = 3, y ≈3,87$.

Теперь можно отложить все эти точки и построить график гиперболы.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 30 11 2021

Что такое гипербола

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие гиперболы

Гипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (они же — «фокусы») — величина постоянная и меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы в алгебре выглядит так:

, где a и b — положительные действительные числа.

Кстати, канонический значит принятый за образец.

В отличие от эллипса, здесь не соблюдается условие a > b, значит а может быть меньше b. А если a = b, то гипербола будет равносторонней.

Мы помним, что гипербола в математике выглядит так y = 1/x, что значительно отличается от канонической записи.

Вспомним особенности математической гиперболы:

• Две симметричные ветви.
• Две асимптоты. Асимптота — это прямая, которая обладает таким свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность. Их значение помогает найти специальное уравнение асимптот гиперболы.

Если гипербола задана каноническим уравнением, то асимптоты можно найти так:

Пример 1. Построить гиперболу, которая задана уравнением 5(x^2) — 4(y^2) = 20.

Приведем данное уравнение к каноническому виду (x^2)/(a^2) — (y^2)/(b^2) = 1.

Чтобы получить «единицу» в правой части, обе части исходного уравнения делим на 20:

Сокращаем обе дроби в уме или при помощи трехэтажной дроби:

Выделяем квадраты в знаменателях:

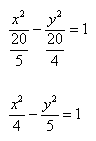
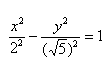
Можно было сделать проще и дроби левой части 5(x^2)/20 — 4(y^2)/20 = 1 сразу сократить и получить (x^2)/4 — (y^2)/5 = 1. Нам повезло с примером, потому что число 20 делится и на 4 и на 5. Рассмотрим пример посложнее.

Пример 2. Построить гиперболу, которая задана уравнением 3(x^2)/20 — 8(y^2)/20 = 1.

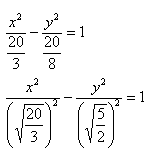
1. Произведем сокращение при помощи трехэтажной дроби:
2. Воспользуемся каноническим уравнением
   
   • Найдем асимптоты гиперболы. Вот так:
     Важно! Без этого шага ветви гиперболы «вылезут» за асимптоты.
   • Найдем две вершины гиперболы, которые расположены на оси абсцисс в точках A1(a; 0), A2(-a; 0).

Если y = 0, то каноническое уравнение (x^2)/(a^2) — (y^2)/(b^2) = 1 превращается в (x^2)/(a^2) = 1, из чего следует, что x^2 = a^2 -> x = a, x = -a.

Данная гипербола имеет вершины A1(2; 0), A2(-2; 0).

Найдем дополнительные точки — хватит двух-трех.

В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для одной координатной четверти.

Способ такой же, как при построении эллипса. Из полученного канонического уравнения

на черновике выражаем:

Уравнение распадается на две функции:

— определяет верхние дуги гиперболы (то, что ищем);

— определяет нижние дуги гиперболы.

Далее найдем точки с абсциссами x = 3, x = 4:

Может возникнуть техническая трудность с иррациональным угловым коэффициентом √5/2 ≈ 1,12, но это вполне преодолимая проблема.

Действительная ось гиперболы — отрезок А1А2.

Расстояние между вершинами — длина |A1A2| = 2a.

Действительная полуось гиперболы — число a = |OA1| = |OA2|.

Мнимая полуось гиперболы — число b.

В нашем примере: а = 2, b = √5, |А1А2| = 4. И если такую гиперболу повернуть вокруг центра симметрии или переместить, то значения не изменятся.

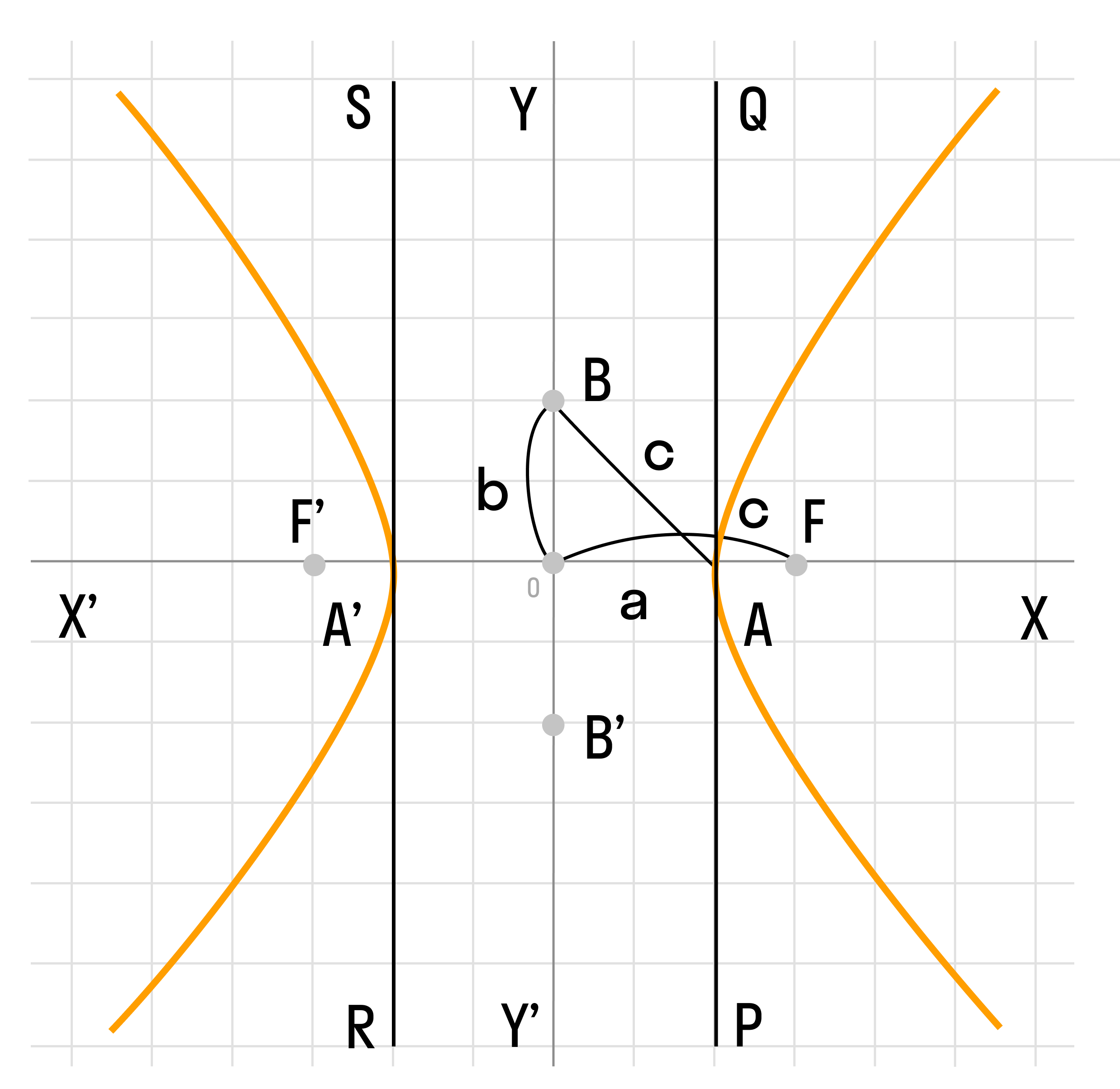
Форма гиперболы

Повторим основные термины и узнаем, какие у гиперболы бывают формы.

Гипербола симметрична относительно точки О — середины отрезка F’F. Она также симметрична относительно прямой F’F и прямой Y’Y, проведенной через О перпендикулярно F’F. Точка О — это центр гиперболы.

Прямая F’F пересекает гиперболу в двух точках: A (a; 0) и A’ (-a; 0). Эти точки — вершины гиперболы. Отрезок А’А = 2a — это действительная ось гиперболы.

Несмотря на то, что прямая Y’Y не пересекает гиперболу, на ней принято откладывать отрезки B’O = OB = b. Такой отрезок B’B = 2b (также и прямую Y’Y) можно назвать мнимой осью гиперболы.

Так как AB^2 = OA^2 + OB^2 = a^2 + b^2, то из равенства следует: AB = c, то есть расстояние от вершины гиперболы до конца мнимой оси равно полуфокусному расстоянию.

Мнимая ось 2b может быть больше, меньше или равна действительной оси 2а. Если действительная и мнимая оси равны (a = b) — это равносторонняя гипербола.

Отношение F’F/А’А фокусного расстояния к действительной оси называется эксцентриситетом гиперболы и обозначается e. Эксцентриситет равносторонней гиперболы равен √2.

Гипербола лежит целиком вне полосы, ограниченной прямыми PQ и RS, параллельными Y’Y и отстоящими от Y’Y на расстояние OA =A’O = a. Вправо и влево от этой полосы гипербола продолжается неограниченно.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Фокальное свойство гиперболы

Точки F1 и F2 называют фокусами гиперболы, расстояние 2c = F1F2 между ними — фокусным расстоянием, середина O отрезка F1F2 — центром гиперболы, число 2а — длиной действительной оси гиперболы (соответственно, а — действительной полуосью гиперболы).

Отрезки F1M и F2M, которые соединяют произвольную точку M гиперболы с ее фокусами, называются фокальными радиусами точки M. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.

Отношение e = a/c, где c = √(a^2 + b^2), называется эксцентриситетом гиперболы. Из определения (2a 1 .

Геометрическое определение гиперболы, которое выражает ее фокальное свойство, аналогично ее аналитическому определению — линии, которая задана каноническим уравнением гиперболы:

Рассмотрим, как это выглядит на прямоугольной системе координат:

• пусть центр O гиперболы будет началом системы координат;
• прямую, которая проходит через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки F1 к точке F2);
• прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат Oxy оказалась правой).

Воспользуемся геометрическим определением и составим уравнение гиперболы, которое выразит фокальное свойство. В выбранной системе координат определяем координаты фокусов F1(-c, 0) и F2(c, 0). Для произвольной точки M(x, y), принадлежащей параболе, имеем:

Запишем это уравнение в координатной форме:

Избавимся от иррациональности и придем к каноническому уравнению гиперболы:

, т.е. выбранная система координат является канонической.

Если рассуждать в обратном порядке, можно убедиться, что все точки, координаты которых удовлетворяют уравнению (x^2)/(a^2) — (y^2)/(b^2) = 1, и только они, принадлежат геометрическому месту точек, называемому гиперболой. Именно поэтому аналитическое определение гиперболы эквивалентно его геометрическому определению.

Директориальное свойство гиперболы

Директрисы гиперболы — это две прямые, которые проходят параллельно оси.

ординат канонической системы координат на одинаковом расстоянии (a^2)/c от нее. Если а = 0, гипербола вырождается в пару пересекающихся прямых, и директрисы совпадают.

Директориальное свойство гиперболы звучит так:

Гиперболу с эксцентриситетом e = 1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки F (фокуса) к расстоянию до заданной прямой d (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету e.

Здесь F и d — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.

На самом деле для фокуса F2 и директрисы d2 условие

можно записать в координатной форме так:

Избавляясь от иррациональности и заменяя e = a/c, c^2 — a^2 = b^2, мы придем к каноническому уравнению гиперболы. Аналогичные рассуждения можно провести для фокуса F1 и директрисы d1:

Построение гиперболы

Чтобы запомнить алгоритм построения гиперболы, рассмотрим чертёж и комментарии к нему.

Построим основной прямоугольник гиперболы и проведем его диагонали. Если продолжим диагонали прямоугольника за его пределы, получим асимптоты гиперболы.

В силу симметрии достаточно построить гиперболу в первой четверти, где она является графиком функции:

Важно учесть, что данная функция возрастает на промежутке [a; ∞], при x = a, y = 0 и ее график приближается снизу к асимптоте y = (b/a) * x. Рисуем график:

Далее построенный в первой четверти график симметрично отображаем относительно оси Ох и получаем правую ветвь гиперболы. Теперь отобразим правую ветвь гиперболы относительно оси Оу.

По определению эксцентриситет гиперболы равен

Зафиксируем действительную ось 2а и начнем изменять фокусное расстояние 2с.

Так как b^2 = c^2 — a^2, то величина b изменится.

При этом ε -> 1, b -> 0 и мнимые вершины B1, B2 стремятся к началу координат, асимптоты приближаются к оси Ох. Основной прямоугольник гиперболы выражается в пределе в отрезок A1A2, а сама гипербола выражается в два луча на оси абсцисс: (-∞; -a] и [a; ∞).

При этом ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаются к прямым x = +-a и в пределе сливаются с ними. Гипербола выражается в две прямые x = +-a, которые параллельны оси Оу.

При этом ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаются к прямым x = +-a и в пределе сливаются с ними. Гипербола выражается в две прямые x = +-a, которые параллельны оси Оу.

Равносторонняя гипербола это такая гипербола, у которой эксцентриситет равен √2. Ее еще называют равнобочной.

Из определения следует, что в равносторонняя гиперболе a = b, поэтому ее каноническое уравнение выглядит так: x^2 — y^2 = a^2

Действительно, ε = c/a = √2, откуда c^2 = 2a^2 и b^2 = c^2 — a^2 = a^2. И так как а и b положительные числа, получаем a = b.