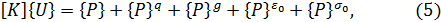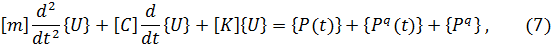Формирование системы разрешающих уравнений метода конечных элементов

Разрешающие уравнение МКЭ

Из условий равновесия узлов или с помощью вариационных принципов, а также методов невязок, применяемых ко всей конечно- элементной модели, составляется общая система уравнений равновесия всей конечно-элементной модели исследуемого деформируемого тела. Для статических задач она имеет вид:

где общая (глобальная) матрица жесткости конечно-элементной модели;

< Р > общий вектор заданных внешних узловых сил;

общие (глобальные) векторы узловых сил, эквивалентных распределенным поверхностным и массовым силам, начальным деформациям, начальным напряжениям.

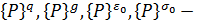
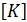
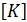
Компоненты матрицы являются коэффициентами жесткости модели. Они вычисляются путем суммирования соответствующих коэффициентов жесткости конечных элементов. Матрица жесткости для конечно-элементной модели обладает симметрией, имеет ленточную структуру и редкое заполнение.

Общий вектор заданных внешних узловых сил <Р>можно пред­ ставить в виде:

где 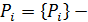подматрица из n₁ компонентов силы, приложенной в узле i. Для трехмерной задачи будем иметь . Как видно из выражения (6), индексация компонентов может быть или по общим номерам степеней свободы модели или по общим номерам узлов с добавлением индекса узловой степени свободы, как у общего вектора узловых перемещений (2).

Общие (глобальные) векторы узловых сил 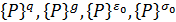собираются из компонентов соответствующих элементных векторов. Их структура такая же, как у вектора .

В динамических задачах на основании принципа Даламбера в уравнения (5) добавляются силы инерции. Так как силы инерции выражаются через ускорения, которые являются вторыми производными от перемещений, то уравнения равновесия (5) превращаются в общие (глобальные) дифференциальные уравнения движения, в которых внешние силы могут быть переменными:

где и общие (глобальные) матрицы масс и демпфирования модели, которые собираются из компонентов соответствующих элементных матриц.

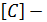
С помощью уравнений (7) выполняются различные виды динамического анализа: модальный анализ, где определяются собственные частоты и формы конструкций; гармонический анализ, где определяется отклик системы на внешнюю периодическую силу с различной частотой; полный анализ динамического процесса, где производится интегрирование дифференциальных уравнений движения.

В статических задачах задаваемые перемещения (связи) должны исключать возможность перемещения нагруженной конструкции как абсолютно твердого тела. Только в этом случае разрешающая система уравнений (5), после учета граничных условий, будет иметь единственное решение. До учета связей исходная система (5) имеет линейно зависимые уравнения, определитель ее матрицы жесткости равен нулю, следовательно, матрица жесткости свободного тела является сингулярной, и нельзя найти однозначного решения для узловых перемещений. [5, 7] Динамические задачи, описываемые уравнениями (7), могут решаться без наложения связей — перемещений.

Решение уравнений МКЭ

Общая система уравнений равновесия (5), полученная методом конечных элементов для статической линейно-упругой модели тела, является, с математической точки зрения, системой линейных алгебраических уравнений (СЛАУ). После учета правильно наложенных связей, не допускающих движения модели как абсолютно твердого тела, определитель матрицы жесткости [К] не равен нулю и, следовательно, существует единственное решение — общий вектор узловых перемещений .

Точность и эффективность различных способов решения СЛАУ (5) во многом зависит от структуры и свойств матрицы [К]: размера, обусловленности, симметричности, заполненности и др. [2]. Известные алгоритмы решения СЛАУ можно разделить в основном на две группы: прямые методы и итерационные методы [1, 2, 5, 6].

Прямые («точные») методы позволяют получать с помощью конечного числа операций точные значения неизвестных, если коэффициенты и правые части уравнений заданы точно и нет округлений при вычислениях. Среди множества прямых методов наибольшее применение имеют: метод исключения неизвестных Гаусса, метод квадратного корня, а также их разновидности, в частности, фронтальный метод и схема разложения Холецкого.

Итерационные методы характеризуются тем, что вначале задаются некоторыми приближенными значениями неизвестных. Затем с помощью каких-либо алгоритмов их последовательно уточняют, приближаясь к точному решению. Наиболее часто используются метод прямой итерации, метод Гаусса-Зейделя, метод последовательной верхней релаксации, градиентные методы наискорейшего спуска и сопряженных градиентов.

Дифференциальные уравнения движения (7) интегрируются различными численными методами [5]. В результате находятся узловые перемещения. Через них определяются все другие искомые величины так же, как функции времени.

Конечно-элементные модели могут быть нелинейными. Модель деформирования физически нелинейна, если в ней учитывается нелинейное поведение материала — нелинейная упругость, текучесть, ползучесть и др. Геометрическая нелинейность при деформировании обусловлена большими деформациями и большими перемещениями.

Нелинейные задачи решаются итерационными методами, при этом на каждой итерации рассматриваются квазилинейные уравнения. В практических вычислениях часто применяется метод Ньютона- Рафсона и его модификации [5]. Для нелинейных задач деформирования иногда эффективны методы переменных параметров упругости, начальных деформаций и начальных напряжений. Если в нелинейной задаче важна история нагружения, нужно производить решение малыми шагами нагрузки.

Метод конечных элементов. решение плоской задачи

Метод конечных элементов. Решение плоской задачи

4.1. Содержание метода.

Метод конечных элементов (MKЭ) представляет собой эффективный численный метод решения инженерных и физических задач. Он широко применяется при проектировании судов, летательных аппаратов, несущих систем многоэтажных зданий и т. п. Для МКЭ характерна ясная физическая трактовка. Его можно рассматривать, в частности, как обобщение классического метода строительной механики — метода перемещений. С другой стороны МКЭ является своеобразной формой часто применяемого вариационного метода Ритца. Различие между традиционной формой метода Ритца и МКЭ состоит в выборе системы координатных функций. Если в методе Ритца функции (обычно ряды) задаются для всей области, то в МКЭ они задаются для ее частей и через множество этих функций определяется состояние системы.

Классический подход к задаче об изучении напряженно-деформированного состояния диска (рис. 4.1) предполагает изучение бесконечно малого его элемента. Получающиеся при этом дифференциальные уравнения в частных производных (равновесия и геометрические) совместно с физическими уравнениями и контурными условиями позволяют определить напряжения, деформации и перемещения в каждой точке диска.

Метод конечных элементов предполагает иной подход. Рассматривается элемент конечных размеров, за счет чего осуществляется переход от сплошной системы с бесконечным числом степеней свободы, к системе с конечным числом степеней свободы.

Разделим воображаемыми линиями диск, изображенный на рис. 4.1, на некоторое количество элементов конечных размеров, например, треугольной формы и примем за узловые точки их вершины. Очевидно, что если диск находится в равновесии то и его элемент, определенный узлами i, j, k, под воздействием напряжений (усилий) от смежных элементов, также уравновешен. Приложим затем к е-му элементу вместо фактических усилий, действующих вдоль его граней статически эквивалентные узловые силы, т. е. силы, вызывающие внутри элемента действительное напряженно-деформированное состояние (рис. 4.2.).

Поставив в соответствие каждому узловому усилию узловое перемещение (рис. 4.2, (б)) представим сплошной диск набором конечных элементов, взаимодействующих между собой в конечном числе узловых точек.

Такой подход позволяет в дальнейшем использовать один из известных классических методов строительной механики, например метод перемещений (возможно также применение метода сил, либо смешанного). Для этого необходимо установить матрицы жесткости всех конечных элементов и, из условия равновесия узлов, получить разрешающие уравнения задачи. Найденные узловые перемещения не дают, однако, полной характеристики напряженно-деформированного состояния диска. Необходим переход от этих величин к перемещениям, напряжениям и деформациям внутри конечных элементов, т. е. речь идет о решении плоской задачи для каждого конечного элемента, находящегося под воздействием узловых перемещений. Такой переход в МКЭ осуществляется приближенно, путем задания интерполяционных (координатных) функций (функций формы), что и делает метод приближенным. Функции эти (обычно полиномы) такие, что обеспечивают неразрывность перемещений при переходе от одного элемента к другому.

Естественно, что при реализации МКЭ возникает необходимость приведения действующих на конструкцию нагрузок к сосредоточенным узловым силам.

Обычно все зависимости, связанные с конечным элементом, строятся в местной системе координат, с последующим переходом в общую систему для всей области. Это позволяет заранее получить необходимые соотношения для часто применяемых типов конечных элементов.

Решение задач по методу конечного элемента содержит следующие этапы:

1. Разбиение заданной области на конечные элементы. Нумерация узлов и элементов.

2. Построение матриц жесткости конечных элементов.

3. Сведение нагрузок и воздействий, приложенных к конечным элементам, к узловым силам.

4. Формирование общей системы уравнений; учет условий закрепления. Решение системы уравнений.

5. Определение напряжений и (при необходимости) деформаций в. конечных элементах.

4.2. Дискретизация области.

Разбиение области на подобласти представляет собой первый шаг на пути к решению задачи, и именно этот шаг не имеет теоретического обоснования. Искусство разбиения области зависит от имеющихся инженерных навыков. Плохое или несовершенное разбиение будет приводить к ошибочным результатам, если даже остальные этапы метода осуществляются с достаточной точностью.

Дискретизация области (тела) включает задание числа, размеров и формы подобластей, которые используются для построения дискретной модели реального тела. При этом, с одной стороны, элементы должны быть выбраны достаточно малыми, чтобы получить приемлемые результаты, а с другой стороны, применение достаточно крупных элементов сокращает вычислительную работу. Нужно иметь некоторые общие соображения об окончательных результатах, с тем, чтобы можно было уменьшить размеры элементов в тех областях, где ожидаемый результат может сильно меняться.

При решении задач методом конечных элементов используются элементы различных типов. Наиболее распространенные типы элементов приведены в табл. 4.1. Ниже будут рассматриваться в основном трехузловые треугольные КЭ, как наиболее простые и чаще других применяемые для решения плоской задачи.