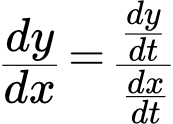Формула дифференцирования функции заданной параметрическими уравнениями

Производная параметрически заданной функции

Функцию можно задать несколькими способами. Это зависит от правила, которое используется при ее задании. Явный вид задания функции имеет вид y = f ( x ) . Бывают случаи, когда ее описание невозможно или неудобно. Если есть множество пар ( х ; у ) ,которые необходимо вычислять для параметра t по промежутку ( а ; b ) . Для решения системы x = 3 · cos t y = 3 · sin t с 0 ≤ t 2 π необходимо задавать окружность с центром координат с радиусом равным 3 .

Определение параметрической функции

Отсюда имеем, что x = φ ( t ) , y = ψ ( t ) определены на при значении t ∈ ( a ; b ) и имеют обратную функцию t = Θ ( x ) для x = φ ( t ) , тогда идет речь о задании параметрического уравнения функции вида y = ψ ( Θ ( x ) ) .

Бывают случаи, когда для исследования функции требуется заниматься поиском производной по х . Рассмотрим формулу производной параметрически заданной функции вида y x ‘ = ψ ‘ ( t ) φ ‘ ( t ) , поговорим о производной 2 и n -ого порядка.

Вывод формулы производной параметрически заданной функции

Имеем, что x = φ ( t ) , y = ψ ( t ) , определенные и дифферецируемые при значении t ∈ a ; b , где x t ‘ = φ ‘ ( t ) ≠ 0 и x = φ ( t ) , тогда существует обратная функция вида t = Θ ( x ) .

Для начала следует переходить от параметрического задания к явному. Для этого нужно получить сложную функцию вида y = ψ ( t ) = ψ ( Θ ( x ) ) , где имеется аргумент x .

Исходя из правила нахождения производной сложной функции, получаем, что y ‘ x = ψ Θ ( x ) = ψ ‘ Θ x · Θ ‘ x .

Отсюда видно, что t = Θ ( x ) и x = φ ( t ) являются обратными функциями из формулы обратной функции Θ ‘ ( x ) = 1 φ ‘ ( t ) , тогда y ‘ x = ψ ‘ Θ ( x ) · Θ ‘ ( x ) = ψ ‘ ( t ) φ ‘ ( t ) .

Перейдем к рассмотрению решения нескольких примеров с использованием таблицы производных по правилу дифференцирования.

Найти производную для функции x = t 2 + 1 y = t .

Решение

По условию имеем, что φ ( t ) = t 2 + 1 , ψ ( t ) = t , отсюда получаем, что φ ‘ ( t ) = t 2 + 1 ‘ , ψ ‘ ( t ) = t ‘ = 1 . Необходимо использовать выведенную формулу и записать ответ в виде:

y ‘ x = ψ ‘ ( t ) φ ‘ ( t ) = 1 2 t

Ответ: y x ‘ = 1 2 t x = t 2 + 1 .

При работе с производной функции ч параметром t указывается выражение аргумента x через этот же параметр t , чтобы не потерять связь между значениями производной и параметрически заданной функции с аргументом, которому и соответствуют эти значения.

Чтобы определить производную второго порядка параметрически заданной функции, нужно использовать формулу производной первого порядка на полученной функции, тогда получаем, что

y » x = ψ ‘ ( t ) φ ‘ ( t ) ‘ φ ‘ ( t ) = ψ » ( t ) · φ ‘ ( t ) — ψ ‘ ( t ) · φ » ( t ) φ ‘ ( t ) 2 φ ‘ ( t ) = ψ » ( t ) · φ ‘ ( t ) — ψ ‘ ( t ) · φ » ( t ) φ ‘ ( t ) 3 .

Найти производные 2 и 2 порядка заданной функции x = cos ( 2 t ) y = t 2 .

Решение

По условию получаем, что φ ( t ) = cos ( 2 t ) , ψ ( t ) = t 2 .

Тогда после преобразования

φ ‘ ( t ) = cos ( 2 t ) ‘ = — sin ( 2 t ) · 2 t ‘ = — 2 sin ( 2 t ) ψ ( t ) = t 2 ‘ = 2 t

Отсюда следует, что y x ‘ = ψ ‘ ( t ) φ ‘ ( t ) = 2 t — 2 sin 2 t = — t sin ( 2 t ) .

Получим, что вид производной 1 порядка x = cos ( 2 t ) y x ‘ = — t sin ( 2 t ) .

Для решения нужно применить формулу производной второго порядка. Получаем выражение вида

y x » = — t sin ( 2 t ) φ ‘ t = — t ‘ · sin ( 2 t ) — t · ( sin ( 2 t ) ) ‘ sin 2 ( 2 t ) — 2 sin ( 2 t ) = = 1 · sin ( 2 t ) — t · cos ( 2 t ) · ( 2 t ) ‘ 2 sin 3 ( 2 t ) = sin ( 2 t ) — 2 t cos ( 2 t ) 2 sin 3 ( 2 t )

Тогда задание производной 2 порядка с помощью параметрической функции

x = cos ( 2 t ) y x » = sin ( 2 t ) — 2 t cos ( 2 t ) 2 sin 3 ( 2 t )

Аналогичное решение возможно решить другим методом. Тогда

φ ‘ t = ( cos ( 2 t ) ) ‘ = — sin ( 2 t ) · 2 t ‘ = — 2 sin ( 2 t ) ⇒ φ » t = — 2 sin ( 2 t ) ‘ = — 2 · sin ( 2 t ) ‘ = — 2 cos ( 2 t ) · ( 2 t ) ‘ = — 4 cos ( 2 t ) ψ ‘ ( t ) = ( t 2 ) ‘ = 2 t ⇒ ψ » ( t ) = ( 2 t ) ‘ = 2

Отсюда получаем, что

y » x = ψ » ( t ) · φ ‘ ( t ) — ψ ‘ ( t ) · φ » ( t ) φ ‘ ( t ) 3 = 2 · — 2 sin ( 2 t ) — 2 t · ( — 4 cos ( 2 t ) ) — 2 sin 2 t 3 = = sin ( 2 t ) — 2 t · cos ( 2 t ) 2 s i n 3 ( 2 t )

Ответ: y » x = sin ( 2 t ) — 2 t · cos ( 2 t ) 2 s i n 3 ( 2 t )

Аналогичным образом производится нахождение производных высших порядков с параметрически заданными функциями.

Производная функции, заданной параметрическим способом

Формула производной

Пусть функция задана параметрическим способом:
(1)
где некоторая переменная, называемая параметром. И пусть функции и имеют производные при некотором значении переменной . Причем и функция имеет обратную функцию в некоторой окрестности точки . Тогда функция (1) имеет в точке производную , которая, в параметрическом виде, определяется по формулам:
(2)

Здесь и – производные функций и по переменной (параметру) . Их часто записывают в следующем виде:
;
.

Тогда систему (2) можно записать так:

Доказательство

По условию, функция имеет обратную функцию. Обозначим ее как
.
Тогда исходную функцию можно представить как сложную функцию:
.
Найдем ее производную, применяя правила дифференцирования сложной и обратной функций:
.

Доказательство вторым способом

Найдем производную вторым способом, исходя из определения производной функции в точке :
.
Введем обозначение:
.
Тогда и предыдущая формула принимает вид:
.

Воспользуемся тем, что функция имеет обратную функцию , в окрестности точки .
Введем обозначения:
; ;
; .
Разделим числитель и знаменатель дроби на :
.
При , . Тогда
.

Производные высших порядков

Чтобы найти производные высших порядков, надо выполнять дифференцирование несколько раз. Допустим, нам надо найти производную второго порядка от функции, заданной параметрическим способом, следующего вида:
(1)

По формуле (2) находим первую производную, которая также определяется параметрическим способом:
(2)

Обозначим первую производную, посредством переменной :
.
Тогда, чтобы найти вторую производную от функции по переменной , нужно найти первую производную от функции по переменной . Зависимость переменной от переменной также задана параметрическим способом:
(3)
Сравнивая (3) с формулами (1) и (2), находим:

Теперь выразим результат через функции и . Для этого подставим и применим формулу производной дроби:
.
Тогда
.

Отсюда получаем вторую производную функции по переменной :

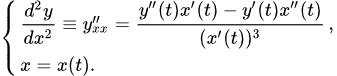
Она также задана в параметрическом виде. Заметим, что первую строку также можно записать следующим образом:
.

Продолжая процесс, можно получить производные функции от переменной третьего и более высоких порядков.

Заметим, что можно не вводить обозначение для производной . Можно записать так:
;
.

Пример 1

Найдите производную от функции, заданной параметрическим способом:

Пример 2

Найдите производную от функции, выраженной через параметр :

Раскроим скобки, применяя формулы для степенных функций и корней:
.

Находим производную . Для этого введем переменную и применим формулу производной сложной функции.

.

Находим искомую производную:
.

Пример 3

Найдите производные второго и третьего порядков от функции, заданной параметрическим способом в примере 1:

В примере 1 мы нашли производную первого порядка:

Введем обозначение . Тогда функция является производной по . Она задана параметрическим способом:

Чтобы найти вторую производную по , нам надо найти первую производную по .

Дифференцируем по .
.
Производную по мы нашли в примере 1:
.
Производная второго порядка по равна производной первого порядка по :
.

Итак, мы нашли производную второго порядка по в параметрическом виде:

Теперь находим производную третьего порядка. Введем обозначение . Тогда нам нужно найти производную первого порядка от функции , которая задана параметрическим способом:

Производная третьего порядка по равна производной первого порядка по :
.

Замечание

Можно не вводить переменные и , которые являются производными и , соответственно. Тогда можно записать так:
;
;
;
;
;
;
;
;
.

В параметрическом представлении, производная второго порядка имеет следующий вид:

Производная третьего порядка:

Автор: Олег Одинцов . Опубликовано: 22-01-2017

Производная функции, заданной параметрически

Сегодня мы научимся считать производную параметрической функции. Для этого разберём основную формулу, несколько примеров, но главное — одну из самых частых и глупых ошибок, которые допускают начинающие студенты.

Начнём с ключевых определений и соображений.

1. Функция, заданная параметрически

Считая производные, мы привыкли работать с функциями, заданными аналитически, т.е. формулой $y=f\left( x \right)$. Подставляя в эту формулу разные значения $x$, мы легко находим значение $y$.

Несколько примеров таких функций:

• Квадратичная функция: $y=<^<2>>$. График — парабола.
• Показательная функция: $y=<<\text>^>$. Она же «экспонента».
• Тригонометрическая функция: $y=\sin x$. График — синусоида.

Но что если величины $y$ и $x$ зависят не друг от друга, а от некой третьей переменной? Скажем, от параметра $t$?

Пример 1. Функция, заданная параметрически:

Перебирая разные $t\in \mathbb$, мы будем получать точки с координатами $\left( x;y \right)$, которые в итоге превратятся в график:

Да это же тригонометрическая окружность! Она задаётся уравнением $<^<2>>+<^<2>>=1$.

График такого уравнения не является функцией (если забыли почему, гляньте урок про графики уравнений с двумя переменными). Но его можно «составить» из графиков двух функций:

А вот это уже привычные нам аналитические функции, и для них можно посчитать производную!

К сожалению, далеко не всегда параметрическое уравнение вида

\[\left\ < \begin& x=\varphi \left( t \right) \\ & y=\psi \left( t \right) \\ \end \right.\]

можно свести к привычными выражениям вида $y=f\left( x \right)$. Но это ни в коем случае не означает, что для таких параметрических функций нельзя посчитать производную. Можно и даже нужно. И поможет нам в этом следующая формула.

2. Производная функции, заданной параметрически

Итак, основная теорема.

Теорема 1. Пусть функция $y=f\left( x \right)$ задана параметрически:

\[\left\ < \begin& x=\varphi \left( t \right) \\ & y=\psi \left( t \right) \\ \end \right.\]

Тогда производная этой функции считается по формуле

Эту теорему очень легко доказать. В самом деле, если функция $x=\varphi \left( t \right)$ рассматривается на интервале $t\in \left( a;b \right)$ таком, что существует обратная функция $t=<<\varphi >^<-1>>\left( x \right)$, то можно определить сложную функцию

\[y\left( x \right)=\psi \left( <<\varphi >^<-1>>\left( x \right) \right)\]

По теореме о производной сложной функции:

Но по теореме об обратной функции $<<‘>_>=<1>/<<<<‘>>_>>\;$, поэтому

Что и требовалось доказать.

Замечание. Когда выражение дифференцируется по разным переменным, целесообразно указывать в нижним индексе ту переменную, по которой выполняется дифференцирование: $<<‘>_>$, $<<‘>_>$, $<<‘>_>$ и т.д.

Это поможет избежать недоразумений и глупых вычислительных ошибок. Кроме того, подобные обозначения активно используются в дифференциальном исчислении функций нескольких переменных.

Детальное руководство по работе с нижними индексами и переменными дифференцирования — см. урок «Производная сложной функции». Сейчас просто отметим, что мы привыкли считать производную по переменной $x$. Но с тем же успехом можно считать производную и по $t$, и по какому-нибудь $\varphi $, и вообще по любой переменной, которую мы увидим в функции.

2.1. Примеры

Приведённые выше формулы могут показаться сложными и страшными. Но на деле это одна из самых лёгких тем в производных. Взгляните:

Теперь считаем $<<‘>_>$ по формуле производной параметрической функции:

Вот и всё! Готовое выражение можно разбить на две дроби, а можно оставить и так.

Вместо многочленов видим показательные функции. Это ничего не меняет, снова считаем $<<‘>_>$ и $<<‘>_>$:

Теперь находим $<<‘>_>$ по формуле:

Для решения этого задания пришлось вспомнить производную показательной функции и некоторые свойства степеней.:)

Здесь переменной-параметром является $\varphi $, а буквы $a$ и $b$ — просто числа, которые будут частью ответа. Считаем $<<‘>_<\varphi >>$ и $<<‘>_<\varphi >>$ — производные тригонометрических функций:

2.2. Производная в точке

Понятно, что это были совсем простые задачи. Буквально через минуту мы рассмотрим примеры посерьёзнее, но сначала важное дополнение.

Часто нам требуется посчитать не производную функции вообще, а лишь в конкретной точке. Например, чтобы провести касательную или нормаль к кривой, заданной параметрически, в некой точке $<_<0>>\left( <_<0>>;<_<0>> \right)$, лежащей на этой кривой.

В этом случае задача ещё более упрощается.

\[\begin & x\left( t \right)=t\cdot \left( t\cos t-2\sin t \right) \\ & y\left( t \right)=t\cdot \left( t\sin t+2\cos t \right) \\ \end\]

Задача явно серьёзнее, чем все предыдущие. Считаем $<<‘>_>$ и $<<‘>_>$:

И сразу подставляем $t=<\pi >/<4>\;$:

Разумеется, можно было сначала найти общую формулу для $<<‘>_>$, а уже затем подставить в неё $t=<\pi >/<4>\;$ — результат получится точно такой же.

3. Типичные ошибки при вычислении производных

А теперь, пожалуй, ключевой момент, связанный с дифференцированием параметрических функций. Ошибка, которую я сам допустил много лет назад.

Давайте ещё раз взглянем на функцию, заданную параметрически:

\[\left\ < \begin& x=\varphi \left( t \right) \\ & y=\psi \left( t \right) \\ \end \right.\]

И на производную этой функции:

А теперь представьте, что надо посчитать вторую производную: $<<»>_>$. И тут у многих проскакивает мысль: а что если взять формулу для первой производной и просто увеличить в ней количество «штрихов»?

Получится что-то типа вот этого:

Так вот: эта формула не верна!

Чтобы правильно найти вторую производную функции, заданной параметрически, достаточно вспомнить, что вторая производная — это просто производная от производной:

Проще говоря, сначала мы находим $<<‘>_>$ — это будет какая-то функция от $t$. Затем уже от этой функции вновь считаем производную — всё по той же формуле, которую мы сегодня уже много раз использовали. Получится так:

Тут нас ждёт две новости:

• Хорошая: мы уже знаем $<<‘>_>$. Это значит, что каждая последующая производная будет считаться чуть проще и быстрее;
• Плохая: можно легко запутаться во всех этих штрихах и переменных.

Чтобы разобраться с плохой новостью, достаточно просто небольшой практики. Поэтому сейчас мы разберём три примера. А точнее, три задачи из контрольных работ МГТУ им. Баумана. А там знают толк в производных.:)

1. Сначала находим первую производную. Для этого считаем $<<‘>_>$ и $<<‘>_>$:

Откуда находим саму производную $<<‘>_>$:

2. Теперь находим вторую производную. Для этого считаем $<<\left( <<<‘>>_> \right)>^<\prime >>_$:

Кроме того, мы уже знаем $<<‘>_>$. Поэтому находим вторую производную $<<»>_>$:

Вторая производная найдена.

Для сравнения посчитаем «производную» по неправильной формуле:

Получили совершенно другое выражение, которое не является второй производной.

Итак, вторая производная считается из первой ровно по той же формуле, по какой первая производная считается из исходной функции.

Замечание. Когда освоитесь с основной формулой, выкладки можно сократить буквально до двух строк:

Впрочем, не стоит увлекаться сокращением выкладок, если у вас есть хоть малейшее сомнение или недопонимание на любом этапе вычислений.

Пара дополнительных минут — сомнительная экономия по сравнению с парой баллов на контрольной. И уж тем более по сравнению с недопониманием материала.

Дифференцирование арктангенса дробно-рациональной функции — довольно громоздкие действия. Тут в пару строк не уложиться.

Первая производная $<<‘>_>$:

Замечание. При делении дробных выражений полезно заменять их умножением на обратное:

Именно так мы и поступили при вычислении $<<‘>_>$ и $<<»>_>$ в последнем примере. И не только в последнем.:)

4. Третья производная

Пример 8. Найдите производную третьего порядка $<<»’>_>$ для функции, заданной параметрически:

Решение будет состоять из трёх шагов.

1. Найдём первую производную $<<‘>_>$. Для этого считаем $<<‘>_>$ и $<<‘>_>$:

Первая производная $<<‘>_>$ равна

2. Считаем вторую производную. При этом $<<‘>_>$ уже посчитано, осталось найти $<<\left( <<<‘>>_> \right)>^<\prime >>_$:

Находим вторую производную по всё той же формуле:

3. Считаем третью производную. Вновь нужно лишь найти $<<\left( <<<»>>_> \right)>^<\prime >>_$:

Для сокращения вычислений я сразу записал готовую формулу $<<\left( <<<»>>_> \right)>^<\prime >>_$ — проверьте её самостоятельно. А дальше вновь используем формулу производной для параметрической функции:

Задача решена. Хотя вычислений получилось довольно много.

В любом случае помните главную формулу:

И помните, что вторая производная не равна частному вторых производных:

Попытка использовать эту формулу для нахождения производных высших порядков будет считаться грубой ошибкой.