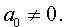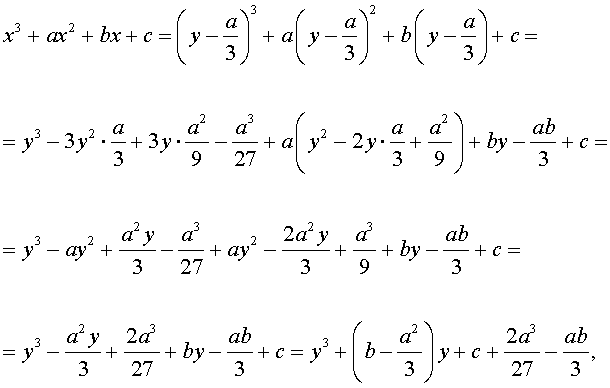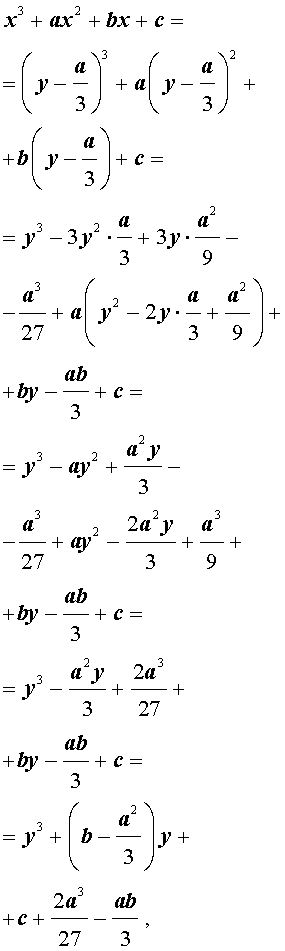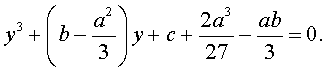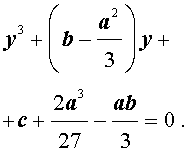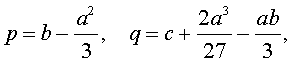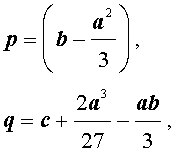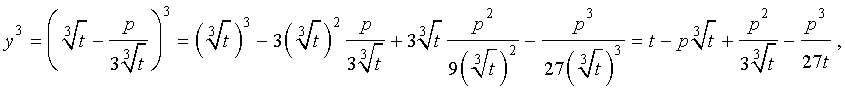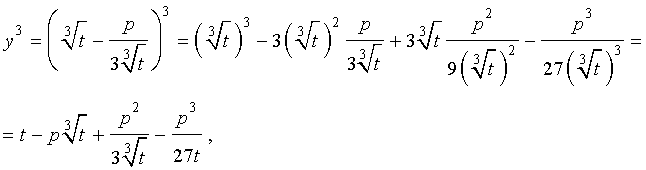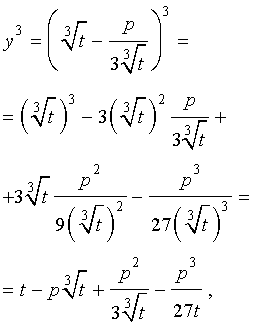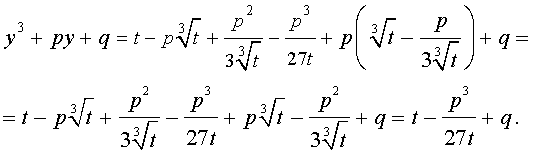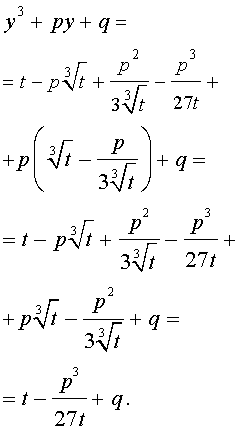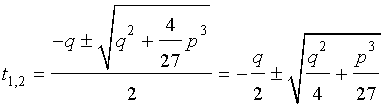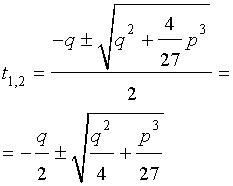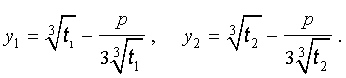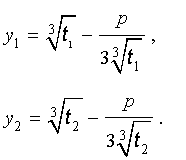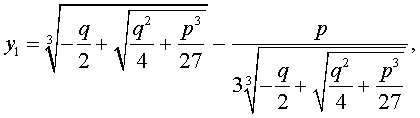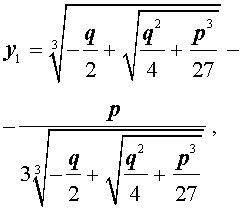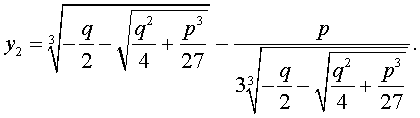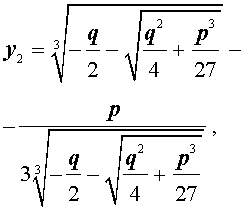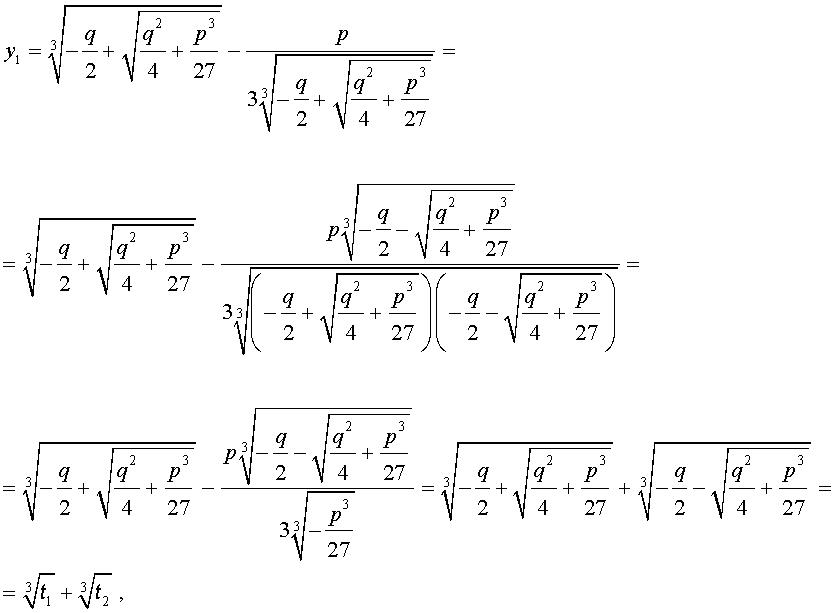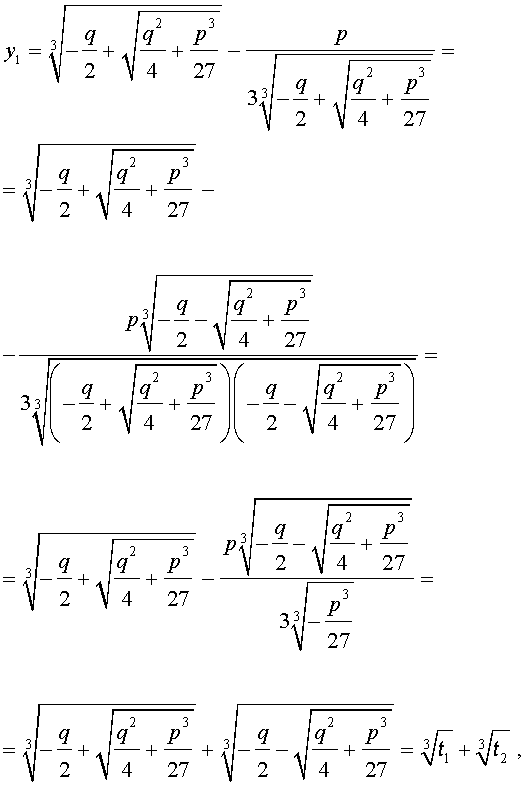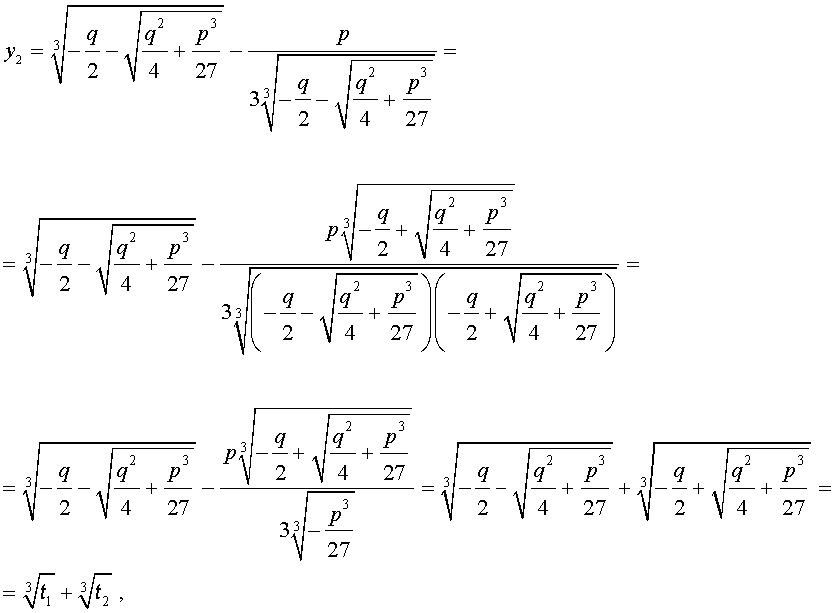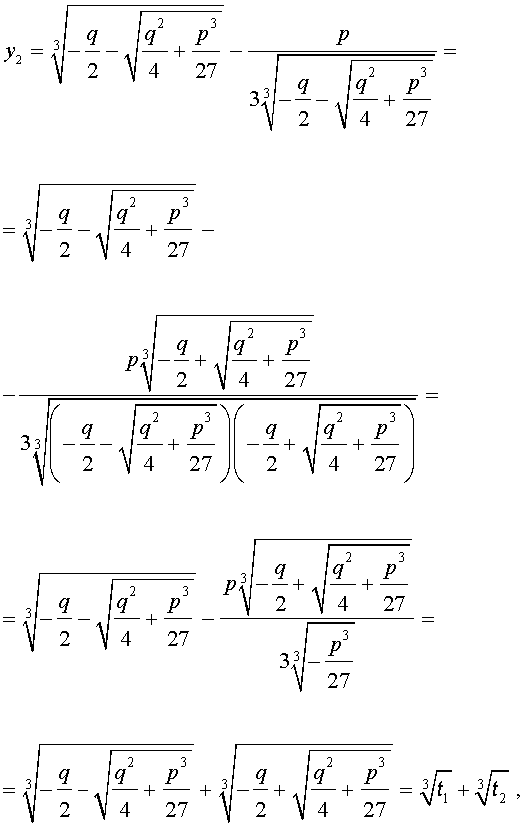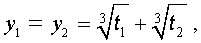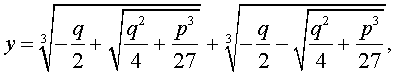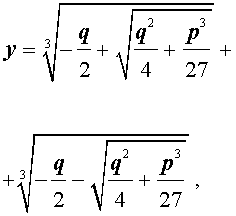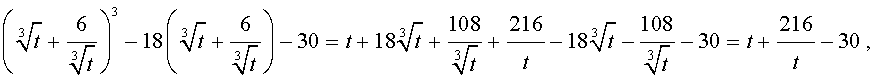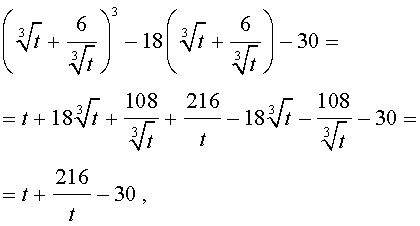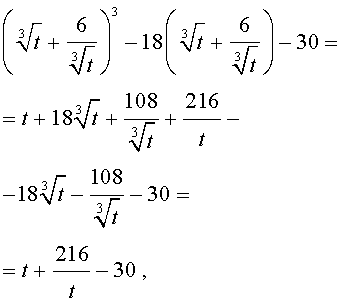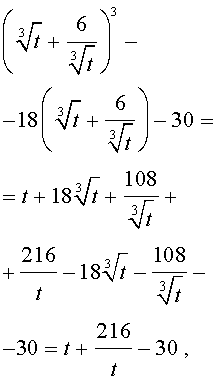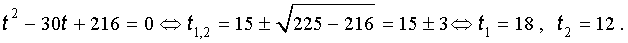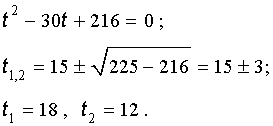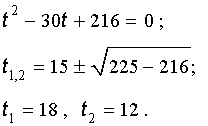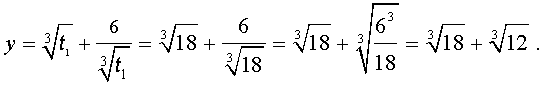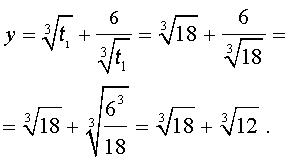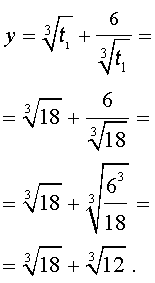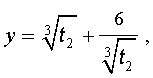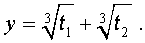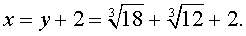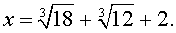Урок алгебры в 10-м классе (занятие элективного курса) по теме «Методы решения уравнений высших степеней»
Презентация к уроку
На занятии изучается методика решения уравнений высших степеней. Рассматриваются два метода: разложение на множители и замена переменной. Понижение степени уравнений с помощью деления многочленов по схеме Горнера и приведение различных уравнений к замене переменной. Дана историческая справка исследования уравнений высших степеней. Представлена презентация урока.
Метод разложения на множители.
Этот метод основан на применении теоремы Безу. Если число α является корнем многочлена P(x) степени n, то его можно представить в виде P(x) = (x — α)Q(x), где Q(x) — многочлен степени (n-1).Теорема Безу: “Остаток от деления многочлена Р(х) на двучлен (x — α) равен P(α), т.е. значению многочлена при x = α” Таким образом, если известен хотя бы один корень уравнения Р(х)=0 степени n, то с помощью теоремы Безу можно свести задачу к решению уравнения степени (n-1), понизить степень уравнения. Теорема. Пусть несократимая дробь p/q является корнем уравнения a0x n + a1x n-1 + . + ax-1x+ an = 0 с целыми коэффициентами, тогда число p – является делителем свободного члена an, а q – делителем старшего коэффициента a0. У многочлена с целыми коэффициентами целые корни являются делителями свободного члена. Таким образом, зная корень многочлена, его легко разложить на множители, т.е. разделить P(x) на (x — α) “углом” или по схеме Горнера.
Решение уравнения с помощью понижения степени. Деление многочлена на многочлен столбиком
Деление многочлена на многочлен столбиком
Для решения уравнение вида Р(х)=0, где Р(х) — многочлен степени n>2, часто применяют метод понижения степени. Он основывается на таком факте: если число x=b является корнем многочлена P(x), то есть P(b)=0, то многочлен P(x) делится без остатка на двучлен x-b.
После того, как мы разделим многочлен P(x) степени n на двучлен x-b, то мы получим многочлен степени n-1, то есть на единицу меньшей исходного. И дальше процедуру можно повторить.
Если старший коэффициент многочлена P(x) равен 1, то корни многочлена P(x) мы ищем среди делителей свободного члена.
Решим уравнение 
Свободный член многочлена в левой части уравнения равен 10.
Делители числа 10: 1; 2; 5; 10.
Проверим, является ли какое-либо из этих чисел корнем многочлена. Для этого последовательно подставим эти значения вместо х в многочлен.
является корнями многочлена 
, и он делится на двучлены 
и 
без остатка.
Разделим многочлен на двучлен x-2 столбиком:
Решение кубических уравнений. Формула Кардано
 Схема метода Кардано |
| Приведение кубических уравнений к трехчленному виду |
| Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи |
| Формула Кардано |
| Пример решения кубического уравнения |
Схема метода Кардано
Целью данного раздела является вывод формулы Кардано для решения уравнений третьей степени ( кубических уравнений )
| a0x 3 + a1x 2 + + a2x + a3= 0, | (1) |
где a0, a1, a2, a3 – произвольные вещественные числа, 
Вывод формулы Кардано состоит из двух этапов.
На первом этапе кубические уравнения вида (1) приводятся к кубическим уравнениям, у которых отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями .
На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям.
Приведение кубических уравнений к трехчленному виду
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x 3 + ax 2 + bx + c = 0, | (2) |
где a, b, c – произвольные вещественные числа.
Заменим в уравнении (2) переменную x на новую переменную y по формуле:
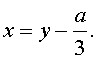 | (3) |
то уравнение (2) примет вид
В результате уравнение (2) примет вид
Если ввести обозначения
то уравнение (4) примет вид
| y 3 + py + q= 0, | (5) |
где p, q – вещественные числа.
Уравнения вида (5) и являются трёхчленными кубическими уравнениями , у которых отсутствует член со второй степенью неизвестного.
Первый этап вывода формулы Кардано завершён.
Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи
Следуя методу, примененому Никколо Тартальей (1499-1557) для решения трехчленных кубических уравнений, будем искать решение уравнения (5) в виде
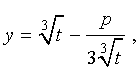 | (6) |
где t – новая переменная.
то выполнено равенство:
Следовательно, уравнение (5) переписывается в виде
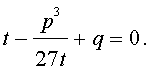 | (7) |
Если теперь уравнение (7) умножить на t , то мы получим квадратное уравнение относительно t :
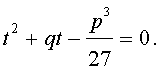 | (8) |
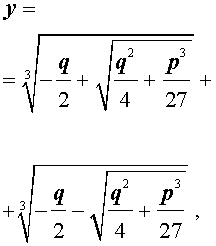
Формула Кардано
Решение уравнения (8) имеет вид:
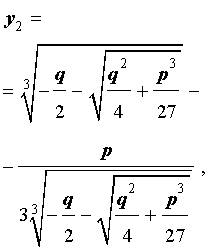
В соответствии с (6), отсюда вытекает, что уравнение (5) имеет два решения:
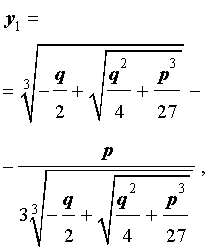
В развернутой форме эти решения записываются так:
Покажем, что, несмотря на кажущиеся различия, решения (10) и (11) совпадают.
С другой стороны,
и для решения уравнения (5) мы получили формулу
которая и называется «Формула Кардано» .
Замечание . Поскольку у каждого комплексного числа, отличного от нуля, существуют три различных кубических корня, то, для того, чтобы избежать ошибок при решении кубических уравнений в области комплексных чисел, рекомендуется использовать формулу Кардано в виде (10) или (11).
Пример решения кубического уравнения
Пример . Решить уравнение
| x 3 – 6x 2 – 6x – 2 = 0. | (13) |
Решение . Сначала приведем уравнение (13) к трехчленному виду. Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену
| x = y + 2. | (14) |
Следовательно, уравнение (13) принимает вид
| y 3 – 18y – 30 = 0. | (15) |
Теперь в соответствии с формулой (6) сделаем в уравнении (15) еще одну замену
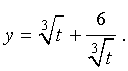 | (16) |
то уравнение (15) примет вид
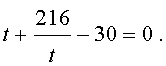 | (17) |
Далее из (17) получаем:
Отсюда по формуле (16) получаем:
Заметим, что такое же, как и в формуле (18), значение получилось бы, если бы мы использовали формулу
или использовали формулу
Далее из равенства (18) в соответствии с (14) получаем:
Таким образом, мы нашли у уравнения (13) вещественный корень
Замечание 1 . У уравнения (13) других вещественных корней нет.
Замечание 2 . Поскольку произвольное кубическое уравнение в комплексной области имеет 3 корня с учетом кратностей, то до полного решения уравнения (13) остается найти еще 2 корня. Эти корни можно найти разными способами, в частности, применив вариант формулы Кардано для области комплексных чисел. Однако применение такого варианта формулы Кардано значительно выходит за рамки курса математики даже специализированных математических школ.
http://ege-ok.ru/2012/08/29/delenie-mnogochlena-na-mnogochlen-stolbikom
http://www.resolventa.ru/spr/algebra/cardano.htm