Формула уравнения движения тела по оси x

Уравнение движения материальной точки

Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.

Имеет смысл говорить только о движении в некоторой системе отсчета.

Система отсчета. Системы координат

Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.

В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x , y , z – ее координат. Могут быть применены другие:

• сферическая система с положением точек и ее радиус-вектором, определенных координатами r , υ , φ ;
• цилиндрическая система с координатами p , z , α ;
• на полярной плоскости с параметрами r , φ .

В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.

Кинематическое уравнение движения материальной точки

Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.

При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.

Это возможно при использовании кинематического уравнения движения:

Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.

Ее перемещение по уравнению ( 1 ) определено, если имеется указанное положение в любой момент времени t . Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:

x ( t ) = x , y ( t ) = y , z ( t ) = z ( 2 ) .

Прямоугольные декартовы координаты x , y , z — это проекции радиус-вектора r ¯ , проведенного из начала координат. Очевидно, что длину и направление r ¯ можно найти из соотношений, где a , β , γ являются образованными радиус-вектором углами с координатными осями.

Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах.

Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости О х у , тогда применимы полярные координаты r , φ , относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:

r = r ( t ) , φ = φ ( t ) ( 3 ) .

Кинематическое уравнение движения точки в криволинейных координатах q 1 , q 2 , q 3 , связанных с декартовыми преобразованиями вида x = x ( q 1 , q 2 , q 3 ) , y = y ( q 1 , q 2 , q 3 ) , z = z ( q 1 , q 2 , q 3 ) ( 4 ) , записывается как

q 1 = q 1 ( t ) , q 2 = q 2 ( t ) , q 3 = q 3 ( t ) ( 5 ) .

Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями ( 2 ) , ( 5 ) . Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.

Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:

Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.

Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.

Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.

Дано уравнение движения материальной точки x = 0 , 4 t 2 . Произвести запись формулы зависимости υ x ( t ) , построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление.

Дано: x = 0 , 4 t 2 , t = 4 c

Найти: υ x ( t ) , S — ?

Решение

При решении необходимо учитывать зависимость скорости от времени:

υ x = υ 0 x + a x t .

Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:

x = x 0 + υ 0 x t + a x t 2 2 , x = 0 , 4 t 2 .

Очевидно, что x 0 = 0 , υ 0 x = 0 , a x = 0 , 8 м / с 2 .

После подстановки данных в уравнение:

Определим точки, изобразим график:

υ x = 0 , t = 0 , υ x = 4 , t = 5

Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы:

Механическое движение

О чем эта статья:

Механическое движение

Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.

Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.

«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:

• тело отсчета
• система координат
• часы

В совокупности эти три параметра образуют систему отсчета.

В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉

Прямолинейное равномерное движение

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.

Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.

Мы можем охарактеризовать это движение следующими величинами.

Скалярные величины (определяются только значением)

• Время — в международной системе единиц СИ измеряется в секундах [с].
• Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].

Векторные величины (определяются значением и направлением)

• Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
• Перемещение — вектор, проведенный из начальной точки пути в конечную [м].

Проецирование векторов

Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.

Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.

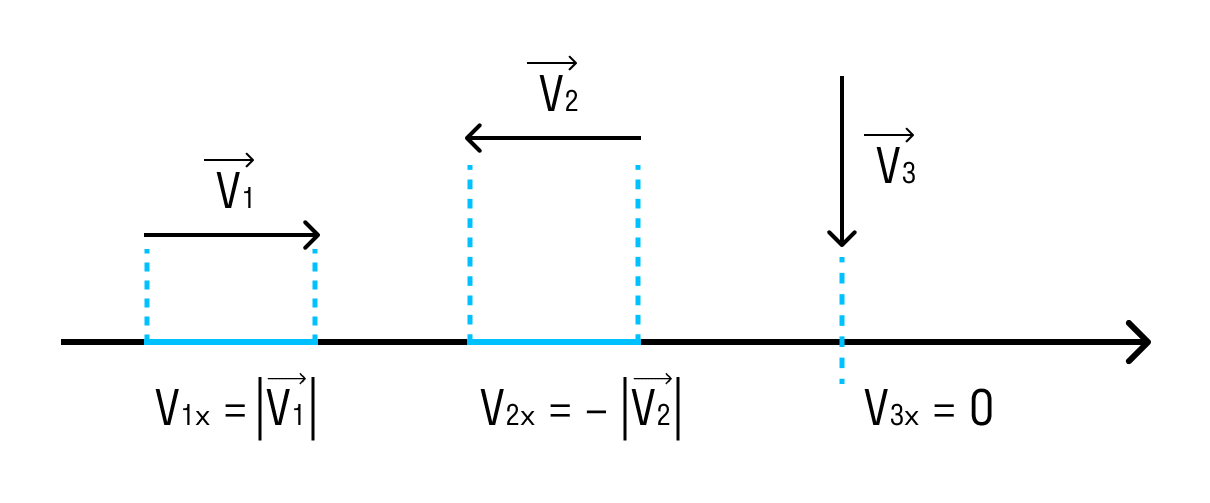
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.

Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.

Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.

Скорость

— скорость [м/с]
— перемещение [м]
— время [с]

Средняя путевая скорость

V ср.путевая = S/t

V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]

Задача

Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.

Решение:

Возьмем формулу средней путевой скорости
V ср.путевая = S/t

Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч

Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч

Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!

Уравнение движения

Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).

Уравнение движения

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_x — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v

Уравнение движения при движении против оси

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_x — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».

Итак, равноускоренное прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.

Уравнение движения для равноускоренного движения

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_0x — начальная скорость тела в [м/с]
t — время [с]
a_x — ускорение [м/с 2 ]

Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:

Формула конечной скорости

— конечная скорость тела [м/с]
— начальная скорость тела [м/с]
— время [с]
— ускорение [м/с 2 ]

Задача

Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

Так как автобус двигался с места, . Значит

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч 2
Теперь возьмем уравнение движения.
x(t) = x₀ + v_0xt + a_xt 2 /2

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:
км

Ответ: через полчаса координата автобуса будет равна 150 км.

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с 2 , а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с 2 . В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с 2 .

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

Равномерное движение

Школьный курс физики содержит раздел «кинематика». Большинство задач этого раздела можно решить, рассматривая движение вдоль одной оси — одномерное движение. Его еще называют прямолинейным движением.

Для некоторых задач нужно рассматривать движение на плоскости – двумерный случай.

Вообще, движение тела может происходить:

• вдоль оси – одномерный случай, ось часто именуют, как «Ox»;
• на плоскости;
• в трехмерном пространстве;

Здесь рассмотрим одномерный случай движения — движение тел вдоль оси.

Параметры, описывающие движение

Чтобы описать движение, используют:

• перемещение тела;
• время, в течение которого движение происходило;
• скорость тела;
• начальные и конечные координаты тела;
• траекторию тела;

Траектория – линия, вдоль которой двигалось тело.

Траектория – скаляр, в СИ длину траектории измеряют в метрах.
Для криволинейного движения траектория будет отрезком кривой.
Если движение прямолинейное, траектория – отрезок прямой линии.

Перемещение тела – это вектор. Он соединяет точки, в которых тело находилось в начале и конце движения, направлен из начальной точки в конечную.
Модуль этого вектора – его длину, в СИ измеряют в метрах.

Может ли перемещение тела равняться нулю, при том, что траектория имеет какую-либо протяженность?
Да, такое может быть. Когда тело движется так, что в конце движения оно вернется в начальную точку, в которой находилось перед началом движения.
Если в завершении движения тело окажется на каком-то расстоянии от начальной точки, длина вектора перемещения будет положительной.

Примечания:

• Модуль (длина) вектора не бывает отрицательным, он либо положительный, либо нулевой.
• Когда тело движется по прямой и не меняет направление, длина траектории совпадает с длиной (модулем) перемещения.

Уравнение движения — описывает характер движения.

• время движения,
• начальную и конечную координаты тела и
• его скорость.

Вместо координат тела уравнение движения может содержать перемещение.

Примечания:

1. Координаты тела, время движения и траектория – это скалярные величины.
2. А скорость тела, его ускорение и перемещение – это векторы.
3. Когда движение равномерное, скорость тела не меняется.
4. Скорость отвечает на вопрос: как быстро изменяется координата (или путь, перемещение).

Описанные параметры применяют и для равномерного и для неравномерного движения.

Прямолинейное движение вдоль оси

Рассмотрим движение по прямой, когда скорость тела не меняется. Это — равномерное прямолинейное движение.

На рисунке 1 представлено движение тела вдоль оси, назовем ее для определенности Ox:

Ось «Ox» на рисунке 1 обозначена большим символом «X».
Точка, в которой тело находилось в начале движения \(x_ <0>\left( \text <м>\right)\) — начальная координата тела;
В эту точку тело переместилось к концу движения \(x \left( \text <м>\right)\) — конечная координата тела;
Расстояние между двумя точками \(S \left( \text <м>\right)\) – это перемещение тела. Перемещение – это вектор.

Формула перемещения для одномерного случая

Для движения по оси (одномерный случай), длину перемещения находят так:
\[ \large \boxed < S = \left| x — x_<0>\right| >\]
Знак модуля нужен для того, чтобы длина перемещения оставалась положительной, даже, если движение происходит влево по оси, т. е. против направления оси Ox.
Сравним два случая движения тел. Первый – в положительном направлении оси Ox (рис 2а), второй – в направлении, противоположном оси (рис 2б).

Чтобы найти длину вектора перемещения при движении в положительном направлении оси (рис. 2а), модуль раскрываем так:
\[ S = \left| x — x_ <0>\right| = x — x_ <0>\]
Для движения в отрицательном направлении оси (рис. 2б), длина вектора перемещения выражается так:
\[ S = \left| x — x_ <0>\right| = — \left( x — x_ <0>\right) = x_ <0>— x \]
И в первом, и во втором случае, длина (модуль) вектора перемещения окажется положительной.

Скорость равномерного движения

В учебниках физики равномерному движению дают такое определение:
Движение равномерное, когда тело за одинаковые интервалы времени проходит равные расстояния.

Упростим формулировку:
Если каждую секунду тело проходит одинаковые расстояния – оно движется равномерно.

Слово «равномерное» состоит из двух частей.
Если разбить его на части, получим
«равно» — одинаковый, равный,
«мерное» — отмерять.
Или, другими словами: каждую секунду отмеряем одинаковые расстояния (рис. 2).

Для равномерного движения тела его

• перемещение,
• время движения и
• скорость,

\[ \left|\vec \right| = \left|\vec \right|\cdot t \]

Эта формула называется уравнением движения. Или, развернуто: «уравнение равномерного прямолинейного движения».

Где \( \left|\vec \right| \) — длина (модуль) вектора перемещения и, \(\left|\vec \right|\) — длина (модуль) вектора скорости.

Уравнение движения можно записать проще:

\(S \left( \text <м>\right)\) – расстояние, пройденное телом (перемещение).

\(t \left( c \right)\) – промежуток времени, в течение которого тело двигалось.

\(v \left( \frac<\text<м>> \right)\) – скорость, с которой двигалось тело.

Разделив обе части уравнения \( S = v \cdot t \) на интервал времени \( t \), получим выражение для скорости тела:

График уравнения равномерного движения

Вспомним, что перемещение является разностью конечных и начальных координат тела

\( S = \left| x — x_ <0>\right| \)

Воспользуемся тем, что при движении вдоль положительного направления оси модуль можно раскрыть так:

\( \left| x — x_ <0>\right| = x — x_ <0>\)

Тогда уравнение движения перепишем так:

\[ \large \boxed < x — x_<0>= v \cdot t >\]

Прибавим к обеим частям уравнения величину \( x_ <0>\). Получим такую запись

\[ \large x = v \cdot t + x_<0>\]

Это уравнение задает на плоскости tOx линию. Ее график на осях «x» и «t» — это прямая линия.

Вспомним, что для прямой линии в математике применяют такой вид записи:

Сравним два уравнения:

\[ \begin x = v\cdot t + x_<0>\\ y = k\cdot x + b \end \]

Видно, что число \( x_<0>\) – начальная координата тела, выполняет роль коэффициента \(b\).

А скорость тела \( v\) – играет роль углового коэффициента \(k\).

Сравним графики линий (рис. 4), описанных соотношениями \( y = k \cdot x + b\) и \( x = v \cdot t + x_<0>\)

Видно, что линия на рисунке 4а, располагается и слева и справа от вертикальной оси.

Линия же, описывающая движение тела, представленная на рисунке 4б, располагается только лишь в правой полуплоскости. Это не с проста. На горизонтальной оси рисунка 4б отложено время, а в левой полуплоскости время будет отрицательным. При решении задач физики мы считаем, что в начальный момент задачи время равно нулю. Поэтому, область отрицательного времени в физике нас не интересует.

Рассмотрим теперь на графике равномерное движение двух тел, обладающих разными скоростями (рис. 5). Движение тела 1 на рисунке описывает синяя линия, а тела 2 – красная.

Два тела стартуют из точки \( x_<0>\) и двигаются равномерно воль оси Ox. За промежуток времени \( \Delta t\) тело 1, проходит больший путь, чем тело 2.

Примечание: Чем сильнее на графике x(t) прямая линия прижимается к вертикали, тем больше скорость, с которой движется тело!

Как отмечалось выше, тело может двигаться не только в положительном направлении вдоль оси, но и в отрицательном направлении.

На следующем рисунке представлены случаи движения тела в положительном (рис. 6а) и, в отрицательном (рис. 6б) направлениях оси Ox.

Когда скорость направлена по оси (рис. 6а) — координата «x» увеличивается,

а когда против оси (рис. 6б) — координата «x» уменьшается.

На рисунке рядом с прямыми x(t) приведены уравнения движения. Когда скорость направлена против оси (рис. 6б), перед ней записывают знак «минус».

Угол \(\alpha\) на рисунке связан со знаком скорости. Если скорость направлена по оси (рис. 6а), то угол будет острым. А если скорость направлена против оси (рис. 6б) – угол тупой.

Примечание: Скорость – это вектор. Когда вектор направлен против оси, его проекция на эту ось будет отрицательной. Читайте тут о проекциях векторов. Длина любого вектора – это положительная величина.

Как по графику перемещения определить скорость

Пользуясь графиком функций S(t), или x(t) равномерного движения можно определить скорость, с которой движется тело.

Примечания:

• График S(t) называют так: «зависимость перемещения S от времени t», или кратко — график перемещения от времени.
• А график x(t) — так: «зависимость координаты x от времени t», или кратко — график координат от времени.

Скорость находим за четыре шага (рис. 7):

1. Выбираем две точки на линии, описывающей движение и определяем их координаты;
2. Находим разность вертикальных координат;
3. После находим разность координат по горизонтали;
4. Делим «вертикаль» на «горизонталь»

Полученное число и будет скоростью тела.

Примечания:

• Когда просят найти скорость, обычно имеют ввиду, что нужно найти модуль вектора скорости.
• Скорость в системе СИ измеряют в метрах, деленных на секунду.

Обращаем внимание на то, в каких единицах на осях измерены расстояние S и время t. Если нужно, переводим расстояние в метры, а время — в секунды, чтобы получить скорость в правильных единицах измерения.

Рассмотрим рисунок 7.

На рисунке первая точка имеет координаты \( \left( t_ <1>; x_ <1>\right) \),

координаты второй точки: \( \left( t_ <2>; x_ <2>\right) \).

Разницы между координатами находим, руководствуясь принципом («конечная» — «начальная») по формулам

\( \Delta t = t_ <2>— t_ <1>\)

\( \Delta x = x_ <2>— x_ <1>\)

Скорость вычислим из соотношения

Читайте далее о том, как переводить скорость из километров в час в метры в секунду и о равнопеременном движении