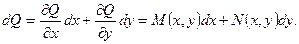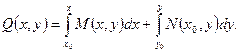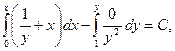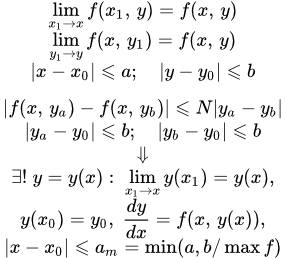Формулировка задачи коши для уравнения первого порядка

Дифференциальные уравнения первого порядка. Постановка задачи Коши.

Рассмотрим дифференциальное уравнение первого порядка.

Общий вид уравнения первого порядка

Если это уравнение разрешить относительно 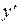, то есть

(12)

то уравнение называется уравнением первого порядка, разрешенным относительно производной.

Определение 4.Общим решением дифференциального уравнения (12) называется дифференцируемая функция

(13)

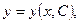
которая зависит от одной произвольной постоянной С и обращает это уравнение в тождество.

Определение 5. Частным решением уравнения (12) называется решение, получаемое из общего решения (13) при каком-либо определенном значении произвольной постоянной С.

Рассмотрим дифференциальное уравнение первого порядка в симметричной относительно x и y форме:

(14)

При некоторых условиях уравнение (3) эквивалентно, по крайней мере, одному из дифференциальных уравнений вида:

Дифференциальное уравнение определяет в каждой точке (x,y), где существует функция f(x,y), значение то есть угловой коэффициент касательной к интегральной кривой в этой точке. Таким образом, дифференциальное уравнение (12) определяет поле направлений.

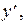
Задачи интегрирования дифференциального уравнения заключаются в том, чтобы найти интегральные кривые, направления касательных к которым в каждой точке совпадают с направлением поля. Для построения интегральных кривых используют метод изоклин.

Определение 6. Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым сохраняют постоянное направление.

Семейство изоклин дифференциального уравнения (12) определяется уравнением

, (15)

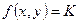
Постановка задачи Коши.

Задача о нахождении частного решения дифференциального уравнения, удовлетворяющего некоторым дополнительным условиям, часто встречается в приложениях. Если эти условия относятся к одному и тому же значению аргумента искомой функции, то их называют начальными. В том случае, когда начальные условия для дифференциального уравнения состоят в задании фиксированных значений функции и ее производных, их называют условиями Коши, а задачу – задачей Коши.

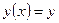
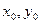
Задачей Коши для дифференциального уравнения (12) называют задачу нахождения решения уравнения удовлетворяющего начальному условию (где — заданные числа, называемые начальными значениями или данными).

Геометрически это означает, что ищется интегральная кривая, проходящая через заданную точку плоскости XOY.

Теорема. (о существовании и единственности решений задачи Коши.)

Пусть функция и ее производные определены и непрерывны на открытом множестве . Тогда в некоторой окрестности точки существует непрерывное решение задачи Коши:

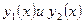
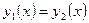
Замечание. Это решение единственно, т.е. если — два непрерывных решения задачи Коши, то для всех значений, при которых эти решения определены.

Как известно, общее решение уравнения (12) задается следующим равенством

(16)

Чтобы выделить частное решение уравнения (12), достаточно знать значение первообразной в какой – либо точке. Пусть, например, Тогда из соотношения (16) имеем или , т. е. решение единственно и равно

(17)

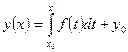
Уравнение (17) называется частным решением задачи Коши.

Пример 3. Решить задачу Коши.

Решение. Согласно формуле (17) частное решение имеет вид

Классы дифференциальных уравнений, интегрируемых в квадратурах.

Определение 7. Дифференциальное уравнение первого порядка называется интегрируемым в квадратурах (или просто интегрируемым), если его общее решение может быть получено с помощью конечного числа алгебраических операций и квадратур.

Рассмотрим уравнение (14).

Определение 8. Уравнение (14) называется точным уравнением или уравнением в полных дифференциалах, если существует дифференцируемая функция , для которой левая часть уравнения (14) является полным дифференциалом, т.е.

Пример 4. Для уравнения общий интеграл записывается в виде (это легко проверить непосредственным дифференцированием). Очевидно, что интегральные линии, определяемые общим интегралом, являются концентрическими окружностями с центром в начале координат.

Теорема. Пусть функции 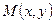и непрерывно дифференцируемы на открытом множестве D. Для того чтобы уравнение (14) было точным необходимо, чтобы выполнялось условие

(18)

Доказательство. Пусть уравнение (14) является точным. Тогда из определения точного уравнения и понятия полного дифференциала вытекает, что

(19)

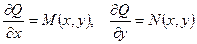
Дифференцируя первое равенство по y, а второе – по x, имеем

.

Так как смешанные производные непрерывны, то они равны и, значит, справедливо условие (18). Что и требовалось доказать.

Пусть D – односвязная область. Покажем, что в этом случае условие (18) является достаточным. Проинтегрируем первое из равенств (19) по x, считая y постоянным:

, (20)

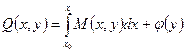
где — постоянная интегрирования, зависящая от y, а — абсцисса любой точки из области единственности D. Подберем функцию так, чтобы выполнялось второе из равенств (19). Для этого продифференцируем равенство (20) по y, считая x постоянным:

Откуда получим

Следовательно, т.е.

(21)

где — ордината произвольной точки из области единственности D, а произвольную постоянную считаем равной нулю. Из соотношений (20) и (21) получим

Итак, если в области D, не содержащей особых точек уравнения (12), выполнено условие (18), то общий интеграл уравнения выражается формулой

(22)

где C – произвольная постоянная.

Пример 5. Решить уравнение .

Решение. Обозначим и проверим выполнение условия (18): т.е. Это уравнение в полных дифференциалах и его общий интеграл имеет вид (22), где — любая точка из области . Положим, например, , тогда

.

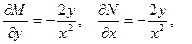
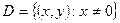
Интегрируя, находим Обозначив через получим общий интеграл исходного уравнения.

Интегрирующий множитель.

В том случае, когда условие (18) не выполняется, уравнение (14) не является уравнением в полных дифференциалах. Однако его можно проинтегрировать, если найти такую функцию , при умножении на которую всех членов уравнения оно становится точным:

(23)

Такая функция называется интегрирующим множителем уравнения (14). Общее решение уравнения (23) совпадает с общим решением уравнения (14).

Докажем, что для всякого уравнения (14), где M и N – непрерывно дифференцируемые функции, существует интегрирующий множитель. Пусть уравнение (14) не является точным. В силу теоремы существования и единственности решения, оно имеет общее решение в неявном виде. Дифференцируя это равенство по x, получим Так как из уравнения (14) следует , то . Обозначим через общую величину этих двух равных отношений; тогда

(24)

Поскольку 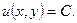есть общий интеграл уравнения (14), имеем Отсюда с учетом соотношения (24) получим уравнение вида (23), которое является точным. Следовательно, — интегрирующий множитель уравнения.

Пример 6. Решить уравнение .

Решение. Проверим выполнение условия (18):

, следовательно, это не уравнение в полных дифференциалах. Составим отношение

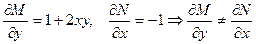
Найдем интегрирующий множитель

Тогда соответствующее точное уравнение будет иметь вид:

Область единственности этого уравнения есть 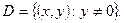Пусть . Находим общий интеграл

откуда, интегрируя, получим

Формулировка задачи коши для уравнения первого порядка

Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах…
Часть II. Глава IV. Обыкновенные дифференциальные уравнения

§ 1. Дифференциальные уравнения первого порядка

1. Основные понятия. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функцию и производные (или дифференциалы) этой функции. Если независимая переменная одна, то уравнение называется обыкновенным; если же независимых переменных две или больше, то уравнение называется дифференциальным уравнением в частных производных.

Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Например:

1) х²у’ + 5xy = у² – обыкновенное дифференциальное уравнение первого порядка;

2) – обыкновенное дифференциальное уравнение второго порядка;

3) y’³ + y»y»’ = х – обыкновенное дифференциальное уравнение третьего порядка;

4) F (х, у, у’, у») = 0 – общий вид обыкновенного дифференциального уравнения второго порядка;

5) – уравнение в частных производных первого порядка.

В этом параграфе рассматриваются обыкновенные дифференциальные уравнения первого порядка, т. е. уравнения вида F (х, у, у’) = 0 или (в разрешенном относительно у’ виде) y’ = f(х, у).

Решением дифференциального уравнения называется такая дифференцируемая функция у = φ (x), которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения.

Общим решением дифференциального уравнения первого порядка у’ = f(x, у) в области D называется функция у = φ(x, C), обладающая следующими свойствами: 1) она является решением данного уравнения при любых значениях произвольной постоянной С, принадлежащих некоторому множеству; 2) для любого начального условия у(х0) = у0 такого, что (x0; y0) ∈ 0, существует единственное значение С = С0, при котором решение у = φ(x, C0) удовлетворяет заданному начальному условию.

Всякое решение у = φ(x, C0), получающееся из общего решения у = φ (x, C) при конкретном значении С = С0, называется частным решением.

Задача, в которой требуется найти частное решение уравнения y’ = f(х, у) удовлетворяющее начальному условию у(х0) = y0, называется задачей Коши.

Построенный на плоскости хОу график всякого решения у = φ(х) дифференциального уравнения называется интегральной кривой этого уравнения. Таким образом, общему решению у = φ(х, С) на плоскости хОу соответствует семейство интегральных кривых, зависящее от одного параметра – произвольной постоянной С, а частному решению, удовлетворяющему начальному условию y(x0) = y0, – кривая этого семейства, проходящая через заданную точку М0(x0; у0).

Если функция f(х, у) непрерывна и имеет непрерывную производную в области D, то решение дифференциального уравнения у’= f (х, у) при начальном условии у(х0) = у0 существует и единственно, т. е. через точку (x0; y0) проходит единственная интегральная кривая данного уравнения (теорема Коши).

Особым решением называется такое решение, во всех точках которого условие единственности не выполняется, т. е. в любой окрестности каждой точки (х; у) особого решения существуют по крайней мере две интегральные кривые, проходящие через эту точку.

Особые решения не получаются из общего решения дифференциального управления ни при каких значениях произвольной постоянной С (в том числе и при С = ± ∞).

Особым решением является огибающая семейства интегральных кривых (если она существует), т. е. линия, которая в каждой своей точке касается по меньшей мере одной интегральной кривой.

Например, общее решение уравнения записывается в виде у = sin (х + С). Это семейство интегральных кривых имеет две огибающие: у = 1 и у = -1, которые и будут особыми решениями.

2. Дифференциальные уравнения с разделяющимися переменными. Дифференциальное уравнение вида

относится к типу уравнений с разделяющимися переменными. Если ни одна из функций f1(x), f2(y), φ1(x), φ2(y) не равна тождественно нулю, то в результате деления исходного уравнения на f2 (x) φ1 (y) оно приводится к виду

Почленное интегрирование последнего уравнения приводит к соотношению

которое и определяет (в неявной форме) решение исходного уравнения. (Решение дифференциального уравнения, выраженное в неявной форме, называют интегралом этого уравнения.)

507. Решить уравнение х(у²-4)dx + y dy = 0.

△ Разделив обе части уравнения на у² – 4 ≠ 0, имеем

x² + ln|у² – 4| = ln|C|, или у² – 4 = Сe -λ²

Это общее решение данного дифференциального уравнения.

Пусть теперь у² – 4 = 0, т. е. у = ± 2. Непосредственной подстановкой убеждаемся, что у = ±2 – решение исходного уравнения. Но оно не будет особым решением, так как его можно получить из общего решения при С = 0. ▲

508. Найти частный интеграл уравнения у’ cos х = у / ln у, удовлетворяющий начальному условию y(0) = l.

△ Полагая , перепишем данное уравнение в виде

Проинтегрируем обе части уравнения:

, или

Используя начальное условие у = 1 при х = 0, находим С = 0. Окончательно получаем

▲

509. Найти общий интеграл уравнения у’ = tg x tg y.

△ Полагая и разделяя переменные, приходим к уравнению ctg у dy = tg х dx. Интегрируя, имеем

, или ln|sin у| = -ln|cos x| + ln С.

Отсюда находим sin y = C/cos x, или sin y / cos x = С (общий интеграл). ▲

510. Найти частное решение дифференциального уравнения (l + x²)dy + y dx = 0 при начальном условии у(1) = 1.

△ Преобразуем данное уравнение к виду . Интегрируя, получим

, или ln |y| = – arctg x + С

Это и есть общий интеграл данного уравнения.

Теперь, используя начальное условие, найдем произвольную постоянную С; имеем ln 1 = — arctg 1 + С, т. е. С = π/4. Следовательно,

ln у = – arctg х + π/4,

откуда получаем искомое частное решение y = e π/4 – arctg x . ▲

Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах… Ч. II. Стр. 117-119.

Теорема Коши существования и единственности решения дифференциального уравнения первого порядка

Впервые существование решения дифференциального уравнения было доказано Коши. Приводимое ниже доказательство основано на методе последовательных приближений, который принадлежит Пикару. Этот метод имеет самостоятельное значение, поскольку позволяет получить приближенное решение дифференциального уравнения.

Формулировка теоремы

Пусть дано дифференциальное уравнение первого порядка:
(1)
с начальным условием
(1.1) .
Пусть – непрерывная функция двух переменных в замкнутой области :

и, следовательно, ограничена некоторым положительным значением :
(2) .
И пусть функция удовлетворяет условию Липшица:
(3) ,
.
Тогда существует единственное решение уравнения (1):
,
удовлетворяющее начальному условию , определенное и непрерывное для значений в интервале:
,
где есть наименьшее из двух чисел и .

Условие Липшица

Рассмотрим условие Липшица. Оно имеет вид:
(3) ,
где – положительное число;
, и – любые значения из области :
, , .

Смысл условия Липшица легко понять, если записать его в виде:
(3.1) .
При некотором фиксированном значении переменной , функция является функцией от переменной : . Пусть мы имеем график этой функции. Возьмем две точки, принадлежащие , на этом графике и проведем через них прямую. Тогда угол между прямой и осью ограничен некоторым значением , которое меньше . При таком ограничении график не имеет вертикальных касательных и скачков. А в тех точках, где существует частная производная , она ограничена:
.

Если в области функция имеет непрерывную частную производную , то в этой области выполняется условие Липшица (3).
Для доказательства заметим, что поскольку частная производная непрерывна в замкнутой области, то она ограничена:
.
По теореме Лагранжа о конечных приращениях, имеем:
,
где частные производные вычисляются в некоторой точке , в которой переменная принадлежат интервалу между и :
.
Тогда:
.

Доказательство существования решения

Приведем исходное уравнение (1) с начальным условием (1.1) к интегральному уравнению. Левая и правая части (1) являются функциями от . Заменим на :
.
Интегрируем это уравнение по от до :
;
Подставим начальное условие . В результате получим интегральное уравнение:
(4) .

Покажем, что интегральное уравнение (4) эквивалентно дифференциальному уравнению (1) с начальным условием (1.1). Для этого нужно показать, что из (1) и (1.1) следует (4) и из (4) следует (1) и (1.1). То, что из (1) и (1.1) следует (4) мы уже показали. Осталось показать, что из (4) следует (1) и (1.1). Для этого подставим в (4) . Получим начальное условие (1.1). Продифференцировав обе части уравнения (4) по , получаем уравнение (1).

Далее мы пытаемся найти решение уравнения (4) с помощью последовательных приближений. Для этого определяем ряд функций от переменной по формулам:
(5.1) ;
(5.2) ;
(5.3) ;
.
(5.n) .
Мы предполагаем, что при , стремится к решению уравнения (4):
(6) ,
где – решение уравнения (4). Если мы докажем это, то мы докажем существование решения.

Доказательство существования решения будем проводить в два этапа:
1> вначале докажем, что предел (6) существует;
2) затем докажем, что удовлетворяет уравнению (4):
.

1) Доказательство существования предела y_n при n стремящемся к бесконечности

Сведем последовательные приближения (5.1) – (5.n) к сумме ряда. Для этого пишем:

.
Таким образом нам нужно доказать, что ряд
(7)
сходится при .

Сначала покажем, что при , последовательные приближения принадлежат интервалу .
Действительно, при имеем:
.
Поскольку есть наименьшее из двух чисел и , то и
.

Далее, поскольку принадлежит интервалу , то . Тогда, аналогично предыдущему,
.
Отсюда
.

Далее, по индукции, поскольку принадлежат интервалу , то и
.
Отсюда
.

Итак, мы доказали, что последовательные приближения принадлежат интервалу
.
Теперь мы можем оценить члены ряда (7), применяя условие Липшица.

Для первого члена имеем:
;
(8.1) .
Для второго члена применяем условие Липшица и оценку (8.1):

;
(8.2) .
Для третьего члена применяем, аналогично, условие Липшица и оценку (8.2):

;
(8.3) .

Далее применим метод индукции. Пусть
(8.n) .
Тогда

;
(8.n+1) .
Итак, поскольку (8.n) справедливо для и из (8.n) следует (8.n+1), то (8.n) выполняется для любых .

Запишем ряд (7) в виде:
(7.1) ,
где .
Применим (8.n) и заменим наибольшим допустимым значением :
.
Тогда каждый член ряда (7.1) ограничен по модулю членом ряда
(9) .
Исследуем ряд (9) на сходимость. Применим признак Даламбера:
.
Итак, ряд (9) сходится. Поскольку все члены ряда (7.1), начиная со второго, по абсолютной величине меньше членов сходящегося ряда (9), то, в силу критерия Вейерштрасса, ряд (7.1) сходится равномерно для всех , удовлетворяющих условию . Поскольку интеграл есть непрерывная функция от верхнего предела, то каждый член ряда (7.1) есть непрерывная функция от . Поэтому предел
(10)
существует и является непрерывной функцией от .

2) Доказательство того, что Y является решением (4)

Рассмотрим уравнение (5.n):
(5.n) .
Докажем, что при , это уравнение стремится к уравнению
(11) .

В силу (10) левая часть уравнения (5.n) стремится к .

Теперь покажем, что
.

Перепишем правую часть (5.n):
.
Далее заметим, что поскольку все принадлежат закрытому интервалу , то и принадлежит этому интервалу, . Поэтому мы можем применить условие Липшица.

Оценим абсолютную величину последнего члена:

.
Поскольку, при , стремится к равномерно, то для любого положительного числа можно указать такое натуральное число , что для всех ,
.
Тогда
.
Поскольку произвольно, то

Поэтому
.
То есть при уравнение
(5.n)
принимает вид
(11) .

Доказательство единственности решения

Предположим, что уравнение
(4)
имеет два решения и , различающиеся в некоторой точке , принадлежащей интервалу .
Рассмотрим функцию
.
Будем считать, что . В противном случае поменяем местами и .
Поскольку и непрерывны, то и непрерывная функция. Поэтому она отлична от нуля в некотором интервале, содержащем точку :
при .
Поскольку , то . То есть точка не принадлежит этому интервалу.

Если , то преобразуем (4) следующим образом:
,
где
.
Если переобозначить постоянные
,
то получим задачу (4), для которой
;
при ,
где – некоторое число, не превосходящее .

Если , то поступаем аналогично:
,
Переобозначим постоянные:
.
Получаем задачу (4), для которой
;
при ,
где – некоторое число, не меньшее .

Итак, мы имеем:
;
при ( или при ).
Далее возьмем произвольное положительное число ( или ) и рассмотрим закрытый интервал ( или ). Поскольку функция непрерывна, то она достигает наибольшего значения в одной из точек этого интервала:
( или ).

Сделаем оценку, применяя уравнение (4) и условие Липшица:

;
.
Поскольку , то разделим на :
.
Возникает противоречие, поскольку при это неравенство не выполняется.

Следовательно, не может иметь отличных от нуля значений. Поэтому . Что и требовалось доказать.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов . Опубликовано: 04-06-2016 Изменено: 20-06-2016