Формулы для решения уравнений 5 класс

Урок 17 Бесплатно Уравнение

Часто приходится описывать реальную ситуацию, процесс, явление с помощью математического языка.

Математический язык- универсальный язык, с помощью него можно однозначно и кратко описать многие закономерности, процессы, задачи и т.д.

Связать реальную жизнь и математическое описание любой ситуации нам позволяет математическая модель.

Описывая реальность с помощью математического языка, люди создают математические модели, превращающие слова в формулы, неравенства, равенства, уравнения и т.п.

Математическая модель дает возможность решать огромное количество практических (природных, технических, научных, экономических, социальных и других) задач.

Математические модели делят на:

• Словесные.
• Графические (схемы, графики, чертежи, рисунки и т.д.).
• Аналитические (алгебраические: числовые равенства, неравенства, уравнения, формулы и т.д.).

На данном уроке подробно рассмотрим одну из аналитических математических моделей- уравнение.

Выясним, что такое уравнение и что называют корнем уравнения.

Рассмотрим простейшие виды уравнений.

Разберем способы и приемы решения уравнений с одним неизвестным.

Рассмотрим алгоритм и примеры решения задач с помощью уравнений.

Уравнения

Часто при решении задач приходится составлять равенства.

Два выражения (числовые или буквенные), соединенные знаком равно «=», образуют равенство.

В математике различают два вида равенств: тождества и уравнения.

Тождества- это числовые равенства, а также равенства, которые выполняются при всех допустимых значениях переменных, входящих в него.

Уравнение- это равенство, содержащее неизвестные числа, обозначенные буквами, значение которых можно определить.

Неизвестное число, входящее в уравнение, называют неизвестным членом уравнения (или просто «неизвестным»).

Чаще всего в математике неизвестные величины обозначают маленькими буквами латинского алфавита x, y, z.

У меня есть дополнительная информация к этой части урока!

Долгое время в математических выкладках не использовали буквенные обозначения и записывали выражения и уравнения словами.

В 1591 году французский ученый философ Франсуа Виет ввел буквенные обозначения. Он предложил использовать гласные буквы латинского алфавита для названия величин, а согласные для неизвестных.

Позже другой французский ученый, философ Рене Декарт предложил иную систему обозначений, связанную с латинскими буквами (которую используют по сегодняшний день).

Для неизвестных было предложено использовать последние буквы латинского алфавита (х, у, z), а для известных величин первые буквы латинского алфавита (а, b, c)

Пример 1:

4 + х = 18 является уравнением с неизвестной х.

12у — 5 = 19 является уравнением с неизвестной у.

(2 + z) — (3 — 1) = 2 является уравнением с неизвестной z.

Все три записи являются равенствами, в каждом из них есть неизвестное число, обозначенное буквой.

Пример 2:

4х — 18 не является уравнением, так как не является равенством.

24 — 5 = 19 не является уравнением, так как не содержит неизвестную.

у + 2 > 12 не является уравнением, так как не является равенством.

Решить уравнение- это значит найти неизвестное число, при котором из уравнения получается верное равенство.

Уравнение считается решенным, если все его решения найдены или доказано, что уравнение решения не имеет.

Значение неизвестного, обращающее уравнение в верное равенство, называют корнем уравнения.

Следовательно, если в уравнение вместо неизвестной подставить ее численное значение и получится верное числовое равенство, то это значение неизвестной будет решением этого уравнения.

Дано уравнение 12 — х + 3 = 10.

1) Пусть х равно 6, получаем

12 — 6 + 3 = 10

9 ≠ 10 (девять не равно десяти)

При подстановке вместо неизвестного число 6, получаем неверное числовое равенство 9 ≠ 10, т.е. число 6 не является корнем уравнения.

2) Пусть х равно 5, получаем

12 — 5 + 3 = 10

10 = 10

При подстановке вместо неизвестного число 5, получаем верное числовое равенство 10 = 10, т.е. число 5 является корнем уравнения.

Уравнение может иметь разное количество корней: существуют уравнения, имеющие один единственный корень, уравнения, имеющие два, три корня.

Встречаются уравнения, вообще не имеющие верного решения, и даже такие уравнения, решением которых являются бесконечное множество решений.

7 — х = 4 уравнение имеет один корень, х = 3, любое другое значение х будет давать неверное равенство.

х = х — 15 уравнение не имеет решения, так как любое значение неизвестного х будет данное равенство обращать в неверное, не существует таких чисел, которые были бы меньше самого себя.

0 ⋅ y = 0 уравнение имеет бесконечное множество верных решений, так как при умножении любого числа на 0, получается 0.

Уравнение, содержащее одну неизвестную, называют уравнением с одной неизвестной.

Уравнения с большим количеством неизвестным называют соответственно уравнением с двумя, тремя и т.д. неизвестными.

Такие уравнения и их решение будете рассматривать в старших классах.

Например, 26 — 2х = 23 — х— это уравнение с одной неизвестной х.

53 — х = 19у— это уравнение с двумя неизвестными х и у.

Любое уравнение имеет левую и правую часть.

Выражение, стоящее слева от знака равно, называют левой частью уравнения, а выражение, которое стоит справа, правой частью уравнения.

Каждый компонент, из которых состоит уравнение, называют членами этого уравнения.

Обычно все члены уравнения, содержащие неизвестное, следует группировать в левой части уравнения, а известные — в правой.

Чаще всего уравнение записывают в левой части страницы, справа делают письменные вычисления (вычислительные операции).

При решении уравнения каждое новое равенство записывается с новой строки (т.е. решение оформляется в виде столбика равенств).

Таким образом, знак равенства при решении уравнения используют только один раз в каждой строке.

Пройти тест и получить оценку можно после входа или регистрации

Формулы для решения уравнений 5 класс

Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.

Сравнение натуральных чисел

Число меньше любого натурального числа.

Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.

Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр

Свойства сложения

Переместительный закон:

Сочетательный закон:

Формула пути

= 50км, = 2ч, = 25км/ч

, 50км = 25км/ч· 2ч

, 25км/ч = 50км : 2ч

, 2ч = 50км : 25км/ч

Корень уравнения

Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.

Что значит «Решить уравнение»

Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.

Правила решения уравнений

• Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

• Чтобы найти неизвестное уменьшаемое, надо к разности при­бавить вычитаемое.

• Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

• Чтобы найти неизвестный множитель, надо произведение раз­делить на известный множитель.

• Чтобы найти неизвестное делимое, надо делитель умножить на частное.

• Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Отрезок, прямая, луч

Отрезок

Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)

Свойство длины отрезка

Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .

Равные отрезки

Два отрезка называют равными, если они совмещаются при наложении.

Свойство прямой

Через две точки проходит только одна прямая.

Измерить отрезок

Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается

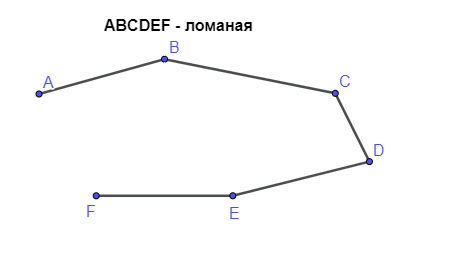
Ломаная

Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом

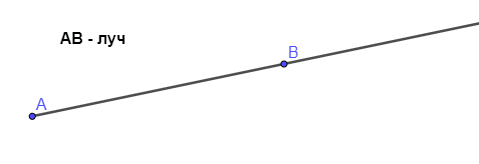
Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.

Угол, биссектриса угла

Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.

Равные углы

Два угла называют равными, если они совмещаются при наложении.

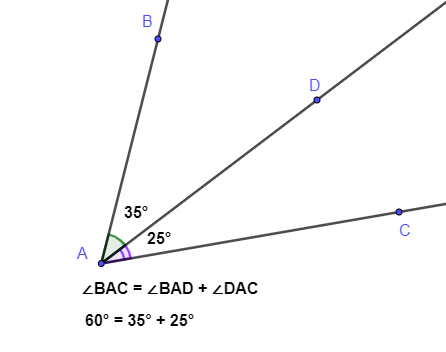
Свойство величины угла

Если между сторонами угла ∠ провести луч , то градусная мера ∠ равна сумме градусных мер углов ∠ и ∠, то есть ∠ = ∠+ ∠.

Биссектриса угла

Луч, который делит угол на два равных угла, называется биссектрисой угла.

Углы: развернутый, прямой, острый, тупой

Развернутый угол

Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.

Прямой угол

Угол, градусная мера которого равна 90°, называют прямым.

Острый угол

Угол, градусная мера которого меньше 90°, называют острым.

Тупой угол

Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.

Многоугольники. Равные фигуры

Равные многоугольники

Два многоугольники называют равными, если они совмещаются при наложении.

Равные фигуры

Две фигуры называют равными, если они совмещаются при наложении.

Треугольники: остроугольный, прямоугольный, тупоугольный

Остроугольный треугольник

Если все углы треугольника острые, то его называют остроугольным треугольником.

Прямоугольный треугольник

Если один из углов треугольника прямой, то его называют прямоугольным треугольником.

Тупоугольный треугольник

Если один из углов треугольника тупой, то его называют тупоугольным треугольником.

Треугольники: равнобедренный, равносторонний, разносторонний

Равнобедренный треугольник

Если две стороны треугольника равны, то его называют равнобедренным треугольником.

Равносторонний треугольник

Если три стороны треугольника равны, то его называют равносторонним треугольником.

Периметр равностороннего треугольника

Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле

Разносторонний треугольник

Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.

Прямоугольник. Квадрат. Периметр

Прямоугольник

Если в четырехугольнике все углы прямые, то его называют прямоугольником.

Свойство прямоугольника

Противоположные стороны прямоугольника равны.

Периметр прямоугольника

Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле

Квадрат

Прямоугольник, у которого все стороны равны, называют квадратом.

Периметр квадрата

Если сторона квадрата равна , то его периметр вычисляют по формуле .

Умножение. Свойства умножения

Умножение

• Произведением числа на натуральное число , которое не равно 1, называют сумму, состоящую из слагаемых, каждый из которых равен . В равенства числа и называют множителями, а число и запись — произведением.

• Если один из двух множителей равен 1, то произведение равно второму множителю.

• Если один из множителей равен нулю, то произведение равно нулю.

• Если произведение равно нулю, то хотя бы один из множителей равен нулю.

Свойства умножения

• Переместительный закон умножения:

• Сочетательный закон умножения:

• Распределительное свойство умножения относительно сложения:

• Распределительное свойство умножения относительно вычитания:

Деление. Деление с остатком

Деление

Для натуральных чисел равенство является правильным, если является правильным равенство

В равенстве число называют делимым, число — делителем, число и запись — частным от деления, отношением, долей.

На ноль делить нельзя.

Для любого натурального числа правильными являются равенства:

,

Деление с остатком

, где — делимое, — делитель, — неполное частное, — остаток, .

Если остаток равен нулю, то говорят, что число делится нацело на число .

Площадь. Площадь квадрата, прямоугольника

Свойства площади фигуры

Равные фигуры имеют равные площади;

Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Площадь прямоугольника

Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.

Площадь квадрата

,

где — площадь квадрата, — длина его стороны.

Объем. Объем прямоугольного параллелепипеда, куба

Свойства объема фигуры

Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.

Объем прямоугольного параллелепипеда

• ,

где — объем параллелепипеда, , и — его измерения, выраженные в одних и тех же единицах;

, где — площадь поверхности прямоугольного параллелепипеда.

• ,

где — площадь основания параллелепипеда, — его высота.

Объем куба

,

где — объем куба, — длина его ребра.

Дроби: правильная, неправильная, сравнение дробей

Правильная дробь

Дробь, числитель которой меньше знаменателя, называют правильной

Неправильная дробь

Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.

Сравнение дробей

• Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.

• Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.

• Все правильные дроби меньше единицы, а неправильные — больше или равны единице.

• Любая неправильная дробь больше любой правильной дроби.

Сложение и вычитание дробей с одинаковыми знаменателями

• Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.

• Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.

Сложение и вычитание смешанных чисел

• Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.

• Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.

Преобразование неправильной дроби в смешанное число

Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно

• числитель разделить на знаменатель;
• полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.

Преобразование смешанного числа в неправильную дробь

Чтобы преобразовать смешанное число в неправильную дробь нужно

• целую часть числа умножить на знаменатель дробной части;
• к полученному произведению прибавить числитель дробной части;
• эту сумму записать как числитель неправильной дроби;
• в его знаменателе записать знаменатель дробной части смешанного числа.

Десятичные дроби: свойства, сравнение, округление

Свойства десятичной дроби

Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.

Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.

Сравнение десятичных дробей

Из двух десятичных дробей больше та, у которой целая часть больше.

Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо

• с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
• после чего сравнить полученные дроби поразрядно.

Округление десятичных дробей

Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо

• все следующие за этим разрядом цифры отбросить.
• если при этом первая из цифр, которые отбрасывают равна 0,1, 2, 3, 4 , то последнюю из цифр, которые оставляют, не меняют ;
• если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8, 9 , то последнюю из цифр, которые оставляют, увеличивают на единицу.

Десятичные дроби: сложение, вычитание

Сложение десятичных дробей

Чтобы найти сумму двух десятичных дробей, нужно:

• уравнять количество цифр после запятых;
• записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
• сложить полученные числа так, как складывают натуральные числа;
• поставить в полученной сумме запятую под запятыми.

Вычитание десятичных дробей

Чтобы найти разность двух десятичных дробей, нужно:

• уравнять количество цифр после запятых;
• записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
• выполнить вычитание так, как вычитают натуральные числа;
• поставить в полученной разности запятую под запятыми.

Десятичные дроби: умножение, деление

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, надо:

• перемножить их как натуральные числа, не обращая внимания на запятые;
• в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.

Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.

Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.

Деление десятичных дробей

Чтобы разделить десятичную дробь на десятичную, надо:

• перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
• выполнить деление на натуральное число.

Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.

Среднее арифметическое

Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.

Найти среднее арифметическое чисел 15, 25 и 20.

15 + 25 + 20 ⏞ с у м м а ч и с е л 3 ⏟ к о л и ч е с т в о ч и с е л = 60 3 = 20

Примечание:

Задача. Автомобиль 200 км ехал со скоростью 50 км/ч. Затем 120 км он ехал со скоростью 30 км/ч. Найти среднюю скорость.

V с р е д н я я = S о б щ t о б щ .

1) 200 + 120 = 320(км) -весь путь;

2) 200 : 50 = 4(ч) — время, затраченное на 1-ую часть пути;

3) 120 : 30 = 4(ч) — время, затраченное на 2-ую часть пути;

4) 4 + 4 = 8(ч) — все время;

5) 320 : 8 = 40(км/ч) — средняя скорость.

Процент

Процентом называют сотую часть величины или числа 1%=

Основные правила математики с примерами. 5 класс: 22 комментария

Спасибо большое! Я решил вспомнить материал по математике и вы мне с этим помогли

Уважаемая Наталья Владимировна! По структуре и подаче материала — это лучшее, что мне удалось найти на просторах интернета. Спасибо вам за труд!

Пожалуйста! Я очень рада, что Вы высоко оценили мой труд.

Спасибо огромное ! У меня завтра впр , и я надеюсь я получу 5 😇💖

Формулы для решения линейных уравнений (математика, 5 класс)

Очень часто необходимо находить корни равенств с неизвестными на уроках математики в 5 классе. Формулы уравнений линейного типа применяются как раз для этих целей. Для их решения нужно следовать некоторой методике, которая называется алгоритмом. Однако для этого нужен определенный «багаж» знаний, включающий приведение подобных компонентов и упрощение выражения.

Общие сведения

Большая часть учебников по математике для 5 класса содержит минимальное количество материала по линейным уравнениям, поскольку тема является несложной. Однако у некоторых учеников, которые не понимают материал или пропустили занятие в школе по какой-либо причине, возникают сложности.

Уравнение — это равенство с неизвестной величиной, принимающей значения, которые удовлетворяют искомому выражению. Иными словами, существует тождество: «2x=8». Оно состоит из константы «2» при переменной «x» и результата выполнения математической операции.

Следует отметить, что «2x» — неизвестная величина, а «8» — известная (ее еще называют постоянной. или константой).

Линейным считается уравнение вида: Ax+B=C, где A — константа при переменной «x», B и C — известные величины. Однако некоторые типы тождеств могут содержать скобки, в которых выполняются операции арифметического типа.

Упрощение выражения — это совокупность математических операций, направленных на уменьшение и оптимизацию тождества. Иными словами, из громоздкого равенства при помощи различных преобразований происходит переход к более простому. Чтобы упростить выражение, необходимо выполнить следующие операции: раскрыть скобки, привести подобные элементы и воспользоваться формулами сокращения величин при нахождении корней уравнения.

Правила раскрытия скобок

В некоторых случаях очередность математических операций сложения и вычитания устанавливается при помощи специальных математических символов для группировки, которые называются скобками. Последние имеют два типа обозначений, а именно: «()» и «[]».

Основные формулы раскрытия скобок:

1. Умножение элемента на сумму (разность) эквивалентно сумме (разности) его произведения на каждый компонент: s*(w+v) = s*w+s*v и s*(w-v) = s*w-s*v, соответственно.
2. Если перед скобкой стоит знак «минус», то величины при этом становятся противоположными числами: -(w-v) = -w-(-v) = -w+v = v-w.
3. Деление суммы (разности) элементов на некоторое число эквивалентно сумме (разности) частных: (w+v)/s = [w/s]+[v/s] и (w-v)/s = [w/s]-[v/s], соответственно.
4. При переносе выражения в другую часть тождества необходимо поменять его знак на противоположный: -(w-v) = 3 или 0 = 3+(w+v).

Четвертое правило используется довольно часто при решении уравнений. При выполнении этой операции многие новички часто делают ошибки, забыв изменить знак на противоположный. Специалисты рекомендуют записать все положения на отдельном листе, положив его перед глазами.

Однако правил раскрытия скобок недостаточно для упрощения выражения с неизвестными величинами. Далее нужно рассмотреть основные положения приведения подобных слагаемых.

Приведение подобных элементов

После раскрытия скобок образуются одинаковые элементы, с которыми можно выполнять различные арифметические операции. Это называется вторым этапом упрощения тождества. Для его применения необходимо знать основные правила работы с одинаковыми элементами уравнения:

1. Величины с противоположными знаками уничтожаются, поскольку в сумме дают ноль: -р+р = 0.
2. Выполнять математические операции сложения и вычитания возможно только с однотипными элементами, т. е. 2x+3x = (2+3)*x. Если компоненты, полученные при раскрытии скобок, не являются однотипными, то их следует записывать отдельно: 2+4x, 4+5x и т. д.
3. Арифметические операции можно производить внутри скобок, т. е. 4*(2x-3x) = 4*(-x).

Следует помнить о переносах компонентов из одной части уравнения в другую, поскольку при этом величина меняет знак на противоположный. Далее следует рассмотреть методику решения линейного уравнения для пятого класса.

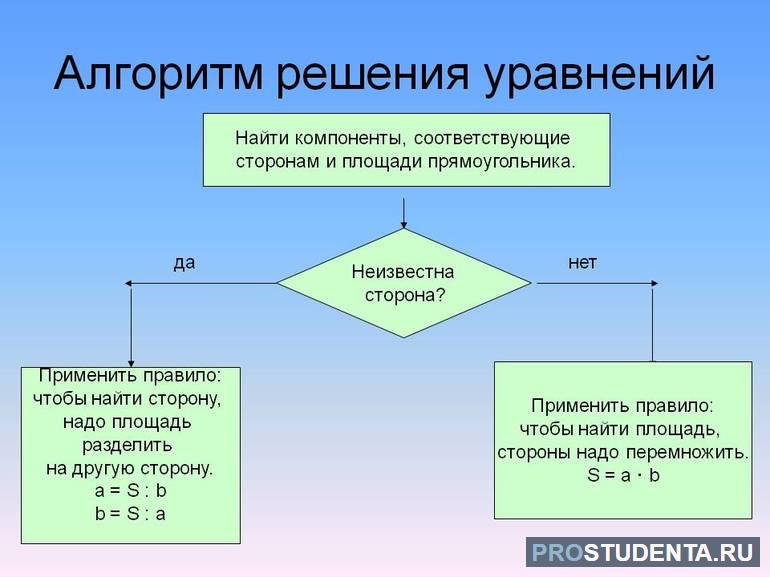
Алгоритм решения задач

При решении любой задачи в математике существует определенная методика, позволяющая легко и быстро найти неизвестные компоненты или параметры. Как правило, результат записывается в буквенной или числовой форме. В первом случае решением является определенное выражение в общем виде. В нем присутствуют цифры и буквы.

Когда в условии необходимо вычислить некоторые параметры, следует подставлять числовые значения в выражения для их нахождения. При решении уравнений линейного вида нужно применить следующий алгоритм:

1. Написать выражение с неизвестным.
2. Раскрыть скобки.
3. Привести общие элементы к единым число-буквенным выражениям.
4. Оставить неизвестные величины в левой части тождества, а константы перенести в правую.
5. Вычислить значение корня по такой формуле: t = M/N, где t — переменная величина, М — коэффициент при неизвестном, N — известное значение.
6. Выполнить проверку, подставив найденную величину переменной в искомое выражение.
7. Записать ответ при верном решении.
8. Если результаты не совпадают, то найти ошибку на одном из шагов.

Необходимо привести пример уравнения по математике для 5 класса и решить его. Нахождение переменной будет выглядеть таким образом:

1. Запись искомого выражения: 4*(x-1)-2*(x-2) = 7*(3-x).
2. Раскрыть скобки: 4x-4−2x+4 = 21−7x.
3. Перенести все элементы влево: 4x-4−2x+4−21+7x = 0.
4. Выполнение операций над одинаковыми компонентами уравнения: 9x-21 = 0.
5. Сортировка элементов: 9x = 21.
6. Определение неизвестной по формуле: x = 21/9 = 2[3/9] = 2[1/3].
7. Проверка: 4*(2[1/3]-1)-2*(2[1/3]-2) = 7*(3−2[1/3]).
8. Расчет и сопоставление результатов: 28/3 = 28/3.
9. Ответ: x = 2[1/3].

Cледует отметить, что проверку проводить необходимо в обязательном порядке. Она позволяет понять, что решение выполнено правильно. Кроме того, постоянно следует упрощать любое выражение, а не делать его длинным и неудобными для нахождения корней.

Однако не во всех случаях предстоит решать легкие задания. Некоторые из них могут быть и сложными, поскольку включают дробные выражения. У дробей следует учитывать знаменатель, предварительно приравняв его к нулевому значению.

Методика работы с дробями

В некоторых случаях линейные уравнения могут иметь вид обыкновенной дроби, в числителе и знаменателе которой находится переменная. Если ее нет, то можно сократить левую и правую части выражения, умножив их на число в знаменателе. Для нахождения корней существует определенный алгоритм решения. Он имеет следующий вид:

1. Записать дробное выражение с неизвестным.
2. Разобрать отдельно числитель и знаменатель.
3. Осуществить операцию по нахождению корня в числителе.
4. Проделать то же самое для знаменателя, приравняв его к нулю.
5. Сопоставить корни. Если один из них превращает знаменатель в ноль, то его не следует учитывать при решении.
6. Выполнить проверку, при которой найденная неизвестная величина должна удовлетворять исходному тождеству.
7. Записать результат, исключив нули знаменателя в виде диапазона или неравенства.

Для реализации алгоритма можно решить пример: [3*(t-2)-(2t+2)]/(5-t) = 0. Нахождение корней выполняется по описанной методике:

1. [3*(t-2)-(2t+2)]/(5-t) = 0.
2. Числитель: 3*(t1−2)-(2t1+2) = 0. Знаменатель: 5-t2 ≠ 0.
3. Раскрыть скобки в числителе: 3t1−6−2t1−2 = 0.
4. Привести подобные компоненты: t1 = 8.
5. В знаменателе переменная не должна принимать величину, эквивалентную 5, т. е. t2 ≠ 5.
6. Сделать проверку для числителя, подставив в искомый числитель: 0 = 0.
7. Записать ответ: t = 8.

Следует отметить, что при решении уравнений такого вида может возникать остаток, полученный при сокращении числителя и знаменателя на одно числовое значение. Этого нужно не допускать, поскольку увеличивается время нахождения корней. Всегда нужно сокращать только на целые значения.

Кроме того, при совпадении корня в числителе и знаменателе уравнение решений не имеет, поскольку превращается в пустое множество. Этого также нельзя допускать. Проверку возможно оптимизировать, воспользовавшись специальным приложением, которое называется онлайн-калькулятором.

Однако специалисты не рекомендуют на начальных этапах обучения увлекаться различным математическим программным обеспечением. В некоторых случаях также придется вспомнить операции с обыкновенными дробями и смешанными числами.

Таким образом, для решения линейных уравнений при помощи формул нужно воспользоваться специальным алгоритмом, который основан на упрощении выражения и выполнении различных арифметических операций с подобными элементами.