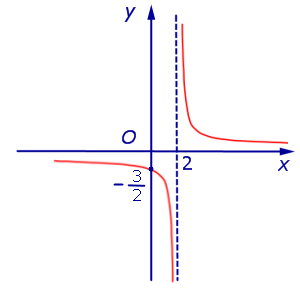
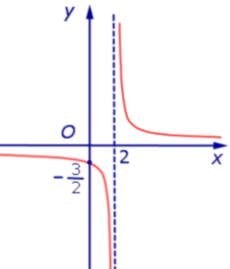
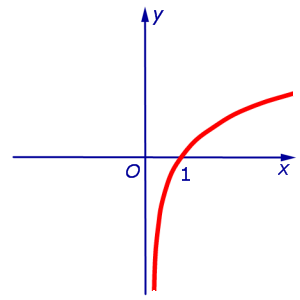
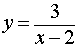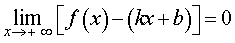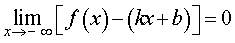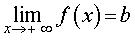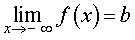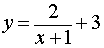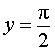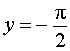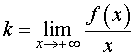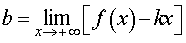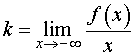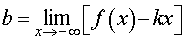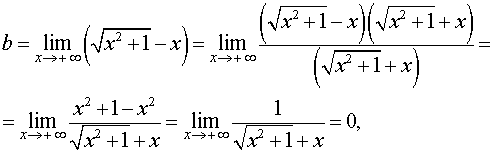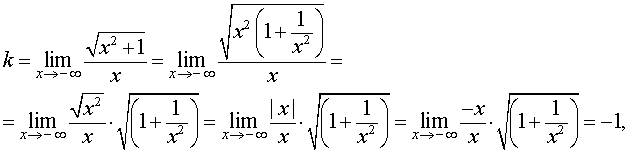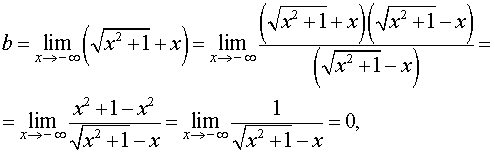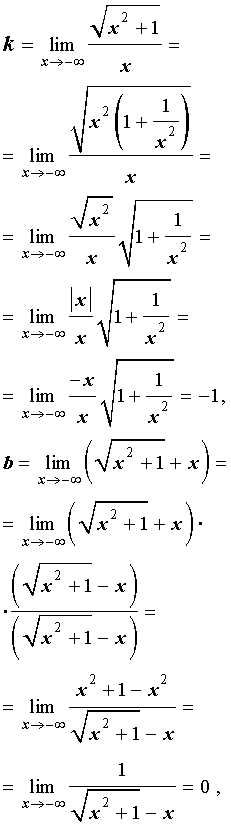Асимптоты
п.1. Понятие асимптоты
Различают вертикальные, горизонтальные и наклонные асимптоты.
Например:
 Вертикальная асимптота x=3 |  Горизонтальная асимптота y=1 |
 Наклонная асимптота y=x | |
п.2. Вертикальная асимптота
Таким образом, практически каждой точке разрыва 2-го рода (см. §40 данного справочника) соответствует вертикальная асимптота.
Вертикальных асимптот может быть сколько угодно, в том числе, бесконечное множество (например, как у тангенса – см. §6 данного справочника).
Например:
Исследуем непрерывность функции \(y=\frac<1><(x-1)(x+3)>\)
ОДЗ: \(x\ne \left\<-3;1\right\>\)
\(\left\
Исследуем \(x_0=-3\). Найдем односторонние пределы: \begin
Точка \(x_0=-3\) — точка разрыва 2-го рода.
Исследуем \(x_1=1\). Найдем односторонние пределы: \begin
Точка \(x_1=1\) — точка разрыва 2-го рода.
Вывод: у функции \(y=\frac<1><(x-1)(x+3)>\) две точки разрыва 2-го рода \(\left\
п.3. Горизонтальная асимптота
Число горизонтальных асимптот не может быть больше двух.
Например:
Исследуем наличие горизонтальных асимптот у функции \(y=\frac<1><(x-1)(x+3)>\)
Ищем предел функции на минус бесконечности: \begin
Ищем предел функции на плюс бесконечности: \begin
Вывод: у функции \(y=\frac<1><(x-1)(x+3)>\) одна горизонтальная асимптота \(y=0\). На плюс и минус бесконечности функция стремится к асимптоте сверху.
Итоговый график асимптотического поведения функции \(y=\frac<1><(x-1)(x+3)>\):
п.4. Наклонная асимптота
Число наклонных асимптот не может быть больше двух.
Чтобы построить график асимптотического поведения, заметим, что у функции \(y=\frac
График асимптотического поведения функции \(y=\frac
п.5. Алгоритм исследования асимптотического поведения функции
На входе: функция \(y=f(x)\)
Шаг 1. Поиск вертикальных асимптот
Исследовать функцию на непрерывность. Если обнаружены точки разрыва 2-го рода, у которых хотя бы один односторонний предел существует и бесконечен, сопоставить каждой такой точке вертикальную асимптоту. Если таких точек не обнаружено, вертикальных асимптот нет.
Шаг 2. Поиск горизонтальных асимптот
Найти пределы функции на плюс и минус бесконечности. Каждому конечному пределу сопоставить горизонтальную асимптоту. Если оба предела конечны и равны, у функции одна горизонтальная асимптота. Если оба предела бесконечны, горизонтальных асимптот нет.
Шаг 3. Поиск наклонных асимптот
Найти пределы отношения функции к аргументу на плюс и минус бесконечности.
Каждому конечному пределу k сопоставить наклонную асимптоту, найти b. Если только один предел конечен, у функции одна наклонная асимптота. Если оба значения k конечны и равны, и оба значения b равны, у функции одна наклонная асимптота. Если оба предела для k бесконечны, наклонных асимптот нет .
На выходе: множество всех асимптот данной функции.
п.6. Примеры
Пример 1. Исследовать асимптотическое поведение функции и построить схематический график:
a) \( y=\frac<4x>
1) Вертикальные асимптоты
Точки, подозрительные на разрыв: \(x=\pm 1\)
Односторонние пределы в точке \(x=-1\) \begin
Односторонние пределы в точке \(x=1\) \begin
Функция имеет две вертикальные асимптоты \(x=\pm 1\)
График асимптотического поведения функции \(y=\frac<4x>
2) Горизонтальные асимптоты
Пределы функции на бесконечности: \begin
График асимптотического поведения функции \(y=e^<\frac<1>
в) \( y=\frac
Заметим, что \( \frac
3) Наклонные асимптоты
Ищем угловые коэффициенты: \begin
Ищем свободный член: \begin
График асимптотического поведения функции \(y=\frac
2) Горизонтальные асимптоты
Пределы функции на бесконечности: \begin
Функция не имеет горизонтальных асимптот.
График асимптотического поведения функции \(y=xe^<\frac<1><2-x>>\)
Асимптоты графика функции
Виды асимптот
Прямая $x=x_<0>$ называется вертикальной асимптотой графика функции $y=f(x)$, если хотя бы одно из предельных значений $\lim _
Замечание. Прямая $x=x_<0>$ не может быть вертикальной асимптотой, если функция непрерывна в точке $x=x_<0>$ . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
Прямая $y=y_<0>$ называется горизонтальной асимптотой графика функции $y=f(x)$, если хотя бы одно из предельных значений $\lim _
Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.
Прямая $y=k x+b$ называется наклонной асимптотой графика функции $y=f(x)$, если $\lim _
Нахождение наклонной асимптоты
(условиях существования наклонной асимптоты)
Если для функции $y=f(x)$ существуют пределы $\lim _
Горизонтальная асимптота является частным случаем наклонной при $k=0$ .
Если при нахождении горизонтальной асимптоты получается, что $\lim _
Кривая $y=f(x)$ может пересекать свою асимптоту, причем неоднократно.
Задание. Найти асимптоты графика функции $y(x)=\frac
Решение. Область определения функции:
$D[f] : x \in(-\infty ;-1) \cup(-1 ;+\infty)$
а) вертикальные асимптоты: прямая $x=-1$ — вертикальная асимптота, так как
то есть, горизонтальных асимптот нет.
в) наклонные асимптоты $y=k x+b$:
Таким образом, наклонная асимптота: $y=x-4$ .
Ответ. Вертикальная асимптота — прямая $x=-1$ .
Асимптоты графиков функций
 Вертикальные асимптоты Вертикальные асимптоты |
 Наклонные асимптоты Наклонные асимптоты |
 Горизонтальные асимптоты как частный случай наклонных асимптот Горизонтальные асимптоты как частный случай наклонных асимптот |
 Поиск наклонных асимптот графиков функций Поиск наклонных асимптот графиков функций |
Вертикальные асимптоты
Во многих разделах нашего справочника приведены графики различных функций. Для многих функций существуют прямые, к которым графики функций неограниченно приближаются. Такие прямые называют асимптотами, и их точное определение мы дадим чуть позже. Как мы увидим далее, асимптоты бывают вертикальными, горизонтальными и наклонными. С вертикальными и горизонтальными асимптотами графика функции мы уже встречались, в частности, в разделе «Гипербола на координатной плоскости. График дробно-линейной функции». С наклонными асимптотами, за исключением горизонтальных, мы пока еще дела не имели.
Определение 1. Говорят, что x стремится к x0 слева и обозначают
Говорят, что x стремится к x0 справа и обозначают
Определение 2. Прямую
называют вертикальной асимптотой графика функции y = f (x) при x , стремящемся к с справа, если функция y = f (x) определена на некотором интервале (с, d) и выполнено соотношение выполнено соотношение
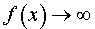
называют вертикальной асимптотой графика функции y = f (x) при x , стремящемся к с слева, если функция y = f (x) определена на некотором интервале (d, c) и выполнено соотношение выполнено соотношение
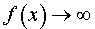
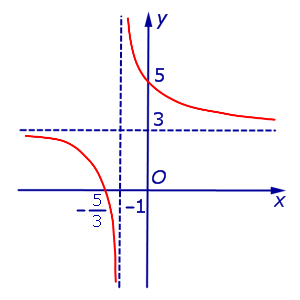
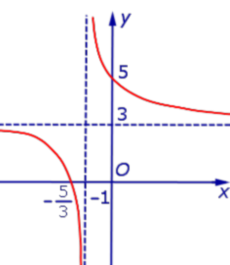
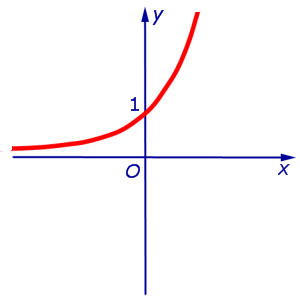
Пример 1. Прямая
является вертикальной асимптотой графика функции
как справа, так и слева (рис. 1)
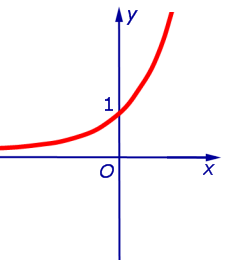
Пример 2. Прямая
является вертикальной асимптотой графика функции
при x , стремящемся к 0 справа (рис. 2)
Наклонные асимптоты
Определение 3. Прямую
называют наклонной асимптотой графика функции y = f (x) при x , стремящемся к 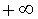
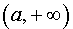
называют наклонной асимптотой графика функции y = f (x) при x , стремящемся к 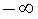
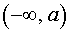
Горизонтальные асимптоты как частный случай наклонных асимптот
Определение 4. Прямую
называют горизотальной асимптотой графика функции y = f (x) при x , стремящемся к 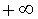
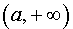
называют горизотальной асимптотой графика функции y f (x) при x , стремящемся к 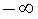
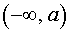
Замечание . Из определений 3 и 5 вытекает, что горизонтальная асимптота является частным случаем наклонной асимптоты y = kx + b, когда угловой коэффициент прямой k = 0 .
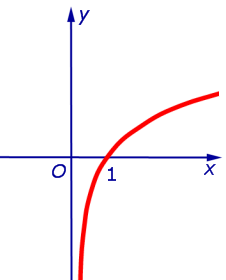
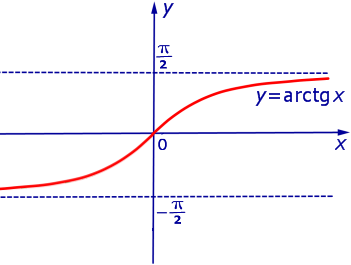
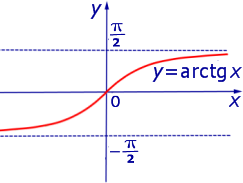
Пример 3. Прямая
является горизонтальной асимптотой графика функции
как при x , стремящемся к 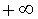
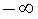
Пример 4. Прямая
является горизонтальной асимптотой графика функции
при x , стремящемся к 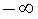
имеет две горизонтальные асимптоты: прямая
является горизонтальной асимптотой графика функции при 
является горизонтальной асимптотой графика функции при 
Поиск наклонных асимптот графиков функций
Для того, чтобы найти наклонную асимптоту графика функции y = f (x) при 

Первая операция. Вычислим предел предел
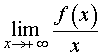 | (1) |
Если предел (1) не существует или существует, но равен существует, но равен 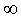

переходим ко второй операции.
Вторая операция. Вычислим предел предел
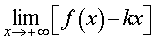 | (2) |
Если предел (2) не существует или существует, но равен существует, но равен 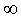

делаем вывод о том, что прямая
является наклонной асимптотой графика функции y = f (x) при 
Совершенно аналогично поступаем для того, чтобы найти наклонную асимптоту графика функции y = f (x) при 

Первая операция. Вычислим предел предел
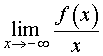 | (3) |
Если предел (3) не существует или существует, но равен существует, но равен 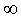

переходим ко второй операции.
Вторая операция. Вычислим предел предел
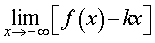 | (4) |
Если предел (4) не существует или существует, но равен существует, но равен 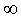

делаем вывод о том, что прямая
является наклонной асимптотой графика функции y = f (x) при 
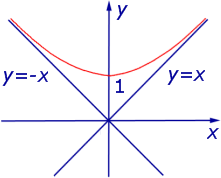
Пример 5. Найти асимптоты графика функции
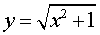 | (5) |
и построить график этой функции.
Решение. Функция (5) определена для всех 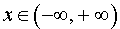
Найдем наклонные асимптоты графика функции (5). При 
Отсюда вытекает, что прямая
– наклонная асимптота графика функции (5) при 
При 
Отсюда вытекает, что прямая
– наклонная асимптота графика функции (5) при 
Итак, y’ > 0 при x > 0 , y’ при x y’ = 0 при x = 0 . Точка x = 0 – стационарная, причем производная функции (5) при переходе через точку x = 0 меняет знак с «–» на «+» . Следовательно, x = 0 – точка минимума функции (5). Других критических точек у функции (5) нет.
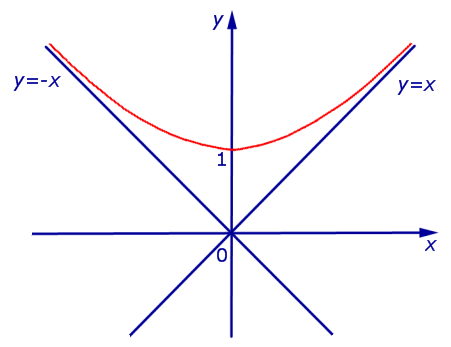
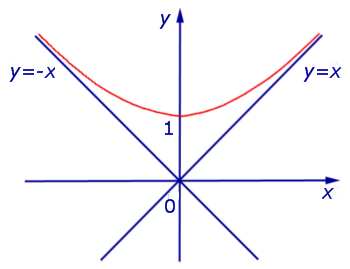
Теперь мы уже можем построить график функции (5):
Заметим, что график функции (5) находится выше асимптот y = x и y =v– x , поскольку справедливо неравенство:
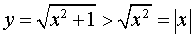
http://www.webmath.ru/poleznoe/formules_8_25.php
http://www.resolventa.ru/spr/matan/asymptote.htm