Формулы тангенса синуса косинуса для тригонометрических уравнений

Основные тригонометрические формулы и тождества sin, cos, tg, ctg

Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.

Основные тождества тригонометрии

Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.

sin 2 a + cos 2 a = 1 t g α = sin α cos α , c t g α = cos α sin α t g α · c t g α = 1 t g 2 α + 1 = 1 cos 2 α , c t g 2 α + 1 = 1 sin 2 α

Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).

Формулы приведения

Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.

sin α + 2 π z = sin α , cos α + 2 π z = cos α t g α + 2 π z = t g α , c t g α + 2 π z = c t g α sin — α + 2 π z = — sin α , cos — α + 2 π z = cos α t g — α + 2 π z = — t g α , c t g — α + 2 π z = — c t g α sin π 2 + α + 2 π z = cos α , cos π 2 + α + 2 π z = — sin α t g π 2 + α + 2 π z = — c t g α , c t g π 2 + α + 2 π z = — t g α sin π 2 — α + 2 π z = cos α , cos π 2 — α + 2 π z = sin α t g π 2 — α + 2 π z = c t g α , c t g π 2 — α + 2 π z = t g α sin π + α + 2 π z = — sin α , cos π + α + 2 π z = — cos α t g π + α + 2 π z = t g α , c t g π + α + 2 π z = c t g α sin π — α + 2 π z = sin α , cos π — α + 2 π z = — cos α t g π — α + 2 π z = — t g α , c t g π — α + 2 π z = — c t g α sin 3 π 2 + α + 2 π z = — cos α , cos 3 π 2 + α + 2 π z = sin α t g 3 π 2 + α + 2 π z = — c t g α , c t g 3 π 2 + α + 2 π z = — t g α sin 3 π 2 — α + 2 π z = — cos α , cos 3 π 2 — α + 2 π z = — sin α t g 3 π 2 — α + 2 π z = c t g α , c t g 3 π 2 — α + 2 π z = t g α

Формулы приведения являются следствием периодичности тригонометрических функций.

Тригонометрические формулы сложения

Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.

Тригонометрические формулы сложения

sin α ± β = sin α · cos β ± cos α · sin β cos α + β = cos α · cos β — sin α · sin β cos α — β = cos α · cos β + sin α · sin β t g α ± β = t g α ± t g β 1 ± t g α · t g β c t g α ± β = — 1 ± c t g α · c t g β c t g α ± c t g β

На основе формул сложения выводятся тригонометрические формулы кратного угла.

Формулы кратного угла: двойного, тройного и т.д.

sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 sin 2 α , cos 2 α = 2 cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α с t g 2 α = с t g 2 α — 1 2 · с t g α sin 3 α = 3 sin α · cos 2 α — sin 3 α , sin 3 α = 3 sin α — 4 sin 3 α cos 3 α = cos 3 α — 3 sin 2 α · cos α , cos 3 α = — 3 cos α + 4 cos 3 α t g 3 α = 3 t g α — t g 3 α 1 — 3 t g 2 α c t g 3 α = c t g 3 α — 3 c t g α 3 c t g 2 α — 1

Формулы половинного угла

Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.

Формулы половинного угла

sin 2 α 2 = 1 — cos α 2 cos 2 α 2 = 1 + cos α 2 t g 2 α 2 = 1 — cos α 1 + cos α c t g 2 α 2 = 1 + cos α 1 — cos α

Формулы понижения степени

sin 2 α = 1 — cos 2 α 2 cos 2 α = 1 + cos 2 α 2 sin 3 α = 3 sin α — sin 3 α 4 cos 3 α = 3 cos α + cos 3 α 4 sin 4 α = 3 — 4 cos 2 α + cos 4 α 8 cos 4 α = 3 + 4 cos 2 α + cos 4 α 8

Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:

Общий вид формул понижения степени

sin n α = C n 2 n 2 n + 1 2 n — 1 ∑ k = 0 n 2 — 1 ( — 1 ) n 2 — k · C k n · cos ( ( n — 2 k ) α ) cos n α = C n 2 n 2 n + 1 2 n — 1 ∑ k = 0 n 2 — 1 C k n · cos ( ( n — 2 k ) α )

sin n α = 1 2 n — 1 ∑ k = 0 n — 1 2 ( — 1 ) n — 1 2 — k · C k n · sin ( ( n — 2 k ) α ) cos n α = 1 2 n — 1 ∑ k = 0 n — 1 2 C k n · cos ( ( n — 2 k ) α )

Сумма и разность тригонометрических функций

Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.

Сумма и разность тригонометрических функций

sin α + sin β = 2 sin α + β 2 · cos α — β 2 sin α — sin β = 2 sin α — β 2 · cos α + β 2 cos α + cos β = 2 cos α + β 2 · cos α — β 2 cos α — cos β = — 2 sin α + β 2 · sin α — β 2 , cos α — cos β = 2 sin α + β 2 · sin β — α 2

Произведение тригонометрических функций

Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.

Формулы произведения тригонометрических функций

sin α · sin β = 1 2 · ( cos ( α — β ) — cos ( α + β ) ) cos α · cos β = 1 2 · ( cos ( α — β ) + cos ( α + β ) ) sin α · cos β = 1 2 · ( sin ( α — β ) + sin ( α + β ) )

Универсальная тригонометрическая подстановка

Все основные тригонометрические функции — синус, косинус, тангенс и котангенс, — могут быть выражены через тангенс половинного угла.

Универсальная тригонометрическая подстановка

sin α = 2 t g α 2 1 + t g 2 α 2 cos α = 1 — t g 2 α 2 1 + t g 2 α 2 t g α = 2 t g α 2 1 — t g 2 α 2 c t g α = 1 — t g 2 α 2 2 t g α 2

Тригонометрические уравнения — формулы, решения, примеры

Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.

Простейшие тригонометрические уравнения

Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.

1. Уравнение `sin x=a`.

При `|a|>1` не имеет решений.

При `|a| \leq 1` имеет бесконечное число решений.

Формула корней: `x=(-1)^n arcsin a + \pi n, n \in Z`

2. Уравнение `cos x=a`

При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.

При `|a| \leq 1` имеет бесконечное множество решений.

Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`

Частные случаи для синуса и косинуса в графиках.

3. Уравнение `tg x=a`

Имеет бесконечное множество решений при любых значениях `a`.

Формула корней: `x=arctg a + \pi n, n \in Z`

4. Уравнение `ctg x=a`

Также имеет бесконечное множество решений при любых значениях `a`.

Формула корней: `x=arcctg a + \pi n, n \in Z`

Формулы корней тригонометрических уравнений в таблице

Для синуса:Для косинуса:Для тангенса и котангенса:Формулы решения уравнений, содержащих обратные тригонометрические функции:

Методы решения тригонометрических уравнений

Решение любого тригонометрического уравнения состоит из двух этапов:

• с помощью тригонометрических формул преобразовать его до простейшего;
• решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.

Рассмотрим на примерах основные методы решения.

Алгебраический метод.

В этом методе делается замена переменной и ее подстановка в равенство.

Пример. Решить уравнение: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 — x)+1=0`

Решение. Используя формулы приведения, имеем:

`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,

делаем замену: `cos(x+\frac \pi 6)=y`, тогда `2y^2-3y+1=0`,

находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:

1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.

2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

Ответ: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

Разложение на множители.

Пример. Решить уравнение: `sin x+cos x=1`.

Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя формулы двойного угла, преобразуем и разложим на множители левую часть:

`sin x — 2sin^2 x/2=0`,

`2sin x/2 cos x/2-2sin^2 x/2=0`,

`2sin x/2 (cos x/2-sin x/2)=0`,

1. `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
2. `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n`, `x_2=\pi/2+ 2\pi n`.

Ответ: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.

Приведение к однородному уравнению

Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:

`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).

Потом разделить обе части на `cos x \ne 0` — для первого случая, и на `cos^2 x \ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.

Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.

Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:

`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,

`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`

`sin^2 x+sin x cos x — 2 cos^2 x=0`.

Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x \ne 0`, получим:

`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда:

1. `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
2. `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.

Ответ. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.

Переход к половинному углу

Пример. Решить уравнение: `11 sin x — 2 cos x = 10`.

Решение. Применим формулы двойного угла, в результате: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^2 x/2`

`4 tg^2 x/2 — 11 tg x/2 +6=0`

Применив описанный выше алгебраический метод, получим:

1. `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
2. `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Ответ. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Введение вспомогательного угла

В тригонометрическом уравнении `a sin x + b cos x =c`, где a,b,c — коэффициенты, а x — переменная, разделим обе части на `sqrt `:

Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: `\frac a>=cos \varphi`, ` \frac b> =sin \varphi`, `\frac c>=C`, тогда:

`cos \varphi sin x + sin \varphi cos x =C`.

Подробнее рассмотрим на следующем примере:

Пример. Решить уравнение: `3 sin x+4 cos x=2`.

Решение. Разделим обе части равенства на `sqrt <3^2+4^2>`, получим:

`3/5 sin x+4/5 cos x=2/5`.

Обозначим `3/5 = cos \varphi` , `4/5=sin \varphi`. Так как `sin \varphi>0`, `cos \varphi>0`, то в качестве вспомогательного угла возьмем `\varphi=arcsin 4/5`. Тогда наше равенство запишем в виде:

`cos \varphi sin x+sin \varphi cos x=2/5`

Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:

`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,

`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

Ответ. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

Дробно-рациональные тригонометрические уравнения

Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.

Пример. Решить уравнение. `\frac <1+cos x>=1-cos x`.

Решение. Умножим и разделим правую часть равенства на `(1+cos x)`. В результате получим:

Учитывая, что знаменатель равным быть нулю не может, получим `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.

Приравняем к нулю числитель дроби: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.

1. `sin x=0`, `x=\pi n`, `n \in Z`
2. `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.

Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.

Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.

Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!

Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.

Тригонометрические формулы. Их вывод

Наиболее часто встречающиеся тригонометрические формулы:

\(\blacktriangleright\) Основные тождества: \[\begin <|l|l|>\hline \sin^2 \alpha+\cos^2 \alpha =1& \mathrm\, \alpha \cdot \mathrm\, \alpha =1 \\ &(\sin\alpha\ne 0, \cos\alpha\ne 0)\\[0.5ex] \hline &\\ \mathrm\, \alpha=\dfrac<\sin \alpha> <\cos \alpha>&\mathrm\, \alpha =\dfrac<\cos \alpha> <\sin \alpha>\\&\\ 1+\mathrm^2\, \alpha =\dfrac1 <\cos^2 \alpha>& 1+\mathrm^2\, \alpha=\dfrac1<\sin^2 \alpha>\\&\\ (\cos\alpha\ne 0)& (\sin\alpha\ne 0) \\ \hline \end\]

\(\blacktriangleright\) Формулы сложения углов: \[\begin <|l|r|>\hline &\\ \sin<(\alpha\pm \beta)>=\sin\alpha\cdot \cos\beta\pm \sin\beta\cdot \cos\alpha & \cos<(\alpha\pm \beta)>=\cos\alpha\cdot \cos\beta \mp \sin\alpha\cdot \sin\beta\\ &\\ \hline &\\ \mathrm\, (\alpha\pm \beta)=\dfrac<\mathrm\, \alpha\pm \mathrm\, \beta><1 \mp \mathrm\, \alpha\cdot \mathrm\, \beta> & \mathrm\, (\alpha\pm\beta)=-\dfrac<1\mp \mathrm\, \alpha\cdot \mathrm\, \beta><\mathrm\, \alpha\pm \mathrm\, \beta>\\&\\ \cos\alpha\cos\beta\ne 0&\sin\alpha\sin\beta\ne 0\\ \hline \end\]

\(\blacktriangleright\) Формулы двойного и тройного углов: \[\begin <|lc|cr|>\hline \sin <2\alpha>=2\sin \alpha\cos \alpha & \qquad &\qquad & \cos<2\alpha>=\cos^2\alpha -\sin^2\alpha\\ \sin \alpha\cos \alpha =\dfrac12\sin <2\alpha>&& & \cos<2\alpha>=2\cos^2\alpha -1\\ & & & \cos<2\alpha>=1-2\sin^2 \alpha\\ \hline &&&\\ \mathrm\, 2\alpha = \dfrac<2\mathrm\, \alpha><1-\mathrm^2\, \alpha> && & \mathrm\, 2\alpha = \dfrac<\mathrm^2\, \alpha-1><2\mathrm\, \alpha>\\&&&\\ \cos\alpha\ne 0, \ \cos2\alpha\ne 0 &&& \sin\alpha\ne 0, \ \sin2\alpha\ne 0\\ \hline &&&\\ \sin <3\alpha>=3\sin \alpha -4\sin^3\alpha && & \cos<3\alpha>=4\cos^3\alpha -3\cos \alpha\\&&&\\ \hline \end\]

\(\blacktriangleright\) Формулы понижения степени: \[\begin <|lc|cr|>\hline &&&\\ \sin^2\alpha=\dfrac<1-\cos<2\alpha>>2 &&& \cos^2\alpha=\dfrac<1+\cos<2\alpha>>2\\&&&\\ \hline \end\]

\(\blacktriangleright\) Формулы произведения функций: \[\begin <|c|>\hline \\ \sin\alpha\sin\beta=\dfrac12\bigg(\cos<(\alpha-\beta)>-\cos<(\alpha+\beta)>\bigg)\\\\ \cos\alpha\cos\beta=\dfrac12\bigg(\cos<(\alpha-\beta)>+\cos<(\alpha+\beta)>\bigg)\\\\ \sin\alpha\cos\beta=\dfrac12\bigg(\sin<(\alpha-\beta)>+\sin<(\alpha+\beta)>\bigg)\\\\ \hline \end\]

\(\blacktriangleright\) Выражение синуса и косинуса через тангенс половинного угла: \[\begin <|l|r|>\hline &\\ \sin<2\alpha>=\dfrac<2\mathrm\, \alpha><1+\mathrm^2\, \alpha> & \cos<2\alpha>=\dfrac<1-\mathrm^2\, \alpha><1+\mathrm^2\, \alpha>\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end\]

\(\blacktriangleright\) Формула вспомогательного аргумента: \[\begin <|c|>\hline \text<Частный случай>\\ \hline \\ \sin\alpha\pm \cos\alpha=\sqrt2\cdot \sin<\left(\alpha\pm \dfrac<\pi>4\right)>\\\\ \sqrt3\sin\alpha\pm \cos\alpha=2\sin<\left(\alpha\pm \dfrac<\pi>6\right)>\\\\ \sin\alpha\pm \sqrt3\cos\alpha=2\sin<\left(x\pm \dfrac<\pi>3\right)>\\\\ \hline \text<Общий случай>\\ \hline\\ a\sin\alpha\pm b\cos\alpha=\sqrt\cdot \sin<(\alpha\pm \phi)>, \ \ \cos\phi=\dfrac a<\sqrt>, \ \sin\phi=\dfrac b<\sqrt>\\\\ \hline \end\]

Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.

Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.

\(\blacktriangleright\) Вывод формулы косинуса разности углов \(\cos<(\alpha -\beta)>=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)

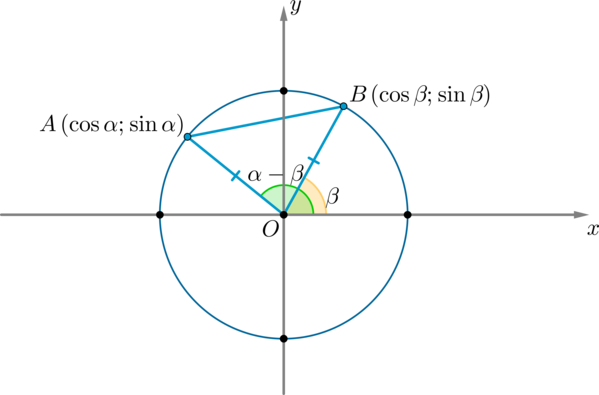
Рассмотрим тригонометрическую окружность и на ней углы \(\alpha\) и \(\beta\) . Пусть этим углам соответствуют точки \(A\) и \(B\) соответственно. Тогда координаты этих точек: \(A(\cos\alpha;\sin\alpha), \ B(\cos\beta;\sin\beta)\) .

Рассмотрим \(\triangle AOB: \ \angle AOB=\alpha-\beta\) . По теореме косинусов:

\(AB^2=AO^2+BO^2-2AO\cdot BO\cdot \cos(\alpha-\beta)=1+1-2\cos(\alpha-\beta) \ (1)\) (т.к. \(AO=BO=R\) – радиус окружности)

По формуле расстояния между двумя точками на плоскости:

Таким образом, сравнивая равенства \((1)\) и \((2)\) :

Отсюда и получается наша формула.

\(\blacktriangleright\) Вывод остальных формул суммы/разности углов:

Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения \(\sin x=\cos(90^\circ-x)\) и \(\cos x=\sin (90^\circ-x)\) :

разделим числитель и знаменатель дроби на \(\cos\alpha\cos\beta\ne 0\)
(при \(\cos\alpha=0 \Rightarrow \mathrm\,(\alpha\pm\beta)=\mp \mathrm\,\beta\) , при \(\cos\beta=0 \Rightarrow \mathrm\,(\alpha\pm\beta)=\pm \mathrm\,\alpha\) ):

Таким образом, данная формула верна только при \(\cos\alpha\cos\beta\ne 0\) .

5) Аналогично, только делением на \(\sin\alpha\sin\beta\ne 0\) , выводится формула котангенса суммы/разности двух углов.

\(\blacktriangleright\) Вывод формул двойного и тройного углов:

Данные формулы выводятся с помощью предыдущих формул:

1) \(\sin 2\alpha=\sin(\alpha+\alpha)=\sin\alpha\cos\alpha+\sin\alpha\cos\alpha=2\sin\alpha\cos\alpha\)

Используя основное тригонометрическое тождество \(\sin^2\alpha+\cos^2\alpha=1\) , получим еще две формулы для косинуса двойного угла:

разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0 \Rightarrow \mathrm\,2\alpha=0\) ):

Таким образом, эта формула верна только при \(\cos\alpha\ne 0\) , а также при \(\cos2\alpha\ne 0\) (чтобы существовал сам \(\mathrm\,2\alpha\) ).

По тем же причинам при \(\sin\alpha\ne 0, \sin2\alpha\ne 0\) .

5) \(\sin3\alpha=\sin(\alpha+2\alpha)=\sin\alpha\cos2\alpha+\cos\alpha\sin2\alpha=\sin\alpha(1-2\sin^2\alpha)+\cos\alpha\cdot 2\sin\alpha\cos\alpha=\)

6) Аналогично выводится, что \(\cos3\alpha=\cos(\alpha+2\alpha)=4\cos^3\alpha-3\cos\alpha\)

\(\blacktriangleright\) Вывод формул понижения степени:

Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:

1) \(\cos2\alpha=2\cos^2\alpha-1 \Rightarrow \cos^2\alpha=\dfrac<1+\cos2\alpha>2\)

2) \(\cos2\alpha=1-2\sin^2\alpha \Rightarrow \sin^2\alpha=\dfrac<1-\cos2\alpha>2\)

Заметим, что в данных формулах степень синуса/косинуса равна \(2\) в левой части, а в правой части степень косинуса равна \(1\) .

\(\blacktriangleright\) Вывод формул произведения функций:

1) Сложим формулы косинуса суммы и косинуса разности двух углов:

Получим: \(\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \Rightarrow \cos\alpha\cos\beta=\dfrac12\Big(\cos(\alpha-\beta)+\cos(\alpha+\beta)\Big)\)

2) Если вычесть из формулы косинуса суммы косинус разности, то получим:

3) Сложим формулы синуса суммы и синуса разности двух углов:

\(\blacktriangleright\) Вывод формул суммы/разности функций:

Обозначим \(\alpha+\beta=x, \alpha-\beta=y\) . Тогда: \(\alpha=\dfrac2, \ \beta=\dfrac2\) . Подставим эти значения в предыдущие три формулы:

Получили формулу суммы косинусов.

Получили формулу разности косинусов.

Получили формулу суммы синусов.

4) Формулу разности синусов можно вывести из формулы суммы синусов:

Аналогично выводится формула суммы котангенсов.

\(\blacktriangleright\) Вывод формул выражения синуса и косинуса через тангенс половинного угла:

(разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0\) и \(\sin2\alpha=0\) ):)

2) Так же, только делением на \(\sin^2\alpha\) , выводится формула для косинуса.

\(\blacktriangleright\) Вывод формул вспомогательного угла:

Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.

Рассмотрим выражение \(a\sin x+b\cos x\) . Домножим и разделим это выражение на \(\sqrt\,\) :

\(a\sin x+b\cos x=\sqrt\left(\dfrac a<\sqrt>\sin x+ \dfrac b<\sqrt>\cos x \right)=\sqrt\big(a_1\sin x+b_1\cos x\big)\)

Заметим, что таким образом мы добились того, что \(a_1^2+b_1^2=1\) , т.к. \(\left(\dfrac a<\sqrt>\right)^2+\left(\dfrac b<\sqrt>\right)^2=\dfrac=1\)

Таким образом, можно утверждать, что существует такой угол \(\phi\) , для которого, например, \(\cos \phi=a_1, \ \sin \phi=b_1\) . Тогда наше выражение примет вид:

\(\sqrt\,\big(\cos \phi \sin x+\sin \phi\cos x\big)=\sqrt\,\sin (x+\phi)\) (по формуле синуса суммы двух углов)

Значит, формула выглядит следующим образом: \[<\large\,\sin (x+\phi),>> \quad \text <где >\cos \phi=\dfrac a<\sqrt>\] Заметим, что мы могли бы, например, принять за \(\cos \phi=b_1, \ \sin \phi=a_1\) и тогда формула выглядела бы как \[a\sin x+b\cos x=\sqrt\,\cos (x-\phi)\]

\(\blacktriangleright\) Рассмотрим некоторые частные случаи формул вспомогательного угла:

\(a) \ \sin x\pm\cos x=\sqrt2\,\left(\dfrac1<\sqrt2>\sin x\pm\dfrac1<\sqrt2>\cos x\right)=\sqrt2\, \sin \left(x\pm\dfrac<\pi>4\right)\)

\(b) \ \sqrt3\sin x\pm\cos x=2\left(\dfrac<\sqrt3>2\sin x\pm \dfrac12\cos x\right)=2\, \sin \left(x\pm\dfrac<\pi>6\right)\)

\(c) \ \sin x\pm\sqrt3\cos x=2\left(\dfrac12\sin x\pm\dfrac<\sqrt3>2\cos x\right)=2\,\sin\left(x\pm\dfrac<\pi>3\right)\)