Формулы тригонометрических уравнений сводящихся к алгебраическим
Методы решения тригонометрических уравнений.
1. Алгебраический метод.
( метод замены переменной и подстановки ).
2. Разложение на множители.
П р и м е р 1. Решить уравнение: sin x + cos x = 1 .
Р е ш е н и е . Перенесём все члены уравнения влево:
sin x + cos x – 1 = 0 ,
преобразуем и разложим на множители выражение в
левой части уравнения:
П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.
Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,
sin x · cos x – sin 2 x = 0 ,
sin x · ( cos x – sin x ) = 0 ,
П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.
Р е ш е н и е . cos 2 x + cos 6 x = 1 + cos 8 x ,
2 cos 4x cos 2x = 2 cos ² 4x ,
cos 4x · ( cos 2x – cos 4x ) = 0 ,
cos 4x · 2 sin 3x · sin x = 0 ,
1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,
3. Приведение к однородному уравнению.
а) перенести все его члены в левую часть;
б) вынести все общие множители за скобки;
в) приравнять все множители и скобки нулю;
г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на
cos ( или sin ) в старшей степени;
д) решить полученное алгебраическое уравнение относительно tan .
П р и м е р . Решить уравнение: 3 sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.
Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,
sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,
tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,
корни этого уравнения: y 1 = — 1, y 2 = — 3, отсюда
1) tan x = –1, 2) tan x = –3,
4. Переход к половинному углу.
П р и м е р . Решить уравнение: 3 sin x – 5 cos x = 7.
Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =
= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,
2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,
tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,
5. Введение вспомогательного угла.
где a , b , c – коэффициенты; x – неизвестное.
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1 . Тогда можно обозначить их соответственно как cos 


6. Преобразование произведения в сумму.
П р и м е р . Решить уравнение: 2 sin x · sin 3 x = cos 4 x .
Р е ш е н и е . Преобразуем левую часть в сумму:
Тригонометрические уравнения — формулы, решения, примеры
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
Простейшие тригонометрические уравнения
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.
1. Уравнение `sin x=a`.
При `|a|>1` не имеет решений.
При `|a| \leq 1` имеет бесконечное число решений.
Формула корней: `x=(-1)^n arcsin a + \pi n, n \in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:


Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью тригонометрических формул преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
Рассмотрим на примерах основные методы решения.
Алгебраический метод.
В этом методе делается замена переменной и ее подстановка в равенство.
Пример. Решить уравнение: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 — x)+1=0`
Решение. Используя формулы приведения, имеем:
`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,
делаем замену: `cos(x+\frac \pi 6)=y`, тогда `2y^2-3y+1=0`,
находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:
1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.
2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Ответ: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Разложение на множители.
Пример. Решить уравнение: `sin x+cos x=1`.
Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя формулы двойного угла, преобразуем и разложим на множители левую часть:
`sin x — 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n`, `x_2=\pi/2+ 2\pi n`.
Ответ: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.
Приведение к однородному уравнению
Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:
`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).
Потом разделить обе части на `cos x \ne 0` — для первого случая, и на `cos^2 x \ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.
Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.
Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`sin^2 x+sin x cos x — 2 cos^2 x=0`.
Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x \ne 0`, получим:
`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда:
- `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
- `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.
Ответ. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.
Переход к половинному углу
Пример. Решить уравнение: `11 sin x — 2 cos x = 10`.
Решение. Применим формулы двойного угла, в результате: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^2 x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Применив описанный выше алгебраический метод, получим:
- `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Ответ. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Введение вспомогательного угла
В тригонометрическом уравнении `a sin x + b cos x =c`, где a,b,c — коэффициенты, а x — переменная, разделим обе части на `sqrt
Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: `\frac a
`cos \varphi sin x + sin \varphi cos x =C`.
Подробнее рассмотрим на следующем примере:
Пример. Решить уравнение: `3 sin x+4 cos x=2`.
Решение. Разделим обе части равенства на `sqrt <3^2+4^2>`, получим:
`3/5 sin x+4/5 cos x=2/5`.
Обозначим `3/5 = cos \varphi` , `4/5=sin \varphi`. Так как `sin \varphi>0`, `cos \varphi>0`, то в качестве вспомогательного угла возьмем `\varphi=arcsin 4/5`. Тогда наше равенство запишем в виде:
`cos \varphi sin x+sin \varphi cos x=2/5`
Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:
`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Ответ. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Дробно-рациональные тригонометрические уравнения
Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.
Пример. Решить уравнение. `\frac
Решение. Умножим и разделим правую часть равенства на `(1+cos x)`. В результате получим:
Учитывая, что знаменатель равным быть нулю не может, получим `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.
Приравняем к нулю числитель дроби: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Решение тригонометрических уравнений, сводящихся к алгебраическим.
- повторить: определение и способы решения простейших тригонометрических уравнений; определение квадратного уравнения, формулы дискриминанта и корней квадратного уравнения
- сформировать знания об отличительных признаках и способах решения тригонометрических уравнений, сводящихся к алгебраическим.
- уметь: выделять среди тригонометрических уравнений тригонометрические уравнения, сводящиеся к алгебраическим и решать их.
Просмотр содержимого документа
«Решение тригонометрических уравнений, сводящихся к алгебраическим.»
Тема урока:
Решение тригонометрических уравнений, сводящихся к алгебраическим.
Цель урока: сформировать представление об алгебраических уравнениях;
познакомить учащихся с методами решения тригонометрических уравнений.
повторить: определение и способы решения простейших тригонометрических уравнений; определение квадратного уравнения, формулы дискриминанта и корней квадратного уравнения
сформировать знания об отличительных признаках и способах решения тригонометрических уравнений, сводящихся к алгебраическим.
уметь: выделять среди тригонометрических уравнений тригонометрические уравнения, сводящиеся к алгебраическим и решать их.
развивать логическое мышление учащихся, память, внимание, речь; умения рассуждать и выделять главное; умение самостоятельно приобретать знания и применять их на практике, развивать навыки самоконтроля и взаимоконтроля.
воспитывать уважительное отношение к одноклассникам, самостоятельность, ответственность, эстетический вкус, аккуратность, интерес к математике.
Оборудование: мультимедийный проектор, экран, лист самооценки.
1. Организационный момент, формирование мотивации работы учащихся (2 мин.)
Здравствуйте, садитесь. Эпиграфом к уроку я взяла такие слова : “Сегодня – мы учимся вместе: я, ваш учитель и вы мои ученики. Но в будущем ученик должен превзойти учителя, иначе в науке не будет прогресса ”. (Сухомлинский Василий Александрович) Структура урока
Проверка домашнего задания 1 мин
Актуализация знаний (работа в парах, фронтальная работа) – 10 мин
II. Основная часть урока
Постановка проблемной ситуации – 1 мин
Изучение нового материала и решение проблемного вопроса – 15 мин
III. Рефлексивно-оценочная часть урока
Закрепление (самостоятельная работа) – 8 мин
Информация о домашнем задании – 2 мин
У каждого есть критерии работы на уроке, задания на урок, оценочный лист. Подпишите его, каждый этап урока вам необходимо оценивать, в конце урока необходимо сдать, оценив свою работу на уроке.
2. Формулирование темы, цели урока.
Решение простейших тригонометрических уравнений. Существуют ли другие типы тригонометрических уравнений? (Да. Если есть «простейшие», то значит, есть более сложные. Исходя из выше сказанного, предлагает сформулировать тему сегодняшнего урока (Решение сложных/других/различных типов тригонометрических уравнений). Тригонометрические уравнения, сводящиеся к алгебраическим (записать дату, тему на доске).
«Величие человека – в его способности мыслить» Блез Паскаль
На столе у каждого из учащихся находятся шаблоны яблок . Написать на «яблоках» свои ожидания от урока. После этого все шаблоны яблок прикрепляются. Получается «Дерево ожиданий».
Как отличить от других?
Кто придумал алгоритм решения?
Сколько корней может быть?
В конце урока проверим сбылись ожидания.
«. Математика — это цепь понятий: выпадет одно звенышко — и не понятно будет дальнейшее» Н.К. Крупская
I. Проверка домашнего задания (Каждый ученик сам оценивает свою работу)
«5»- задание выполнено верно и самостоятельно «4»- задание выполнено верно и полностью, но часть задания выполнена с помощью одноклассников «3»-интересовался решением и все решил с помощью одноклассников. .
sin (x+ 
cos 2 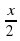
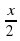
Сколько корней имеет уравнение 2sin 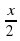
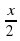
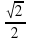
Найдите корень уравнения 
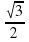
3. Актуализация знаний и подготовка учащихся к активному и сознательному усвоению нового материала (10 мин.).
I Вспомним главное…Фронтальная работа (устно)
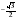
Вычислите: arcsin 0,5; arcсos ( ), arcsin( ); аrcsin 1 ; arcсos (-1); arcsin 0; arcсos1;
arcsin (-1) ; arcсos (-0,5).
Как решить линейное, квадратное, кубическое, биквадратное уравнения?
Дайте определение тригонометрического уравнения.
Сколько корней может иметь тригонометрическое уравнение?
Какое уравнение называется простейшим?
Назовите решение простейших уравнений?
Какие способы решения тригонометрических уравнений вы знаете?
Основное тригонометрическое тождество.
II.Самостоятельная работа (Кодирование «Уравнение — корни» (Работа в тетрадях) 3 минуты
3. sinх = —
4. cosх =
2. х = 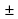
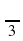
4. х = (-1) n +1 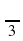
5. х = ± 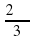
4. cosх = —
6. sinх =
1. x = ± arccos a + 2πn, nϵ Z
2. х = 
3. х = — 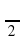
4. х = 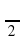
5. х = (-1) n 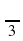
6. х = 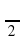
Оценивание: 6 верно решенных примера — оценка «5» 4- 5 – «4» 3 – «3» менее 3 – «2»
III. В каждом из приведенных примеров сделаны ошибки. Назовите верный ответ и подумайте о причине ошибки. (Решение уравнений в тетрадях или устно) работа в группах
cos x= 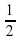
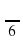
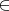
Верно: cos x= 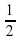
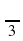
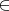
Ошибка в вычислении значений тригонометрической функции
2) sin x =√ 3/2 , x = π/3 + πк, к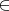
Верно: sin x =√ 3/2 , x = (-1) к π/3 + πк, к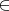
Ошибка в формуле нахождения решения уравнения sin x =a
3) cos x/3 =√ 2/2 , x/3 = ± π/4 + 2 πк ; x = ± 3π/4 + 2 πк/3, к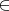
Верно: cos x/3 =√ 2/2 , x/3 = ± π/4 + 2 πк ; x = ± 3π/4 + 6 πк, к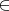
Ошибка в выполнении деления
4) sin 2x =1/3, x = (-1/2) n arcsin1/3 + πn, n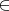
Верно: sin 2x =1/3 , x = (-1) n /2 arcsin1/3 + πn/2, n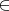
5) cos x = -1/2, x = ±(-π/3) + 2πm, m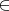
Верно: cos x = -1/2, x = ±2π/3 + 2πm, m 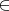
По определению arcсos(-π/3) 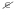
4. Этап усвоения новых знаний и способов действий (15 мин.).
Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важней. Политика существует только для данного момента, а уравнения будут существовать вечно. Альберт Эйнштейн
Уметь: различать вид тригонометрического уравнения
Знать: способ решения тригонометрического уравнения.
ПРОБЛЕМА: Как решить любое задание 15, содержащее тригонометрическое уравнение, на предстоящем экзамене?
Решение тригонометрических уравнений, сводящихся к алгебраическим.
Основные методы решения уравнений: применение формул, разложение на множители, введение новой переменной…
Алгоритм решения методом замены уравнений, сводящимся к алгебраическим
1. Привести уравнение к алгебраическому виду относительно одной из тригонометрических функций
2. Обозначить полученную функцию переменной, обозначив ее ограничения
3. Записать и решить полученное алгебраическое уравнение
4. Вернуться к замене
5. Решить простейшее тригонометрическое уравнение
5. РЕШИТЬ УРАВНЕНИЯ:
1. 2sin² x — 3 sin x — 2 = 0
3. 6sin² x + 5 cos2x — 7 = 0
4. Единый государственный экзамен, 2015 Математика, 11 класс 26.03.15 Досрочный Образец варианта
2cos 3 х — cos ² x + 2 cos x -1 = 0
6. Этап первичной проверки понимания изученного (5 мин.)
Работа дифференцированная, каждый уровень сложности заданий представлен в двух вариантах.
I уровень – «3», II уровень – «4», III уровень – «5» в случае полного правильного решения. Работа будет проверена учителем к следующему уроку, отметки будут выставлены за урок.
7. Этап рефлексии и оценивания. Подведение итогов урока (2 мин.).
http://matemonline.com/dh/%D1%82%D1%80%D0%B8%D0%B3%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F/trigonometricheskie-uravnenija/
http://kopilkaurokov.ru/matematika/uroki/rieshieniie_trighonomietrichieskikh_uravnienii_svodiashchikhsia_k_alghiebraichie