Фундаментальная система линейных алгебраических уравнений

Однородные системы линейных алгебраических уравнений. Фундаментальная система решений. Первая часть.

Однородные системы линейных алгебраических уравнений. Нулевое (тривиальное) решение.

Для начала стоит вспомнить, что такое однородные системы линейных алгебраических уравнений. В теме «Система линейных алгебраических уравнений. Основные термины. Матричная форма записи» вопрос классификации систем осуществлялся подробно, здесь же лишь вкратце напомню основные термины. Итак, система линейных алгебраических уравнений (СЛАУ) называется однородной, если все свободные члены этой системы равны нулю. Например, система $\left \ < \begin& 2x_1-3x_2-x_3-x_4=0;\\ & -4x_1+5x_2+3x_4=0. \end \right.$ является однородной, так как все свободные члены этой системы (т.е. числа, стоящие в правых частях равенств) – нули.

Любая однородная СЛАУ имеет хотя бы одно решение – нулевое (его ещё называют тривиальное), в котором все переменные равны нулю. Подставим, например, $x_1=0$, $x_2=0$, $x_3=0$ и $x_4=0$ в записанную выше систему. Получим два верных равенства:

Однако следствие из теоремы Кронекера-Капелли однозначно указывает на то, что если СЛАУ имеет решение, то есть только два варианта. Либо это решение единственно (и тогда СЛАУ называют определённой), либо этих решений бесконечно много (такую СЛАУ именуют неопределённой). Возникает первый вопрос: как выяснить, сколько решений имеет заданная нам однородная СЛАУ? Одно (нулевое) или бесконечность?

Та однородная СЛАУ, которая рассмотрена выше, имеет не только нулевое решение. Подставим, например, $x_1=1$, $x_2=-1$, $x_3=2$ и $x_4=3$:

Мы получили два верных равенства, поэтому $x_1=1$, $x_2=-1$, $x_3=2$, $x_4=3$ – тоже является решением данной СЛАУ. Отсюда, кстати, следует вывод: так как наша СЛАУ имеет более чем одно решение, то эта СЛАУ является неопределенной, т.е. она имеет бесконечное количество решений.

Кстати сказать, чтобы не писать каждый раз выражения вроде «$x_1=1$, $x_2=-1$, $x_3=2$, $x_4=3$», пишут все значения переменных в матрицу-столбец: $\left(\begin 1 \\ -1 \\ 2 \\ 3 \end \right)$. Эту матрицу тоже называют решением СЛАУ.

Теперь можно вернуться к вопросу о количестве решений однородной СЛАУ. Согласно следствию из теоремы Кронекера-Капелли, если $r=n$ ($n$ – количество переменных), то СЛАУ имеет единственное решение. Если же $r < n$, то СЛАУ имеет бесконечное количество решений.

Случай $r=n$ не интересен. Для однородных СЛАУ он означает, что система имеет только нулевое решение. А вот случай $r < n$ представляет особый интерес.

Этот случай уже был рассмотрен в теме «Базисные и свободные переменные. Общее и базисное решения СЛАУ». По сути, однородные СЛАУ – это всего лишь частный случай системы линейных уравнений, поэтому вся терминология (базисные, свободные переменные и т.д.) остаётся в силе.

Что такое базисные и свободные переменные? показать\скрыть

Прежде чем дать определение этим терминам, стоит вспомнить, что означает фраза «ранг матрицы равен $r$». Она означает, что есть хотя бы один минор $r$-го порядка, который не равен нулю. Напомню, что такой минор называется базисным. Базисных миноров может быть несколько. При этом все миноры, порядок которых выше $r$, равны нулю или не существуют. Теперь можно дать следующее определение:

Выбрать $r$ базисных переменных в общем случае можно различными способами. В примерах я покажу наиболее часто используемый способ выбора.

Фундаментальная система решений однородной СЛАУ.

С однородными СЛАУ связано дополнительное понятие – фундаментальная система решений. Дело в том, что если ранг матрицы системы однородной СЛАУ равен $r$, то такая СЛАУ имеет $n-r$ линейно независимых решений: $\varphi_1$, $\varphi_2$. $\varphi_$.

Часто вместо словосочетания «фундаментальная система решений» используют аббревиатуру «ФСР». Если решения $\varphi_1$, $\varphi_2$. $\varphi_$ образуют ФСР, и $X$ – матрица переменных данной СЛАУ, то общее решение СЛАУ можно представить в таком виде:

$$ X=C_1\cdot \varphi_1+C_2\cdot \varphi_2+\ldots+C_\cdot \varphi_, $$

где $C_1$, $C_2$. $C_$ – произвольные постоянные.

Что значит «линейно независимые решения»? показать\скрыть

В данной ситуации под решением понимается матрица-столбец, в которой перечислены значения неизвестных.

Решения $\varphi_1$, $\varphi_2$, $\ldots$, $\varphi_n$ называются линейно зависимыми, если существуют такие константы $\alpha_1,\;\alpha_2,\;\alpha_3,\ldots,\alpha_n$, что выполняется следующее равенство:

$$ \alpha_1\cdot \varphi_1+\alpha_2\cdot \varphi_2+\ldots+\alpha_n\cdot \varphi_n=O $$

при условии, что среди коэффициентов $\alpha_i$ есть хотя бы один, не равный нулю.

Если же указанное выше равенство возможно лишь при условии $\alpha_1=\alpha_2=\ldots=\alpha_n=0$, то система решений называется линейно независимой.

Буква «$O$» в данном определении обозначает нулевую матрицу. Проще всего пояснить это определение на конкретном примере. Давайте рассмотрим ту СЛАУ, о которой шла речь в начале темы. Мы уже проверили, что $\varphi_1=\left(\begin 1 \\-1 \\2 \\3 \end\right)$ – решение данной СЛАУ. Точно так же можно показать, что $\varphi_2=\left(\begin 16 \\ 11 \\ -4 \\ 3 \end\right)$, $\varphi_3=\left(\begin -5 \\ -4 \\ 2 \\ 0 \end\right)$, $\varphi_4=\left(\begin 7 \\ 5 \\ -2 \\ 1\end\right)$ – решения данной системы.

Примем $\alpha_1=-1$, $\alpha_2=0$, $\alpha_3=4$, $\alpha_4=3$. Выясним, чему же равно выражение $\alpha_1\cdot \varphi_1+\alpha_2\cdot \varphi_2+\alpha_3\cdot \varphi_3+\alpha_4\cdot \varphi_4$:

$$ \alpha_1\cdot \varphi_1+\alpha_2\cdot \varphi_2+\alpha_3\cdot \varphi_3+\alpha_4\cdot \varphi_4= -1\cdot \left(\begin 1 \\-1 \\2 \\3 \end\right)+ 0\cdot \left(\begin 16 \\ 11 \\ -4 \\ 3 \end\right)+ 4\cdot \left(\begin -5 \\ -4 \\ 2 \\ 0 \end\right)+ 3\cdot \left(\begin 7 \\ 5 \\ -2 \\ 1\end\right)=\\ =\left(\begin -1+0-20+21\\ 1+0-16+15 \\ -2+0+8-6 \\ -3+0+0+3\end\right)= \left(\begin 0\\ 0\\ 0\\0\end\right). $$

Итак, существуют такие значения констант $\alpha_1$, $\alpha_2$, $\alpha_3$, $\alpha_4$, не все одновременно равные нулю, что выполняется равенство $\alpha_1\cdot \varphi_1+\alpha_2\cdot \varphi_2+\alpha_3\cdot \varphi_3+\alpha_4\cdot \varphi_4=O$. Вывод: совокупность решений $\varphi_1$, $\varphi_2$, $\varphi_3$, $\varphi_4$ – линейно зависима.

Для сравнения: равенство $\alpha_1\cdot \varphi_1+\alpha_2\cdot \varphi_2=O$ возможно лишь при условии $\alpha_1=\alpha_2=0$ (я не буду это доказывать, поверьте на слово 🙂 ). Следовательно, система $\varphi_1$, $\varphi_2$ является линейно независимой.

Если система является неопределённой, указать фундаментальную систему решений.

Итак, мы имеем однородную СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая однородная система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:

$$ \left( \begin 3 & -6 & 9 & 13 & 0 \\ -1 & 2 & 1 & 1 & 0 \\ 1 & -2 & 2 & 3 & 0 \end \right) \rightarrow \left|\begin & \text<поменяем местами первую и третью>\\ & \text<строки, чтобы первым элементом>\\ & \text <первой строки стала единица.>\end\right| \rightarrow \\ \rightarrow\left( \begin 1 & -2 & 2 & 3 & 0\\ -1 & 2 & 1 & 1 & 0 \\ 3 & -6 & 9 & 13 & 0 \end \right) \begin \phantom <0>\\ II+I\\ III-3\cdot I\end \rightarrow \left( \begin 1 & -2 & 2 & 3 & 0\\ 0 & 0 & 3 & 4 & 0 \\ 0 & 0 & 3 & 4 & 0 \end\right) \begin \phantom <0>\\ \phantom<0>\\ III-II\end \rightarrow \\ \rightarrow\left( \begin 1 & -2 & 2 & 3 & 0\\ 0 & 0 & 3 & 4 & 0 \\ 0 & 0 & 0 & 0 & 0 \end\right). $$

Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.

И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $\rang A=\rang\widetilde = 2$.

Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).

Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на «ступеньках». Что это за «ступеньки» показано на рисунке:

На «ступеньках» стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.

В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.

Почему можно принять переменные $x_1$ и $x_3$ в качестве базисных? Для ответа на этот вопрос давайте вспомним, что ранг матрицы системы равен числу $r=2$. Это говорит о том, что все миноры данной матрицы, порядок которых выше 2, либо равны нулю, либо не существуют. Ненулевые миноры есть только среди миноров второго порядка. Выберем какой-либо ненулевой минор второго порядка. Мы можем выбирать его как в исходной матрице системы $A$, т.е. в матрице $\left( \begin 3 & -6 & 9 & 13 \\ -1 & 2 & 1 & 1 \\ 1 & -2 & 2 & 3 \end \right)$, так и в преобразованной матрице системы, т.е. в $\left( \begin 1 & -2 & 2 & 3 \\ 0 & 0 & 3 & 4 \\ 0 & 0 & 0 & 0 \end\right)$. Так как в преобразованной матрице системы побольше нулей, то будем работать именно с нею.

Итак, давайте выберем минор второго порядка, элементы которого находятся на пересечении строк №1 и №2, и столбцов №1 и №2:

$$ M_<2>^<(1)>=\left| \begin 1 & -2 \\ 0 & 0 \end\right|=1\cdot 0-(-2)\cdot 0=0. $$

Вывод: выбранный нами минор второго порядка не является базисным, ибо он равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №2 (он соответствует переменной $x_2$), то пара переменных $x_1$ и $x_2$ не могут быть базисными переменными.

Осуществим вторую попытку, взяв минор второго порядка, элементы которого лежат на пересечении строк №1, №2 и столбцов №2 и №4:

$$ M_<2>^<(2)>=\left| \begin 2 & 3\\ 3 & 4 \end\right|=2\cdot 4-3\cdot 3=-1. $$

Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №2 (он соответствует переменной $x_2$) и столбца №4 (он соответствует переменной $x_4$), то пару переменных $x_2$ и $x_4$ можно принять в качестве базисных.

Сделаем и третью попытку, найдя значение минора, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №3:

Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №3 (он соответствует переменной $x_3$), то пару переменных $x_1$ и $x_3$ можно принять в качестве базисных.

Как видите, выбор базисных переменных не является однозначным. На самом деле количество вариантов выбора не превышает количество размещений из $n$ элементов по $r$, т.е. не больше чем $C_^$.

В рассматриваемом примере в качестве баисных были приняты переменные $x_1$ и $x_3$ – сугубо из соображений удобства дальнейшего решения. В чём это удобство состоит, будет видно чуток позже.

Базисные переменные выбраны: это $x_1$ и $x_3$. Количество свободных переменных, как и количество решений в ФСР, равно $n-r=2$. Свободными переменными будут $x_2$ и $x_4$. Нам нужно выразить базисные переменные через свободные.

Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $\left( \begin 1 & -2 & 2 & 3 & 0\\ 0 & 0 & 3 & 4 & 0 \\ 0 & 0 & 0 & 0 & 0 \end\right)$ от нулевой строки:

$$ \left( \begin 1 & -2 & 2 & 3 & 0\\ 0 & 0 & 3 & 4 & 0 \end\right) $$

Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:

Почему меняются знаки? Что вообще значит это перенесение столбцов? показать\скрыть

Давайте обратимся к расширенной матрице системы, которая после преобразований имеет вид $\left( \begin 1 & -2 & 2 & 3 & 0\\ 0 & 0 & 3 & 4 & 0 \end\right)$. Перейдём от матрицы к уравнениям. Первая строка соответствует уравнению $x_1-2x_2+2x_3+3x_4=0$, а вторая строка соответствует уравнению $3x_3+4x_4=0$. Теперь перенесём свободные переменные $x_2$ и $x_4$ в правые части уравнений. Естественно, что когда мы переносим выражение $4x_4$ в правую часть уравнения, то знак его изменится на противоположный, и в правой части появится $-4x_4$.

Если опять записать полученную систему в виде матрицы, то мы и получим матрицу с перенесёнными за черту столбцами.

А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:

$$ \left( \begin 1 & 2 & 2 & -3\\ 0 & 3 & 0 & -4 \end\right) \begin \phantom <0>\\ II:3 \end \rightarrow \left( \begin 1 & 2 & 2 & -3\\ 0 & 1 & 0 & -4/3 \end\right) \begin I-2\cdot II \\ \phantom <0>\end \rightarrow \\ \rightarrow \left(\begin 1 & 0 & 2 & -1/3\\ 0 & 1 & 0 & -4/3 \end\right). $$

Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Вспоминая, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, получим:

Нами найдено общее решение заданной однородной СЛАУ. Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=2x_2-\frac<1><3>x_4$ и $x_3=-\frac<4><3>x_4$ в левую часть первого уравнения, получим:

$$ 3x_1-6x_2+9x_3+13x_4=3\cdot \left(2x_2-\frac<1><3>x_4\right)-6x_2+9\cdot \left(-\frac<4><3>x_4\right)+13x_4=0. $$

Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.

Теперь найдем фундаментальную систему решений. ФСР будет содержать $n-r=2$ решения. Для нахождения ФСР составим таблицу. В первой строке таблицы будут перечислены переменные: сначала базисные $x_1$, $x_3$, а затем свободные $x_2$ и $x_4$. Всего в таблице будут три строки. Так как у нас 2 свободные переменные, то под свободными переменными запишем единичную матрицу второго порядка, т.е. $\left(\begin 1 & 0 \\0 & 1\end\right)$. Таблица будет выглядеть так:

Теперь будем заполнять свободные ячейки. Начнём со второй строки. Мы знаем, что $x_1=2x_2-\frac<1><3>x_4$ и $x_3=-\frac<4><3>x_4$. Если $x_2=1$, $x_4=0$, то:

Найденные значения $x_1=2$ и $x_3=0$ запишем в соответствующие пустые ячейки второй строки:

Заполним и третью строку. Если $x_2=0$, $x_4=1$, то:

Найденные значения $x_1=-\frac<1><3>$ и $x_3=-\frac<4><3>$ запишем в соответствующие пустые ячейки третьей строки. Таким образом таблица будет заполнена полностью:

Из второй и третьей строки таблицы мы и запишем ФСР. Матрица неизвестных для нашей системы такова: $X=\left(\begin x_1 \\x_2 \\x_3 \\x_4 \end\right)$. В том же порядке, в котором в матрице $X$ перечислены переменные, записываем значения переменных из таблицы в две матрицы:

$$ \varphi_1=\left(\begin 2 \\1 \\0 \\0 \end\right);\; \varphi_2=\left(\begin -1/3 \\0 \\ -4/3 \\1 \end\right). $$

Совокупность $\varphi_1=\left(\begin 2 \\1 \\0 \\0 \end\right)$, $\varphi_2=\left(\begin -1/3 \\0 \\ -4/3 \\1 \end\right)$ и есть ФСР данной системы. Общее решение можно записать теперь так: $X=C_1\cdot \varphi_1+C_2\cdot \varphi_2$. Или в развёрнутом виде:

$$ X=C_1\cdot\left(\begin 2 \\1 \\0 \\0 \end\right)+C_2\cdot\left(\begin -1/3 \\0 \\ -4/3 \\1 \end\right), $$

где $C_1$ и $C_2$ – произвольные постоянные.

Ответ: Общее решение: $\left\ <\begin& x_1=2x_2-\frac<1><3>x_4;\\ & x_2\in R;\\ & x_3=-\frac<4><3>x_4;\\ & x_4 \in R. \end\right.$. Или так: $X=C_1\cdot\left(\begin 2 \\1 \\0 \\0 \end\right)+C_2\cdot\left(\begin -1/3 \\0 \\ -4/3 \\1 \end\right)$, где $C_1$ и $C_2$ – произвольные константы. Фундаментальная система решений: $\varphi_1=\left(\begin 2 \\1 \\0 \\0 \end\right)$, $\varphi_2=\left(\begin -1/3 \\0 \\ -4/3 \\1 \end\right)$.

Записать ФСР однородной СЛАУ

зная общее решение. Записать общее решение с помощью ФСР.

Общее решение уже было получено в теме «метод Крамера» (пример №4). Это решение таково:

Опираясь на предыдущий пример №1, попробуйте составить ФСР самостоятельно, а потом сверить с ответом.

Ранг матрицы системы $r=3$ (поэтому у нас три базисных переменных), количество переменных $n=5$. Количество свободных переменных и количество решений ФСР равно $n-r=2$.

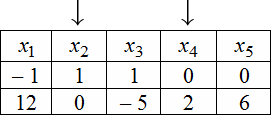
Так же, как и в предыдущем примере, составим ФСР. При составлении учтём, что $x_1$, $x_2$, $x_3$ – базисные переменные, а $x_4$, $x_5$ – свободные переменные.

Совокупность $\varphi_1=\left(\begin -17/19 \\-15/19 \\20/19 \\1\\0 \end\right)$, $\varphi_2=\left(\begin 144/19 \\ 41/19 \\ -4/19\\0\\1 \end\right)$ и есть ФСР данной системы. Общее решение можно записать теперь так: $X=C_1\cdot \varphi_1+C_2\cdot \varphi_2$. Или в развёрнутом виде:

$$ X=C_1\cdot\left(\begin -17/19 \\-15/19 \\20/19 \\1\\0 \end\right)+C_2\cdot\left(\begin 144/19 \\ 41/19 \\ -4/19\\0\\1 \end\right), $$

где $C_1$ и $C_2$ – произвольные постоянные.

Ответ: Фундаментальная система решений: $\varphi_1=\left(\begin -17/19 \\-15/19 \\20/19 \\1\\0 \end\right)$, $\varphi_2=\left(\begin 144/19 \\ 41/19 \\ -4/19\\0\\1 \end\right)$. Общее решение: $X=C_1\cdot\left(\begin -17/19 \\-15/19 \\20/19 \\1\\0 \end\right)+C_2\cdot\left(\begin 144/19 \\ 41/19 \\ -4/19\\0\\1 \end\right)$, где $C_1$ и $C_2$ – произвольные константы.

Продолжение этой темы рассмотрим во второй части, где разберём ещё один пример с нахождением общего решения и ФСР.

Однородные СЛАУ. Фундаментальная система решений

Однородные СЛАУ

Однородной СЛАУ называется система, все правые части которой равны нулю одновременно.

Однородная СЛАУ, записанная в матричном виде, $A X=\Theta$ всегда совместна, так как $X=\Theta$ всегда является ее решением.

Заметим, что если $x_<1>, x_<2>$ — это два решения однородной СЛАУ, то их линейная комбинация также будет решением однородной СЛАУ:

$$Y=\lambda_ <1>x_<1>+\lambda_ <2>x_<2>$$ $$A Y=A\left(\lambda_ <1>x_<1>+\lambda_ <2>x_<2>\right)=\lambda_ <1>A x_<1>+\lambda_ <2>A x_<2>=\lambda_ <1>\Theta+\lambda_ <2>\Theta=\Theta$$

Если однородная квадратная СЛАУ имеет ненулевое решение, то определитель матрицы системы равен нулю.

Задание. Выяснить, имеет ли однородная СЛАУ $\left\<\begin 3 x-2 y=-1 \\ x+3 y=7 \end\right.$ ненулевые решения.

$$\Delta=\left|\begin 3 & -2 \\ 1 & 3 \end\right|=9-(-2)=9+2=11 \neq 0$$

Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$

Ответ. Система имеет только нулевое решение.

Фундаментальная система решений

Рассмотрим множество всех столбцов, которые являются решениями исходной системы.

Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.

Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы. Любое решение исходной системы есть линейная комбинация решений ФСР.

Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и общего решения соответствующей однородной СЛАУ.

Задание. Найти общее решение и ФСР однородной системы $\left\<\begin x_<1>+x_<2>-3 x_<4>-x_<5>=0 \\ x_<1>-x_<2>+2 x_<3>-x_<4>=0 \\ 4 x_<1>-2 x_<2>+6 x_<3>+3 x_<4>-4 x_<5>=0 \\ 2 x_<1>+4 x_<2>-2 x_<3>+4 x_<4>-7 x_<5>=0 \end\right.$

Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):

$$A=\left(\begin 1 & 1 & 0 & -3 & -1 \\ 1 & -2 & 2 & -1 & 0 \\ 4 & -2 & 6 & 3 & -4 \\ 2 & 4 & -2 & 4 & -7 \end\right)$$

с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем первую, от третьей — четыре первых, от четвертой — две первых:

$$A \sim\left(\begin 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & -6 & 6 & 15 & 0 \\ 0 & 2 & -2 & 10 & -5 \end\right)$$

Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три вторых, к четвертой прибавляем вторую:

$$A \sim\left(\begin 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 9 & -3 \\ 0 & 0 & 0 & 12 & -4 \end\right)$$

От четвертой строки отнимем $\frac<4><3>$ третьей и третью строку умножим на $\frac<1><3>$ :

$$A \sim\left(\begin 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 3 & -1 \\ 0 & 0 & 0 & 0 & 0 \end\right)$$

Нулевые строки можно далее не рассматривать, тогда получаем, что

$$A \sim\left(\begin 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 3 & -1 \end\right)$$

Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а ко второй строке прибавляем третью:

$$A \sim\left(\begin 1 & 1 & 0 & -6 & 0 \\ 0 & -2 & 2 & 5 & 0 \\ 0 & 0 & 0 & 3 & -1 \end\right)$$

то есть получаем систему, соответствующую данной матрице:

Или, выразив одни переменные через другие, будем иметь:

Здесь $x_<2>, x_<4>$ — независимые (или свободные) переменные (это те переменные, через которые мы выражаем остальные переменные), $x_<1>, x_<3>, x_<5>$ — зависимые (связанные) переменные (то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от пяти переменных) и ранга матрицы $r$ (в этом случае получили, что $r=3$ — количество ненулевых строк после приведения матрицы к ступенчатому виду): $n-r=5-3=2$

Так как ранг матрицы $r=3$ , а количество неизвестных системы $n=5$ , то тогда количество решений в ФСР $n-r=5-3=2$ (для проверки, это число должно равняться количеству свободных переменных).

Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:

Тогда придавая в первом случае, например, независимым переменным значения $x_<2>=1$ , $x_<4>=0$ получаем, что $\left\<\begin x_<1>=-1+6 \cdot 0=-1 \\ x_<3>=1-\frac<5> <2>\cdot 0=1 \\ x_<5>=3 \cdot 0=0 \end\right.$ . Полученные значения записываем в первую строку таблицы. Аналогично, беря $x_<2>=0$ , $x_<4>=2$, будем иметь, что =12, x_<3>=-5, x_<5>=6> , что и определяет второе решение ФСР. В итоге получаем следующую таблицу:

Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:

$$X_<1>=\left(\begin -1 \\ 1 \\ 1 \\ 0 \\ 0 \end\right), X_<2>=\left(\begin 12 \\ 0 \\ -5 \\ 2 \\ 6 \end\right)$$

Общее решение является линейной комбинацией частных решений:

$$X=C_ <1>X_<1>+C_ <2>X_<2>=C_<1>\left(\begin -1 \\ 1 \\ 1 \\ 0 \\ 0 \end\right)+C_<2>\left(\begin 12 \\ 0 \\ -5 \\ 2 \\ 6 \end\right)$$

где коэффициенты $C_<1>, C_<2>$ не равны нулю одновременно. Или запишем общее решение в таком виде:

Придавая константам $C_<1>, C_<2>$ определенные значения и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.

Фундаментальная система решений СЛАУ

Вы будете перенаправлены на Автор24

Системой линейных уравнений называется система вида: $\begin a_ <11>\cdot x_1 +. + a_ <1n>\cdot x_n = b_1 \\ . \\ a_ \cdot x_1 + a_ \cdot x_n = b_m \end$

Здесь каждая буква относится к своей группе обозначений, $x_1. x_n$ — это неизвестные числа или переменные, подлежащие поиску, $a_11. a_$ — множители, содержащиеся при неизвестных, $b_1. b_m$ — свободные члены таблицы из чисел, получаемой на основе приведённой СЛАУ.

В компактной форме СЛАУ принято записывать в виде формулы вида $A \cdot X = B$. В этой формуле под большой буквой $A$ подразумевается матрица множителей при неизвестных системы, а буквами $X$ и $B$ обозначены вектор-столбец неизвестных системы и свободных членов.

Матрица $A$ называется основной матрицей системы, вот как она будет выглядеть:

$A = \begin a_ <11>& … & a_ <1n>\\ \vdots & … & \vdots \\ a_ & … & a_ \end$, $b=\begin b_1 \\ \vdots \\ b_m \end$

Если через длинную черту после матрицы множителей при неизвестных записан столбец свободных членов, то матрицу называют расширенной матрицей системы.

Необходимая терминология

Решением системы называют такие $n$ значений неизвестных $x_1=c_1, x_2=c_2…x_n-c_n$, что при их использовании все её уравнения становятся верными соблюдающимися равенствами. Найденное решение системы можно записать в виде таблицы неизвестных одним столбцом:

$C= \begin c_1 \\ c_2 \\ \vdots \\ c_n \end$.

В зависимости от количеств групп переменных, подходящих для соблюдения всей системы, различают совместные и несовместные СЛАУ. Объединённая в систему группа равенств называется совместной, если она имеет хотя бы одно решение и несовместной, если она не имеет решений.

Готовые работы на аналогичную тему

Среди первого типа существуют определённые СЛАУ, имеющие только одно решение и неопределённые, под такие подпадают все, которые можно решить с получением больше одного ответа.

Однородные и неоднородные системы линейных уравнений

Система линейных уравнений называется однородной, если все её свободные члены равны нулю. Если в системе хотя бы один из свободных членов ненулевой, то она называется неоднородной, другие же СЛАУ с нулевым $B$ наоборот однородны.

Однородные системы совместны, так как $x_1=x_2=. x_n=0$ будет решением для систем, имеющих особенность в виде нулевого столбца $B$. Иначе такая группа ответов называется нулевым или тривиальным способом решения.

Нетривиальными же называются ответы на СЛАУ, детерминант матрицы которой не $0$. В группе ответов таких систем хотя бы одно из неизвестных подходит под $x_i$ ≠ $0$. Для поиска детерминанта можно воспользоваться $LU$ разложениями, гаусовым методом или его модификацией в виде способа Жордана-Гаусса.

Общее, частное и фундаментальное решения

Частным решением системы называется индивидуальное записанное в одну строчку, тогда как общее $X_o$ записывается через свободные переменные в одну строчку, оно представляет собой некое множество чисел, подходящих под данные условия. Общее $X_o$ включает в себя все индивидуальные.

Фундаментальной же системой решений (ФСР) называется совокупность $(n-r)$ векторов, являющихся линейно независимыми векторами системы. Здесь $r$ — это ранг исследуемой матрицы, согласно теореме Капелли, он равен количеству её основных неизвестных. Найти его можно путём разрешённых преобразований над изучаемым объектом, в частности, можно использовать метод Гаусса или другие.

Фундаментальная система решений частенько представлена как сумма всех возможных решений:

Здесь $С_1, C_2. C_$ — некоторые постоянные.

Приведена пример, в котором все свободные члены ненулевые:

$\begin x_1 – x_2 + x_3-x_4=4 \\ x_1+x_2+2x_3+3x_4=8 \\ 2x_1+4x_2+5x_3+10x_4=20 \\ 2x_1-4x_2+x_3-6x_4=4\\ \end$.

Ранг всех матриц соответсвует двойке, рассчитаем базисный минор:

Избавимся от двух нижних равенств из примера и получим:

$\begin x_1 – x_2=4-c_3+c_4 \\ x_1+x_2=8-2c_3-3c_4 \\ \end$

Общим решением системы будет строчка $(6-\frac<3><2>c_3-c_4; 2-\frac<1><2>c_3-2c_4;c_3; c_4)$.

Теперь посмотрим, что буде в случае с нулевым столбцом за чертой:

$\begin x_1 – x_2 + x_3-x_4=0 \\ x_1+x_2+2x_3+3x_4=0 \\ 2x_1+4x_2+5x_3+10x_4=0 \\ 2x_1-4x_2+x_3-6x_4=0 \end$.

Ранг также соответствует двойке, а её решениями будут

$c_1=-\frac<3> <2>c_3-c_4; c_2=-\frac<1><2>c_3-2c_4$. Константы же $c_3$ и $c_4$ выберем любые, например, возьмём их равными $c_3=0;c_4=1$.

Итак, используя приведённые выше значения $c_3=0;c_4=1$:

Фундаментальное решение системы можно записать так:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 17 04 2021