Фундаментальная система решений линейного однородного дифференциального уравнения
Высшая математика
Рассмотрим линейное однородное дифференциальное уравнение
Фундаментальной системой решений однородного линейного дифференциального уравнения называется упорядоченный набор из n линейно независимых решений уравнения.
Доказано, что у однородного линейного дифференциального уравнения с непрерывными коэффициентами существует фундаментальная система решений.
И пусть функции y 1 ( x ), y 2( x ). y n( x ) — решения линейного однородного уравнения с начальными условиями:
Фундаментальная система решений линейного однородного уравнения
Определение. Любые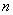 
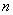
линейно независимых решений линейного однородного дифференциального уравнения -ного порядка называется фундаментальной системой решений этого уравнения.
Из предыдущих теорем сразу следует еще одна важная теорема.
Теорема 7. Решения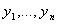 
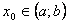
уравнения (2) образуют фундаментальную систему решений этого уравнения тогда и только тогда, когда их определитель Вронского 
отличен от 0 хотя бы в одной точке 
.
Доказательство. Равносильная переформулировка утверждения теоремы – решения 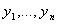линейно зависимы тогда и только тогда, когда 
на 
. Но это утверждение сразу следует из теорем 5 и 6.
Теорема 8. Для любого линейного однородного дифференциального уравнения (2) существует фундаментальная система его решений.
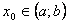
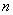
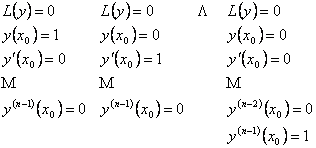
Доказательство. Построим такую фундаментальную систему решений. Для этого возьмем произвольную точку и поставим различных задач Коши: 
.
По теореме 1 о существовании и единственности у каждой из этих задач имеется решение, и мы обозначим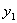 
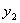
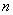
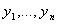
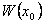
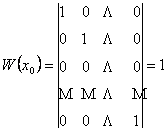
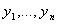
— решение 1-й задачи, 
— решение 2-й задачи, …, 
— решение -ной задачи. Мы получили — решения уравнения (2). Найдем 
для этих функций: 
. Следовательно, по теореме 7, функции образуют искомую фундаментальную систему решений уравнения (2).
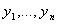
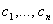
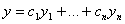
Теорема 9. Пусть — фундаментальная система решений уравнения (2). Тогда для любого решения 
этого уравнения существуют постоянные 
такие, что 
.
Доказательство. Возьмем произвольную точку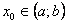 
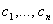
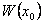
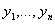
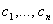
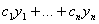
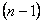
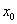
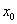
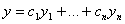
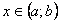
и рассмотрим систему уравнений относительно неизвестных : 
(11). Определитель этой системы 
не равен 0, т.к. 
— фундаментальная система решений. Поэтому у нее существует (и притом единственное) решение . Рассмотрим теперь функцию 
. По теореме 2 она является решением уравнения (2). Ввиду равенств (11) значения этой функции и ее производных до порядка 
включительно в точке 
совпадают со значениями и ее последовательных производных в точке . По теореме 1 о единственности решения задачи Коши , 
.
Замечание. Теоремы 8 и 9 означают, что размерность векторного пространства решений уравнения (2) равна 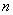, а любая фундаментальная система решений представляет собой базис этого пространства
Система линейных уравнений. Теорема Кронекера-Капелли без доказательства.
Системой линейных алебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида
, где чила 
, 
, 
называются коэффициентами системы, числа 
— свободными членами. Системы лу удобно записывать в виде матрицы.
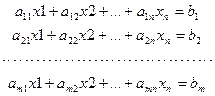
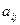
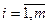
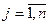
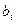
Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Совместная система называется определённой, если она имеет единственное решение, и неопределённой, если имеет более одного решения. Частным решением системы называется каждое решение неопределённой системы. Общим решением называется совокупность всех частных решений системы. Система лу называется однородной, если все свободные члены равны нулю. Тривиальным называется решение, когда все неизвестные раны нулю.
Теорема: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.
Теоремы: Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Если ранг совместной матрицы меньше числа неизвестных, то система имеет бесчисленное множество решений. Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг её основной матрицы был меньше числа неизвестных. Для того, чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и лостаточно, чтобы её определитель был равен нулю.
Векторы, линейные операции над векторами, их свойства.
Вектор – направленный отрезок, который можно передвигать параллельно самому себе.
Два вектора называются равными, если при параллельном переносе, совмещающим начала, совмещаются и концы.
Модулем вектора называется длина вектора (равная корню из суммы квадратов координат). Если модуль вектора равен 1, то вектор единичный.
Два вектора называются коллинеарными, если они лежат на параллельных или совпадающих прямых.
Три вектора называются компланарными, если при их параллельном переносе, совмещающим начала, они оказываются лежащими в одной плоскости.
Углом между двумя векторами называется угол, полученный при параллельном переносе векторов в общее начало.
ω=0– векторы сонаправлены ω=p — противонаправлены ω=p/2 – перпендикулярны
Суммой двух векторов является вектор идущий из начала первого вектора в конец второго, если конец первого и начало второго совмещены параллельным переносом.
Суммой двух векторов называется вектор, являющийся диагональю в параллелограмме, стороны которого образованны параллельным переносом векторов в общее начало, и исходящий из точки совмещения.
Разностью двух векторов является вектор идущий из конца второго вектора в конец первого, если их начала совмещены параллельным переносом.
Произведением вектора на число называется вектор, коллинеарный данному, длина которого равна произведению длины данного вектора на число. Если число 0 имеем пре(a*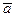 
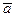
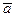
)=|a |*cosω=a*| |*cosω= aпре
при a 0 равен нулю).
или
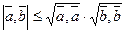
Скалярное произвкдкние векторов в коорднинатной форме
Пусть заданы два вектора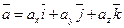 
и 
найдём скалярное произведение, используя таблицу скалярного произведени векторов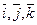 
: 
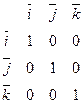
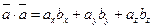
получится 
.
Скалярное произведение векторов равно сумме произведений их одноимённыйх координат
Векторное произведение двух векторов. Условие коллинеарносити двух векторов. Антикоммутативность векторного произведения. Векторное произведение в координатной форме.
Векторным призведением вектора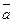 
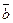
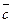
на вектор 
называестя вектор 
, который:
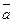
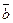
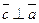
1) перпендикулярен векторам и , т.е 
и 
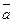
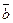
2) имеет длину, численно равную площади параллелонрамма, построенного на векторах и как на сторонах, т.е. 
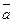
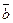
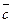
3) векторы , и образуют правую тройку.
Два вектора коллинеарны, если их векторное произведение равно нулю.
Вектороное произведение в координатной форме
, если заданы два вектора и
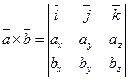
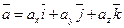
Смешанное произведение векторов. Условие компланарности трёх векторов. Смешанное произведение в координатной форме.
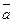
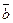
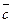
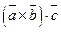
Смешанным произведением векторов , и называют векторно-скалярное произведение 
. Смешанное произведение есть число, равное объёму параллелипипеда, построенного этих векторах, взятому с +, если эти вектора образуют правую тройку, и с -, если левую.
Св-ва смешанного произведения:
1) не меняется при циклической перестановке сомножителей, т.е. 
2) не меняется при перемене мест знаков векторного и скалярного умножения
3) меняет знак при перемене мест любых двух векторов-сомножителей, т.е.
, 
, 
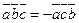
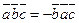
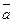
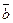
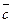
4) смешанное произведение ненулевых векторов , и равно нулю тогда и только тогда, когда они компланарны.
Выражение смешанного произведения черкз коорлинаты:
Смешанное произведение равно определителю третьего порядка, составленному из координат перемножаемых векторов.
Уравнение плоскости, проходящей через заданную точку и имеющую заданный нормальный вектор. Общее уравнение плоскости.
Пусть плоскость Q задана в пространстве точкой M0(x0,y0,z0) и вектором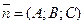 
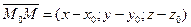
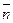
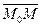
, перпендикулярным этой плоскости. Возьмём на плоскости точку M(x,y,z) и составим вектор 
При любом расположении точки M на плоскоти Q векторы 
и 
перендикулярны, поэтому их скалярное произведение рано нулю, т.е 
Общее уравнение плоскости: 
Геометрическое значение коэффициентов A, B, и С в общкм уравнении плоскости Ах+By+Cz+D=0
Состоит в том что они являются проекциями на координатные оси Ox,Oy, Oz вектораб перпендикулярного этой плоскости.
Положение прямой на плоскости может быть задано одним из следующих способов:
· прямая l проходит через точку 
параллельно вектору 
· прямая l проходит через точки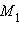 
и 
· прямая l проходит через точку перпендикулярно вектору 
· прямая l проходит через точку и составляет с вектором 
угол α (см. рис. 11.5.1).
 |
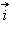
| Рисунок 11.5.1. |
Любой вектор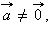 
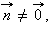
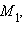
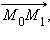
параллельный прямой l, называется направляющим вектором этой прямой. Любой вектор 
перпендикулярный прямой l, называется нормальным вектором прямой. Если взять на прямой какие-либо две фиксированные точки и 
то вектор 
в частности, будет направляющим вектором прямой 
Пусть прямая l задана точкой и направляющим вектором 
(см. рис. 11.5.2). Пусть M – произвольная точка прямой.
|
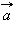
Обозначим
Переменная t, принимающая различные значения, называется параметром, а уравнение – векторно-параметрическим уравнением прямой. Если ввести систему координат
где
Эти уравнения называются параметрическими уравнениями прямой. Пусть Если
Это уравнение задает прямую, параллельную оси Oy и проходящую через точку
проходит через точку Как было отмечено ранее, направляющим вектором прямой можно выбрать вектор
Рассмотрим уравнение прямой, проходящей через две точки
Это уравнение называется уравнением прямой в отрезках, так как числа a и b указывают, какие отрезки отсекает прямая на осях координат. Пусть
Это уравнение прямой, проходящей через данную точку
В § 11.4 было показано, что любая прямая может быть задана этим уравнением при условии При рассмотрении векторно-параметрического уравнения прямой мы показали, как перейти к каноническому уравнению, из которого легко получить общее уравнение прямой. Аналогично, из нормального векторного уравнения так же легко перейти к общему уравнению прямой. Покажем теперь, как из общего уравнения прямой получить ее векторные уравнения. Пусть прямая задана общим уравнением Ax + By + C = 0 в прямоугольной декартовой системе координат. Тогда мы знаем, что вектор
Понятие о линейном пространстве. Единственность нулевого и противоположного элементов. Определение. Арифметическим вектором называятся упорядоченная совокупность n чисел. Обозначается Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число: Определение. Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством рифметических векторовR n . Вектор противоположным вектором для вектора Для любых 1. 2. 3. 4. 5. 6. 7. 8. Примерами пространства арифметических векторов являются пространства геометрических векторов на плоскости, записанных в координатной форме Линейные подпространства в R n , размерность подпространства, базис в подпространстве Определение. Множество L векторов из R n , такое, что для любых Пример.Множество L арифметических векторов из R n , у которых последние компоненты — нулевые, образует линейное подпространство в R n :
Определение. Число k называется размерностью линейного подпространства L, еслив L существует система из k линейно независимых векторов, а любые k+1 вектора — линейно зависимы; обозначаем dimL=k. Определение. Любая линейно независимая система из k векторов k-мерного линейного подпространства L образует базис линейного подпространства L. Это означает, что если dimL=k и арифметические векторы Примеры линейных пространств. 1). Пространства
С этими пространствами вы достаточно хорошо знакомы по курсам алгебры и анализа. 2). Непрерывные (действительные или комплексные) функции на некотором отрезке [a, b] с обычными операциями сложения функций и умножения их на числа образуют линейное пространство C[a, b], являющееся одним из важнейших в анализе и уже встречавшееся вам, например, при изучении функциональных рядов. 3). Пространство быстроубывающих функций 4). Пространство l2, в котором элементами служат последовательности чисел (действительных или комплексных)
является линейным пространством. Тот факт, что сумма двух последовательностей, удовлетворяющих условию (1), также удовлетворяет этому условию, вытекает из элементарного неравенства
Конечный набор элементов
В противном случае эти элементы называются линейно независимыми. Иными словами, элементы
вытекает, что Бесконечная система элементов пространства L называется линейно независимой, если любая ее конечная подсистема линейно независима. Если в пространстве L можно найти n линейно независимых элементов, а любые n+1 элементов этого пространства линейно зависимы, то говорят, что L имеет размерность n. Если же в L можно указать систему из произвольного конечного числи линейно независимых элементов, то говорят, что пространство L бесконечномерно. Легко понять, что в приведенных выше примерах 2)-4) пространства бесконечномерны, а в примере 1) — имеют размерность n. Непустое подмножество L‘ линейного пространства L называется подпространством, если оно само образует линейное пространство по отношению к опрелеленным в L операциям сложения и умножения на число. Иначе говоря, Если каждой паре векторов x, y линейного пространства L поставлено в соответствие действительное число (x, y), так, что для любых x, y и z из L и любого действительного числа α справедливы следующие аксиомы: (x, y) = (y, x), (α·x, y) = α·(x, y), (x + y, z) =(x, z) + (y, z), (x, x)> 0 при x ≠ 0, (0, 0) = 0, то в пространстве L определено скалярное произведение (x, y). Если в линейном пространстве определено скалярное произведение, то такое пространство называется евклидовым пространством. Евклидовы пространства E и E’ называются евклидово изоморфными, если они изоморфны как линейные пространства и если Фундаментальная система решенийСодержание: Одним из важнейших понятий в теории однородных систем линейных ОДУ является понятие фундаментальной системы решений. Определение 5.2. Линейно независимую в промежутке Теорема 5.7. Фундаментальные системы решений существуют. Пусть На основании теоремы 5.5 и определения 5.1 отсюда следует, что эти решения линейно независимы в промежутке Т и, согласно определению 5.2, образуют в нем фундаментальную систему решений для (5.3). По этой ссылке вы найдёте полный курс лекций по высшей математике: Запись в виде (5.3) соответствует нормальной однородной системе линейных ОДУ с переменными коэффициентами, поскольку элементы
Вычислим производную по t от определителя Вронского (5.6), составленного из решений В (5.8) использовано правило вычисления производной от определителя квадратной матрицы размера п [II]. Так как определитель представляет собой сумму
Возможно вам будут полезны данные страницы: Аналогично второе, третье и т.д. (вплоть до последнего) слагаемые в (5.8) равны: Пример с решением №1Рассмотрим нормальную систему ОДУ Решение: Матрица этой системы Итак, для двух произвольных решений ОДУ при ее численном интегрированииОПРЕДЕЛЕНИЕ. Система m линейных уравнений с п переменными называется однородной, если во всех ее уравнениях свободные члены равны нулю. В общем случае однородная система (или система однородных уравнений) имеет вид: Система линейных однородных уравнений всегда совместна, так как она всегда имеет, по крайней мере, нулевое (тривиальное) решение (0; 0; 0). Действительно, набор значений неизвестных ОПРЕДЕЛЕНИЕ. По отношению к системе (1.25) система (1.34) называется приведенной. Если в системе (1.34) ТЕОРЕМА 1.11. Система линейных однородных уравнений имеет ненулевое решение тогда и только тогда, когда ранг этой системы меньше числа ее неизвестных, т.е. при Следствие 1. Если число уравнений однородной системы меньше числа ее неизвестных, то эта система имеет ненулевое решение. Следствие 2. Если в однородной системе число уравнений равно числу неизвестных, то она имеет ненулевое решение тогда и только тогда, когда определитель матрицы системы равен нулю. Обозначим решение системы (1.34) Решения системы линейных однородных уравнений обладают следующими свойствами:1. Если строка 2. Если строки Убедиться в справедливости указанных свойств решений системы линейных однородных уравнений можно непосредственной подстановкой их в уравнения системы. Из сформулированных свойств следует, что всякая линейная комбинация решений системы линейных однородных уравнений также является решением этой системы. Поэтому целесообразно найти такие линейно независимые решения системы (1.34), через которые линейно выражались бы все остальные ее решения. ОПРЕДЕЛЕНИЕ. Система линейно независимых решений ТЕОРЕМА 1.12. Если ранг г матрицы однородной системы линейных уравнений (1.34) меньше числа неизвестных n, то всякая ее фундаментальная система решений состоит из Поэтому общее решение системы (1.34) линейных однородных уравнений имеет вид: где Для нахождения фундаментальной системы решений предположим, что ранг Пример с решением №2Найти решение и фундаментальную систему решения системы линейных однородных уравнений: Составим матрицу системы, и прямым ходом метода Гаусса приведем ее к ступенчатому виду: Из последнего уравнения находим
Поскольку ранг однородной системы равен четырем, то фундаментальная система решений для нее состоит из Положив значение свободной переменной Заметим, что если
Присылайте задания в любое время дня и ночи в ➔ Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института. Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды. Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги. источники: http://lektsia.com/3x76ac.html http://natalibrilenova.ru/fundamentalnaya-sistema-reshenij/ |
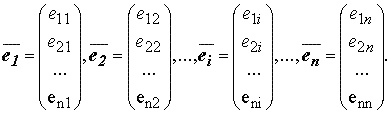
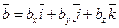
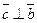
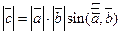
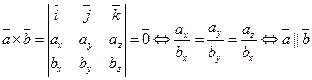
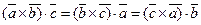
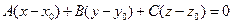
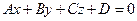
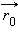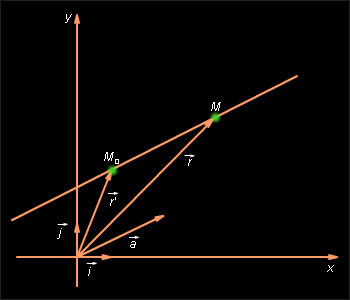
и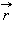 
радиус-векторы точек 
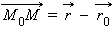параллелен прямой, и, следовательно, вектору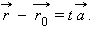 
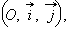то уравнение можно записать в виде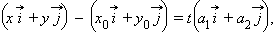
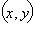и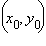 
– координаты точек 
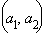– координаты вектора 
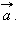Отсюда следует, что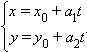
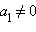и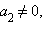 
тогда из уравнений следует, что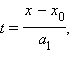 
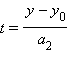и, окончательно, уравнение 
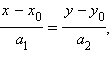которое называется каноническим уравнением прямой, с направляющим вектором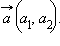 
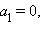то параметрическое уравнение примет вид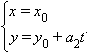
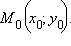Каноническое уравнение прямой имеет вид 
Аналогично, если 
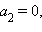то прямая, задаваемая системой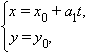
параллельно оси Ox. Ее каноническое уравнение имеет вид 
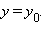
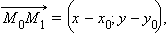где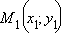 
– произвольные две точки прямой. Тогда, подставив координаты вектора 
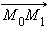в каноническое уравнение, получим уравнение прямой, проходящей через две заданные точки: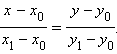
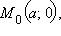а вторая лежит на оси Oy и имеет координаты 
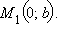Подставляя их в уравнение, получим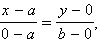
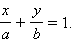
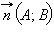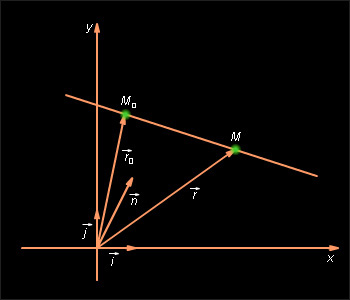
– вектор, перпендикулярный прямой, а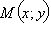 
– произвольная точка этой прямой (см. рис. 11.5.3). Тогда M лежит на прямой тогда и только тогда, когда вектор 
перпендикулярен вектору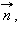 
а для этого необходимо и достаточно, чтобы скалярное произведение векторов 
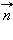и 
Введя радиус-векторы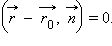 
Это – нормальное векторное уравнение прямой, а 
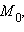M и вектор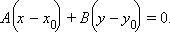 
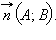Обозначив 
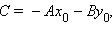окончательно имеем
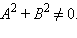Назовем это уравнение общим уравнением прямой. Следовательно, для любой прямой, заданной общим уравнением Ax + By + C = 0, можно считать, что вектор 
параллелен ей. Действительно, так как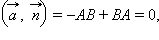 
векторы 
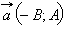– направляющий вектор прямой, 
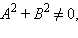предположим для определенности, что A ≠ 0. Тогда точка 
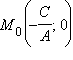принадлежит прямой. В этом легко убедиться, подставив координаты точки в уравнение прямой. Приведенных данных достаточно, чтобы получить векторные уравнения прямой. Действительно,
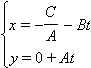– векторно-параметрическое уравнение;
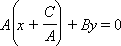– векторное нормальное уравнение.
, числа 
называются компонентами арифметического вектора.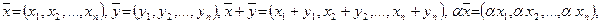
для любых 
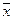и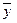 
и любого числа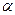 
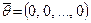называется нулевым вектором, а вектор 
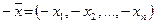— противопо
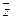из R n и любых чисел α , β справедливо:
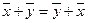, сложение коммутативно;
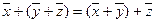,сложение ассоциативно;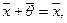
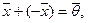
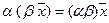, умножение на число ассоциативно;
;
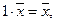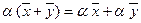, умножение на число дистрибутивно относительно сложения элементов;
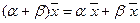, умножение вектора на число дистрибутивно относительно сложения чисел.
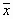и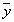 
из L и любого числа a справедливо 
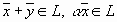, называется линейным подпространством в R n .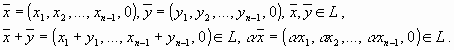
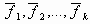из L линейно независимы, то для любого 
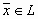существует единственный набор чисел 
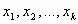таких, что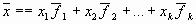 
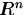и 
,состоящие из всевозможных (упорядоченных) наборов из n чисел (соответственно — действительных или комплексных). Сложение и умножение определяются формулами
,с которым вы работали, изучая преобразование Фурье.
линейного пространства L называется линейно зависимым, а сами элементы — линейно зависимыми, если существуют такие числа 
,не все равные нулю, что
.
есть подпространство, если из 
, 
следует, что 
при любых числах 
.
систему из 
вектор-функций вида (5.7), каждая из которых является в нем решением однородной системы п линейных ОДУ (5.3), называют фундаментальной системой решений для (5.3) в этом промежутке.
чисел
образуют единичную матрицу 
размера n, определитель которой 
Рассмотрим n решений 
однородной системы (5.3), которые определены в некотором промежутке 
числовой прямой 
точке 
удовлетворяют начальным условиям 
Тогда получим 
в промежутке Т.
матрицы A(t) этой системы являются функциями независимого переменного t.
системы ОДУ (5.3):
слагаемых с соответствующими знаками, а каждое слагаемое есть произведение п элементов, то, используя правило дифференцирования произведения п функций [II], приходим к записи (5.8). Вектор-функция 
является решением однородной системы (5.3), т.е. 
Поэтому первый определитель в правой части (5.8) имеет вид
С учетом этих выражений (5.8) принимает вид 
Отсюда следует, что определитель Вронского удовлетворяет линейному однородному ОДУ первого порядка с разделяющимися переменными. Разделяя переменные и интегрируя, получаем соотношение 
которое называют формулой Остроградского — Лиувил-ля (Ж. Лиувилль (1809-1882) — французский математик и механик, а о русском математике и механике М.В. Остроградском (1801-1861) см. Краткий исторический очерк.
где 
— произвольная функция, непрерывная в некотором промежутке 
.
Отсюда следует, что 
и формула Остроградского — Лиувилля принимает вид 
где 
рассматриваемой системы справедливо (5.11). Отметим, что (5.11) можно использовать для контроля точности получаемых решений системы
удовлетворяет всем уравнениям системы.
то она имеет только одно нулевое решение (см. теорему 1.7).
в виде строки 
— решение системы (1.34), то и строка 
— также решение этой системы.
— решения системы (1.34), то при любых с> и с2 их линейная комбинация 
— также решение данной системы.
называется фундаментальной, если каждое решение системы (1.34) является линейной комбинацией решений 
решений (или матрица фундаментальной системы имеет 
столбцов).
(1.35)
—любая фундаментальная система решений; 
— произвольные числа и 
Замечание. Общее решение системы 
линейных уравнений с п неизвестными (1.25) равно сумме общего решения соответствующей ей приведенной системы линейных уравнений (1.34) и произвольного частного решения этой системы (1.25).
Тогда базисные неизвестные этой системы 
линейно выражаются через свободные переменные 
Положим значения свободных переменных 
Затем находим второе решение, принимая 
Иными словами, мы последовательно присваиваем каждой свободной переменной единичное значение, положив остальные нулями.
Решение:
Выпишем систему уравнений: 
Обратный ход метода Гаусса дает значения базисных неизвестных 
выраженные через свободную переменную 
. Обозначим ее 
Затем, поднимаясь вверх по системе, определяем все неизвестные 
решения.
(других свободных переменных у нас нет), получим фундаментальное решение системы:
и решением будет нулевой вектор о; его называют тривиальным решением; этот вектор всегда есть среди решений однородной системы.
