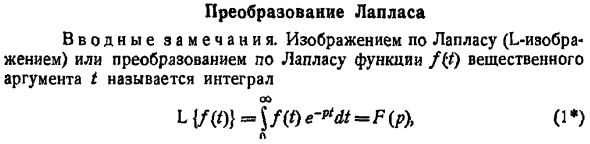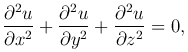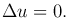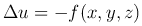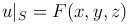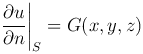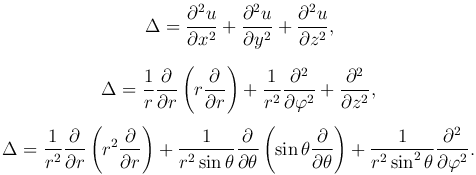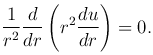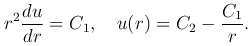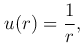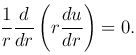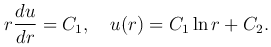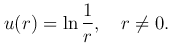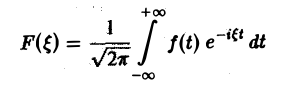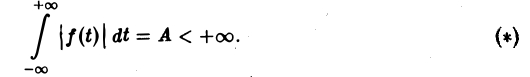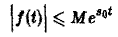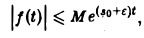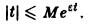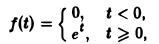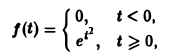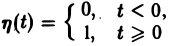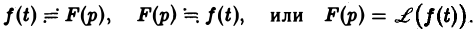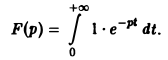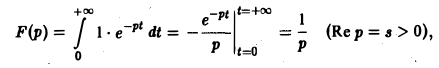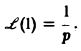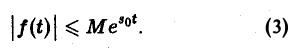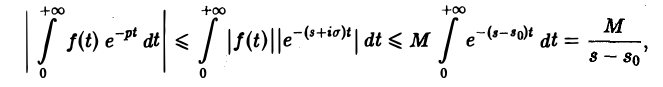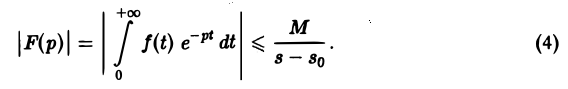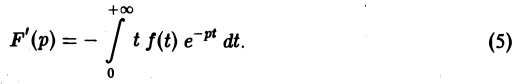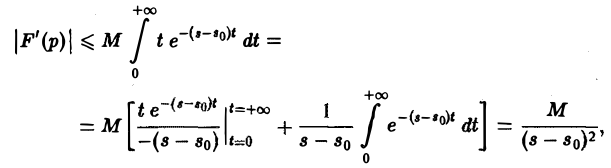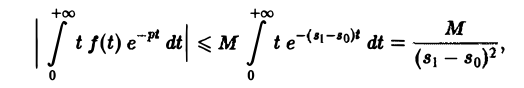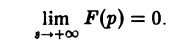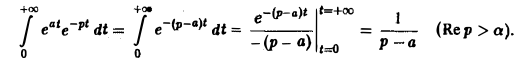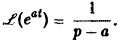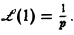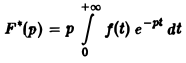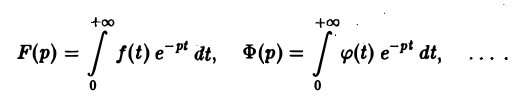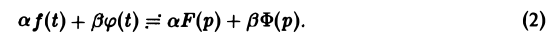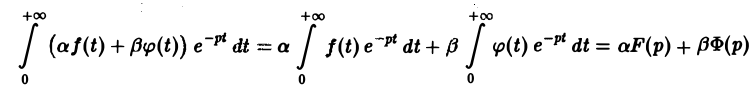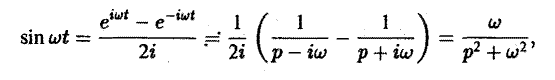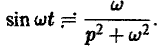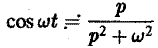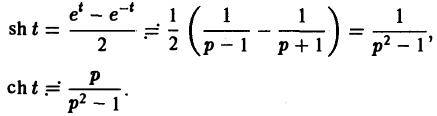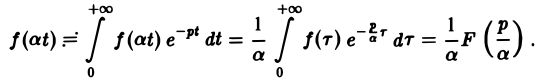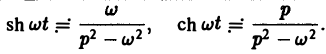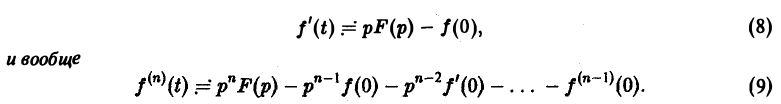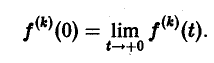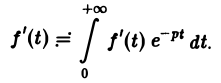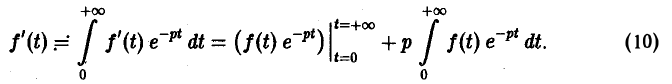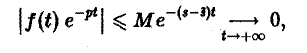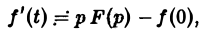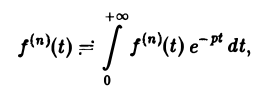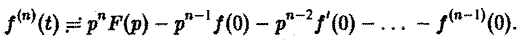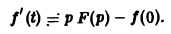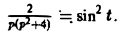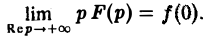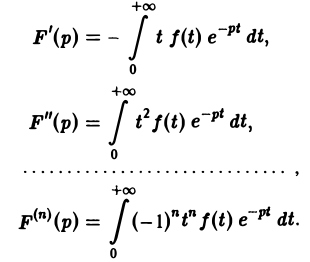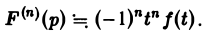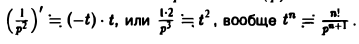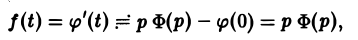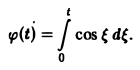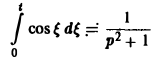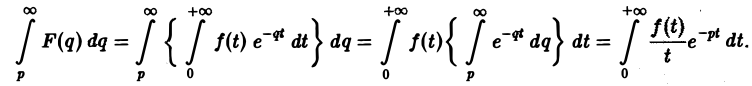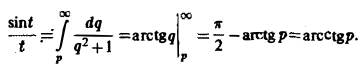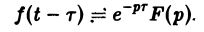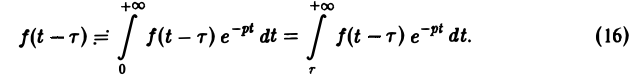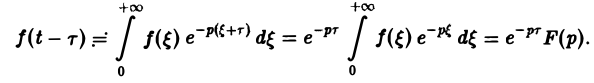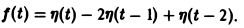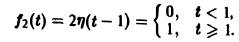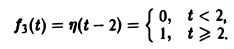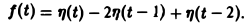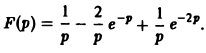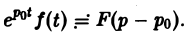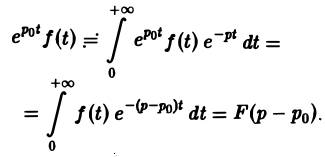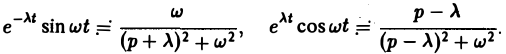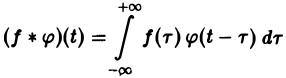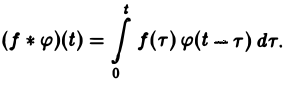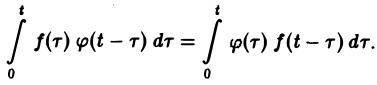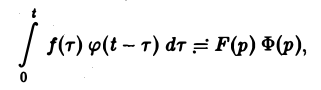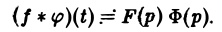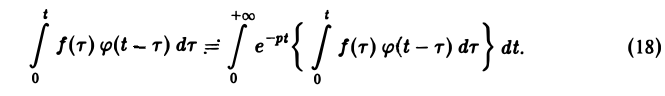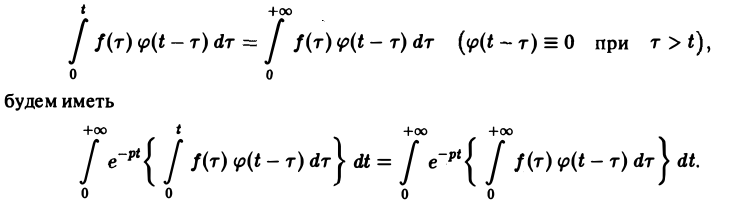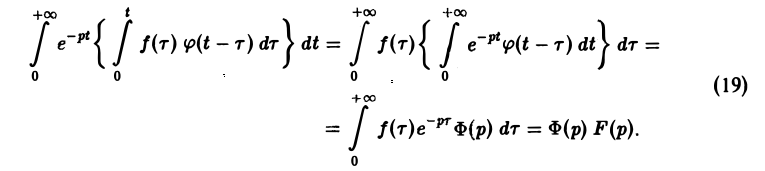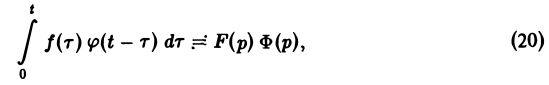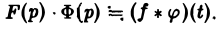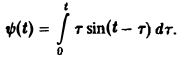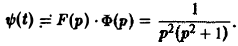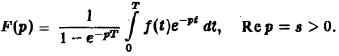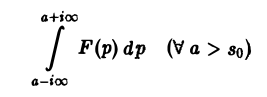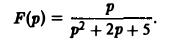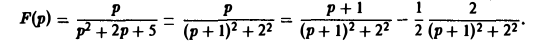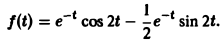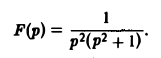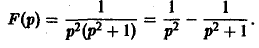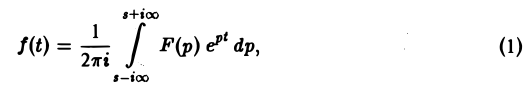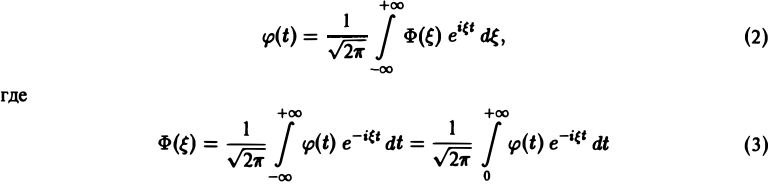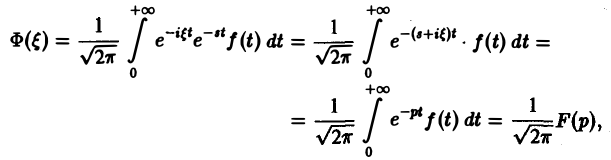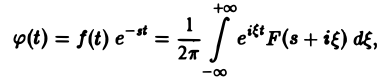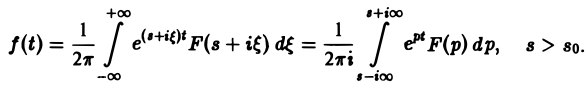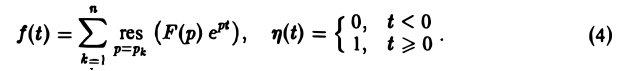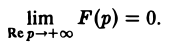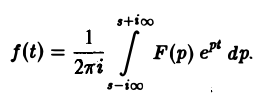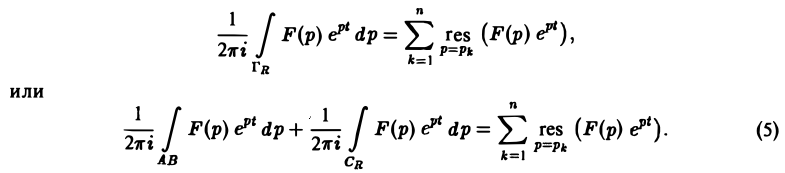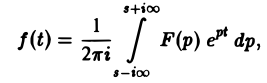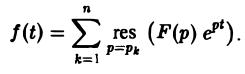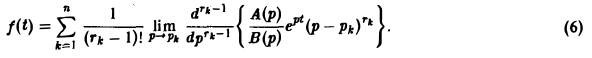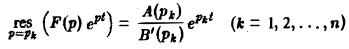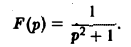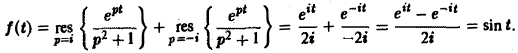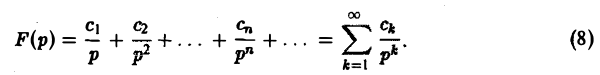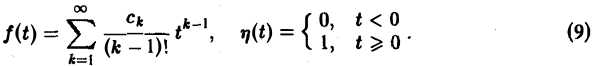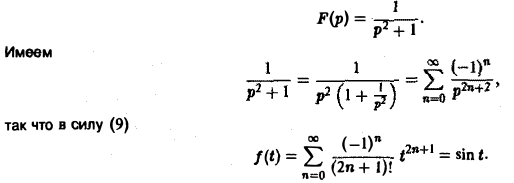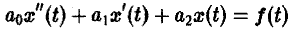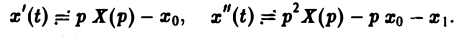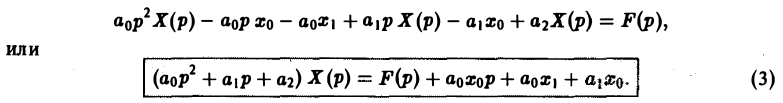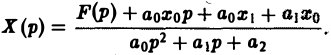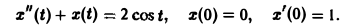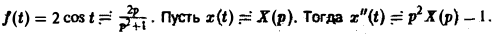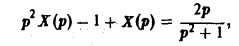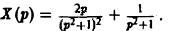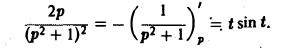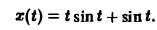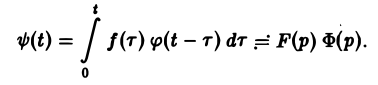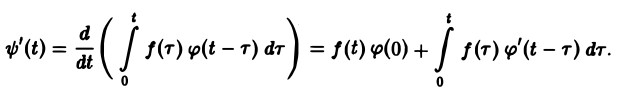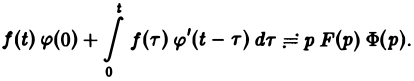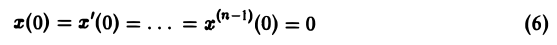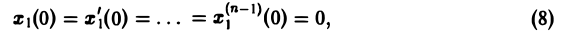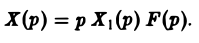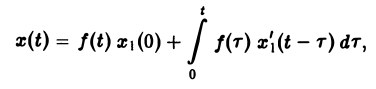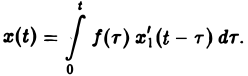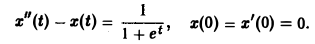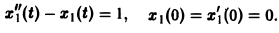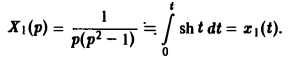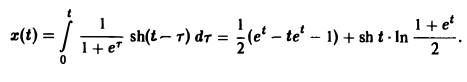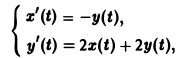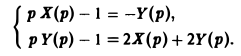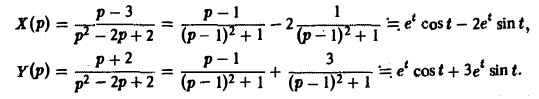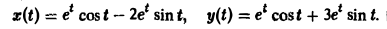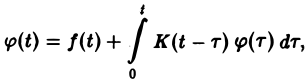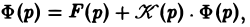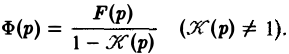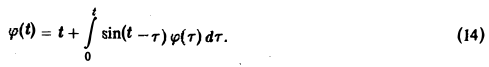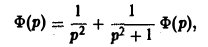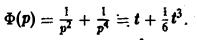Уравнение Лапласа
Рассмотрим уравнение с частными производными вида
где u=u(x, y, z). Это уравнение называется уравнением Лапласа.
Левая часть обозначается Δu и называется оператором Лапласа. Таким образом, это уравнение преобразуется к виду:
Данному уравнению удовлетворяет потенциал скорости безвихревого течения несжимаемой (с постоянной плотностью) жидкости; потенциал сил тяготения или сил взаимодействия электрических зарядов во всех точках пространства, находящихся вне притягивающих масс или вне зарядов, создающих поле; температура в однородном теле, если теплообмен является стационарным, т.е. температура u зависит только от места, но не от времени и др.
называется уравнением Пуассона.
Уравнение Лапласа и уравнение Пуассона является уравнениями эллиптического типа.
Определение. Функцию, непрерывную в некоторой области вместе со своими частными производными до второго порядка включительно и удовлетворяющую уравнению Лапласа, называют гармонической.
Обычно в задачах, связанных с уравнением Лапласа или Пуассона, искомое решение должно удовлетворять уравнению в области D, а также некоторому дополнительному условию на границе S области D.
Если надо определить функцию, гармоническую в области D, когда на границе S области D заданы ее значения, т.е.
(первая краевая задача), то такая задача называется задачей Дирихле.
Если же надо определить функцию, гармоническую в области D, когда на границе S задается значение нормальной производной
(вторая краевая задача), то такая задача называется задачей Неймана.
Определение. Если решение задачи ищут в области D, внутренней (внешней) по отношению к поверхности S, то соответствующую задачу называют внутренней (внешней) краевой задачей.
Фундаментальные решения уравнения Лапласа
Рассмотрим уравнение Лапласа
где оператор Лапласа в декартовой, цилиндрической и сферической системах координат определяется соответственно
Важную роль при решении задач для уравненийй Лапласа и Пуассона представляют решения, обладающие сферической или цилиндрической симметрией.
Найдем решение уравнения Лапласа, удовлетворяющее условию сферической симметрии, когда функция u зависит только от расстояния 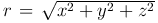
Интегрируя это уравнение, получим
которая удовлетворяет уравнению Лапласа всюду, кроме точки r=0, где она обращается в бесконечность. Такую функцию называют фундаментальным решением уравнения Лапласа в пространстве.
В задаче с осевой симметрией, когда функция u в цилиндрической системы координат не зависит от φ и z, уравнение Лапласа имеет вид
Интегрируя это уравнение, получим
Эта функция называется фундаментальным решением уравнения Лапласа на плоскости.
ТЕМА: Уравнения эллиптического типа
ТИТУЛЬНЫЙ ЛИСТ
1 Теоретические обоснования уравнений эллиптического типа………………. 4
1.1. Задачи приводящие к уравнению Лапласа………………. 5
1.2. Уравнение Шредингера и его стационарный аналог. 9
1.3. Уравнение Гельмгольца……………………………………………. ……10
2 Примеры решения задач на уравнения эллиптического типа……………………12
Список использованных источников……………………………………………. …16
В курсовой работе будут рассмотрены уравнения эллиптического типа.
Актуальность исследования заключается в том, что благодаря данному типу уравнений можно описать стационарные процессы, проходящие в различных физических полях. Например, с помощью уравнения Пуассона можно описать электростатическое поле, поле давления [1].
Исследование затронет следующие проблемы: применение уравнений эллиптического типа на практике и способы их решения.
Целью исследования является: изучение вопроса, касающегося применения уравнений эллиптического типа на практике.
Основными задачами, поставленными для достижения цели можно считать:
— ознакомиться с положениями, характеризующими уравнения эллиптического типа;
— выявить основные уравнения, относящиеся к данному типу;
— освоить навык решения задач, используя данные уравнения;
— показать специфику проблем, которые могут возникнуть на этапах решения.
Объектом исследования заданной темы являются дифференциальные уравнения в частных производных.
Предметом исследования выступают уравнения эллиптического типа.
Теоретической и методологической основой исследования послужили труды отечественных и зарубежных деятелей, методические пособия по дисциплине «методы математической физики».
1. ТЕОРЕТИЧЕСКИЕ ОБОСНОВАНИЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
Помимо физических явлений, развивающихся в пространстве и во времени, существует множество процессов, которые не изменяются с течением времени. Эти процессы называются стационарными. При исследовании данных процессов, различной физической природы (колебания, теплопроводность, диффузия и др.) обычно приходят к уравнениям эллиптического типа. Примерами могут выступать:
1. Уравнения Лапласа и Пуассона, описывают различные стационарные физические поля.
2. Стационарный аналог уравнения Шредингера, когда предполагается гармоническая зависимость от времени.
3. Уравнение Гельмгольца.
4. Уравнения, получаемые из уравнения Максвелла, если предполагается, что электромагнитное поле не изменяется с течением времени [1].
Наиболее распространенным уравнением этого типа является уравнение Лапласа

Этим уравнением характеризуется гравитационный и электростатический потенциалы в точках свободного пространства, оно описывает потенциал скорости безвихревого потока несжимаемой жидкости, и оно же справедливо для температуры однородной изотропной среды при установившемся движении тепла.
Функция 

При изучении свойств гармонических функций были разработанные различные математические методы, оказавшиеся плодотворными и в применении к уравнениями гиперболического и параболического типов [1].
1.1. ЗАДАЧИ ПРИВОДЯЩИЕ К УРАВНЕНИЮ ЛАПЛАСА
1. Стационарное тепловое поле. Постановка краевых задач.
Рассматривается стационарное тепловое поле. Температура нестационарного теплового может быть представлена дифференциальным уравнением теплопроводности
Если процесс стационарен, то устанавливается распределение температуры 
 | (1) |
При наличии источников тепла получается уравнение
 | (2) |
где 

Рассматривается некоторый объем 



Найти функцию 
 , , | (3) |
и граничному условию, которое может быть взято в одном из следующих видов:
I. 

II. 

III. 

где 




Первую краевую задачу называют для уравнений Лапласа часто называют задачей Дирехле, а вторую задачу – задачей Неймана.
Если ищется решение в области 

2. Потенциальное течение жидкости. Потенциал стационарного тока и электростатического поля.
В качестве второго примера будет рассмотрено потенциальное течение жидкости без источников. Пусть внутри некоторого объема 




 | (4) |
где 
 . . | (5) |
При подстановке сюда выражения (3) для υ, выходит:

 , , | (6) |
то есть потенциал скорости удовлетворяет уравнению Лапласа.
Пусть в однородной проводящей среде имеется стационарный ток с объемной плотностью 
 . . | (7) |
Электрическое поле 
 | (8) |
где 
Поскольку процесс стационарный, то электрическое поле является безвихревым или потенциальным, т.е. существует такая скалярная функция 
  ). ). | (9) |
Отсюда на основании формул (6) и (7) заключается, что
 , , | (10) |
т.е. потенциал электрического поля стационарного тока удовлетворяет уравнению Лапласа.
Рассматривается электрическое поле стационарных зарядов. Из стационарности процесса следует, что
 , , | (11) |
т.е. поле является потенциальным и
 . . |
Пусть 

Исходя из основного закона электродинамики
 | (12) |
где 



 | (13) |

При подстановке сюда выражение (8) для 
 , , | (14) |
т.е. электростатический потенциал 


Нами был рассмотрен ряд процессов. Основные краевые задачи для которых относятся к трем типам, приведенным выше [1].
1.2. УРАВНЕНИЕ ШРЕДИНГЕРА И ЕГО СТАЦИОНАРНЫЙ АНАЛОГ
В квантовой механике состояние частицы описывается волновой функцией 


где 


Уравнение Шредингера является уравнением в частных производных второго порядка по координатам, но первого порядка по времени. В отличие от волнового уравнения, чтобы выделить частное решение из общего, надо задавать при 
Если искать решение в виде стационарных состояний 

 | (15) |
Требуется найти не только решение 

1.3 УРАВНЕНИЕ ГЕЛЬМГОЛЬЦА
Эллиптическое дифференциальное уравнение в частных производных, получаемое из уравнение Максвелла, если предполагается, что электромагнитное поле либо не меняется с течением времени, либо меняется по гармоническому закону. Может быть представлено как
где 



В уравнение Гельмгольца не входят операторы дифференцирования по времени, следовательно, сведение исходной задачи в частных производных к уравнению Гельмгольца может упростить её решение. Для примера рассматривается волновое уравнение:
 | (16) |
Пусть функции 




 | (17) |
где 

Решение уравнения Гельмгольца зависит от вида граничных условий. В двумерном случае уравнение Гельмгольца применяется для решения задачи о колеблющейся мембране, тогда естественным образом задаются однородные граничные условия, что физически соответствует закреплению мембраны на границе. В таком случае решение будет зависеть от формы мембраны. Так, для круглой мембраны радиуса 

 | (18) |
Метод разделения переменных позволяет перейти к задаче на собственные значения для части решения, зависящей только от 
 | (19) |
 | (20) |
а функция, зависящая только от радиуса, будет удовлетворять уравнению:
 | (21) |
Фундаментальными решениями этих уравнений являются, соответственно, функции 

2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
В отличие от смешанных задач, для эллиптических уравнений ставится только краевая задача
где 

При этом, если 


Задачи буду решаться в полярных или сферических координатах. Заданные краевые условия произвольные, неоднородные. Однородные краевые условия для нахождения собственных функций возникают из-за того, что области имеют специальный вид, а потому решение должно иметь период 


Предлагаю рассмотреть метод нахождения решения уравнения Лапласа 


где 
Задача № 1. Решить краевую задачу для уравнения 


Решение: Уравнение Лапласа в полярных координатах 
 | (22) |
1. Частное решение уравнения в соответствии с методом Фурье ищется в виде
причем 

При подстановке 
Поэтому функции 

a)
b)
2. Решается задача
Общее решение уравнения 
 | (23) |
где 

Это решение периодично при 

Если
Если
3. Решается задача
Если 

Если 
Общее решение этого уравнения
Так как
4. Вспомогательные решения имеют вид:
5. Тогда решение исходной задачи ищется в виде
6. При использовании граничного условия 
получается 

Ответ:
Задача № 2. Решить краевую задачу
Решение: Проводятся преобразования, аналогичные предыдущей задачи до момента нахождения коэффициентов 
Нужно представить граничное условие в виде
Следовательно,
Далее предлагаю рассмотреть примеры решения краевых задач уравнения Гельмгольца.
Задача № 3. Решить краевую задачу для уравнения Гельмгольца в круге
(здесь 


Решение: Используя метод разделения переменных (метод Фурье). Полагая, 
где 
Собственные значения и собственные функции определяются как решения данной задачи:
Выходит
то для определения 
 | (24) |
Обозначив 
Это уравнение Бесселя порядка 
где 



Значит, решение уравнения (1) имеет вид
Поскольку 


 | (25) |
Постоянные 

В частности, при 
и в этом случае решение имеет вид
В проделанной нами работе, мы акцентировали внимание на такой теме как «Уравнения эллиптического типа». В ходе нашего исследования мы сумели выполнить поставленные перед нами задачи, что повлекло за собой достижение цели работы. Изучив теоретические материалы, мы разобрались с основными уравнениями, научились выводить их и применять в решениях задач. Были обозначены проблемы и пути их решения. В качестве примера выступили три задачи, требующие решение эллиптического уравнения.
Материалом данного исследования выступали труды советских и российских деятелей, содержащие в себе подробную информацию, касающуюся нашей проблемы.
В ходе выполнения данной работы появилась возможность оценить важность заданной темы в современной науке, определить основные задачи, которые можно решать с помощью уравнений эллиптического типа.
Подводя итог, хочется отметить, что изучение данного вопроса способствовала возникновению большого интереса, что позволило с энтузиазмом продолжать с ознакомлением трудов знаменитых авторов для дальнейшего анализа и использования в работе.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1.А.Н. Тихонов, А.А. Самарский, Уравнения математической физики М., издательство «наука», 1977. – 735 с.
2. Л.Д. Ландау, Е. М. Лифшиц, Квантовая механика,
М., Изд. 4е, «Наука», 1989. – 767 с.
3. Д.А. Шапиро, Конспект лекций по методам математической физики ч.1, кафедра теоретической физики НГУ, 2004. – 123 с.
4. В. С. Владимиров, В. В. Жаринов, Уравнения математической физики. — М.: «Физматлит», 2004. – 400 с.
5. С.И. Колесникова, Методы решения основных задач уравнений математической физики, М., МФТИ, 2015. – 80 с.
Преобразование Лапласа с примерами решения и образцами выполнения
Ранее мы рассмотрели интегральное преобразование Фурье
с ядром K(t, ξ) = 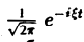
Преобразование Фурье неудобно тем, что должно быть выполнено условие абсолютной интегрируемости функции f(t) на всей оси t,
Преобразование Лапласа позволяет освободиться от этого ограничения.
Определение:
Функцией-оригиналом будем называть всякую комплекснозначную функцию f(t) действительного аргумента t, удовлетворяющую следующим условиям:
- f(t) непрерывна на всей оси t, кроме отдельных точек, в которых f(t) имеет разрыв 1-го рода, причем на каждом конечном интервале оси t таких точек может быть лишь конечное число;
- функция f(t) равна нулю при отрицательных значениях t, f(t) = 0 при t 0 и з такие, что для всех t
Ясно, что если неравенство (1) выполняется при некотором s = s1, то оно будет выполнятся при всяком s2 > s1.
Точная нижняя грань sо всех чисел s, so = infs, для которых выполняется неравенство (1), называется показателем роста функции f(t).
Замечание:
В общем случае неравенство
не имеет места, но справедлива оценка
где ε > 0 — любое. Так, функция f(t) = t, t ≥ 0, имеет показатель роста so =0. Для нее неравенство |t| ≤ М ∀t ≥ 0 не выполняется, но ∀ε > О, ∀t > 0 верно неравенство
Условие (1) гораздо менее ограничительное, чем условие (*).
Пример:
не удовлетворяет условию (*), но условие (1) выполнено при любом s ≥ 1 и М ≥ 1; показатель роста so = 1. Так что f(t) является функцией-оригиналом. С другой стороны, функция
не является функцией-оригиналом: она имеет бесконечный порядок роста, sо = +∞. Простейшей функцией-оригиналом является
так называемая единичная функция
Если некоторая функция φ(t) удовлетворяет условиям 1 и 3 определения 1, но не удовлетворяет условию 2, то произведение f(t) = φ(t) η(t) уже является функцией-оригиналом.
Для простоты записи мы будем, как правило, множитель η(t) опускать, условившись, что все функции, которые мы будем рассматривать, равны нулю для отрицательных t, так что если речь идет о какой-то функции f(t) например, о sin t, cos t, e t и т. д., то всегда подразумеваются следующие функции (рис. 2):
Определение:
Пусть f(t) есть функция-оригинал. Изображением функции f(t) по Лапласу называется функция F(p) комплексного переменного р = s + iσ, определяемая формулой
где интеграл берется по положительной полуоси t. Функцию F(p) называют также преобразованием Лапласа функции f(t); ядро преобразования K(t, р) = e -pt .
Тот факт, что функция f(x) имеет своим изображением F(p), будем записывать так:
Пример:
Найти изображение единичной функции η(t).
Функция 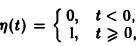
Если р = s + iσ, то при s > 0 интеграл в правой части последнего равенства будет сходящимся, и мы получим
так что изображением функции η(t) будет функция 1/p. Как мы условились, будем писать, что η(t) = 1, и тогда полученный результат запишется так:
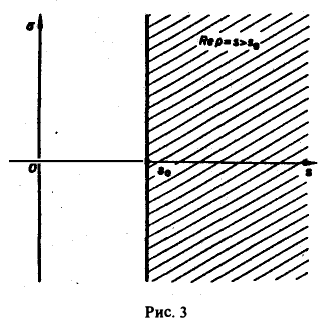
Теорема:
Для всякой функции-оригинала f(t) с показателем роста sо изображение F(p) определено в полуплоскости Re p = s > So и является в этой полуплоскости аналитической функцией (рис. 3).
Для доказательства существования изображения F(p) в указанной полуплоскости достаточно установить, что несобственный интеграл (2) абсолютно сходится при s > so. Используя (3), получаем
что и доказывает абсолютную сходимость интеграла (2). Одновременно мы получили оценку преобразования Лапласа F(p) в полуплоскости сходимости Re р = s > so
Дифференцируя выражение (2) формально под знаком интеграла по р, находим
Существование интеграла (5) устанавливается так же, как было установлено существование интеграла (2).
Применяя для F'(p) интегрирование по частям, получаем оценку
откуда следует абсолютная сходимость интеграла (5). (Внеинтегральное слагаемое 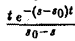
не зависящим от р. Следовательно, дифференцированиепо р законно и равенство (5) справедливо.
Поскольку производная F'(p) существует, преобразование Лапласа F(p) всюду в полуплоскости Re p = s > sо является аналитической функцией.
Из неравенства (4) вытекает
Следствие:
Если точка р стремится к бесконечности так, что Re р = s неограниченно возрастает, то
Пример:
Найдем еще изображение функции f(t) =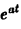
Показатель роста sо функции f(t) равен а.
Считая Rep = s> а, получим
При а = 0 вновь получаем формулу
Обратим внимание на то, что изображение функции 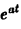
Замечание:
В операционном исчислении иногда пользуются изображением функции f(t) по Хевисайду, определяемым равенством
и отличаюикмся от шоСражения по Лапласу множителем р.
Свойства преобразования Лапласа
В дальнейшем через f(t), φ(t), … будем обозначать функции-оригиналы, а через F(p), Ф(р), … — их изображения по Лапласу,
Из определения изображения следует, что если f(t) = 9 ∀t, то F(p) = 0.
Теорема единственности:
Теорема:
Справедливость утверждения вытекает из свойства линейности интеграла, определяющего изображение:
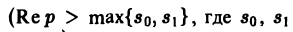
На основании этого свойства получаем
Аналогично находим, что
(4)
Теорема подобия:
Если f(t) — функция-оригинал и F(p) — ее изображение по Лапласу, то для любого постоянного а > 0
Полагая at = т, имеем
Пользуясь этой теоремой, из формул (5) и (6) получаем
Теорема:
О дифференцировании оригинала. Пусть f(t) является функцией-оригиналом с изображением F(p) и пусть 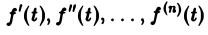
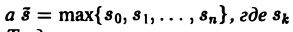
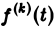
Здесь под fk(0) (k = 0,1,… , п — 1) понимается правое предельное значение 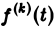
Пусть f(t) = F(p). Найдем изображение f'(t). Имеем
Интегрируя по частям, получаем
Внеинтегральное слагаемое в правой части (10) обращается в нуль при t → + ∞, т. к. при Re р = s > 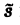
подстановка t = 0 дает -f(0).
Второе слагаемое справа в (10) равно pF(p). Таким образом, соотношение (10) принимаетвид
и формула (8) доказана. В частности, если f(0) = 0, то f'(t) = pF(p). Для отыскания изображения 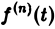
откуда, интегрируя п раз по частям, получим
Пример:
Пользуясь теоремой о дифференцировании оригинала, найти изображение функции f(t) = sin 2 t.
Пусть f(t) = F(p). Тогда
Но f(0) = О, а f'(0) = 2 sin t cos t = sin 2t = 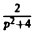
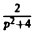
Теорема 5 устанавливает замечательное свойство интегрального преобразования Лапласа: оно (как и преобразование Фурье) переводит операцию дифференцирования в алгебраическую операцию умножения на р.
Формула включения. Если f(t) и f'(t) являются функциями-оригиналами, то (11)
В самом деле, f'(
Так как функция F(p) в полуплоскости Rep = s > so является аналитической, то ее можно дифференцировать по р. Имеем
Последнее как раз и означает, что
Пример:
Пользуясь теоремой 6, найти изображение функции 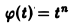
Как известно, 1 = 1/p. Здесь f(t) = 1, F(p) = 1/p. Отсюда (1/p)’= (-t) • 1, или 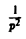
Теорема:
Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р: если f(t) = F(p), то
Нетрудно проверить, что если f(t) есть функция-оригинал, то и φ(t) будет функцией-оригиналом, причем φ(0) = 0. Пусть φ(t) = Ф(р). В силу (14)
С другой стороны, f(t) =’ F(p), откуда F(p) = рФ(р), т.е. Ф(р) =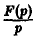
Последнее равносильно доказываемому соотношению (13).
Пример:
Найти изображение функции
В данном случае f(t) = cos t, так что F(p) = 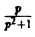
Теорема:
Интегрирование изображения. Если f(t) = F(p) и интеграл 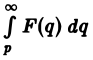
Предполагая, что путь интегрирования (р, ∞) лежит в полуплоскости Re p ≥ а> so, мы можем изменить порядок интегрирования (t > 0):
Последнее равенство означает, что 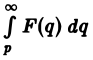
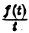
Пример:
Найти изображение функции 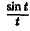
Как известно, sin t = 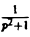
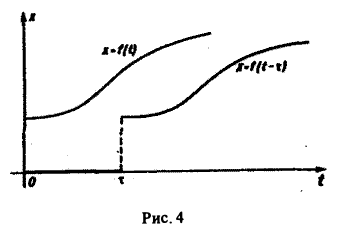
Теорема запаздывания:
Положим ξ = t- τ. Тогда dt = d ξ. При t = τ получаем ξ = 0, при t = + ∞ имеем ξ = + ∞.
Поэтому соотношение (16) принимает вид
Пример:
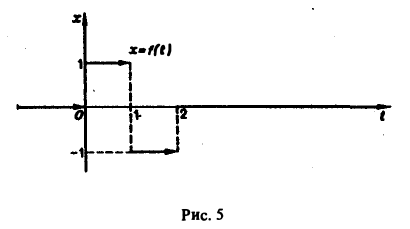
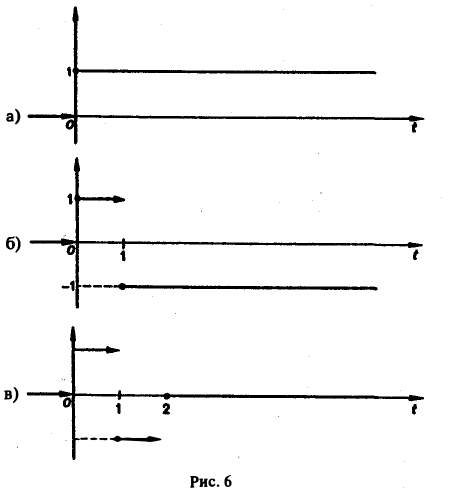
Найти изображение функции f(t), заданной графически (рис. 5).
Запишем выражение для функции f(t) в следующем виде:
Это выражение можно получить так. Рассмотрим функцию f1(t) = η(t) для t ≥ 0 (рис. 6 а) и вычтем из нее функцию
Разность f(t) — h(t) будет равна единице для t ∈ [0,1) и -1 для t ≥ 1 (рис. 6 b). К полученной разности прибавим функцию
В результате получим функцию f(t) (рис. 6 в), так что
Отсюда, пользуясь теоремой запаздывания, найдем
Теорема смещения:
Теорема позволяет по известным изображениям функций находить изображения тех же функций, умноженных на показательную функцию 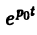
Свертка функций. Теорема умножения
Пусть функции f(t) и φ(t) определены и непрерывны для всех t. Сверткой (f *φ)(t) этих функций называется новая функция от t, определяемая равенством
(если этот интеграл существует).
Для функций-оригиналов f(t) и φ(t) операция свертки всегда выполнима, причем
(17)
В самом деле, произведение функций-оригиналов f( τ ) φ(t — τ), как функция от τ, является финитной функцией, т.е. обращается в нуль вне некоторого конечного промежутка (в данном случае вне отрезка 0 ≤ τ ≤ t). Для финитных непрерывных функций операция свертки выполнима, и мы получаем формулу (17).
Нетрудно проверить, что операциясвертки коммутативна,
Теорема умножения:
Нетрудно проверить, что свертка (f * φ)(t) функций-оригиналов есть функция-оригинал с показателем роста s* = mах
показатели роста функций f(t) и φ(t) соответственно. Найдем изображение свертки,
Воспользовавшись тем, что
Меняя порядок интегрирования в интеграле справа (при Re р = s > s* такая операция законна) и применяя теорему запаздывания, получим
Таким образом, из (18) и (19) находим
— умножению изображений отвечает свертывание оригиналов,
Пример:
Найти изображение функции
Функция ψ(t) есть свертка функций f(y) = t и φ(t) = sin t. В силу теоремы умножения
Задача:
Пусть функция f(t), периодическая с периодом Т, есть функция-оригинал. Показать, что ее изображение по Лапласу F[p) дается формулой
Отыскание оригинала по изображению
Задача ставится так: дана функция F(p), надо найти функцию f(t). изображением которой является F(p).
Сформулируем условия, достаточные для того, чтобы функция F(p) комплексного переменного р служила изображением.
Теорема:
Если аналитическая в полуплоскости Rep = s > so функция F(p)
1) стремится к нулю при |р| —» + ∞ в любой полуплоскости Re р = а > So равномерно относительно arg р;
сходится абсолютно, то F(p) является изображением некоторой функции-оригинала f
Задача:
Может ли функция F(p) = 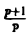
Отыскание оригинала с помощью таблиц изображений
Прежде всего стоит привести функцию F(p) к более простому, «табличному» виду. Например, в случае, когда F(p) — дробно-рациональная функция аргумента р,ее разлагают на элементарные дроби и пользуются подходящими свойствами преобразования Лапласа.
Пример:
Найти оригинал для
Запишем функцию F(p) в виде:
Пользуясь теоремой смещения и свойством линейности преобразования Лапласа, получаем
Пример:
Найти оригинал для функции
Запишем F(p) в виде
Отсюда f(t) = t — sin t.
Использование теоремы обращения и следствий из нее
Теорема обращения:
где интеграл берется вдоль любой прямой Re p = s > So и понимается в смысле главного значения, т. е. как
Формула (1) называется формулой обращения преобразования Лапласа, или формулой Меллина. В самом деле, пусть, например, f(t) — кусочно-гладкая на каждом конечном отрезке [0, а] функция-оригинал-с показателем роста so. Рассмотрим функцию φ(t) = 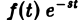
Функция φ(t) удовлетворяет условиям применимости интегральной формулы Фурье, и, следовательно, справедлива формула обращения преобразования Фурье,
(φ(t) ≡ 0 при t
откуда получаем формулу обращения преобразования Лапласа
Как следствие из теоремы обращения получаем теорему единственности.
Теорема:
Две непрерывные функции f(t) и φ(t), имеющие одно и то же изображение F(p), тождественны.
Непосредственное вычисление интеграла обращения (1) обычно затруднительно. Отыскание оригинала по изображению упрощается при некоторых дополнительных ограничениях на F(p).
Теорема:
Пусть изображение F(p) — дробно-рациональная функция с полюсами р1, p2….pп. Тогда оригиналом для F(p) будет функция f(t) η(t), где
Пусть изображение F(p) — дробно-рациональная функция, F(p) = 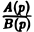
Пусть корни знаменателя В(р), являющиеся полюсами изображения F(p), суть р1, р2, …, рп, а их кратности равны r1, r2, …, rп соответственно.
Если число s, фигурирующее в формуле (1), взять большим всех Re pk (k = 1,2,…, п), то по формуле обращения, которая в этих условиях применима, получим
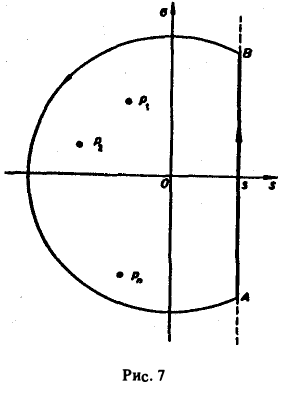
Рассмотрим замкнутый контур ГR (рис.7), состоящий из дуги CR окружности радиуса R с центром в начале координат и стягивающей ее хорды АВ (отрезка прямой Re р = s), и проходимый в положительном направлении, причем радиус R настолько велик, что все полюсы F(p) лежат внутри ГR.
По теореме Коши о вычетах при любом R, удовлетворяющем указанному условию, будем иметь
Второе слагаемое слева в равенстве (5) стремится к нулю при R → ∞. Это следует из леммы Жордана, если в ней заменить р на iz и учесть, что F(p) → 0 при Re p → + ∞. Переходя в равенстве (5) к пределу при R → ∞, мы получим слева
а справа — сумму вычетов по всем полюсам функции F(p)
Замечание:
Воспользовавшись формулой для вычисления вычетов, найдем, что
Если все полюсы p1, р2,…, рn — простые, то
и формула (6) принимает вид
Пример:
Найти оригинал для функции
Функция F(p) имеет простые полюсы р1 = i. p2 = -i. Пользуясь формулой (7), находим
Теорема:
Пусть изображение F(p) является аналитической функцией в бесконечно удаленной точке р = ∞, причем ее разложение в окрестности |р| > R бесконечно удаленной точки имеет вид
Тогда оригиналом для F(p) будет функция f(t) η
Пример:
Приложения преобразования Лапласа (операционного исчисления)
Решение линейных дифференциальных уравнений с постоянными коэффициентами
Дано линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
(1)
(ао, а1, а2 — действительные числа) и требуется найти решение уравнения (1) для t > 0, удовлетворяющее начальным условиям
Будем считать, что f(t) есть функция-оригинал. Тогда x(t) — также функция-оригинал. Пусть
f(t) = F(p), x(t) = X(p).
По теореме о дифференцировании оригинала имеем
Перейдем в уравнении (1) от оригиналов к изображениям. Имеем
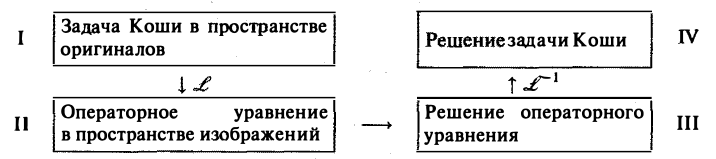
Это уже не дифференциальное, а алгебраическое уравнение относительно изображения Х(р) искомой функции. Его называют операторным уравнением. Решая его, найдем операторное решение задачи (1)-(2) —
Оригинал для Х(р) будет искомым решением х(t) задачи (1)-(2).
Общий случай линейного дифференциального уравнения n-го порядка (n ≥ 1) с постоянными коэффициентами от случая п = 2 принципиально ничем не отличается.
Приведем общую схему решения задачи Коши
Здесь 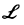
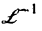
Пример:
Решить задачу Коши
По теореме о дифференцировании изображения
Формула Дюамеля
В приложениях операционного исчисления к решению дифференциальных уравнений часто пользуются следствием из теоремы умножения, известным под названием формулы Дюамеля.
Пусть f(t) и φt) — функции-оригиналы, причем функция f(t) непрерывна на [0, + ∞), a φ(t) — непрерывно дифференцируема на [0,+ ∞). Тогда если f(t) = F(p), φ Нетрудно проверить, что функция ψ(t) непрерывно дифференцируема на [0, + ∞), причем Отсюда, в силу правила дифференцирования оригиналов, учитывая, что ψ(0) = 0, получаем формулу Дюамеля Покажем применение этой формулы. Пусть требуется решить линейное дифференциальное уравнение n-го порядка (n ≥ 1) с постоянными коэффициентами при нулевых начальных условиях (последнее ограничение несущественно: задачу с ненулевыми начальными условиями можно свести к задаче с нулевыми условиями заменой искомой функции). Если известно решение x(t) дифференциального уравнения с той же левой частью и правой частью, равной единице, L[x(t)] = l (7) при нулевых начальных условиях то формула Дюамеля (4) позволяет сразу получить решение исходной задачи (5)-(6). В самом деле, операторные уравнения, отвечающие задачам (5)-(6) и (7)-(8), имеют соответственно вид где F(p) — изображение функции f(t). Из (9) и (10) легко находи Отсюда по формуле Дюамеля или, поскольку x1(0) = 0, (11) Пример: Решить задачу Коши Рассмотрим вспомогательную задачу Применяя операционный метод, находим По формуле (11) получаем решение x(t) исходной задачи: Интегрирование систем осуществляется так же, как и решение одного линейного дифференциального уравнения — путем перехода от системы дифференциальных уравнений к системе операторных уравнений. Решая последнюю как систему линейных алгебраических уравнений относительно изображений искомых функций, получаем операторное решение системы. Оригинал для негобудетрешением исходной системы дифференциальных уравнений. Пример: Найти решение линейной системы удовлетворяющее начальным условиям х(0) = у(0) = I. Пусть х( Решая последнюю относительно Х(р) и У(р), получаем Решение исходной задачи Коши Напомним, что интегральным уравнением называют уравнение, в котором неизвестная функция входит под знак интеграла. Мы рассмотрим лишь уравнение вида (12) называемое линейным интегральным уравнением Вольтерра второго рода с ядром K(t — т), зависящим от разности аргументов (уравнение типа свертки). Здесь φ(t) — искомая функция, f(t) и K(t) — заданные функции. Пусть f(t) и K(t) есть функции-оригиналы, f(t) =’ F(p), K(t) =’ K(p). Применяя к обеим частям (12) преобразование Лапласа и, пользуясь теоремой умножения, получим где Ф(р) = φ(t). Из (13) Оригинал для Ф(р) будет решением интегрального уравнения (12). Пример: Решить интегральное уравнение Применяя преобразование Лапласа к обеим частям (14), получим Функция Замечание: Преобразование Лапласа может быть использовано также при решении некоторых задач для уравнений математической физики. Решение заданий и задач по предметам: Дополнительные лекции по высшей математике: Образовательный сайт для студентов и школьников Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника. © Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института http://poisk-ru.ru/s18178t18.html http://lfirmal.com/preobrazovanie-laplasa/
(4)Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами
Решение интегральных уравнений
(13)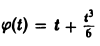
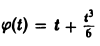
Таблица преобразования Лапласа
Дополнение к преобразованию Лапласа