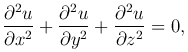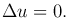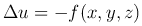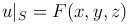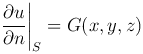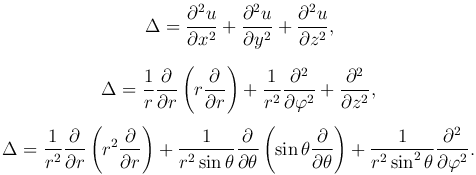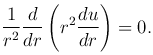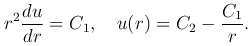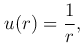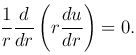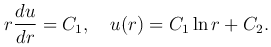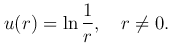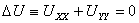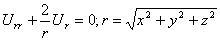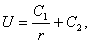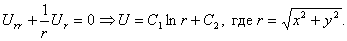Фундаментальное решение уравнения лапласа в пространстве

Уравнение Лапласа

Рассмотрим уравнение с частными производными вида

где u=u(x, y, z). Это уравнение называется уравнением Лапласа.

Левая часть обозначается Δu и называется оператором Лапласа. Таким образом, это уравнение преобразуется к виду:

Данному уравнению удовлетворяет потенциал скорости безвихревого течения несжимаемой (с постоянной плотностью) жидкости; потенциал сил тяготения или сил взаимодействия электрических зарядов во всех точках пространства, находящихся вне притягивающих масс или вне зарядов, создающих поле; температура в однородном теле, если теплообмен является стационарным, т.е. температура u зависит только от места, но не от времени и др.

называется уравнением Пуассона.

Уравнение Лапласа и уравнение Пуассона является уравнениями эллиптического типа.

Определение. Функцию, непрерывную в некоторой области вместе со своими частными производными до второго порядка включительно и удовлетворяющую уравнению Лапласа, называют гармонической.

Обычно в задачах, связанных с уравнением Лапласа или Пуассона, искомое решение должно удовлетворять уравнению в области D, а также некоторому дополнительному условию на границе S области D.

Если надо определить функцию, гармоническую в области D, когда на границе S области D заданы ее значения, т.е.

(первая краевая задача), то такая задача называется задачей Дирихле.

Если же надо определить функцию, гармоническую в области D, когда на границе S задается значение нормальной производной

(вторая краевая задача), то такая задача называется задачей Неймана.

Определение. Если решение задачи ищут в области D, внутренней (внешней) по отношению к поверхности S, то соответствующую задачу называют внутренней (внешней) краевой задачей.

Фундаментальные решения уравнения Лапласа

Рассмотрим уравнение Лапласа

где оператор Лапласа в декартовой, цилиндрической и сферической системах координат определяется соответственно

Важную роль при решении задач для уравненийй Лапласа и Пуассона представляют решения, обладающие сферической или цилиндрической симметрией.

Найдем решение уравнения Лапласа, удовлетворяющее условию сферической симметрии, когда функция u зависит только от расстояния 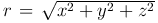точки M(x, y, z) до начала координат. В этом случае уравнение Лапласа в сферической системе координат имеет вид

Интегрируя это уравнение, получим

которая удовлетворяет уравнению Лапласа всюду, кроме точки r=0, где она обращается в бесконечность. Такую функцию называют фундаментальным решением уравнения Лапласа в пространстве.

В задаче с осевой симметрией, когда функция u в цилиндрической системы координат не зависит от φ и z, уравнение Лапласа имеет вид

Интегрируя это уравнение, получим

Эта функция называется фундаментальным решением уравнения Лапласа на плоскости.

Лекция 7. Гармонические функции и их свойства

Рассмотрим уравнение Лапласа на плоскости

и в пространстве

Уравнение (33) при переходе к полярным координатам преобразуется к виду

Рис 14 Рис 14.1

Если в пространстве перейти к сферическим координатам

то уравнение (34) примет вид

Функции U=U(x,y) на плоскости и U=U(x,y,z) в пространстве, имеющие непрерывные частные производные второго порядка и удовлетворяющие, соответственно, уравнению Лапласа (33) или (34) в некоторой области D, называются гармоническими в этой области. Простейшими примерами гармонических функций являются линейные функции: U = ах + by + с на плоскости и U = ax + by + cz + d в пространстве. Особый интерес представляют решения уравнения Лапласа, обладающие сферической или цилиндрической (в случае двух независимых переменных — круговой) симметрией.

Решение U=U(r), обладающее сферической симметрией, будет определяться из обыкновенного дифференциального уравнения

Это уравнение получится, если подставить искомую функцию в уравнение Лапласа (34*), записанное в сферических координатах. Интегрируя это уравнение, находим

где C₁ и C₂ — произвольные постоянные. Полагая C₁=1, C₂=0, получим функцию

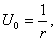
которую часто называют фундаментальным решением уравнения Лапласа в пространстве. Функция U₀ является гармонической всюду в пространстве, кроме начала координат 0.

Аналогично, полагая U=U(r) и пользуясь уравнением Лапласа в цилиндрических или полярных координатах, найдем решения, обладающие цилиндрической или круговой симметрией:

Выбирая С₁=-1 и С₂=0, будем иметь функцию

Рассмотрим в пространстве электрическое поле, образованное точечным зарядом величины q , помещенным в начало координат. Тогда потенциал этого поля равен

Аналогично, если рассмотреть поле, создаваемое заряженной прямой, то потенциал такого поля будет равен

где q₁ — линейная плотность заряда (то есть заряд, рассчитанный на единицу длины).

Более сложные примеры будут рассмотрены далее, а сейчас изучим свойства гармонических функций.

Теорема о среднем. Пусть функция U=U(x,y) гармоническая в некотором круге D радиуса R с центром (х_o,у_o) и непрерывная в соответствующем замкнутом круге Тогда значение этой функции в центре круга равно ее среднему значению на окружности Г, ограничивающей данный круг, то есть

При доказательстве этой теоремы применим интегральную формулу Пуассона для круга, которая будет доказана позже в лекции 10. Она имеет вид (см. рис. 15)

Если в этой формуле положить ρ=0, то получится формула (35).

Теорему о среднем можно представить и в другой форме. Для этого запишем формулу (35) для произвольного круга радиуса r, где 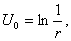(см. рис.15.1):

Умножив обе части равенства (36) на rdr и проинтегрировав по r в пределах от 0 до R, получим:

где D — круг радиуса R. Разделив обе части полученного равенства на R 2 /2 , будем иметь

В правой части формулы (37) записано среднее значение гармонической функции U(x,y) в круге радиуса R.

Имеет место и обратная теорема: если в некоторой области D функция U=U(x,y) непрерывная и для каждой точки выполняется теорема о среднем в любом сколь угодно малом круге с центром в точке (х_о, у_о), то эта функция гармоническая в D. Из формулы (37) получается:

Следствие. Если функция U=U(x,y) гармоническая в некотором круге D радиуса R и непрерывная в соответствующем замкнутом круге ,то

Число называют нормой функции U=U(x,y) в области D , и неравенство (38) можно переписать в виде

Неравенство (38) доказывается совсем просто, если воспользоваться известным неравенством Коши-Буняковского:

Применим это неравенство к формуле (37):

Что и требовалось доказать.

Гармонические функции, помимио вышеуказанных свойств, обладают и многими другими свойствами. Приведем еще два из них.

Неравенство Харнака. Пусть функция гармоническая в некотором круге D радиуса R c центром (x_o, у_o) и непрерывная в соответствующем круге Тогда при любом она удовлетворяет неравенству

Из неравенства Харнака следует теорема Лиувилля.

Теорема Лиувилля. Гармоническая на всей плоскости функция U=U(x, у) не может быть ограниченной сверху или снизу, если она не постоянная.

Доказательство. Если функция U=U(x, у) ограничена сверху, то U₁=-U(x, y) — ограничена снизу и тоже гармоническая. Поэтому достаточно рассмотреть случай, когда функция ограничена снизу: Более того, можно считать, что M=0. Действительно, ,а разность (U-M) тоже гармоническая функция. Итак, предполагая существование гармонической во всей плоскости неотрицательной функции U(x, у), мы докажем, что эта функция постоянная.

Воспользуемся неравенством Харнака

Если функция U(x, у) гармоническая во всей плоскости то, фиксировав произвольное и неограниченно увеличивая R мы получим

то есть Теорема Лиувилля доказана.

Замечание. Гармонические функции в пространстве обладают аналогичными свойсвами. Приведем формулировку одного из них.

Терема о среднем. Пусть функция U=U(x, у) гармоническая в некотором шаре D радиуса R c центром
(x_o , у_o , z_o ) и непрерывная в соответствующем замкнутом шаре Тогда значение этой функции в центре шара равно:

а) ее среднему значению на сфере Г, ограничивающей данный шар, то есть

б) ее среднему значению в шаре D, то есть

Боковая панель

Полное и подробное, насколько это возможно, решение уравнения Лапласа в сферических координатах, приводящее к шаровым и сферическим функциям. Всё самое интересное на, хоть и длинной, но одной странице. Много математики — много веселья!

Эту запись можно посмотреть в nbviewer.

Уравнение Лапласа в сферических координатах

Уравнение Лапласа в сферических координатах имеет вид

где $ r, \vartheta = 90^\circ — \varphi, \lambda $ — радиус, полярное расстояние (дополнение широты $\varphi$ до $90^\circ$), долгота соответственно.

Решить уравнение Лапласа это значит найти конкретный вид гармонической функции $f \left( r, \vartheta, \lambda \right)$, удовлетворяющей ему.

Прежде, чем переходить к решению, заметим важное и полезное свойство уравнения Лапласа: оно линейно. Это означает, что если есть два решения этого уравнения $f_1$ и $f_2$, то есть

$$ \Delta f_1 = 0,\qquad \Delta f_2 = 0, $$

то их линейная комбинация

$$ f = \alpha f_1 + \beta f_2 $$

тоже является решением $\Delta f = 0$.

Разделение переменных

Будем искать решение уравнения Лапласа методом разделения переменных, суть которого в следующем. Представим искомую функцию $f$ трёх переменных $r, \vartheta, \lambda$ как произведение трёх других функций

\begin f \left(r, \vartheta, \lambda \right) = R(r) \cdot \Theta \left( \vartheta \right) \cdot \Lambda \left( \lambda \right), \end

каждая из которых теперь зависит только от одной переменной: $R$ есть функция только от $r$, $\Theta$ есть функция только от $\vartheta$, а $\Lambda$ есть функция только от $\lambda$. Стоит заметить, что не всякая система координат позволяет решить уравнение Лапласа методом разделения переменных, например этого нельзя сделать в геодезических координатах $H, B, L$.

Итак, делаем подстановку

Замечаем, что частные производные заменены на полные дифференциалы, поскольку функции $R, \Theta, \Lambda$ имеют только одну переменную. Разделим обе части уравнения на $R\Theta\Lambda$ и умножим на $r^2$:

Первый член уравнения зависит только от $r$, а вся оставшаяся часть зависит только от угловых величин $\vartheta, \lambda$. Для того, чтобы равенство выполнялось необходимо, чтобы обе части равнялись некоторой постоянной $\alpha$:

Первое уравнение будем называть радиальной частью уравнения Лапласа, поскольку она зависит только от $r$. Оставшуюся часть умножим на $\sin^<2><\left(\vartheta \right)>$ и запишем уравнение

которое является угловой частью уравнения Лапласа и называется дифференциальным уравнением сферических функций, поскольку, как увидим позже, именно они будут его решением.

И снова становится очевидным, что для сохранения равенства в полученном уравнении необходимо, чтобы обе части равнялись некоторой постоянной $\beta$:

Таким образом, уравнение Лапласа, дифференциальное уравнение в частных производных второго порядка, разбивается на три обыкновенных дифференциальных уравнения второго порядка:

$$ \begin r^2 \frac R>> + 2 r \frac — \alpha R &= 0, \label \tag<1>\\ \frac<1> <\Theta>\frac \Theta>> + \frac<1>< \tan<\left(\vartheta \right)>> \frac— \alpha \Theta \sin^<2><\left(\vartheta \right)>— \dfrac<\beta \Theta><\sin<\vartheta>> &= 0, \label \tag <2>\\ \frac\Lambda>> + \beta \Lambda &= 0. \label \tag <3>\end $$ Нам требуется теперь решить каждое из уравнений в отдельности, а заодно и определить вид постоянных $\alpha$ и $\beta$.

Отметим, что угловая часть уравнения Лапласа $Y (\vartheta, \lambda) = \Theta (\vartheta) \Lambda (\lambda)$ зависит только от полярного расстояния $\vartheta$ и долготы $\lambda$, то есть явялется функцией, заданной на сфере, следовательно решение этой части должно быть периодическим: $\pi$ для широтной части и $2\pi$ для долготной части. Только при этих условиях функция $Y (\vartheta, \lambda)$ может быть однозначно заданной на сфере.

Уравнение гармонических колебаний

Обыкновенное дифференциальное уравнение второго порядка вида

называется уравнением гармонических (или свободных) колебаний.

Оно имеет два линейно независимых решения при $\beta > 0$

что легко проверяется подстановкой.

Как уже было сказано выше, для того, чтобы функция $Y \left( \vartheta, \lambda \right)$ была однозначной на сфере, необходимо, чтобы функция $\Lambda$ имела период $2\pi$. Из последнего уравнения нетрудно установить, что такое возможно только при $\beta = m^2$, $m = 0, 1, 2, …$ Таким образом, решения уравнения гармонических колебаний принимают вид

линейная комбинация которых

является общим решением дифференциального уравнения. Здесь $C_1$ и $C_2$ — произвольные константы.

Присоединённое уравнение Лежандра

Перепишем второе уравнение, подставив в него значение $\beta = m^2$:

И подставляя всё это, получим уравнение без тригонометрических функций в явном виде:

$$ \left( 1 — t^2 \right) \dfrac— 2 t \dfrac