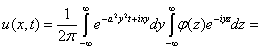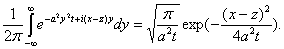Фундаментальное решение уравнения теплопроводности и его физический смысл

Фундаментальное решение уравнения теплопроводности; его физический смысл

Нестационарное урав­нение теплопроводности в неподвижной среде в декартовой системе координат имеет вид:

. (1)

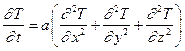
Рассмотрим безграничное пространство, заполненное однородной не­по­движ­ной сре­дой с плотностью r, теплоемкостью c и коэффициентом тем­пе­ра­ту­ро­про­вод­ности a. Пусть в этом пространстве в точ­ке с координатами x’, y’, z’ в момент времени t’ сработал (включился и сразу же выключился) мгновенный источник тепла, выделивший количество те­п­ла, равное Q. Тогда температура в любой точке с координатами x, y, z в любой момент времени t > t’ может быть определена по формуле

. (2)

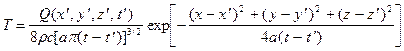
Функция (2) ввиду ее чрезвычайной важности для приложений называется фун­да­мен­таль­ным ре­ше­нием уравнения теплопроводности. В том, что эта фун­к­ция является ре­ше­ни­ем уравнения теплопроводности (1), проще всего убе­дить­ся непосредственной проверкой. Про­диф­фе­рен­ци­руем фундаментальное ре­шение один раз по t и дважды по x, y, z:

,

, ,

.

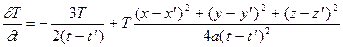
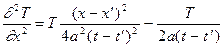
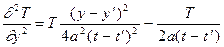
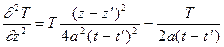
Подставляя эти формулы в уравнение (1), убеждаемся, что при t > t’ получается тождество.

На первый взгляд может показаться, что практическая польза от фун­да­мен­таль­ного ре­ше­ния невелика, т.к. мгновенных то­чечных источников в при­ро­де и в тех­нике не существует; лю­бой реальный ис­точ­ник имеет конечные раз­ме­ры и дей­ст­ву­ет в течение конечного про­ме­жут­ка вре­ме­ни. Однако всегда мож­но мысленно раз­бить источник теп­ла на отдельные эле­мен­ты, на­столь­ко малые, чтобы их можно бы­ло счи­тать точечными, и, используя прин­цип су­пер­по­зиции, сложить температуры, создаваемые эти­ми эле­ментами (другими словами, про­ин­те­гри­ровать фундаментальное ре­ше­ние по координатам x’, y’, z’ в пре­де­лах ре­альных размеров ис­точника). Аналогично, отрезок времени, в течение ко­то­ро­го дейст­во­вал источник, можно раз­бить на множество бесконечно малых ин­тер­валов dt’ и проинтегрировать фундаментальное ре­шение по t’ от момента вклю­чения до момента выключения источника. При этом можно учесть, что раз­личные элементы источника могут иметь различную мощность, которая к то­му же может меняться со временем, т.е. решить множество практически важ­ных задач. Если ис­точ­ники тепла имеют сложную форму, и (или) их мощность ме­няется сложным образом, так что получить аналитическое решение не уда­ет­ся, можно применить методы численного ин­тег­ри­рования. Простейшие при­ме­ры применения этих идей приведены ниже. Кроме то­го, в некоторых случаях, ко­гда мощный источник тепла действовал непродолжительное вре­мя, на рас­сто­яниях, много больших, чем размеры источника, можно непосредственно ис­поль­зо­вать формулу (2). В качестве примера можно назвать подземный взрыв (обычный или ядерный небольшой мощности), про­из­ве­ден­ный на боль­шой глубине.

Рассмотрим некоторые свойства фундаментального решения. Если начало координат поместить в точку (x’, y’, z’) а отсчет времени начать с момента t’, то вид формулы (2) значительно упрощается:

, (3)

где r 2 = x 2 + y 2 + z 2 — квадрат расстояния от источника (от начала координат) до точки на­блю­де­ния. Если зафиксировать ряд моментов времени 0 2 /(6a). В этот момент тем­пе­ратура в точке, находящейся на расстоянии r от мгновенного точечного источника достигает мак­симума.

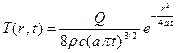
Компьютерный чертеж. Выполним

Распространение тепла в неограниченном стержне. Фундаментальное решение уравнения теплопроводности

Для решения краевых задач математической физики широко применяется преобразование Фурье. Причина этого заключается в том, что образ Фурье искомой функции часто удовлетворяет более простому уравнению, чем сама искомая функция. При решении краевых задач математической физики преобразование Фурье используется по следующей схеме:

1. Подвергают преобразованию Фурье обе части уравнения, которому удовлетворяет искомая функция; отсюда получают уравнение для ее Фурье-образа;

2. Из этого уравнения находят образ Фурье искомого решения первоначального уравнения;

3. Используя обратное преобразование Фурье находят искомую функцию.

Рассмотрим распределение температуры в неограниченном в обе стороны прямолинейном стержне в произвольный момент времени , если ее распределение в начальный момент времени известно. Стержень считаем теплоизолированным от окружающей среды по боковой поверхности и его сечение считаем настолько малым, что всем точкам сечения в каждый момент времени можно приписать одну и ту же температуру.

Задача заключается в нахождении решения уравнения теплопроводности в бесконечной области по известному начальному условию:

где – заданная функция, абсолютно интегрируемая на оси .

Решаем эту задачу, применяя преобразование Фурье по переменной x. Обозначим через образ Фурье функции

Умножим обе части уравнения (2) на и проинтегрируем по от до , предполагая, что функция и ее производные достаточно быстро стремятся к нулю при . Интегрируя левую часть, получим

Для преобразования правой части уравнения используем интегрирование по частям:

При получении (6) учли, что неинтегральные члены обращаются в нуль, в силу ограниченности функции и предполагаемого поведения функции :

Приравнивая (5) и (6), получим обыкновенное дифференциальное уравнение для образа Фурье искомой функции

Начальное условие для функции получим из начального условия (3), выполнив преобразование Фурье

Разделяя переменные в уравнении (7), получаем

Определим постоянную С с помощью начального условия (8)

Подставив это значение С в равенство (9), получим для Фурье-образа искомой функции следующее выражение

Теперь осталось перейти к третьему этапу решения задачи — найти саму функцию по найденному ее образу Фурье (10). Для этого применим к равенству (10) обратное преобразование Фурье, подставив вместо его явное выражение из (8). Умножив (10) на и интегрируя по , получаем

Подставим в правую часть выражение для экспоненты с мнимым аргументом по формуле Эйлера

если — четная функция, а также равенство ,

если — нечетная функция, имеем

Последний интеграл является известной и часто встречающейся в теории теплопроводности и теории диффузии функцией. Воспользуемся формулой

Подставив эти результаты в выражение (11), получим решение уравнения (2) при начальном условии (3)

Полученную формулу называют формулой Пуассона. Функция аргументов и

называется фундаментальным решением уравнения теплопроводности (2). Она удовлетворяет уравнению теплопроводности. Решение уравнения теплопроводности с начальным условием в виде (12) является сверткой фундаментального решения с начальной функцией.

Рассмотрим физический смысл фундаментального решения уравнения теплопроводности. Выделим малый элемент стержня вблизи точки и зададим начальное распределение температуры в виде

Физически это означает, что в начальный момент времени этому элементу стержня передали количества тепла ( — линейная плотность материала, — удельная теплоемкость), которое привело к повышению температуры на этом элементе на величину . В последующие моменты времени распределение температуры в стержне определяется формулой (12), которая в данном случае принимает вид

Если распределять то же самое количество тепла Q на все меньшем участке , то в пределе в точке стержню сообщается количества тепла Q. Это означает, что в точке стержня в момент действует мгновенный точечный источник тепла напряжения Q. От действия такого мгновенного точечного источника тепла в стержне получается распределение температур

где применена теорема о среднем для определенного интеграла

Предел последнего выражения при , а значит , и приводит к выражению (14).

Таким образом, фундаментальное решение (13) дает распределение температуры, которое вызывается мгновенным точечным источником тепла напряжения , помещенным в начальный момент времени в точке стержня.

В соответствии с этим можно дать физическое толкование и решению (12). Для того, чтобы придать сечению стержня температуру в начальный момент времени, мы должны на малом элементе около этой точки распределить количество тепла , т. е. поместить в точке мгновенный точечный источник тепла напряжения . Распределение температуры, вызываемое этим мгновенным точечным источником будет равно

Общее действие от начальной температуры во всех точках стержня складывается от этих элементов, что и приводит к формуле (12).

Фундаментальное решение уравнения теплопроводности.

Преобразуем формулу 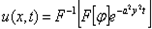к более удобному ”явному” виду. Для этого запишем ее в интегралах

меняем порядок интегрирования

(4.1)

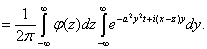
В формуле (4.1) внутренний интеграл есть преобразование Фурье от функции 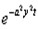при значении аргумента –(x-z), поэтому имеем

Подставляя это в (4.1), получим

(4.2)

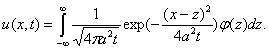
называют фундаментальным решением уравнения теплопроводности

В заключение хотелось бы отметить, что о Фурье мы прежде всего вспоминаем как об авторе “Аналитической теории теплоты” (1822 г.). В силу общности метода эта книга стала источником всех современных методов математической физики, относящихся к интегрированию уравнений в частных производных при заданных граничных условиях.

Дата добавления: 2015-06-10 ; просмотров: 1186 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ