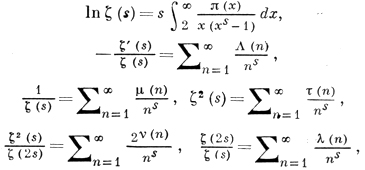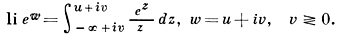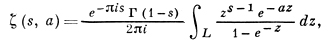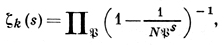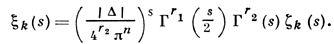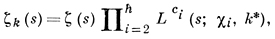Функциональное уравнение дзета функции римана

Доступное объяснение гипотезы Римана

Посвящается памяти Джона Форбса Нэша-младшего

Вы ведь помните, что такое «простые числа»? Эти числа не делятся ни на какие другие, кроме самих себя и 1. А теперь я задам вопрос, которому уже 3000 лет:

• 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, p. Чему равно p? 31. Каким будет следующее p? 37. А следующее p ? 41. А следующее? 43. Да, но… как нам узнать, каким будет следующее значение?

Придумайте суждение или формулу, которые (хотя бы с грехом пополам) прогнозируют, каким будет следующее простое число, (в любом заданном ряду чисел), и ваше имя навечно будет связано с одним из величайших достижений человеческого мозга. Вы встанете в один ряд с Ньютоном, Эйнштейном и Гёделем. Разберитесь в поведении простых чисел, и можете потом всю жизнь почивать на лаврах.

Введение

Свойства простых чисел изучались многими великими людьми в истории математики. С первого доказательства бесконечности простых чисел Евклида до формулы произведения Эйлера, связавшей простые числа с дзета-функцией. От формулировки теоремы о простых числах Гаусса и Лежандра до её доказательства, придуманного Адамаром и Валле-Пуссеном. Тем не менее, Бернхард Риман до сих пор считается математиком, сделавшим единственное крупнейшее открытие в теории простых чисел. В его опубликованной в 1859 году статье, состоявшей всего из восьми страниц, были сделаны новые, ранее неизвестные открытия о распределении простых чисел. Эта статья по сей день считается одной из самых важных в теории чисел.

После публикации статья Римана оставалась главным трудом в теории простых чисел и на самом деле стала основной причиной доказательства в 1896 году теоремы о распределении простых чисел. С тех пор было найдено несколько новых доказательств, в том числе элементарные доказательства Сельберга и Эрдёша. Однако до сих пор остаётся загадкой гипотеза Римана о корнях дзета-функции.

Сколько всего простых чисел?

Давайте начнём с простого. Все мы знаем, что число является или простым, или составным. Все составные числа состоят из простых и могут быть разложены на их произведения (a x b). В этом смысле простые числа являются «строительными блоками» или «фундаментальными элементами» чисел. В 300 году до нашей эры Евклид доказал, что их количество бесконечно. Его изящное доказательство имеет следующий вид:

Предположим, что множество простых чисел не бесконечно. Создадим список всех простых чисел. Тогда P пусть будет произведением всех простых чисел списка (перемножим все простые числа из списка). Прибавим к результату 1: Q = P +1. Как и все числа, это натуральное число Q должно быть или простым, или составным:

• Если Q простое, то мы нашли простое число, которого нет в нашем «списке всех простых чисел».
• Если Q не простое, то оно составное, т.е. составлено из простых чисел, одно из которых, p, будет делителем Q (потому что все составные числа являются произведениями простых). Каждое простое p, из которого составлено P, очевидно является делителем P. Если p является делителем и для P, и для Q, то оно должно быть и делителем для их разности, то есть единицы. Ни одно простое число не является делителем 1, поэтому число p не может находиться в списке — ещё одно противоречие тому, что список содержит все простые числа. Всегда будет существовать ещё одно простое p, не находящееся в списке и являющееся делителем Q. Следовательно, простых чисел бесконечно много.

Почему простые числа так сложно понять?

Сам факт того, что любой новичок понимает изложенную выше задачу, красноречиво говорит о её сложности. Даже арифметические свойства простых чисел, несмотря на активное изучение, плохо нами понимаются. Научное сообщество настолько уверено в нашей неспособности понимать поведение простых чисел, что разложение на множители больших чисел (определение двух простых чисел, произведением которых является число) остаётся одной из фундаментальных основ теории шифрования. На это можно смотреть следующим образом:

Мы хорошо понимаем составные числа. Это все числа, не являющиеся простыми. Они состоят из простых чисел, но мы можем с лёгкостью написать формулу, прогнозирующую и/или генерирующую составные числа. Такой «фильтр составных чисел» называется решетом. Самым знаменитым примером является так называемое «решето Эратосфена», придуманное примерно в 200 году до нашей эры. Его работа заключается в том, что оно просто помечает значения, кратные каждому простому числу вплоть до заданной границы. Допустим, возьмём простое число 2, и пометим 4,6,8,10, и так далее. Затем возьмём 3, и пометим 6,9,12,15, и так далее. В результате у нас останутся только простые числа. Хоть его очень легко понять, решето Эратосфена, как вы можете представить, не особо эффективно.

Одной из функций, серьёзно упрощающих нашу работу, будет 6n ± 1. Эта простая функция выдаёт все простые числа, за исключением 2 и 3, и удаляет все числа, кратные 3, а также все чётные числа. Подставим n = 1,2,3,4,5,6,7 и получим следующие результаты: 5,7,11,13,17,19,23,25,29,31,35,37,41,43. Единственными не простыми числами, сгенерированными функцией, являются 25 и 35, которые можно разложить на множители 5 x 5 и 5 x 7. Следующими не простыми числами, как вы могли догадаться, будут, 49 = 7 x 7, 55 = 5 x 11, и так далее. Всё легко, правда?

Для визуального отображения этого я использовал то, что называю «лестницей составных чисел» — удобный способ показать, как расположены и сочетаются сгенерированные функцией составные числа. В первых трёх столбцах показанного ниже изображения мы видим, как красиво поднимаются по каждой лестнице составных чисел простые числа 5, 7 и 11, вплоть до значения 91. Хаос, возникающий в четвёртом столбце, показывающем, как решето убрало всё, кроме простых чисел — отличная иллюстрация того, почему простые числа так сложно понять.

Фундаментальные ресурсы

Как же это всё связано с понятием, о котором вы могли слышать — с «гипотезой Римана»? Ну если говорить просто, то чтобы больше понять о простых числах, математики в 19-м веке перестали пытаться спрогнозировать местонахождение простых чисел с абсолютной точностью, и вместо этого начали рассматривать феномен простых чисел в целом. Мастером этого аналитического подхода стал Риман, и в рамках такого подхода была создана его знаменитая гипотеза. Однако прежде чем я начну её объяснять, необходимо познакомиться с некоторыми фундаментальными ресурсами.

Гармонические ряды

Гармонические ряды — это бесконечные ряды чисел, которые впервые исследовал в 14-м веке Николай Орем. Его имя связано с концепцией музыкальных гармоник — обертонов, которые выше частоты основного тона. Ряды имеют следующий вид:

Первые члены бесконечного гармонического ряда

Орем доказал, что эта сумма является несходящейся (то есть не имеющей конечного предела; она не приближается и не стремится к какому-то определённому числу, а устремлена в бесконечность).

Дзета-функции

Гармонические ряды являются особым случаем более общего типа функций под названием дзета-функция ζ(s). Вещественная дзета-функция задаётся для двух вещественных чисел r и n:

Если подставить n = 1, то мы получим гармонический ряд, который расходится. Однако при всех значениях n > 1 ряд сходится, то есть сумма при увеличении r стремится к некому числу, а не уходит в бесконечность.

Формула произведения Эйлера

Первая связь между дзета-функциями и простыми числами была установлена Эйлером, когда он показал, что для двух натуральных (целочисленных и больше нуля) чисел n и p, где p является простым, справедливо следующее:

Произведение Эйлера для двух чисел n и p, где оба больше нуля, а p является простым.

Это выражение впервые появилось в статье 1737 года под названием Variae observationes circa series infinitas. Из выражения следует, что сумма дзета-функции равна произведению величин, обратной единице, минус величина, обратная простым числам в степени s. Эта потрясающая связь заложила фундамент современной теории простых чисел, в которой с тех пор дзета-функция ζ(s) начала использоваться как способ изучения простых чисел.

Доказательство формулы — это одно из самых любимых моих доказательств, поэтому я изложу его, хоть для наших целей это и не обязательно (но настолько же оно прекрасно!):

Доказательство формулы произведения Эйлера

Эйлер начинает с общей дзета-функции

Сначала он умножает обе части на второй член:

Дзета-функция, умноженная на 1/2 s

Затем он вычитает получившееся выражение из дзета-функции:

Дзета-функция минус 1/2 s , умноженное на дзета-функцию

Он повторяет этот процесс, далее умножая обе стороны на третий член

Дзета-функция минус 1/2 s , умноженное на дзета-функцию, умноженное на 1/3 s

А затем вычитает получившееся выражение из дзета-функции

Дзета-функция минус 1/2 s , умноженное на дзета-функцию минус 1/3 s , умноженное на дзета-функцию

Если повторять этот процесс до бесконечности, в конце концов у нас останется выражение:

1 минус все величины, обратные простым числам, умноженное на дзета-функцию

Если этот процесс вам знаком, то это потому, что Эйлер по сути создал решето, очень похожее на решето Эратосфена. Он отфильтровывает из дзета-функции числа, не являющиеся простыми.

Затем разделим выражение на все его члены, являющимися обратными простым числам величинами, и получим:

Функциональная связь дзета-функции с простыми числами для первых простых чисел 2,3,5,7 и 11

Упростив выражение, мы показали следующее:

Формула произведения Эйлера — равенство, показывающее связь между простыми числами и дзета-функцией

Разве это было не красиво? Подставим s = 1, и найдём бесконечный гармонический ряд, повторно доказав бесконечность простых чисел.

Функция Мёбиуса

Август Фердинанд Мёбиус переписал произведение Эйлера, создав новую сумму. Кроме величин, обратных простым числам, функция Мёбиуса также содержит каждое натуральное число, являющееся произведением чётного и нечётного количества простых множителей. Числа, исключённые из его ряда — это такие числа, которые делятся на какое-то простое число в квадрате. Его сумма, обозначаемая как μ(n), имеет следующий вид:

Функция Мёбиуса — изменённая версия произведения Эйлера, заданная для всех натуральных чисел

Сумма содержит величины, обратные:

1. Каждому простому числу;
2. Каждому натуральному числу, являющемуся произведением нечётного количества разных простых чисел, взятому со знаком «минус»; и
3. Каждому натуральному числу, являющемуся произведением чётного количества различных простых чисел, взятому со знаком «плюс»;

Ниже показаны первые члены:

Ряд/сумма единиц, разделённых на дзета-функцию ζ(s)

Сумма не содержит те обратные величины, которые делятся на квадрат одного из простых чисел, например, 4,8,9, и так далее.

Функция Мёбиуса μ(n) может принимать только три возможных значения: префикс (1 или -1) или удаление (0) членов из суммы:

Три возможных значения функции Мёбиуса μ(n)

Хотя впервые эта хитрая сумма была формально определена Мёбиусом, примечательно, что за 30 лет до него об этой сумме писал в заметках на полях Гаусс:

«Сумма всех первообразных корней (простого числа p) или ≡ 0 (когда p-1 делится на квадрат), или ≡ ±1 (mod p) (когда p-1 является произведением неравных простых чисел); если их количество чётно, то знак положителен, но если количество нечётно, то знак отрицателен».

Функция распределения простых чисел

Вернёмся к простым числам. Чтобы понять, как распределяются простые числа при движении вверх по числовой прямой, не зная точно, где они находятся, полезно будет подсчитать, сколько их встречается до определённого числа.

Именно эту задачу выполняет предложенная Гауссом функция распределения простых чисел π(x): она даёт нам количество простых чисел, меньших или равных заданному вещественному числу. Поскольку мы не знаем формул для нахождения простых чисел, формула распределения простых чисел известна нам только как график, или ступенчатая функция, увеличивающаяся на 1, когда x является простым числом. На графике ниже показана функция до x = 200.

Функция распределения простых чисел π(x) до значения x = 200.

Теорема о распределении простых чисел

Теорема о распределении простых чисел, сформулированная Гауссом (и независимо от него Лежандром), гласит:

Теорема о распределении простых чисел

Обычным языком это можно изложить так: «При движении x к бесконечности функция распределения простых чисел π(x) будет приближаться к функции x/ln(x)». Другими словами, если забраться достаточно далеко, и график распределения простых чисел поднимется до очень высокого числа x, то при делении x на натуральный логарифм x соотношение этих двух функций будет стремиться к 1. Ниже на графике показаны две функции для x = 1000:

Функция распределения простых чисел π(x) и приблизительная оценка по теореме распределения простых чисел до x = 1000

С точки зрения вероятностей, теорема о распределении простых чисел гласит, что если случайным образом выбрать натуральное число x, то вероятность P(x) того, что это число будет простым, примерно равно 1 / ln(x). Это означает, что средний разрыв между последовательными простыми числами среди первых x целочисленных значений приблизительно равен ln(x).

Интегральный логарифм

Функция Li(x) определена для всех положительных вещественных чисел, за исключением x = 1. Она задаётся интегралом от 2 до x:

Интегральное представление функции интегрального логарифма

Построив график этой функции рядом с функцией распределения простых чисел и формулой из теоремы о распределении простых чисел, мы видим, что Li(x) на самом деле является лучшим приближением, чем x/ln(x):

Интегральный логарифм Li(x), функция рапределения простых чисел π(x) и x/ln(x) на одном графике

Чтобы узнать, насколько лучше это приближение, мы можем построить таблицу с большими значениями x, количеством простых чисел до x и величиной погрешности между старой (теорема о распределении простых чисел) и новой (интегральный логарифм) функциями:

Количество простых чисел до заданной степени десятки и соответствующие погрешности для двух приближений

Как легко можно заметить, интегральный логарифм намного лучше в приближении, чем функция из теоремы о распределении простых чисел, он «ошибся» в большую сторону всего на 314 890 простых чисел для x = 10 в степени 14. Тем не менее, обе функции сходятся к функции распределения простых чисел π(x). Li(x) сходится гораздо быстрее, но при стремлении x к бесконечности соотношение между функцией распределения простых чисел и функциями Li(x) и x/ln(x) приближается к 1. Покажем это наглядно:

Схождение соотношений двух приближенных значений и функции распределения простых чисел к 1 при x = 10 000

Гамма-функция

Гамма-функция Γ(z) стала важным объектом для изучения с тех пор, когда в 1720-х годах Даниил Бернулли и Христиан Гольдбах исследовали задачу обобщения функции факториала на нецелые аргументы. Это обобщение функции факториала n! (1 x 2 x 3 x 4 x 5 x …. n), сдвинутое вниз на 1:

Гамма-функция, определённая для z

Её график очень любопытен:

График гамма-функции Γ(z) в интервале -6 ≤ z ≤ 6

Гамма-функция Γ(z) определена для всех комплексных значений z больше нуля. Как вы наверно знаете, комплексные числа — это класс чисел с мнимой частью, записываемых как Re(z) + Im(z), где Re(z) — это вещественная часть (обычное вещественное число), а Im(z) — мнимая часть, обозначаемая буквой i. Комплексное число обычно записывается в виде z = σ + it, где сигма σ — вещественная часть, а it — мнимая. Комплексные числа полезны тем, что они позволяют математикам и инженерам работать с задачами, недоступными обычным вещественным числам. В графическом виде комплексные числа расширяют традиционную одномерную числовую прямую в двухмерную числовую плоскость, называемую комплексной плоскостью, в которой вещественная часть комплексного числа откладывается по оси x, а мнимая — по оси y.

Чтобы гамма-функцию Γ(z) можно было использовать, её обычно переписывают в виде

Функциональная связь гамма-функции Γ(z)

С помощью этого равенства мы можем получить значения для z ниже нуля. Однако оно не даёт значений для отрицательных целых чисел, потому что они не определены (формально они являются вырожденностями или простыми полюсами).

Дзета и гамма

Связь между дзета-функцией и гамма-функцией задаётся следующим интегралом:

Дзета-функция Римана

Ознакомившись со всеми необходимыми фундаментальными ресурсами, мы можем наконец приступать к установлению связи между простыми числами и гипотезой Римана.

Немецкий математик Бернхард Риман родился в 1826 году в Брезеленце. Будучи студентом Гаусса, Риман опубликовал работу в области математического анализа и геометрии. Считается, что наибольший вклад он внёс в области дифференциальной геометрии, где заложил фундамент языка геометрии, позже использованного Эйнштейном в общей теории относительности.

Его единственный труд в теории чисел, статья 1859 года Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse («О простых числах меньше заданной величины») считается самой важной статьёй в этой области математики. Всего на четырёх страницах он изложил:

• Определение дзета-функции Римана ζ(s) — дзета-функции с комплексными значениями;
• Аналитическое продолжение дзета-функции на все комплексные числа s≠1;
• Определение кси-функции Римана ξ(s) — целой функции, связанной с дзета-функцией Римана через гамма-функцию;
• Два доказательства функционального уравнения дзета-функции Римана;
• Определение функции распределения простых чисел Римана J(x) с помощью функции распределения простых чисел и функции Мёбиуса;
• Явную формулу количества простых чисел меньше заданного числа с использованием функции распределения простых чисел Римана, определённой с помощью нетривиальных нулей дзета-функции Римана.

Это невероятный пример изобретательности и творческого мышления, подобных которому, вероятно, с тех пор не встречалось. Совершенно потрясающий труд.

Дзета-функция Римана

Мы видели тесную связь между простыми числами и дзета-функцией, показанную Эйлером в его произведении. Однако за исключением этой связи об их взаимоотношениях было мало что известно, и чтобы показать их, потребовалось изобретение комплексных чисел.

Риман первым рассмотрел дзета-функцию ζ(s) для комплексной переменной s, где s = σ + it.

Дзета-функция Римана для n, где s = σ + it — это комплексное число, в котором σ и t являются вещественными числами.

Этот бесконечный ряд, названный дзетой-функцией Римана ζ(s), является аналитическим (то есть имеет определяемые значения) для всех комплексных чисел с вещественной частью больше 1 (Re(s) > 1). В этой области определения он сходится абсолютно.

Чтобы проанализировать функцию в областях за пределами обычной области сходимости (когда вещественная часть комплексной переменной s больше 1), функцию нужно переопределить. Риман успешно с этим справился, выполнив аналитическое продолжение до абсолютно сходящейся функции на полуплоскости Re(s) > 0.

Переписанный вид дзета-функции Римана, где = x — |x|

Это новое определение дзета-функции аналитично в любой части полуплоскости Re(s) > 0, за исключением s = 1, где она является вырожденностью/простым полюсом. В этой области определения она называется мероморфной функцией, потому что она голоморфна (комплексно дифференцируема в окрестности каждой точки в области её определения), за исключением простого полюса s = 1. Кроме того, она является превосходным примером L-функции Дирихле.

В своей статье Риман на этом не остановился. Он перешёл к аналитическому продолжению своей дзета-функции ζ(s) на всю комплексную плоскость, воспользовавшись гамма-функцией Γ(z). Чтобы не усложнять пост, я не буду приводить эти вычисления, но крайне рекомендую вам посмотреть их самостоятельно, чтобы убедиться в удивительной интуиции и мастерстве Римана.

В его методе используется интегральное представление гаммы Γ(z) для комплексных переменных и тета-функции Якоби ϑ(x), которые можно переписать таким образом, чтобы появилась дзета-функция. Решая относительно дзета, получаем:

Функциональное уравнение дзеты для всей комплексной плоскости за исключением двух вырожденностей при s = 0 и s = 1

В таком виде мы замечаем, что член ψ(s) уменьшается быстрее чем любая степень x, а значит, интеграл сходится ко всем значениям s.

Зайдя ещё дальше, Риман заметил, что первый член в скобках (-1 / s(1 — s) ) является инвариантом (не меняется), если заменить s на 1 — s. Благодаря этому Риман ещё больше расширил полезность уравнения, устранив два полюса в s=0 и s=1, и задав кси-функцию Римана ξ(s) без вырожденностей:

Кси-функция Римана ξ(s)

Нули дзета-функции Римана

Корни/нули дзета-функции, когда ζ(s)=0, можно разделить на два вида, которые называются «тривиальными» и «нетривиальными» нулями дзета-функции Римана.

Существование нулей с вещественной частью Re(s) 1

Из формулировки дзеты Эйлера мы можем мгновенно увидеть что дзета ζ(s) не может быть нулём в области с вещественной частью s больше 1, потому что сходящееся бесконечное произведение может быть нулём только если равен нулю один из его множителей. Доказательство бесконечности простых чисел отрицает это.

Формула произведения Эйлера

Существование нулей с вещественной частью 0 ≤ Re(s) ≤ 1

Мы нашли тривиальные нули дзеты в отрицательной полуплоскости, когда Re(s) 1 не может быть нулей.

Однако область между этими двумя областями, называемая критической полосой, была основным центром внимания аналитической теории чисел в течение последних сотен лет.

ДЗЕТА-ФУНКЦИЯ

ДЗЕТА-ФУНКЦИЯ, функция,- 1) Д.-ф. в теории чисел — класс аналитич. функций комплексного переменного, состоящий из ζ-функции Римана, ее обобщений и аналогов. Д.-ф. и их обобщения в виде L-функций (см. Дирихле L-функции) лежат в основе современной аналитич. теории чисел. Кроме ζ-функции Римана выделяются обобщенная Д.-ф. ζ(s, а), дзета-функция Дедекинда, конгруэнц Д.-ф. и др.

Дзета-функция Римана определяется рядом Дирихле

ζ(s) = 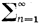1/n s , s = σ +it, (1)

абсолютно и равномерно сходящимся в любой конечной области комплексной s-плоскости, для к-рой σ ≥ 1 + δ, δ > 0. При σ > 1 справедливо представление в виде произведения Эйлера

где р пробегает все простые числа.

Тождественность ряда (1) и произведения (2) представляет собой одно из основных свойств функции ζ(s). Оно позволяет получить многочисленные соотношения, связывающие ξ(s) с важнейшими теоретико-числовыми функциями. Так, при σ > 1

где π(х) — число простых чисел ≤ x, Λ(n) — Мангольдта функция, μ(n) — Мёбиуса функция, τ(n) — число делителей числа n, ν(n) — число простых делителей числа n, λ(n) — Лиувилля функция. Отсюда та исключительная роль, к-рую играет ζ(s) в теории чисел. Как функция действительного переменного, ζ(s) была введена в 1737 Л. Эйлером (L. Euler, см. [1]), к-рый указал и ее разложение в произведение (2). Затем эта функция рассматривалась П. Дирихле (P. Dirichlet) и, особенно успешно, П. Л. Чебышевым (см. [2]) в связи с изучением закона распределения простых чисел. Однако наиболее глубокие свойства функции ζ(s) были обнаружены позднее, когда ее стали рассматривать как функцию комплексного переменного. Первым это сделал в 1876 Б. Риман (В. Riemann, см. [3]), к-рый показал следующее.

а) ζ(s) допускает аналитич. продолжение на всю комплексную s-плоскость в виде

π -s/2 Г(s/2) ζ = 1/(s(s-1)) + 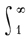(x s/2 — 1 + x (1-s)/2 — 1 )θ(x) dx. (3)

где Г(ω) — гамма-функция,

θ(x) = 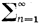ехр(-πn 2 x).

б) ζ(s) является регулярной функцией для всех значений s, кроме s = 1, где она имеет простой полюс с вычетом, равным 1, и удовлетворяет функциональному уравнению

π -s/2 Г(s/2) ζ(s) = π -(1-s)/2 Г((1-s)/2) ζ(1 — s) (4)

Это уравнение наз. функциональным уравнением Римана. Для функции

введенной Б. Риманом для исследования Д.-ф. и называемой кси-функцией Римана, это уравнение принимает вид

а если положить

то оно принимает вид

Последняя функция Ξ замечательна тем, что она является четной целой функцией, действительной для действительных t, и ее нули на действительной оси соответствуют нулям функции ζ(s) на прямой σ = 1/2.

в) Поскольку ζ(s) ≠ 0 для σ > 1, то в силу (4) в полуплоскости σ > 0 эта функция имеет лишь простые нули в точках s = 2ν, ν = 1, 2, . Эти нули наз. тривиальными нулями Д.-ф. ζ(s). Далее ζ(s) ≠ 0 для 0 -2 сходится, а ряд ∑|ρ| -1 расходится.

3. функция ξ(s) представима в виде

P₀(x) = li x — ∑_ρ li x ρ + 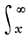du/((u 2 — 1) ln u) — ln 2, (5)

где li x — интегральный логарифм,

5. Все нетривиальные нули Д.-ф. ζ(s) лежат на прямой σ = 1/2.

После Б. Римана проблема значений и, в частности, нулей Д.-ф. приобрела широкую известность и ей посвящено большое число исследований. Гипотезы Римана 2 и 3 были доказаны Ж. Адамаром (J. Hadamard, 1893), причем оказалось, что в гипотезе 3 а = 1/2, b = ln 2 + 1/2 ln &#960 — 1 — C/2. где С — Эйлера постоянная; гипотезы 1 и 4 доказаны X. Мангольдтом (Н. Mangoldt, 1894), к-рый, кроме того, получил, для простых чисел, следующий важный аналог формулы 5. Если

Ψ₀(x) = x — ∑_ρ x ρ /ρ — ζ'(0)/ζ(0) — 1/2 ln (1 — 1/x 2 ),

где ρ = &#946l + iγ пробегает нетривиальные нули ζ(s), а символ ∑_ρ x ρ /ρ означает предел суммы ∑_γ≤T x ρ /ρ при T → -∞. Эта формула, как и формула (5), показывает, что проблема распределения простых чисел в натуральном ряду тесно связана с расположением нетривиальных нулей функции ζ(s).

Последняя гипотеза 5 не доказана и не опровергнута. Это — знаменитая Римана гипотеза о нулях Д.-ф.

Функция ζ(s) однозначно определяется своим функциональным уравнением. Точнее (см. [4]), любая функция, представимая обыкновенным рядом Дирихле и удовлетворяющая уравнению (4), при довольно широких условиях относительно ее регулярности, совпадает с ζ(s) с точностью до постоянного множителя.

и постоянном h > 0 для 0 h, y > h, 2πxy = |t| имеет место приближенное функциональное уравнение

ζ(s) = ∑_n≤x 1/n s + χ(s) ∑_n≤y 1/(n 1-s ) + O(x -σ ) + O(|t| 1/2-σ y σ-1 ), (6)

полученное X. Харди (Н. Hardy) и Дж. Литлвудом (J. Littlewood) в 1920 (см. [4]). Это уравнение играет значительную роль в современной теории Д.-ф. и ее приложениях. Существуют общие методы получения такого рода результатов не только для класса Д.-ф., но и вообще функций Дирихле, обладающих функциональным уравнением риманова типа (3). Наиболее совершенный из них указан в [5]; в случае ζ(s) он приводит, при любом τ с |arg τ| 2 ехр [i(π/2 — 1/|t|) sign t], Δ > 0

получается приближенное уравнение (6); при τ = 1 это соотношение совпадает с исходной формулой (3).

Главной проблемой в теории Д.-ф. является проблема расположения ее нетривиальных нулей и вообще значений в области 1/2 ≤ σ ≤ 1. К числу основных направлений в исследованиях Д.-ф. относятся: определение возможно более широкой области слева от прямой σ = 1, где ζ(s) ≠ 0; проблема порядка и средних значений Д.-ф. в критич. полосе; оценки числа нулей Д.-ф. на прямой σ = 1/2 и вне этой прямой и т. д.

Первый нетривиальный результат о границе нулей Д.-ф. был получен Ш. Ж. Балле Пуссеном (Ch. J. La Vallée-Poussin) в 1896; он показал, что существует такая постоянная А > 0, что

ζ(s) ≠ 0 при σ ≥ 1 — A/(ln α (|t| + 2)) с α ≥ 1. (7)

Дальнейшие продвижения в этом направлении связаны с приближенным уравнением (6) и развитием методов оценок тригонометрич. сумм.

Самый мощный метод оценок такого рода принадлежит И. М. Виноградову (см. Виноградова метод). Последняя (к 1978) граница области, свободной от нулей Д.-ф., получена И. М. Виноградовым в 1958 (см. [7]). Она имеет вид (7) с α > 2/3. Для простых чисел ей соответствует формула

π(х) = li х + O(хе -B ln 3/5 x ).

Существует определенная связь между ростом модуля функции ζ(s) и отсутствием нулей в окрестности прямой σ = 1. Так, результат (7) с α > 2/3 является следствием оценок

ζ(1 + it) = О(ln 2/3 |t|), 1/(ζ(1+it)) = O(ln 2/3 |t|), |t| > 2.

С другой стороны, известно (см. [4]), что

и, если верна гипотеза Римана, то эти пределы, соответственно, не больше, чем 2е C 12/(π 2 e C ).

Порядок дзета-функции в критической полосе есть число η(σ), означающее нижнюю границу таких чисел ν, что ζ(σ + it) = O(|t| ν ).

При σ > 1, ι(σ) = 0, а при σ 1/2.

Это эквивалентно утверждению, что

ζ(1/2 + it) = O(|t| ε ) для любого ε > 0. (8)

При σ > 1/2 справедлива оценка ζ(σ + it) = O(|t| (1-σ)/2 ).

Последняя известная (к 1978) оценка ζ(s) на прямой σ = 1/2 (см. [4]) далека от ожидаемой оценки (8); она имеет вид

ζ(1/2 + it) = O(|t| 15/32+ε ).

Проблема среднего значения дзета-функции состоит в определении свойств функции

1/T 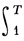|ζ(σ + it)| 2k dt

при Т → ∞ для любого заданного σ и k = 1, 2, . Результаты имеют приложения при изучении проблемы нулей Д.-ф. и непосредственно в теории чисел. Доказано, что (см. [4])

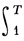
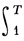
1/T |ζ(1/2 + it)| 2 dt = ln T + 2C — 1 — ln 2π + O(ln T/√T), 1/T |ζ(1/2 + it)| 4 dt = ln 4 T/2π 2 + O(ln 3 T).

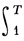
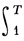
lim_T→∞ 1/T |ζ(σ + it)| 2 dt = |ζ(2σ)|, lim_T→∞ 1/T |ζ(σ + it)| 4 dt = ζ 4 (2σ)/ζ(4σ).

В случаях k > 2 известно только, что при σ > 1 — 1/k

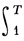
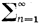
lim_T→∞ 1/T |ζ(σ + it)| 2k dt = τ 2 _k(n)/n 2σ ,

где τ_k(n) — число представлений n в виде k целых положительных сомножителей, и что асимптотич. соотношение

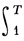
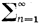
lim_T→∞ 1/T |ζ(σ + it)| 2k dt

τ 2 _k(n)/n 2σ

для σ > 1/2 является эквивалентом гипотезы Линделёфа.

Важное место в теории Д.-ф. занимает проблема оценки функции N(σ, Т), означающей число нулей β + iγ функции ζ(s) при β > σ, 0 s — 1.

Если для нек-рого Х = Х(σ, Т), T 1-l(σ) ≤ X ≤ T A ,

|f_X(s)| 2 dt = O(T l(σ) ln m T)

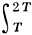
при T → ∞ равномерно для σ ≥ α, где l(σ) — положительная невозрастающая функция с ограниченной производной, а m ≥ 0 — постоянная, то

N(σ, Т) = O(T l(σ) ln m+1 T)

равномерно для σ ≥ α + 1/ln T.

Известно также, что если при r₁ ≤ 3/2

ζ(1/2 + it) = О(t r ln r₁ t),

то равномерно для 1/2 ≤ σ ≤ 1,

N(σ, Т) = O(Т 2(1+2r)(1-σ) ln 5 T)

Эти два предложения позволили получить (см. [4]) следующие плотностные теоремы о нулях дзета-функции:

равномерно для σ ≥ 1/2

N(σ, Т) = O(T 3(1-σ)3;)(2-σ) ln 5 T), N(σ, T) = O(T 1-1/4(σ-1/2) ),

с привлечением иных соображений в [8] получена плотностная теорема:

N(σ, Т) = O(T 5/2(1-σ) ln 13 T);

если справедлива гипотеза Линделёфа, то N(σ, Т) = O(T 2(1-σ)+ε ).

О нулях дзета-функции на прямой σ = 1/2. По гипотезе Римана, все нетривиальные нули Д.-ф. лежат на прямой σ = 1/2. Тот факт, что на этой прямой Д.-ф. имеет бесконечно много нулей, впервые был доказан X. Харди в 1914 (см. [4]) на основе формулы Рамануджана

Последний результат принадлежит А. Сельбергу (A. Selberg, 1942; см. [4]): число N₀(T) нулей ζ(s), имеющих вид 1/2 + it, удовлетворяет неравенству

N₀(T) > AT ln Т, А > 0.

Это означает, что число нулей Д.-ф. на прямой σ = 1/2 имеет тот же порядок роста, что и число всех ее нетривиальных нулей:

Относительно нулей Д.-ф. на этой прямой известны и другого рода результаты. Приближенное функциональное уравнение позволяет фактически вычислить (с нек-рой степенью точности) значения ближайших к действительной оси нулей ζ(s). На основе этого метода на ЭВМ вычислены нули ζ(s) в прямоугольнике 0 ≤ σ ≤ 1, 0 ≤ t ≤ 1,6 ⋅ 10 6 . Их число равно 3,5 ⋅ 10 6 , и все они лежат на прямой σ = 1/2. Ординаты первых шести нулей с точностью до второго десятичного знака равны 14,13; 21,02; 25,01; 30,42; 32,93; 37,58.

Вообще, расстояние между соседними нулями ζ(s) оценивается теоремой Литлвуда (1924): для любого достаточно большого Т функция ζ(s) имеет такой нуль что

При а = 1 она обращается в дзета-функцию Римана. Аналитическое продолжение на всю плоскость осуществляется формулой

где интеграл берется по контуру L, представляющему собой путь из бесконечности по верхнему краю разреза положительной действительной оси до нек-рого фиксированного 0 1, где r₁ — число действительных, r₂ — число пар комплексно сопряженных полей в k; пусть далее Δ — дискриминант, h — число классов дивизоров, R — регулятор поля k, g — число содержащихся в k корней из 1.

Дзета-функция Дедекинда ζ_k(s) поля k определяется рядом

ζ_k = ∑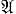 1/N S ,

где пробегает все целые отличные от нуля дивизоры поля k, N — норма дивизора . Этот ряд абсолютно и равномерно сходится при σ ≥ 1 + δ, δ > 0, определяя аналитич. функцию, регулярную в полуплоскости σ > 1.

ζ_k = f(m)/m s ,

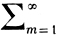
где f(m) — число целых дивизоров поля k с нормой m, f(m) ≤ τ_n(m), τ_n(m) — число представлений т в виде п натуральных сомножителей.

При σ > 1 имеет место тождество Эйлера

где ℬ пробегает все простые дивизоры поля k.

Основные свойства дзета-функции Дедекинда (см. [11]).

1) ζ_k регулярна на всей комплексной плоскости,

кроме точки s = 1, где она имеет простой полюс с вычетом

2) ζ_k удовлетворяет функциональному уравнению

3) При r = r₁ + r₂ — 1 > 0 в точке s = 0 функция ζ_k(s) имеет нуль порядка r; ζ_k(0) ≠ 0 при r = 0; в точках s = -2ν, ν = l, 2, . дзета-функция Дедекинда ζ_k(s) имеет нули порядка r + 1, в точках s = -2ν — 1 при r₂ > 0 — нули порядка r₂, а при r₂ = 0 не равна нулю. Это — тривиальные нули функции ζ_k(s).

4) Все остальные нули функции ζ_k(s) лежат в критич. полосе 0 ≤ σ ≤ 1.

Основная гипотеза состоит в том, что все нетривиальные нули функции ζ_k(s) находятся на прямой σ=1/2. Установлено, что ζ_k(s) не имеет нулей на прямой σ = 1. Более того, существует абсолютная положительная постоянная А и зависящая от параметров поля k постоянная λ, обладающие тем свойством, что

ζ_k(s) ≠ 0 при σ ≥ 1- A/(n ln |t|), |t| > λ.

Вообще, в случае фиксированных параметров поля k для ζ_k(s) имеют место многие результаты, аналогичные результатам для дзета-функции Римана. Однако в общем случае теория дзета-функции Дедекинда сложнее, поскольку она включает в себя и теорию Дирихле L-функций. Так, неизвестно (1978), имеют ли дзета-функции Дедекинда действительные нули между 0 и 1. Точная зависимость между дзета-функцией Дедекинда и L-рядами рационального поля имеет следующий вид. Пусть k * — минимальное поле Галуа, к-рому принадлежит k, Q — группа Галуа поля k * , h — число классов группы Q, χ_i — простые характеры группы Q, 1 ≤ i ≤ h. Тогда

где ζ(s) — дзета-функция Римана, L суть L-ряды Артина, с_i = c_i(k) — целые положительные числа, к-рые определяются свойствами относительной группы Галуа поля k * . В частности, если k — круговое расширение, то k * = k, h = φ(n), c_i = 1, и L-ряды Артина становятся обычными L-рядами Дирихле.

Наряду с дзета-функцией Дедекинда ζ_k(s) рассматриваются и ζ_k(s; H_j) — дзета-функции Дедекинда класса дивизоров H_j поля k. Эти функции определяются теми же рядами, что и ζ_k(s) но только 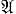пробегает не все, а лишь целые дивизоры, к-рые принадлежат заданному классу H_j. Функции ζ_k(s, H_j) обладают свойствами, близкими свойствам ζ_k(s). Справедлива формула

Дзета-функции Дедекинда лежат в основе современной аналитич. теории дивизоров полей алгебраич. чисел. Здесь они играют такую же роль, какую играет дзета-функция Римана в теории чисел рационального поля.

Аналогом дзета-функции Дедекинда для полей алгебраич. функций от одного переменного с конечным полем констант является конгруэнц дзета-функция, или дзета-функция Артина-Шмидта (см. ниже Дзета-функция в алгебраической геометрии).

Лит.: [1] Эйлер Л., Введение в анализ бесконечно малых, 2 изд., т. 1, пер. с латин., М., 1961; [2] Чебышев П. Л., Избр. математические труды, М.-Л., 1946; [3] Риман Б., Соч., пер. с нем., М.-Л., 1948; [4] Титчмарш Е. К., Теория дзета-функции Римана, пер. с англ., М., 1953; [5] Лаврик А. Ф., «Изв. АН СССР. Сер. матем.», 1968, т. 32, № 1, с. 134-85; [6] Виноградов И. М., Метод тригонометрических сумм в теории чисел, М., 1971; [7] его же, «Изв. АН СССР. Сер. матем.», 1958, т. 22, с. 161-64; [8] Монтгомери X. Л., «Математика», 1970, т. 14, № 5, с. 133-40; [9] Прахар К., Распределение простых чисел, пер. с нем., М., 1967; [10] Чудаков Н. Г., Введение в теорию L-функций Дирихле, М.-Л., 1947; [11] Несkе Е., Mathematische Werke, Gött., 1959.

2) Д.-ф. в алгебраической геометрии — аналитическая функция комплексного переменного s, описывающая арифметику алгебраич. многообразий над конечными полями и схем конечного типа над Spec ℤ. Если X — такая схема, X̅ — множество ее замкнутых точек, a N(x) — число элементов поля вычетов k(х) точки х ∈ Х̅, то Д.-ф. ζ_X(s) задается эйлеровым произведением

Это произведение абсолютно сходится при Re s > dim X, допускает мероморфное продолжение в полуплоскости Re s > dim X — 1/2 и имеет полюс в точке s = dim X (см. [10]). В случае если X = Spec ℤ, то ζ_X(s) есть дзета-функция Римана, а если X конечна над Spec ℤ, то ζ_X(s) есть дзета-функция Дедекинда числового поля.

Наиболее изучена ситуация, когда X является алгебраич. многообразием, определенным над конечным полем F_q. В этом случае

где deg х — степень поля k(х) над полем F_q и вместо функции ζ_X(s) обычно рассматривают функцию Z_X(t) такую, что

Если ν_n — число рациональных точек многообразия X в поле F_{q n} , то оказывается (см. [14]), что

ln Z_X(t) = 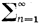ν_n t_n/n.

Такие Д.-ф. были введены впервые для случая алгебраич. кривых (по аналогии с полями алгебраич. чисел) в 1924 Э. Артином [1], к-рый заметил, что они являются рациональными функциями от t и для них в нек-рых случаях верен аналог гипотезы Римана о нулях. Этот аналог получил название гипотезы Артина. Для кривых рода 1 она была доказана X. Хассе (Н. Hasse) в 1933 (в случае рода 0 ситуация тривиальна), а для кривых произвольного рода — А. Вейлем (A. Weil) в 1940 при помощи результатов теории абелевых многообразий, созданной им в значительной мере для этой цели (см. [2], [14]).

А. Вейль [2] рассмотрел Д.-ф. произвольных алгебраич. многообразий и высказал гипотезы, обобщающие результаты, полученные к тому времени для кривых. Его исследования основаны на следующем замечании — множество точек многообразия X, рациональных над F_{q a} , является множеством неподвижных точек а-й степени Фробениуса эндоморфизма этого многообразия. Первая гипотеза Вейля состоит в том, что в категории алгебраич. многообразий над конечными полями существует теория когомологий, удовлетворяющая всем формальным свойствам, необходимым для получения Лефшеца формулы. Если <Н i (Х)>— группы когомологий такой теории, то из формулы Лефшеца следует, что

где n = dim X, а P_i(t) — характеристич. многочлены отображений, индуцированных эндоморфизмом Фробениуса на Вейля когомологиях Н i (Х). В частности, функция ζ_X(t) рациональна.

Вторая гипотеза Вейля состоит в том, что функция ζ_X(t) должна удовлетворять функциональному уравнению, имеющему в случае гладкого проективного многообразия X вид

ζ_X(q -n t -1 ) = (-1) χ q nχ/2 t χ ζ_X(t),

где χ — эйлерова характеристика, равная ∑(-1) l dim Н i (Х). (Эта гипотеза является формальным следствием существования теории когомологий.) Рациональность ζ-функции для любых X доказана Б. Двор-ком [6] методом, не использующим когомологии. Теория когомологий, предсказанная А. Вейлем, была создана А. Гротендиком (A. Grothendieck) в 1958 (см. Вейля когомологии, Топологизированная категория, l-адические когомологии). А. Гротендик вместе с М. Артином (М. Artin) доказал обе гипотезы Вейля для гладких проективных многообразий, причем многочлены P_j(t) имели, вообще говоря, целые l-адические коэффициенты, зависящие от выбора простого l, положенного в основу теории. Предполагается, что на самом деле коэффициенты являются целыми числами, не зависящими от l и вообще от выбора теории когомологий. Это высказывание обычно наз. третьей гипотезой Вейля. Наконец, последняя — четвертая гипотеза Вейля относится к нулям α_i многочленов Р_i(t), рассматриваемым как целые алгебраич. числа (гипотеза Римана):

Все эти гипотезы доказаны П. Делинем [4].

Основные применения гипотез Вейля в теории чисел относятся к изучению сравнений. Уже в случае кривых из теоремы Вейля вытекала наилучшая оценка для рациональной тригонометрич. суммы от одной переменной (см. [14]). Эти оценки были обобщены на суммы от любого числа переменных. Другим важным приложением этой теории являются оценки коэффициентов Фурье модулярных форм (проблема Рамануджана-Петерсона, см. [4], [15]).

Приведенные результаты являются на самом деле частными случаями гораздо более общих теорем, относящихся к произвольным L-функциям, к-рые связаны с представлениями групп Галуа накрытий многообразия X или, более общо, с нек-рым l-адическим пучком на X (см. [5], [10]). Эти функции служат на произвольных схемах аналогом известных в теории алгебраич. чисел L-функций.

Пусть теперь X — схема конечного типа над Spec Z такая, что ее общий слой X ⊗_X Q является непустым алгебраич. многообразием над полем рациональных чисел Q. Существует предположение, что Д.-ф. ζ_X(s) имеют мероморфные продолжения на всю s-плоскость и удовлетворяют функциональному уравнению. Гипотетич. вид этого уравнения предложен в [11]. Доказать эту гипотезу удалось пока (1978) лишь в очень специальных случаях (рациональные поверхности, алгебраич. кривые, униформизуемые модулярными функциями, абелевы многообразия с комплексным умножением, см. [15]). Что касается аналога гипотезы Римана, то он в этой ситуации даже не сформулирован.

Новый круг идей в изучении Д.-ф. принесли работы Дж. Берча (J. Birch), П. Суиннертон-Дайера [12] и Дж. Тейта [13]. Чтобы сформулировать принадлежащие им гипотезы, следует заметить, что функция ζ_Xp(s) является произведением Д.-ф. ζ_Xp(s) слоев Х_p отображения X → Spec ℤ. Для последних, являющихся многообразиями над конечными полями, имеется, согласно первой гипотезе Вейля, разложение на многочлены. После перемножения этих разложений получается аналогичное представление для Д.-ф.

Гипотеза Берча и Суиннертон-Дайера предполагает, что порядок нуля функции ζ (i) _X(s) в точке s = dim X — 1 равен рангу группы рациональных точек многообразия Пикара Pic X (конечному, в силу теоремы Морделла — Вейля). Эта гипотеза, тем самым, предполагает справедливость гипотезы о мероморфном продолжении Д.-ф.

В первоначальной форме гипотеза Берча и Суиннертон-Дайера была высказана для эллиптич. кривых над полем Q в результате изучения обширных таблиц для кривых с комплексным умножением [12]. В дальнейшем было высказано предположение о значении коэффициента при соответствующей степени переменной s в разложении функции ζ (1) _X(s) в окрестности точки s = dim X — 1. Предполагается, что он равен

где [II] — предполагаемый конечным порядок группы Шафаревича — Тейта локально тривиальных главных однородных пространств многообразия Pic X, |det(a’_i, a_j)| — определитель билинейной формы на группе рациональных точек многообразия Pic X, получающийся из высоты точки, [Pic X_tors] и [Pic’ X_tors] — порядки подгрупп кручения в группе рациональных точек на Pic X и двойственном абелевом многообразии. Это выражение обобщает хорошо известное в теории алгебраич. чисел выражение для вычета дзета-функции Дедекинда в точке s = 1. Одной из трудностей на пути к доказательству гипотезы Берча и Суиннертон-Дайера является тот факт, что группа III полностью не вычислена (1978) ни для одной кривой. Доказан аналог этой гипотезы для кривых, определенных над полем функций, однако и в этом случае пришлось предположить конечность Брауэра группы, играющей здесь роль группы III (см. [5]).

Дж. Тейт [13], изучая действие группы Галуа на алгебраич. циклы многообразий, выдвинул гипотезы о полюсах функций ζ (i) _X(s) при четных значениях i, а именно,

что функция ζ (2i) _X(s) имеет в точке s = i + 1 полюс порядка, равного рангу группы алгебраич. циклов коразмерности i. Это утверждение тесно связано с гипотезой Тейта об алгебраич. циклах. По поводу имеющихся подходов к доказательству этих гипотез, а также различных аргументов в их пользу см. [5], [7], [12], [13], [17].

Независимо от описываемого здесь понятия Д.-ф. в теории алгебраич. групп и автоморфных функций возникли и изучались Д.-ф., являющиеся преобразованиями Меллина модулярных форм. В 1967 А. Вейль заметил, что из общих гипотез о функции ζ (1) _X(s) для эллиптич. кривой X над Q вытекает, что кривая X униформизуется модулярными функциями, а функция ζ (1) _X(s) есть. преобразование Меллина модулярной формы, отвечающей дифференциалу рода 1 на X. Это замечание привело-к предположению о том, что функции ζ (i) _X(s) любой схемы X являются преобразованиями Меллина подходящих модулярных форм. Основные результаты в этом направлении были получены Э. Жаке и Р. Ленглендсом (см. [7], [9]). В частности, они построили широкий класс рядов Дирихле, удовлетворяющих нек-рому функциональному уравнению и разлагающихся в эйлерово произведение, к-рые можно представить в виде преобразования Меллина модулярных форм на группе GL(2). Выполнимость условий их теоремы непосредственно связана с приведенными выше гипотезами об общих свойствах Д.-ф. Пока их удается проверить лишь для кривых, определенных над полем функций.

Начиная с 1970 под влиянием работ о p-адических Д.-ф. полей алгебраич. чисел (см. [14]) возникает аналогичный подход и к Д.-ф. схем, главным образом эллиптич. кривых. Имеющиеся здесь проблемы, во многом похожие на рассмотренные выше, отражены в [9]. Д.-ф. эллиптич. кривой над Q тесно связана с одномерной формальной группой кривой и они полностью друг друга определяют [16].

Лит.: [1] Аrtin Е., «Math. Z.», 1924, Bd 19, S. 153-246; [2] Weil A., Surles courbes algebriques et les varietes quis’en deduisent, P., 1948; [3] eго жe, «Bull. Amer. Math. Soc.». 1949, v. 55, № 5, p. 497 -508; [4] Deligne P., «Publ. Math. IHES», 1974, t. 43, p. 273-307; [5] Dix exposès sur la cohomologie des schémas, Amst.-P., 1968; [6] Dwоrk В., в кн.: Proceedings of the International Congress of Mathematicians. Djursholm, 1963, p. 247 — 59; [7] Жаке Э., Ленгленде P., Автоморфные формы на GL(2), пер. с англ., М., 1973; [8] Манин Ю. И., «Успехи матем. наук», 1971, т. 26, в. 6, с. 7-71; [9] Modular functions of one variable, В., 1973; [10] Сepp Ж.-П., «Успехи матем. наук», 1965, т. 20, № 6, с. 19-26; [11] его же, «Математика», 1971, т. 15, № 1, с. 3-13; [12] Свиннертон-Дайер П., «Математика», 1969, т. 13, № 5, с. 3-25; [13] Тэйт Д., «Успехи матем. наук», 1965, т.20, № 6, с. 27-40; [14] Шафаревич И. Р., Дзета-функция, М., 1969; [15] Шимура Г., Введение в арифметическую теорию автоморфных функций, пер. с англ., М., 1973; [16] Xонда Т., «Математика», 1969, т. 13, № 6, с. 3-17; [17] Итоги науки. Алгебра. Топология. Геометрия. 1970, М., 1971, с. 111-51.

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д — Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.