Функциональные уравнения задающие элементарные функции

Функциональные уравнения. Методы их решения

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Министерство образования и молодежной политики Чувашской Республики

БОУ ДПО (ПК) С «Чувашский республиканский институт образования»

Кафедра математики и информационных технологий

Курсовая работа на тему:

« Функциональные уравнения. Методы их решения»

Выполнил (а): учитель математики МБОУ «СОШ № 60»

Глава 1. Понятие функционального уравнения ………………………………. 5

Глава 2. Практическая часть. Методы решения функционального уравнения.9

Одно из важнейших математических умений, которым должны овладеть учащиеся школы, — умение решать уравнения. Корень уравнения находят в одно или более действий, многие текстовые задачи решаются алгебраическим способом, в уравнении могут участвовать целые, рациональные и другие числа, то есть уравнения одновременно сами по себе являются задачами и способами решения задач, умение, решать, которые необходимы всем учащимся школы. Но во время решения тренировочных заданий мне попалось уравнение, которое я решить не смогла. Как я узнала позже от учителя, это было функциональное уравнение.

Что же такое функциональные уравнения? И какие способы их решения существуют? Эти вопросы заинтересовали меня, и я решила провести исследование. функциональный уравнение коши

Функциональными уравнениями занимаются с очень давних пор, этому курсу так и не нашлось достойного места в математических программах. А жаль. Ведь решение отдельных функциональных уравнений требует достаточно глубокого понимания предмета и прививает любовь к самостоятельной творческой работе. Так как эта тема в школьном курсе не изучается в виду её сложности, при поступлении в престижные ВУЗы, на олимпиадах, в части С ЕГЭ такие задачи встречаются.

В настоящее время практически нет никаких пособий, обучающих решению функциональных уравнений.

Поэтому ощущается потребность в пособии, которое на простых и конкретных примерах способно показать читателю со скромной математической подготовкой весь арсенал современных методов решения функциональных уравнений.

Цель работы — выяснить, что является функциональным уравнением их системами, найти способы решения и составить сборник задач для использования математическими классами.

1. изучение и анализ литературы;

2. поиск способов решения функциональных уравнений и их систем;

3. решение функциональных уравнений

4. составление сборника

Объект исследования: функциональные уравнения

Предмет исследования: изучение свойств и способов решения функциональных уравнений.

Структура: введение, понятие функционального уравнения, сборник задач, заключение.

Глава 1. Понятие функционального уравнения

Функциональное уравнение – это уравнение, которое содержит одну или несколько неизвестных функций (с заданными областями определения и значений). Решить функциональное уравнение – это, значит, найти все функции, которые тождественно ему удовлетворяют. Функциональные уравнения возникают в самых различных областях математики, обычно в тех случаях, когда требуется описать все функции, обладающие заданными свойствами. Термин функциональное уравнение обычно используется для уравнений, несводимых простыми способами к алгебраическим уравнениям. Эта несводимость чаще всего обусловлена тем, что аргументами неизвестной функции в уравнении являются не сами независимые переменные, а некоторые данные функции от них. Часто встречаются на различных математических соревнованиях.

Некоторые функциональные уравнения знакомы нам еще из школьного курса это

которые задают такие свойства функций, как чётность, нечётность, периодичность.

Задача решения функциональных уравнений является одной из самых старых в математическом анализе. Они появились почти одновременно с зачатками теории функций. Первый настоящий расцвет этой дисциплины связан с проблемой параллелограмма сил. Ещё в 1769 году Даламбер свёл обоснование закона сложения сил к решению функционального уравнения

(1)

То же уравнение и с той же целью было рассмотрено Пуассоном в 1804 году при некотором предположении аналитичности, между тем как в 1821 году Коши (1789 – 1857) нашёл общие решения

этого уравнения, предполагая только непрерывность f(x).

Даже известная формула неевклидовой геометрии для угла параллельности

была получена Н. И. Лобачевским (1792 – 1856) из функционального уравнения

, (2)

которое он решил методом, аналогичным методу Коши. Это уравнение можно привести к уравнению

.

Ряд геометрических задач, приводящих к функциональным уравнениям, рассматривал английский математик Ч. Баббедж (1792—1871). Он изучал, например, периодические кривые второго порядка, определяемые следующим свойством для любой пары точек кривой: если абсцисса второй точки равна ординате первой, то ордината второй точки равна абсциссе первой. Пусть такая кривая является графиком функции у = f(х) ; (х, f(х)) — произвольная ее точка. Тогда, согласно условию, точка с абсциссой f(х) имеет ординату х. Следовательно,

(3)

Функциональному уравнению (3) удовлетворяют, в частности, функции:

,

Одними из простейших функциональных уравнений являются уравнения Коши

Эти уравнения Коши подробно изучил в своём (Курсе Анализа), изданном в 1821 году. Непрерывные решения этих четырёх основных уравнений имеют соответственно вид

, , ,

В классе разрывных функций могут быть и другие решения. Уравнение (4) ранее рассматривалось Лежандром и Гауссом при выводе основной теоремы проективной геометрии и при исследовании гауссовского закона распределения вероятностей.

Функциональное уравнение (4) было опять применено Г. Дарбу к проблеме параллелограмма сил и к основной теореме проективной геометрии; его главное достижение — значительное ослабление предположений. Мы знаем, что функциональное уравнение Коши (4) характеризует в классе непрерывных функций линейную однородную функцию f(x) = ax . Дарбу же показал, что всякое решение, непрерывное хотя бы в одной точке или же ограниченное сверху (или снизу) в произвольно малом интервале, также должно иметь вид f(x) = ax. Дальнейшие результаты по ослаблению предположений следовали быстро один за другим (интегрируемость, измеримость на множестве положительной меры и даже мажорируемость измеримой функцией). Возникает вопрос: существует ли хоть одна какая-нибудь аддитивная функция (т. е. удовлетворяющая (4)), отличная от линейной однородной. Найти такую функцию действительно нелегко! В ходе работы мы покажем, что при рациональных x значения любой аддитивной функции должны совпадать со значениями некоторой линейной однородной функции, т. е. f(x) = ax для x Q. Казалось бы, что тогда f(x) = ax для всех действительных x. Если f(x) — непрерывна, то это действительно так, если же данное предположение отбросить — то нет. Первый пример отличного от f(x) = ax разрывного решения функционального уравнения (4) построил в 1905 году немецкий математик Г. Гамель с помощью введённого им базиса действительных чисел.

Многие функциональные уравнения не определяют конкретную функцию, а задают широкий класс функций, т. е. выражают свойство, характеризующее тот или иной класс функций. Например, функциональное уравнение f(x+1) = f(x) характеризует класс функций, имеющих период 1, а уравнение f(1+x) = f(1-x) — класс функций, симметричных относительно прямой x = 1 , и т. д.

Элементарное введение в функциональные уравнения

Теория и примеры решения функциональных уравнений

Просмотр содержимого документа
«Элементарное введение в функциональные уравнения»

1.Функциональные уравнения. Их свойства и методы решения. 5

1.1 Определение и примеры функциональных уравнений. 5

1.2 Методы решения функциональных уравнений. 8

2. Решение функциональных уравнений Коши на множестве Q рациональных чисел. 13

2.1 Решение уравнения вида f(x+y)=f(x)+f(y) на Q. 13

2.2 Решение уравнения вида f(x+y)=f(x)∙f(y) на Q. 15

2.3 Решение уравнения вида f(x∙y)=f(x)+f(y) на Q. 17

2.4 Решение уравнения вида f(x∙y)=f(x)∙f(y) на Q. 19

3. Решение функциональных уравнений Коши на R. 22

3.1 Решение уравнения вида f(x+y)=f(x)+f(y) на оси R. 22

3.2 Решение уравнения вида f(x+y)=f(x)∙f(y) на оси R. 23

4. Решение функциональных уравнений Коши в измеримых функциях. 25

5. Класс уравнений типа Коши. 27

Список использованных источников. 30

Курсовая работа посвящена изучению функциональных уравнений, весьма общему классу уравнений, в которых искомой является некоторая функция.

К функциональным уравнениям по существу относятся дифференциальные уравнения, интегральные уравнения, уравнения в конечных разностях; следует, однако, отметить, что название функциональные уравнения обычно не относят к уравнениям этих типов. Под функциональными уравнениями в узком смысле слова понимают уравнения, в которых искомые функции связаны с известными функциями одного или нескольких переменных при помощи операции образования сложной функции. Функциональные уравнения можно также рассматривать как выражение свойства, характеризующего тот или иной класс функций.

Функциональное уравнение — это уравнение, в котором неизвестными являются функции (одна или несколько). Например,

Некоторые функциональные уравнения знакомы нам еще из школьного курса это f(x) = f(-x), f(-x) = — f(x), f(x+T) = f(x), которые задают такие свойства функций, как чётность, нечётность, периодичность.

Задача решения функциональных уравнений является одной из самых старых в математическом анализе. Они появились почти одновременно с зачатками теории функций. Первый настоящий расцвет этой дисциплины связан с проблемой параллелограмма сил. Ещё в 1769 году Даламбер свёл обоснование закона сложения сил к решению функционального уравнения

(1)

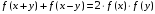
То же уравнение и с той же целью было рассмотрено Пуассоном в 1804 году при некотором предположении аналитичности, между тем как в 1821 году Коши (1789 – 1857) нашёл общие решения

Ряд геометрических задач, приводящих к функциональным уравнениям, рассматривал английский математик Ч. Баббедж (1792—1871). Он изучал, например, периодические кривые второго порядка, определяемые следующим свойством для любой пары точек кривой: если абсцисса второй точки равна ординате первой, то ордината второй точки равна абсциссе первой. Пусть такая кривая является графиком функции у = f(х); (х, f(х)) — произвольная ее точка. Тогда, согласно условию, точка с абсциссой f(х) имеет ординату х. Следовательно,

(2)

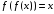
Функциональному уравнению (2) удовлетворяют, в частности, функции: ,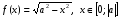

1. Функциональные уравнения. Их свойства и методы решения

1.1 Определение и примеры функциональных уравнений

Функциональные уравнения — весьма общий класс уравнений, в которых искомой является некоторая функция. К функциональным уравнениям, по существу, относятся дифференциальные уравнения, интегральные уравнения, уравнения в конечных разностях. Следует, однако, отметить, что название «функциональные уравнения» обычно не относят к уравнениям этих типов. Под функциональными уравнениями в узком смысле слова понимают уравнения, в которых искомые функции связаны с известными функциями одного или нескольких переменных при помощи операции образования сложной функции. Функциональные уравнения можно также рассматривать как выражение свойства, характеризующего тот или иной класс функций.

Например, функциональное уравнение f (x) = f (-x) характеризует класс чётных функций, функциональное уравнение f(-x) = -f(x) – класс нечетных; функциональное уравнение f (x + 1) = f (x) — класс функций, имеющих период 1, и т.д.

Одним из простейших функциональных уравнений является уравнение

f (x + у) = f (x) + f (y).

Непрерывные решения этого функционального уравнения имеют вид:

Однако в классе разрывных функций это функциональное уравнение имеет и иные решения. С рассмотренным функциональным уравнением связаны

f (x + у) = f (x) f (y),

непрерывные решения которых имеют соответственно вид e Cx , C∙lnx, x a (x 0).

Т.о., эти функциональные уравнения могут служить для определения показательной, логарифмической и степенной функций. В теории аналитических функций функциональные уравнения часто применяются для введения новых классов функций.

Например, двоякопериодические функции характеризуются функциональными уравнениями:

f (z + а) = f (z) и f (z + b) = f (z),

автоморфные функции — функциональными уравнениями:

где a> — некоторая группа дробно-линейных преобразований.

Если функция известна в некоторой области, то знание для неё функционального уравнения позволяет расширить область определения этой функции. Например, функциональное уравнение f (x + 1) = f (x) для периодических функций позволяет определить их значение в любой точке по значениям на отрезке [0, 1]. Этим часто пользуются для аналитического продолжения функций комплексного переменного. Например, пользуясь функциональным уравнением Г (z + 1) = z∙Г (z) и зная значения гамма-функции Г(z) в полосе 0 Re z

Условия симметрии, имеющиеся в какой-либо физической задаче, обусловливают определённые законы преобразования решений этой задачи при тех или иных преобразованиях координат. Этим определяются функциональные уравнения, которым должно удовлетворять решение данной задачи. Значение соответствующих функциональных уравнений во многих случаях облегчает нахождение решений.

Решения функциональных уравнений могут быть как конкретными функциями, так и классами функций, зависящими от произвольных параметров или произвольных функций.

Для некоторых функциональных уравнений общее решение может быть найдено, если известны одно или несколько его частных решений. Например, общее решение функционального уравнения

где j(x) — произвольная функция, а w(x) — частное решение этого функционального уравнения

Для решения функциональных уравнений их во многих случаях сводят к дифференциальным уравнениям. Этот метод даёт лишь решения, принадлежащие классу дифференцируемых функций.

Другим методом решения функциональных уравнений является метод итераций. Этот метод даёт, например, решение уравнения Абеля:

где a(x) — заданная функция и связанного с ним уравнения Шрёдера:

А. Н. Коркин доказал, что если a(х) — аналитическая функция, то уравнение Абеля имеет аналитическое решение. Эти результаты, нашедшие применение в теории групп Ли, привели в дальнейшем к созданию теории итераций аналитических функций. В некоторых случаях уравнение Абеля решается в конечном виде [1].

Функциональные уравнения: Часть 1

Эта трилогия статьей будет посвящена функциональным уравнениям. В данной статье попытаемся понять что такое функциональное уравнение и с чем его едят. В следующих статьях рассмотрим конкретные методы решения более сложных функциональных уравнений(метод подстановок, и подобное).

Функциональное уравнение — уравнение, связующее значение функции в одной точке с её значениями в других точках.

Другими словами, в функциональных уравнениях место неизвестного занимает функция. Для примера, рассмотрим такое функциональное уравнение:
$$display$$2f(x)=2$$display$$ Тут интуитивно хочется разделить обе части уравнения на 2, что сработает и мы узнаем ответ: $$display$$2f(x)=2 \Rightarrow f(x)=1$$display$$ Значит ответом на функциональное уравнение может быть только значение f(x), или похожее (это обычно указывают в условии задачи).
Рассмотрим некое функциональное уравнение, где с обоих сторон будут стоят функции. $$display$$4f(x)=2f(x)+2x \Rightarrow 2f(x)=f(x)+x \Rightarrow f(x)=x$$display$$ Стоит отметить что функция всегда имеет под собой число ($inline$f(x)=x+2, f(1)=3, f(5)=7$inline$, а значит можно производить над ними арифметические операции. Давайте рассмотрим функциональное уравнение из двумя переменными. Задание : найти все функции $inline$f: \mathbb \rightarrow \mathbb$inline$ для каких $inline$4f(x+y)=f(x)+f(y)+2$inline$. В случаях из двумя переменными необходимо припустить что $inline$x=y=0$inline$, из этого мы узнаем значение $inline$f(0)$inline$.

$inline$x=y=0$inline$
$inline$4f(0)=2f(0)+2$inline$
$inline$2f(0)=2 \Rightarrow f(0)=1$inline$

Узнав значение $inline$f(0)$inline$, приравниваем $inline$y$inline$ к нулю. Таким образом узнаем значение $inline$f(x)$inline$

$inline$y=0$inline$
$inline$4f(x)=f(x)+f(0)+2$inline$
$inline$3f(x) = 3 \Rightarrow f($inline$f(x)=kx$inline$x)=1 $inline$
Ответ: $inline$ f(x)=1 $inline$

При такого вида уравнениях обязательно необходимо предполагать что $inline$x=y=0$inline$, но не всегда $inline$x=0\vee y=0$inline$. Существуют такие аналоги как: $inline$x=y, x=f(y), . $inline$. К примеру, $inline$4f(x-y)=f(x)+f(y)+2$inline$. Подставляем $inline$x=y=0$inline$, получаем $inline$4f(0)=2f(0)+2 \Rightarrow f(0)=1$inline$, тогда $inline$x=y$inline$ значит $inline$4f(0)=2f(x)+2$inline$, разделим обе части уравнения на 2 получим что $inline$2f(0)=f(x)+1 \Rightarrow f(x)=1+2f(0) \Rightarrow f(x)=3$inline$, произведем проверку, которая показывает что $inline$f(x)=3$inline$ есть решением данного функционального уравнения.
Теорема 1. Функциональное уравнение Коши $inline$f(x+y)=f(x)+f(y)$inline$ удовлетворяют все линейные функции вида $inline$f(x)=kx$inline$ (1)
Теорема 2. Функциональное уравнение $inline$f(x+y)=f(x)f(y)$inline$ удовлетворяют все показательные функции вида $inline$f(x)=k^$inline$ (2)
Теорема 3. Функциональное уравнение $inline$f(xy)=f(x)+f(y)$inline$ удовлетворяют все логарифмические функции вида $inline$f(x)=log_k (x)$inline$ (3)
Теорема 4. Функциональное уравнение $inline$f(xy)=f(x)f(y)$inline$ удовлетворяют все степенные функции вида $inline$f(x)=x^$inline$ (4)
Доведем их.
$$display$$(1) f(x+y)=a(x+y), f(x)+f(y) = ax+ay \Rightarrow f(x+y)=f(x)+f(y)$$display$$
$$display$$(2) f(x+y)=a^, f(x)f(y) = a^a^ \Rightarrow f(x+y)=f(x)f(y)$$display$$
$$display$$(3) f(xy)=log_a (xy), f(x)+f(y)=log_a(x)+log_a(y) \Rightarrow f(xy)=f(x)+f(y)$$display$$
$$display$$(4) f(xy)=(xy)^, f(x)f(y) = x^y^ \Rightarrow f(xy)=f(x)f(y)$$display$$
Теорема 5. Уравнения Йенсена $inline$f(\frac<2>)=\frac<2>, f(x)=kx+b$inline$, доводиться аналогично предыдущим.

Рассмотрим такую задачу: Найдите все линейные функции вида $inline$f(x)=ax, $inline$$inline$f: \mathbb \rightarrow \mathbb$inline$ для которых правильно $inline$4(f(x-y)+f(x+y)+1)=2f(x)+f(y-1)$inline$.

Воспользуемся теоремой 1.
$inline$4(f(x-y)+f(x+y)+1) = 4(f(x)-f(y)+f(x)-f(y)+1) = 4$inline$
$inline$4=2f(x)+f(y-1)$inline$
Тут ключевой момент. Нельзя подставлять $inline$x=y=0$inline$, так как ничего не получиться. Необходимо подставить $inline$x=0, y=x+1$inline$, тогда мы сможем узнать $inline$f(0)$inline$.
$$display$$4=2f(0)+f(0) \Rightarrow 4=3f(0) \Rightarrow f(0)=\frac<4><3>$$display$$. Тогда подставляем $inline$x=y-1$inline$, и получаем $inline$4=2f(x)+f(x) \Rightarrow 4=3f(x) \Rightarrow f(x)=\frac<4><3>$inline$
Ответ: $inline$f(x)=\frac<4><3>$inline$