Функция гамильтона и канонические уравнения

ГА́МИЛЬТОНА УРАВНЕ́НИЯ

ГА́МИЛЬТОНА УРАВНЕ́НИЯ (ка­но­ни­че­ские урав­не­ния ме­ха­ни­ки), диф­фе­рен­ци­аль­ные урав­не­ния дви­же­ния го­ло­ном­ных ме­ха­нич. сис­тем, на­хо­дя­щих­ся под дей­ст­ви­ем по­тен­ци­аль­ных сил. Пред­ло­же­ны У. Га­миль­то­ном в 1834.

Канонические уравнения Гамильтона и формулы

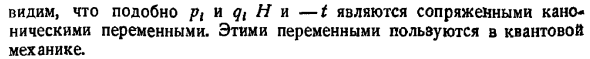
Канонические уравнения Гамильтона

• Подумайте о консервативной материальной системе, где свобода — это s. Обобщенные координаты qb qt, qs select. Чтобы использовать эту систему, используя уравнение Лагранжа 2-го порядка, необходимо создать дифференциальное уравнение 2-го порядка. Для П-функции Лагранжа. Уменьшите число уравнений в 2 раза, чтобы уменьшить порядок первого дифференциального уравнения из 2-го дифференциального уравнения.

Создание нормального уравнения рекомендуется выполнять в следующем порядке. 1 Найти число степеней свободы данной консервативной материальной системы и выбрать соответствующие обобщенные координаты 2 Найти обобщенный импульс, сопряженный с выбранными обобщенными координатами см. пункт 1 в этом разделе 3 вычислить функцию Гамильтона см. подраздел 2 в этом разделе.4 Создайте стандартное уравнение, используя формулу 8.Задание 17.12.Создайте стандартное уравнение движения свободных материальных точек массой m в гравитационном поле. Выберите декартовы координаты x, y и r в качестве обобщенных координат. Решение.

Вторые слагаемые уравнений (9) и (20) соответственно определяют вынужденные колебания стрелки В при отсутствии и при наличии силы сопротивления движению. Людмила Фирмаль

Это можно сделать по-разному ways .In в частности, если к координатам добавляются дополнительные координаты-универсальный момент pt, pp. Параметры qt и 1 2.. A называется регулярной переменной. Обобщенная координата qt и соответствующий ей импульс p сопряженная называется канонической переменной. Эти 2 канонические переменные соответствуют 2 из канонического уравнения Гамильтона. Где i-функция Гамильтона, 4 1, 2,. .это Каноническое уравнение Гамильтона является обыкновенным дифференциальным уравнением на 2-м этаже а не частным дифференциалом это не. Помимо механики, стандартные уравнения используются в квантовой механике, электродинамике и других дисциплинах теоретической физики.

Есть 3 степени свободы для свободного материала points .So, чтобы объяснить его движение, нам нужно 6 канонических переменных. Обобщенный импульс px, pu, pg был задан в уравнении вещества 17.7 2.Создайте 6 уравнений Гамильтона 8.в этом случае у вас есть следующий вид пеленгатор 5G ОТЛИЧИТЕЛЬНОЕ ИМЯ. ГПЦ прочая Л. Используйте функцию Гамильтона H, составленную в вопросе 17.9 см. уравнение 3 W 2 pl p pl wgz .Подставляя это значение и в уравнение 1, находим искомое стандартное уравнение.— П.

Эти канонические уравнения размером 1 на 6 для переменных x, y, z, px, Py, pg можно свести к дифференциальным уравнениям размером 2 на 3 для переменных x, y и R. In факт, вычисляя производные по Времени первых 3 канонических уравнений 2 и решая их относительно px, pu, px Подставляя уравнение 2 Эти значения находятся в последних 3 стандартных px, pu, pg после уменьшения m .e 0, J 0 2 г. 3. Уравнение 3 является дифференциальным уравнением для свободных материальных точек в гравитационном поле проекции на Декартовы координатные оси.

Задача 17.13. To создайте стандартное уравнение движения свободной материальной точки массой m под действием квазиупругой силы F cr см. Рисунок, c-постоянный коэффициент. Игнорируйте сопротивление движению. Выберите декартовы координаты x, y и g в качестве обобщенных координат. Решение. Есть 3 степени свободы для свободных материальных точек.3 обобщенные координаты Oi x, Q z К выпуску 17.13.Существует 3 сопряженных обобщенных импульса px, pu, pg .вычислить кинетическую энергию массы точек для определения ПВ, Пу, И П Т 4-1Н м х 2 Л- 1 Обобщенный импульс равен Сила F-это потенциал, и поскольку связи нет, функция Гамильтона равна его полной механической энергии.

Напомним, что потенциальная энергия-это работа, которую потенциальная сила выполняет при перемещении материальной точки из определенного положения в другое. zero .So в этом случае О, да.— ЗР -Р-РФР — в.4 заметим, что r2×2 y z2, запишем Формулу 4 в следующем формате н х ЮЖД з.5 Если подставить результат I и b выражения 3 Уравнение 6 все еще должно зависеть от обобщенных координат и обобщения, поэтому функция Гамильтона пока не нужна. Шейка матки impulse .So, используя формулу 2, мы представляем обобщенную скорость в соответствии с обобщенным импульсом.

• Введем выражения A, и получим Гамильтонову функцию в выражении 6 в виде Приступим к созданию канонического уравнения ду Р 7. Формат в этом случае является Подставим формулу функции в формулу 8 и получим стандартное уравнение интересующего движения из Формулы 7.Т ПРОМАЛЬП — СХ ру — П — автомат. 9 6 канонических переменных х, г, р, РХ, Р Мы получили 1 6-е каноническое уравнение, соответствующее П. эти уравнения можно свести к 2, 3 дифференциальным уравнениям в проекции на Декартовы оси. Для этого нужно дифференцировать первые 3 канонических уравнения 9, решить их относительно px, pu, p и подставить найденные pn, p в последние 3 уравнения 9.Возьми н — СХ, ту — КР, м3 — автомат.

Уравнение 10 является проекцией векторного уравнения mw F, то есть mw — cg на Декартовы координатные оси. Задание 17.14, составьте стандартное уравнение движения свободных материальных точек массой m под действием центральной силы. Энергия положения равна P P g .Выбираем полярные координаты р и Р, так как они являются обобщенными. Решение.2 обобщенные координаты r и p соответствуют 2 сопряженным импульсам pg и pf .Они были рассчитаны в решении задачи 17.7 см. уравнение 5.Центральная сила F-это потенциал, и нет никакой связи, поэтому функция Гамильтона равна сумме механической энергии.

При наличии силы сопротивления движению, пропорциональной скорости ползуна, колебания с частотой свободных колебаний затухают и стрелка прибора регистрирует. Людмила Фирмаль

Используя уравнение кинетической энергии задачи 17.7 4, запишем Гг, Р, 1 р р.2 Здесь в функции надо необходимо выразить обобщенный импульс PN P и обобщенные скорости T и относительно координат R, P .используя формулу в вопросе 17.7 5 И затем Канонические уравнения В этом деле Получим искомое стандартное уравнение для движения точки масс путем возведения значения функции Гамильтона 3 в уравнение 4.4 RFE RL п н г доктор РФ 0.Задача 17.16.Если P-его вес, то для составления стандартного уравнения движения физического маятника, 1g — момент инерции к оси усиления, r, OS a-расстояние от точки усиления O до центра. Л По вопросу 17.15.Тяжесть от маятника см. фото. Игнорируйте 3-й.

Выберите угол поворота p в качестве обобщенной координаты. Решение. Маятник представляет собой систему с 1 степенью свободы, так как его положение определяется углом наклона rotation .To вычислите сопряженный обобщенный импульс rf, опишите кинетическую энергию маятника. Т Л Р.1 Тогда мы получаем dT, для сопряженного обобщенного импульса. РЗ ИБ м от 2 3 Единственная действующая сила-гравитация Р — это потенциал, а связь-ось усиления-идеальна и неподвижна.

Таким образом, функция Гамильтон равен полной механической энергии маятника Я Г П 4 Потенциальная энергия маятника П пу — Пасуш п.5 Если ввести результат 1 и 5 в Формулу 4 Y4Ф2-Pa cos p. 6 Напомним, что эта формула для H не может быть использована для создания канонического уравнения, так как Гамильтонова функция должна быть выражена в соответствии с обобщенными координатами и импульсом. Используйте уравнение 3, чтобы исключить обобщенную скорость из уравнения 6.2 РЧ-Ра со Ф.7 В этом случае форма канонического уравнения имеет вид День ду Введя значение функции Гамильтона 8 в уравнение 7, получим искомое уравнение движения физического маятника.— peslnqi.

Стандартное уравнение 9 эквивалентно 2-му-1-му дифференциальному уравнению. Первое уравнение 9 получается путем дифференцирования по времени и исключения rf из 2-го уравнения 9 дифференциального уравнения качания маятника. РФ — па грех Ф. Задача 17.16.Используйте каноническое уравнение Гамильтона для получения закона сохранения полной механической энергии.

По формуле, приведенной в подразделе 2 этого раздела 5, было показано, что Гамильтонова функция H в случае голономной системы зависит, вообще говоря, от времени, обобщенных координат, обобщенного импульса. ГБ Пи, 1 Где 1 1, 2, .. S — число степеней свободы в материальной системе. Вычислить производную по времени функции 1 dh dn. ОТЛИЧИТЕЛЬНОЕ ИМЯ. День. День. .отличительное имя. День. День Используя нормальное уравнение Он также заменяет p Формулы 2.З.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

гамильтона уравнения

ГАМИЛЬТОНА УРАВНЕНИЯ (канонические уравнения механики) — дифференциальные ур-ния движения голономной механич. системы в канонич. переменных, к-рыми являются s обобщённых координат q_i и s обобщённых импульсов p_i, где s — число степеней свободы системы. Выведены У. P. Гамильтоном (W. R. Hamilton) в 1834. Для составления Г. у. надо в качестве характеристич. ф-ции системы знать Гамильтона функцию Н(g_i, р_i, t), где t — время. Тогда, если все действующие на систему силы потенциальны, Г. у. имеют вид

Если наряду с потенциальными на систему действуют непотенциальные силы F, то к правым частям 2-й группы ур-ний (*) надо прибавить соответствующие обобщённые силы Q_i. Ур-ния (*) представляют собой систему 2s обыкновенных дифференц. ур-ний 1-го порядка, интегрируя к-рые можно найти все q_i и p_i как ф-ции времени t и 2s постоянных интегрирования, определяемых по нач. данным. Решение системы ур-ний (*) можно также свести к отысканию полного интеграла соответствующего ей ур-ния в частных производных (см. Гамильтона — Якоби уравнение).

Если одна из координат q_i, напр. q₁, является циклич. координатой, т. е. явно не входит в выражение ф-ции Н, то =0 и одно из ур-ний (*) даёт сразу интеграл , где — постоянная. Особый интерес представляет случай, когда все координаты циклические, а ф-ция явно не зависит от времени (силовое поле и наложенные связи стационарны). Тогда все , т. е. постоянны; следовательно, ф-ции и тоже постоянны, и 1-я группа ур-ний (*) даёт , откуда , где , C_i — новые постоянные. Ур-ния в этом случае интегрируются элементарно и все координаты являются линейными ф-циями времени. Отсюда следует, что задачу интегрирования Г. у. можно свести к задаче отыскания для системы циклич. координат. Это, в принципе, возможно, т. к. Г. у. обладают тем важным свойством, что они допускают переход с помощью т. н. канонических преобразований от переменных q_i, р_i к новым переменным Q_i(q_i, р_i, t), P_i(q_i, р_i, t), которые также являются каноническими и удовлетворяют уравнениям (*) с соответствующей функцией H(Q_i, P_i, t).

Равноправность в Г. у. координат и импульсов как независимых переменных, а также инвариантность этих ур-ний по отношению к канонич. преобразованиям открывают большие возможности для обобщений. Поэтому Г. у. имеют важные приложения не только в механике, но и во многих др. областях физики, напр. в статистич. физике, квантовой механике, электродинамике и др.

Лит. см. при ст. Динамика, Действие. С. M. Тарг.