Функция грина уравнения лапласа в

Лекция 9. Функция Грина. Примеры

В этой лекции мы будем рассматривать уравнение Лапласа в ограниченных областях D, расположенных на плоскости или в пространстве. Точки Р(х, у) и Р_o (х_o , у_o ) на плоскости (или Р(х, у, z) и в пространстве) принадлежат области D и
(или
) — расстояние между точками Р_o и Р.
Предположим, что на границе области D задано нулевое условие Дирихле.

Функция G(P,P_o) называется функцией Грина задачи Дирихле в области D, если для любой фиксированной точки она, как функция от Р , удовлетворяет следующим условиям:

(i) непрерывная в всюду, кроме точки P_o, и G(P,P_o ) = 0 на границе D;
(ii) гармоническая в D за исключением точки P_o;
(iii) в случае плоскости остается гармонической функцией в точке P_o; в случае пространства функция остается гармонической в точке P_o.

Как следует из определения, функция Грина непрерывна и гармонична всюду в области D за исключением точки P_o, в которой она имеет особенность типа в плоскости или в пространстве. Функцию Грина иногда называют функцией источника.

Функция Грина G(P,P_o) (если она существует) однозначно определяется свойствами (i)-(iii). Кроме того, в области D. Рассмотрим, к примеру, плоскую область D. Для того, чтобы доказать единственность функции Грина, предположим противное: пусть G₁, и G₂ — две функции, обладающие свойствами (i)-(iii) для заданных области D и точки . Тогда ( G₁ — G₂ ) остается гармонической в любой точке области D, включая и точку P_o, поскольку вблизи точки P_o можно записать

Каждая скобка в правой части (41) представляет собой функцию, гармоническую всюду в D (см. свойство (iii)), поэтому и разность ( G₁ — G₂ ) — функция гармоническая всюду в D. Кроме того, на границе D функция Следовательно, по принципу максимума в области D.

Далее, если D₁ — часть области D, находящаяся вне малой окрестности точки P_o, то, согласно условиям (i)-(iii), функция G непрерывна в гармонична в D₁, и на границе D₁ принимает неотрицательные значения (так как при ). Поэтому по принципу максимума в D₁ причем нулевое значение внутри области D₁ функция принимать не может. Это означает, что всюду в D.

Пример 1. На плоскости рассмотрим круг радиуса R с центром в начале координат. Построим функцию Грина в круге. При построении этой функции нам понадобится понятие сопряженных точек. Точки P_o и Р * называются сопряженными относительно окружности, если они лежат на одном луче, исходящем из центра O окружности, и произведение их расстояний от центра равно квадрату радиуса: (см. рис.16).

Обозначим через r_o =|OP_o| и r * =|OP * |. Тогда r_o r * =R 2 . Так как точки P_o и Р лежат на одном луче, выходящем из начала координат, то

По теореме косинусов и , где ρ=|OP|.

Рис. 17
Воспользовавшись равенством r_o r * =R 2 , получим 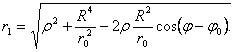Таким образом, величины r и r₁ выражаются через R, ρ, r_o, φ, φ_o, и, в конечном счете, через R, x, y, x_o, y_o. Покажем, что функция G(P,P_o) удовлетворяет пунктам (i)-(iii) определения. Очевидно, что функция непрерывна всюду в замкнутом круге кроме точки Р_о (когда r = 0). На границе круга расстояние ρ=R и, следовательно,

Отсюда Функция G(P,P_o) состоит из двух слагаемых. Первое слагаемое-фундаментальное решение уравнения Лапласа и,следовательно, гармоническая функция всюду, кроме точки P_o. Функция является гармонической всюду в области D , так как точка Р принадлежит области, а точка Р * лежит вне области D и, следовательно, r₁ >0. Гармоничность этой функции легко проверяется, если записать оператор Лапласа в полярной системе координат с полюсом в точке Р * (см.аналогичную формулу (33*) с полюсом в точке О):

Поэтому функция G(P,P_o) гармоническая в области D всюду, кроме точки Р_о, а разность G(P,P_o) — ln(1/r) — гармоническая и в точке Р_о.

Аналогично строится функция Грина для шара радиуса R. Она имеет вид где r=|P_oP| , r₁=|PP * | , r_o=|OP_o|. Точка P * (x * , y * , z * ) сопряженная точке Р_o (х_o , у_o , z_o ) относительно сферы радиуса R с центром в точке О, то есть . Координаты x * , y * , z * вычисляются по формулам:

Пример 2. Функцию Грина можно рассматривать не только для ограниченных, но и для неограниченных областей. В качестве примера построим функцию Грина для полуплоскости. Для этого определим точки, сопряженные относительно прямой: точки Р_о и Р * называются сопряженными относительно прямой, если они симметричны относительно этой прямой (см. рис.18).

Функция где
,
(см. рис.19), удовлетворяет свойствам (i)-(iii) в полуплоскости у > 0. В самом деле, на границе области при у = 0 расстояние r = r₁, поэтому Гармоничность функции всюду в области у > 0 проверяется непосредственно вычислением частных производных:

Следовательно, функция G(P,P_o) гармоническая в области у > 0 всюду, кроме точки Р_о, а разность G(P,P_o) — ln(1/r) гармоническая и в точке Р_о.

Для полупространства z > 0 функция Грина имеет вид где

Функция грина уравнения лапласа в

Интеграл Дирихле, первая, вторая и третья формулы Грина. Гармонические функции и их свойства, теоремы о гармонических функциях. Шаровые и сферические функции. Дифференциальное уравнение для сферических функций и его решение.

В данном разделе перечислим без вывода основные формулы теории потенциала, которые находят применение в теории фигуры Земли. Остановимся лишь на некоторых, наиболее важных теоремах.

Введем векторный оператор набла :

, где — единичные, взаимно ортогональные вектора. С векторным оператором можно обращаться, как с обыкновенным вектором. Например, скалярное произведение двух операторов набла дает оператор Лапласа: .

Допустим, что в нашем распоряжении имеется некоторая скалярная функция . Тогда

С помощью оператора Лапласа интегрирование по объему можно заменить интегрированием по поверхности. В дальнейшем для обозначения пределов интегрирования мы будем использовать следующий прием. Все двукратные или трехкратные интегралы мы будем изображать однократным интегралом. Под интегралом будем использовать символ ( ) если интегрирование ведется по телу, ограниченному поверхностью , или просто значком , если интегрирование ведется по поверхности . С этими где оговорками формула Остроградского (3.1) принимает вид

где — элемент объема, — элемент поверхности, а буквой обозначена внешняя нормаль.

3.1.2 Первая формула Грина

Введем обозначение оператора

тогда первая формула Грина примет вид

Интеграл по объему от функции называется интегралом Дирихле:

Очевидно, что в формуле Грина функции и можно менять местами, то есть вместо (3.3) можно написать

Вычитая левые и правые части формул (3.3) и (3.5), получим вторую формулу Грина

Рассмотрим частный случай, когда , где — расстояние между двумя точками P(x,y,z) и Первая точка имеет фиксированные координаты, а вторая — принадлежит телу и имеет текущие координаты, принадлежащие элементу объема. Тогда

Нетрудно убедиться, что для , имеет место равенство . Имеем

Проделаем следующие выкладки

Обратимся снова к второй формуле Грина. Перепишем ее для случая, когда . Возможны три варианта, когда точка лежит вне тела, внутри его и на поверхности, которое ограничивает это тело.

Точка Р — внешняя. В этом случае во всем внутреннем пространстве тела, по которому ведется интегрирование, радиус-вектор r не обращается в нуль и . Вторая формула Грина (3.6) принимает вид

Мы получили третью формулу Грина для внешней точки.

Точка Р — внутренняя. В одной точке внутреннего пространства радиус-вектор обращается в нуль и функция обращается в бесконечность. Опишем вокруг этой точки сферу с малым радиусом. Интегрирование по телу, ограниченному поверхностью , можно разбить на два этапа: интегрированию по всем точкам тела, исключая малую сферу, содержащую точку , и интегрирование по малому шару, ограниченному малой сферой :

где — тело с выколотой точкой . Поскольку во всем внутреннем пространстве , то первое слагаемое в правой части полученной формулы обращается в нуль, так как . Займемся вторым слагаемым. Будем считать, что радиус малой сферы настолько мал, что функцию внутри этой сферы — постоянная величина. Тогда

Воспользуемся формулой Остроградского, в которой положим , тогда вместо интегрирования по объему будем интегрировать по поверхности малой сферы

Отношение есть элементарный телесный угол , под которым «виден» из точки элемент поверхности сферы. Понятно, что, если точка находится внутри этой сферы, то рассматриваемый интеграл будет равен полному телесному углу, по которым видна поверхность сферы изнутри. Очевидно, что он равен , то есть

Перепишем формулу (3.6) в следующем виде

В случае , для внешней точки получим

Точка P лежит на поверхности. Третий случай — это когда точка не является ни внутренней ни внешней: она лежит на поверхности тела. Можно показать, что в этом случае

noindent поэтому третья формула Грина принимает вид

Формулы (3.7), (3.8) и (3.9) можно записать одной формулой

Гармонической функцией координат называется функция, непрерывная вместе со своими первыми и вторыми производными в некоторой области , удовлетворяющая во всех точках этой области уравнению Лапласа .

Линейная комбинация двух и более гармонических функций есть функция гармоническая.

Пусть U(x,y,z) и V(x,y,z) — две гармонические функции, то есть и . Возьмем их линейную комбинацию . Очевидно, что . Поскольку , , то и , что и доказывает наше утверждение.

Если — гармоническая функция, то все ее частные производные гармонические функции. Доказательство основано на взаимной переставимости оператора Лапласа и производных. Пусть

Линейное преобразование координат (поворот осей, изменение масштаба) не нарушает свойство гармоничности.

Пусть — гармоническая функция. Введем новые координаты

В матричном виде приведенное равенство выглядит следующим образом

Подставим в функцию линейные выражения для , , , для чего воспользуемся вторым из приведенных выше равенств, получим V( . Докажем, что если функция гармоническая, то и является гармонической функцией.

Запишем полученные равенства в матричной форме

Поскольку оператор Лапласа есть квадрат векторного оператора набла , то

В правой части будем иметь

Поскольку матрицы направляющих косинусов являются ортонормированными, их произведения равны единичной матрице и оператор Лапласа принимает вид

Отсюда следует, что оператор Лапласа является инвариантом по отношению к повороту осей, а при изменении масштаба множителем с изменяется на множитель . Другими словами, если , то .

3.2.2 Теоремы о гармонических функциях

Теорема Гаусса: Поток градиента гармонической функции через замкнутую поверхность равен нулю. Потоком называется интеграл по заданной поверхности от нормальной производной функции.

Пусть — гармоническая функция. Предположим, что задана замкнутая поверхность S, ограничивающая область, внутри которой эта функция — гармоническая. Тогда, используя формулу Остроградского (3.1), получим

Но так как функция гармоническая, то , поэтому

В случае, когда — потенциал притяжения, то справедливо уравнение Пуассона , где — плотность притягивающих масс. Тогда формула (3.1) приводит к формуле Гаусса.

Гармоническая функция в замкнутой области D не имеет ни минимума, ни максимума.

Преположим обратное: внутри области существует точка , в которой гармоническая функция имеет максимум. В малой окрестности этой точки на сфере нормальная производная функции будет отрицательной, тогда , что противоречит теореме Гаусса.

textitПотенциал притяжения вне притягивающих масс не может иметь ни минимума, ни максимума; внутри этой области может иметь только максимум.

Любая область вне притягивающего тела есть область определения гармонической функции, внутри которой, согласно теореме 2, не может иметь ни минимума, ни максимума. Предположим обратное: внутри притягивающего тела существует точка , в которой потенциал притяжения достигает минимума. В этой точке справедливо уравнение Пуассона . По формуле Остроградского будем иметь

Mы пришли к противоречию: вследствие минимума внутри малой сферы, нормальная производная на поверхности этой сферы будет положительной, следовательно и приведенные выше интегралы будут положительны, что противоречит сделанному выше выводу. Таким образом, теорему можно считать доказанной.

Теорема Гаусса. Значение гармонической функции в центре сферы равно среднему из значений этой функции на поверхности.

Обратимся к третьей формуле Грина, когда точка внутренняя. Для гармонической функции , поэтому на сфере формула (3.8) принимает вид

На поверхности сферы нормальная производная совпадает с производной по радиус-вектору, поэтому

Кроме того, на поверхности сферы , поэтому

но согласно теореме Гаусса о потоке первое слагаемое в полученном выражении равно нулю, то есть

что и требовалось доказать.

Шаровой функцией степени называется гармоническая функция, являющаяся однородным степенным полиномом вида

где — постоянные. Возьмем сферическую систему координат

где — долгота, — полярное расстояние, — радиус-вектор точки . Очевидно, что

называется сферической функцией .

Итак, шаровая функция степени имеет вид

Существует и другой класс шаровых функций, который приведем здесь без вывода

где — та же сферическая функция, которая входит и в формулу (3.16).

Число постоянных шаровой функции степени равно . Убедимся в этом на при мере шаровой функции третьей степени:

Всего однородный полином третьей степени имеет 10 постоянных. Однако не все постоянные независимы. Шаровые функции подчиняются уравнению Лапласа. Выполнив необходимые выкладки, получим

Следовательно, из 10 постоянных 3 линейно связаны уравнением Лапласа. Остается 10-3=7 независимых постоянных.

Поскольку шаровые функции удовлетворяют уравнению Лапласа, то есть

то должны выполняться и уравнения

В последнем варианте шаровые функции записаны в сферических координатах, поэтому нам необходимо уравнение Лапласа переписать также в сферических координатах.

Из дифференциальной геометрии известно, что если , , — обобщенные координаты, то элемент дуги в этой системе координат будет иметь вид

где , , — коэффициенты Ламе:

Теперь оператор Лапласа можно определить следующим образом (без вывода)

Определим коэффициенты Ламе для сферической системы координат. В данном случае , , , поэтому

Оператор Лапласа для сферических координат будет выглядеть так

Применим этот оператор к шаровой функции вида Очевидно, что оператор Лапласа для шаровой функции равен нулю, поэтому

Таким образом, дифференциальное уравнение для сферической функции порядка имеет вид

Предлагаем самостоятельно убедиться в том, что дифференциальное уравнение для функции входящую в шаровую функцию второго рода совпадает с уравнением (3.20).

Заменим переменную на . тогда . Очевидно, что

поэтому дифференциальное уравнение (3.20) можно переписать так

Будем искать решение этого уравнения в виде . Подставив это выражение в дифференциальное уравнение, будем иметь

Умножив каждый член полученного выражения на и поделив на , получим

Видим, что первые два члена зависят только от , а последний — только от Для того, чтобы уравнение выполнялось для любых и , необходимо, чтобы эти функции выродились в константы. Например, уравнение будет выполняться, если

Второе уравнение есть уравнение гармонических колебаний

Его решение для любых действительных значений имеет вид

где и — постоянные интегрирования. Решение первого из приведенных выше уравнений, зависит как от постоянной , так и от постоянной . Обозначив решение через , получим

Функция при целочисленных значениях носит название присоединенной (ассоциативной) функции Лежандра. В случае , эти функции становятся степенными полиномами, которые называются полиномами Лежандра. Полагая в уравнении (3.23) , получим дифференциальное уравнение для полиномов Лежандра

В теории специальных функций свойства функций и полиномов Лежандра достаточно хорошо изучены. Приведем лишь некоторые сведения (без вывода), которые могут пригодиться в нашем курсе. Присоединенные функции Лежандра и полиномы Лежандра связаны между собой соотношением

Подводя итог сказанному, выпишем окончательный вид решения дифференциального уравнения для сферических функций

Заметим, что порядок производной в (3.25) не может быть больше степени полинома Лежандра. По этой причине постоянные и называют степенью и порядком сферических функций.

О сходимости функции Грина уравнения Лапласа Текст научной статьи по специальности « Математика»

Похожие темы научных работ по математике , автор научной работы — Нажалов А. И., Нажалов М. А.

Текст научной работы на тему «О сходимости функции Грина уравнения Лапласа»

А.И. Нажалов, М.А. Нажалов

О сходимости функции Грина уравнения Лапласа

Для нахождения кулоновского потенциала в кристаллах широко используется функция Грина (ФГ) уравнения Лапласа. Она удовлетворяет уравнению

АОь (г, г’) = 8 (г — г’), (1)

где 8 — дельта функция Дирака; Оь — функция Грина.

Явный вид этой функции хорошо известен

В этом выражении О — объем элементарной ячейки кристалла, К — вектор обратной решетки.

Сумма по решетке в (2) сходится условно, и в таком виде она для практических целей непригодна. Чтобы ряд стал абсолютно сходящимся, применяются различные методы улучшения их сходимости. Здесь мы не будем обсуждать эти методы, а сразу воспользуемся результатами работы [1], где это улучшение проведено. Результат можно представить в виде

Оь(г,г’) = Ок + Ок , (3)

pKо — exp(-pKp )Sh(Kоp)

В этих выражениях р = — г — г’| — вектор

прямой решетки; к — параметр сходимости.

Как видно из (4), сходимость суммы по обратной решетке обеспечивается экспоненциальным множителем. Чтобы выяснить сходимость суммы по прямой решетке, выражение (5) преобразуем к виду

Gr (r, r’) = —— У — R 4p ”

При больших значениях векторов решетки Я переменной у в числителе и единицей в знаменателе по сравнению с гиперболическими функциями можно будет пренебречь, тогда выражение в квадратных скобках под знаком суммы

примет вид —————, т.е. и сумма по прямой

решетке имеет экспоненциальную сходимость.

Цель настоящей работы — определение параметра сходимости таким образом, чтобы он обеспечивал примерно одинаковый объем вычислений как по прямой решетке, так и по обратной. Кроме того, окончательное значение результата суммирования функции Грина не должно зависеть от параметра сходимости.

Выбор параметра сходимости осуществим для двух типов решеток: кубических и гексагональной плотноупакованной (ГПУ). Это позволит распространить выводы о сходимости решеточных сумм на другие типы кристаллов. Начнем с кубических решеток.

Из трех типов кубических решеток — простой кубической (ПК), объемно-центрированной (ОЦК) и гранецентрированной (ГЦК) — наихудшей сходимостью обладают решеточные ряды для (ПК), так как радиусы ее координационных сфер убывают медленнее, чем у других кубических решеток. Кроме того, число узлов, а следовательно, и число слагаемых в сумме также растет быстрее с ростом номера координационной сферы. В прямом пространстве длины векторов будем измерять в единицах постоянной решетки а, в обратном — в единицах 2п/а. Сходимость суммы по обратной решетке: выражение (4) будет

множителем exp(-p^fn /ко),

прямой решетке (5) — множителем ехр(-4жк04п). В обоих случаях п — номер координационной сферы.

Если выбирать параметр к0 из условия одинаковой сходимости рядов как по прямой, так и по обратной решетке, то необходимо приравнять показатели обеих экспонент, что для параметра к0 дает теоретическое значение, равное 0.5. Практически сходимость исследовалась следующим образом:

а) простая кубическая решетка.

Вычисления выполнялись в 103 точках для трех направлений [100], [110], [111], которые в дальнейшем будем обозначать цифрами 1, 2, 3 соответственно. Для каждой координаты независимо от направления выбирался одинаковый шаг Н = 5.10-4.

Значения составляющих функции Грина для ПК решетки к0 = 0.25

1 0.3332487 0.3332487

1 2 0.3332487 0.3332487

ri 3 0.3332487 0.3332487

IIK 1 0.3333057 0.3333057

103 2 0.3333615 0.3333615

3 0.3334612 0.3334161

1 -159.24055 -159.25995 -159.261555 -159.26195

1 2 -112.62515 -112.64455 -112.646158 -112.64655

3 -91.97376 -91.99316 -91.994769 -91.995160

‘-‘R 1 -0.2968489 -0.322368 -0.3245311 -0.3250639

10J 2 -0.2515340 -0.282707 -0.2855016 -0.2861946

3 -0.2277178 -0.264115 -0.2676635 -0.2685483

1 -158.907309 -158.926704 -158.928309 -158.928701

1 2 -112.291909 -112.311304 -112.312909 -112.313301

3 -91.640521 -91.659915 -91.661520 -91.661912

‘-’L 1 0.03645681 0.010937386 0.008775 0.0082418

103 2 0.08182750 0.050653692 0.04785984 0.0471167

3 0.1056182 0.069301050 0.065752555 0.0648677

Численно параметр сходимости принимался равным трем значениям 0.25, 0.5, 0.75. Для первого значения результаты расчета представлены в таблице 1.

В первой колонке записаны составляющие функции Грина, во второй — номера .М-точек (первой и последней), которым соответствуют строки направлений (1, 2, 3) — третья колонка г. Колонки, обозначенные цифрами 1, 7. дают число сфер, которые включались в суммы, причем первые две «строки» Ок дают сумму по обратной решетке, вторые две — сумму по прямой решетке, последние две «строки» — суммарный результат. Многоточие в 9 и 11-й колонках обозначает совпадение результатов с предыдущими колонками.

Обсудим результаты этого расчета.

Во-первых, следует отметить очень хорошую сходимость суммы по обратной решетке: при заданном значении к0. Слагаемые в сумме убывают по экспоненциальному закону ехр(-4я л/й). Эта хорошая сходимость видна и из результатов расчета, которые показывают их незначительное изменение при суммировании от первой сферы до девятой. В то же время результаты расчета по прямой решетке показывают их плохую сходимость — особенно для граничных точек (см. «строку» ОЯ). Действительно, сходимость по прямой решетке определяется множителем только ехр(-Ял/п). Поэтому и окончательные ре-

Значения составляющих функции Грина ПК решетки к0 = 0.5

1 0.07208673 0.07023080 0.07023053 0.07023052

1 2 0.07208675 0.07023082 0.07023057 0.07023055

r’ 3 0.07208676 0.07023085 0.07.023060 0.07023057

lJK 1 0.07958445 0.08026239 0.08026234 0.08026236

103 2 0.08708220 0.08747233 0.08747241 0.08747239

3 0.09457995 0.09306246 0.09306265 0.09306262

1 -158.997724 -158.999376 -158.999376 -158.999376

1 2 -112.382324 -112.383976 -112.383976 -112.383976

3 -91.730935 -91.732587 -91.732588 -91.732588

VR 1 -0.06878756 -0.07262748 -0.07262821 -0.07262828

10J 2 -0.02897386 -0.04111476 -0.04111657 -0.04111674

3 -0.01436645 -0.02924194 -0.02924611 -0.02924647

1 -158.925637 -158.929145 -158.929146

1 2 -112.310237 -112.313745 -112.313746

3 -91.658849 -91.662356 -91.662357

1 0.01079689 0.007634956 0.007634138 0.00763407

103 2 0.05810833 0.04635757 0.04635584 0.04635564

3 0.08021350 0.06382051 0.06381649 0.06381615

зультаты суммирования неустойчивы. Отсюда можно сделать вывод, что значение к0 = 0.25 не является удовлетворительным. Приведем таблицу для к0 = 0.5.

Анализ таблицы позволяет сделать вывод, что для данного параметра сходимости суммирование по обратной решетке для достижения точности не менее пяти значащих цифр как для начальной точки, так и граничной можно вести до восьмой координационной сферы. Эта точность, даже несколько лучше, обеспечивается и для прямой решетки.

При использовании методики улучшения сходимости решеточных рядов как в настоящей работе, так и любой другой окончательная сумма ряда не должна зависеть от параметра сходимости — результаты расчета в последних двух клетках обеих таблиц должны совпадать. Однако удовлетворительное согласие наблюдается только для первой точки. Чтобы выяснить эту проблему до конца, приведем еще таблицу для к0 = 0.75 и координационных сфер с 5-й по 13-ю.

Данные последней таблицы позволяют сделать два вывода.

Во-первых, увеличение параметра к0 приводит к ухудшению сходимости суммы по обратной решетке. Из первых двух «строк» таблицы видно, что устойчивого результата суммирования не получается даже при учете тринадцатой координационной сферы (всего пять — шесть значащих цифр). В то же время по прямой решетке для достижения этой же точности достаточно включать в сумму только пять сфер.

Во-вторых, из сравнения двух последних «клеток» таблиц для разных параметров сходи-

мости можно сделать вывод, что с точностью в шесть значащих цифр для малого значения вектора г- (первая точка) результаты суммирования не зависят от параметра сходимости. Это же можно сказать и о точности для последней точки.

б) ГПУ структура.

С точки зрения исследований этой работы основной особенностью ГПУ решетки является то, что эта решетка при любом выборе основных векторов трансляции имеет базис. Кроме того, она характеризуется двумя параметрами а и с

или их отношением с к а, У = —.

Базисные векторы выберем в таком виде [2] а1 = аі , а1 = а(1,0,0), а2 = 0.5а(-і +^ъ]),

а2 = а(-0.5,0.5^/30), а3 = ск = аук = а(0,0,у),

где і, ], к — орты декартовой системы координат. Тогда векторы целочисленных трансляций прямой решетки Яр могут быть представлены в виде

= Ргаг + Р2а2 + РА> где р>, р2, р3 — целые положительные и отрицательные целые числа, включая нуль. Суммирование по этим векторам будем называть суммированием по основной решетке.

Базис, состоящий из двух узлов, обозначим векторами ^ и £2, причем ^ = (0,0,0),

а ґ2 = — а1 + — а2 + — а3 = —;= ] + 0.5аук

Суммирование, определяемое вектором Яр + і2, будем называть суммированием по сдвинутой подрешетке. Базисные векторы обратной

Значения составляющих функции Грина ПК решетки Kg = 0.75

GK 1 1 -0.02304124 -0.02351801 -0.02352996 -0.02353722

2 -0.02304109 -0.02351787 -0.02352952 -0.02353607

3 -0.02304096 -0.02351772 -0.02352937 -0.02353692

103 1 0.02951775 0.02959479 0.02960289 0.02960377

2 0.05289110 0.05299915 0.05298750 0.05298991

3 0.06720290 0.06681912 0.06682722 0.06682556

Gr 1 1 -158.905608 -158.905608 -158.905608 -158.905608

2 -112.290208 -112.290208 -112.290208 -112.290208

3 -91.638820 -91.638820 -91.638820 -91.638820

103 1 -0.02196870 -0.02196872 -0.02196872 -0.02196872

2 -0.006633888 -0.00663402 -0.00663402 -0.006634024

3 -0.003010426 -0.00301113 -0.00301113 -0.003011134

gl 1 1 -158.928649 -158.929126 -158.929138 -158.929145

2 -112.313249 -112.313726 -112.313738 -112.313745

3 -91.661861 -91.662338 -91.662349 -91.662357

103 1 0.00754905 0.007626070 0.007634170 0.007635045

2 0.04625722 0.004636512 0.004635348 0.04635589

3 0.0641925 0.06380799 0.06381609 0.06381442

решетки также легко получаются. Им соответствуют выражения [2]

Вектор же трансляции обратной решетки при заданном базисе может быть записан в виде

Кп = п1ь1 +П2Ь2 + П3Ь3.

Поскольку длины векторов ГПУ решетки определяются отношением 7, то и сходимость решеточных сумм, очевидно, будет зависеть от этого параметра. Имея в виду, что дальнейшие вычисления для решеток этого типа предполагается выполнить для Т1, Со и Еп и так как каждый из металлов имеет свою величину 7, сходимость исследуем на примере Ть Для него 7 = 1.587306 [3]. Из-за этого параметра в кристаллах ГПУ квадраты длин векторов трансляций не обязаны быть целочисленными. Поэтому все суммирования по решетке выполняют, как правило, внутри сферы заданного радиуса. В нашем случае этот радиус принимался равным нескольким значениям. Во-первых, для кубических решеток необходимо было вычислять по векторам, находящимся в области до десяти координационных сфер, что соответствовало радиусу прямой решетки равным 5.0 в единицах постоянной решетки. Здесь поступали аналогично: перебирали целые значения совокупности р, р, р3

от -11 до 11, так чтобы |^р| £ 5.0 , что давало в сумме по двум подрешеткам 868 узлов. Точно так же поступали и с обратной решеткой — получали 710 узлов. Параметр сходимости к0 так же, как и для кубических решеток, равнялся трем значениям: 0.25, 0.5, 0.75. Вычисления функции Грина велись в четырех направлениях: первое направление — вдоль оси х, второе — вдоль оси у, третье — вдоль оси г, четвертое — вдоль вектора t. Эти направления будем обозначать цифрами 1, 2, 3 и 4 соответственно. Для всех направлений использовался один и тот же шаг Н = 5.0-10-4, но с разным их количеством. Так, для первого направления Ы1 = 1000, второго — Ы2 = 1732, третьего — Ы3 = целая часть10007, четвертого направ-

ления — N 4 = целая часть -1—- . Такое число ша-

гов обеспечивает вычисления вплоть до середины расстояния между узлами в каждом из направлений. Следует заметить, что для четвертого направления шаги ку, Ъг вдоль осей у и г выбирались так, чтобы имело место соотношение

ку + кг = Н. Результаты для к0 = 0.25 представлены в таблице 4. В первой колонке таблицы приведены номера точек, в которых проводи-

лись вычисления: первая последняя, во второй -номера направлений, в третьей — результат суммирования функции Грина по прямой решетке, в четвертой — по обратной решетке, в пятой колонке — полная сумма.

Значения составляющих функции Грина для ГПУ решетки к0 = 0.25

1 1 -159.3794992 0.484963494 -158.8945357

2 -159.3794992 0.484963494 -158.8945357

3 -159.3794992 0.484963494 -158.8945357

4 -159.3795291 0.484963494 -158.8945656

N, 1 -0.45005495 0.484973943 0.0349189892

N? 2 -0.45004724 0.484973942 0.0349266980

N3 3 -0.41635845 0.484976435 0.0433459028

N4 4 -0.45378068 0.484971525 0.3119084080

Аналогичные результаты представлены в таблицах 5 и 6, но для к0 = 0.5 и 0.75 соответственно.

Значения составляющих функции Грина для ГПУ решетки к0 = 0.5

1 1 -159.0096602 0.115115962 -158.894544

2 -159.0096602 0.115115962 -158.894544

3 -159.0096602 0.115115961 -158.894544

4 -159.0096901 0.115115962 -158.894574

N, 1 -0.086955700 0.121862557 0.0349068572

N?. 2 -0.086955905 0.121862449 0.0349065445

N1 3 -0.078576731 0.121892677 0.0433159465

N4 4 -0.090187518 0.121348447 0.0311796634

Значения составляющих функции для ГПУ решетки к0 = 0.75

Таблица 6 Грина

1 1 -158.9063832 0.0118390288 -158.894544

2 -158.9063832 0.0118390288 -158.894544

3 -158.9063832 0.0118396263 -158.894544

4 -158.9064131 0.0118390271 -158.894774

N, 1 -0.023566793 0.058467654 0.0349068669

N2 2 -0.023560847 0.058467396 0.0349065433

N3 3 -0.017720496 0.061036432 0.0433159354

n4 4 -0.025360450 0.056540083 0.0311796332

Внимательное сравнение всех трех таблиц показывает, что хотя результаты суммирования по прямой и обратной решетке для различных значений параметров сходимости заметно отличаются друг от друга, суммарный результат (последняя колонка) уже проявляет признаки сходимости. Особенно это заметно для первой точки. Кроме того, отчетливо проявляется независимость результатов суммирования от параметра сходимости. Дальнейшее увеличение чис-

ла узлов по прямой решетке до 1448 — |^р| £ 6.0 и

по обратной решетке до 1224 узлов — |Кп| £ 6.0

показало несущественное изменение результатов в приведенных выше таблицах. Это изменение главным образом проявилось в большей устойчивости (совпадении большего числа значащих

цифр) сходимости суммарного результата. Еще один вариант вычисления |лр| Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

1. Нажалов А.И. Преобразование функции Грина 2. Джонс Г. Теория зон Бриллюэна и электронные

уравнений Шредингера и Лапласа для кристаллов состояния в кристаллах. М., 1968.

// Известия вузов. Физика. Томск, 1996. (Рукопись 3. Тонков Е.Ю. Фазовые диаграммы элементов

депонирована в ВИНИТИ рег. №1603-В99) при высоком давлении. М., 1979.