Функция полезности в уравнении слуцкого

Теоретический материал: Уравнение Слуцкого

Теоретический материал: Уравнение Слуцкого

Для описания декомпозиции изменения маршаллианского спроса в аналитической форме часто используется т. н. уравнение (или тождество) Слуцкого.

Чтобы упростить наши выкладки, будем считать, что:

— потребителю доступны два блага (1 и 2),

— его первоначальный оптимальный набор:

— доход потребителя – I, цена первого блага – p1, цена второго блага фиксирована и равна единице

–> чтобы упростить запись, мы не записываем цену второго блага в числе аргументов, т. к. она все равно не будет меняться

Тогда уравнение Слуцкого в простейшей форме можно записать так:

(1)

ЗАМЕТИМ, что это действительно тождество: вы можете привести подобные слагаемые в правой и левой частях уравнения, и убедиться, что оно выполняется для любых параметров p1, p1’, I и I’!

Если обозначить каждую из разностей в фигурных скобках как соответствующую Δ (как это делает, например, Хэл Вэриан), уравнение (1) примет вид:

(2)

Уравнение Слуцкого часто представляют в виде отношений изменений. Разделим обе части уравнения (2) на Δp1:

(3)

Теперь давайте преобразуем последнее слагаемое в правой части уравнения (3). При декомпозиции по Слуцкому, компенсация должна позволить потребителю при новых ценах приобрести свой первоначальный набор, то есть:

Подставив это в знаменатель последнего слагаемого уравнения (3), получим:

(4)

Рассматривая бесконечно малые изменения p1 и I, мы могли бы записать это уравнение в первых производных.

Вначале, рассмотрим левую часть уравнения (4):

(5)

Теперь рассмотрим первое слагаемое в правой части уравнения (4):

ОБРАТИТЕ ВНИМАНИЕ! В отличие от выражения (5), данный предел уже нельзя рассматривать как частную производную функции маршаллианского спроса по p1, т. к. одновременно c p1 меняется I! [1]

Выход состоит в следующем: введем функцию , которая будет показывать, сколько товара 1 потребитель приобретет при цене p1 и компенсированном по Слуцкому доходе I’ (заметим, что тогда I’ полностью задается уравнением –
поэтому-то мы и не указываем его в числе аргументов !).

(6)

è Будем называть функцию функцией компенсированного (по Слуцкому) спроса на товар 1.

ЗАМЕЧАНИЕ 1: При декомпозиции по Хиксу, мы используем аналогичный прием: вводим функцию компенсированного (по Хиксу) спроса на товар 1: .

ЗАМЕЧАНИЕ 2: Поскольку в курсах продвинутого уровня практически всегда используется именно декомпозиция по Хиксу, функцию компенсированного спроса часто обозначают как “h”, и называют «хиксианским спросом» (“hicksian demand”) – в противовес обычному («маршаллианскому»).

Наконец, рассмотрим второе слагаемое в правой части уравнения (4):

(7)

Имея уравнения (4), (5), (6) и (7), мы можем записать уравнение Слуцкого в дифференциальной форме:

(8)

ЗАМЕТИМ: между уравнениями (4) и (8) возникает некоторая натяжка: в то время как в уравнении (4) знак перед вторым слагаемым в правой части положителен, в уравнении (8) он отрицателен.

Формально, никакого противоречия здесь нет. ОДНАКО, чтобы СТАНДАРТИЗИРОВАТЬ запись уравнения Слуцкого, при записи уравнения Слуцкого в дискретной форме (уравнение (4)) экономисты рассматривают эффект дохода с обратным знаком:

Δx1I = = – Δx1N.

Если в уравнении (4) заменить Δx1N на Δx1I, мы получим канонический вид уравнения Слуцкого в дискретной форме:

(9)

Убедительно прошу вас придерживаться именно его, т. к. это профессиональный стандарт.

Задача 1. (из прошлого семинара)

Функция полезности потребителя задана формулой , а бюджетное ограничение формулой .

а) Найдите функцию спроса и функцию компенсированного спроса потребителя.

б) Найдите разложение величины на эффекты замещения и дохода.

Задача 2. (из прошлого семинара)

Товары и считаются абсолютно взаимодополняющими, и потребитель потреблял их в соотношении две единицы на одну единицу . Первоначально они стоили 1 и 8 рублей соответственно. Доход потребителя равен 560 руб. Цена на не изменилась, а на повысилась до 14 руб. Найдите изменение спроса на товар в силу эффектов замещения и дохода.

Студентка, любящая шоколад, может тратить 10 долларов в день. Этот доход она расходует на шоколад и другие товары. Переменная обозначает количество унций шоколада, которое она покупает в день, переменная обозначает количество покупаемых единиц композитного товара ценой в 1 доллар. Функция полезности студентки . В начале декабря шоколад стоил 0,5 доллара за унцию, но к Рождеству подешевел и стал стоить всего 0,2 доллара. Найдите изменение потребления шоколада в силу эффекта замещения и эффекта дохода, вызванное его удешевлением.

[1] А это противоречит определению частной производной функции многих переменных.

Функции спроса, уравнение Слуцкого

Пусть р – цена товара X, q – цена товара Y, R – доход потре­бителя. Напомним, что функцией полезности U(x, у) называется функция, задающая степень полезности (для потребителя) набора товаров, состоящего из х единиц товара Х и у единиц товара Y. Будем считать, что потребитель может покупать только такие наборы (х, у), стоимость которых не превосходит его дохода, т.е. рх + qy£ R.

Определение. Пусть функция полезности U(x,y), при любых положительных р, q и R имеет на множестве

единственную точку глобального максимума (х*; у*). Тогда х*; у* – функции от р, q и R: х* = x D (p,q,R), y* = y D (p,q,R).

Эти функции называютсяфункциями спроса.

Смысл данного определения в том, что потребитель стремится к наибольшему удовлетворению от купленных им товаров при ограниченных средствах.

Для любого t > 0 функции спроса удовлетворяют следующим тождествам:

Таким образом, функции спроса являются однородными функциями степени однородности 0. Следовательно, для дифференцируемых функций спроса выполняются тождества Эйлера:

а также следующие уравнения для эластичности:

Функция Лагранжа запишется так:

Необходимые условия условного экстрему­ма (условия Куна-Таккера) для функции L(x,у) будут следующие:

U‘_x(х,у) – lр=0, U’_y(x,y) – lq =0,

l³0.

Если U’_x > 0 или U’_y > 0 (чаще всего выполняются оба условия), то тогда l можно исключить из системы. В итоге получаем систему уравнений

U‘_x(х,у)/U’_y(x,y)=р/q,

Первое выражение в (1.1.9) называют вторым законом Госсена. В общем виде он звучит так: максимум полезности обеспечивает такая структура покупок, при которой отношение предельной полезности каждого блага к его цене одинаково для всех благ.

Пpимер1.1.4. Найти функции спроса x D , y D в случае функции полезности

Решение. Для заданной функции полезности частные производные первого порядка таковы:

Система уравнений (1.1.9) имеет вид

U’_x/ U’_x=y 2 / x 2 =p/q,

Поэтому функции спроса таковы:

В заключение выведем уравнение Слуцкого для функций спроса. С этой целью преобразуем выражение q(x’_q + ух’_R). С учетом равенства

qx’_q = –рх’_р – Rх’_R , следующего из тождеств Эйлера (1.1.7), и равенства

qy = R – рх, вытекающего из бюджетного равенства рх + qy = R, имеем

Разделив первое и последнее выражения на q, получимуравнение Слуцкого:

Уравнение Слуцкого можно умножить на R/xy. Тогда оно приобретает вид

где Е_хq , Е_yp – перекрестные коэффициенты эластичности спроса, E_xR, E_уR – коэффициенты эластичности спроса по доходу, a=рх/R, b=qy/R – доли расходов на товары Х и Y в бюджете R..

Производственные функции.

Производственная функция (ПФ) выражает зависимость результата производства от затрат ресурсов. При описании экономики (точнее, ее производственной подсистемы) с помощью ПФ эта подсистема рассматривается как «черный ящик», на вход которого поступают ресурсы R₁, . R_n, а на выходе получается результат в виде годовых объемов производства различных видов продукции Х₁, . Х_m .

В качестве ресурсов (факторов производства) на макроуровне наиболее часто рассматриваются накопленный труд в форме производст­венных фондов (капитал) К и настоящий (живой) труд L, а в качестве результата – валовой выпуск Х (либо валовой внутренний продукт Y, либо национальный доход N). Во всех случаях результат коротко будем называть выпуском и обозначать X, хотя это может быть и валовой вы­пуск, и ВВП, и национальный доход.

Остановимся несколько подробнее на обосновании состава фактора К. Накопленный прошлый труд проявляется в основных и оборот­ных, производственных и непроизводственных фондах. Выбор того или иного состава K определяется целью исследования, а также характером развития производственной и непроизводственной сфер в изучаемый период. Если в этот период в непроизводственную сферу вкладывается примерно постоянная доля вновь созданной стоимости и непроизвод­ственная сфера оказывает на производство примерно одинаковое вли­яние, это служит основанием напрямую учитывать в ПФ только произ­водственные фонды.

Но производственные фонды состоят из основных и оборотных производственных фондов. Если соотношение между этими составными частями производственных фондов примерно постоянное в течение всего изучаемого периода, то достаточно напрямую учитывать в ПФ только основные производственные фонды.

Если изучаемый период достаточно продолжителен и однороден по влиянию на производство указанных выше составных частей, следует испробовать все варианты включения их в модель (от всех вместе до какого-то одного из них). Чтобы не вдаваться в детали, далее будем К называть фондами.

Таким образом, экономика замещается своей моделью в форме нелинейной ПФ

т.е. выпуск (продукции) есть функция от затрат ресурсов (фондов и труда).

Производственная функция Х=F(K,L) называется неоклассической, если она является гладкой и удовлетворяет следующим условиям, поддающимся естественной экономической интерпретации:

— при отсутствии одного из ресурсов производство невозможно;

2) ,

— с ростом ресурсов выпуск растет;

3) ,

— с увеличением ресурсов скорость роста выпуска замедляется;

— при неограниченном увеличении одного из ресурсов выпуск неограниченно растет.

Мультипликативная ПФ задается выражением

,

где А – коэффициент нейтрального технического прогресса; а₁, a₂ –коэффициенты эластичности по капиталу и труду.

Таким образом, мультипликативная ПФ обладает свойством 1, адекватным реальной экономике: при отсутствии одного из ресурсов производство не­возможно. Частным случаем этой функции служит функция Кобба-Дугласа

, где a₁=a, a₂=1– a.

Мультипликативная ПФ определяется по временному ряду выпусков и затрат ресурсов (Х_t, К_t, L_t,), t= 1, . Т, где T – длина временного ряда, при этом предполагается, что имеет место Т соотношений

,

где d_t — корректировочный случайный коэффициент, который приво­дит в соответствие фактический и расчетный выпуск и отражает флюк­туацию результата под воздействием других факторов, Мd_t = 1. Поскольку в логарифмах эта функция линейна:

получаем модель линейной множественной регрессии. Параметры функ­ции А, a₁, a₂ определяются методами корреляционно-регрессионного анализа, рассматриваемого в дисциплине «Эконометрика».

В качестве примера приведем мультипликативную функцию валово­го выпуска Российской Федерации (млрд. руб.) в зависимости от стои­мости основных производственных фондов (млрд. руб.) и числа занятых в народном хозяйстве (млн. чел.) по данным за 1960-1994 гг. (все стои­мостные показатели даны в сопоставимых ценах для этого периода):

X=0,931K 0,539 L 0,594

Мультипликативная функция обладает также свойством 2, адекватным реальной экономике: с ростом затрат ресурсов выпуск увели­чивается, т.е.

,

,

Частные производные выпуска по факторам называются предельными продуктами или предельными (маржинальными) эффективностямифакторов и представляют собой прирост выпуска на малую единицу прироста фактора:

– предельный продукт фондов, предельная фондоотдача (предельная эффективность фондов);

– предельный продукт труда, предельная производительность (предельная эффективность труда).

Для мультипликативной функции вытекает, что предельная фондоотдача пропорциональна средней фондоотдаче с коэффициентом a₁ , а предельная производительность труда – средней производительности труда с коэффициентом а₂:

, .

Из чего вытекает, что при а₁ 0,539 L 0,594 при увеличении основных фон­дов (ОФ) на 1% валовой выпуск повысится на 0,539%, а при увеличе­нии занятых на 1% – на 0,594%.

Если а₁ >a₂ имеет место трудосберегающий (интенсивный) рост, в противном случае – фондосберегающчй (экстенсивный) рост.

Рассмотрим темп роста выпуска

.

Если возвести обе части уравнения в степень , получим соотношение

,

в котором справа – взвешенное среднее геометрическое темпов роста затрат ресурсов, при этом в качестве весов выступают относительные эластичности факторов

, .

При а₁+ а₂ > 1 выпуск растет быстрее, чем в среднем растут факторы, а при а₁+ а₂ K_t, L_t+1>L_t) то согласно растет и выпуск (т.е. X_t+1>X_t),следовательно, при а₁+ а₂ > 1

,

т.е. действительно, темп роста выпуска больше среднего темпа роста факторов. Таким образом, при а₁+ а₂ >1 ПФ описывает растущую экономику.

Линией уровня на плоскости К, L, илиизоквантой, называется множество тех точек плоскости, для которых F(K, L)=Х₀=const. Для мультипликативной ПФ изокванта имеет вид:

или ,

т.е. является степенной гиперболой, асимптотами которой служат оси координат.

Для разных К, L, лежащих на конкретной изокванте, выпуск равен одному и тому же значению X₀, что эквивалентно утверждению о взаимозаменяемости ресурсов.

Поскольку на изокванте F(K, L) = Х₀ = const, то

.

В этом соотношении , , поэтому dK и dL имеют разные знаки: если dL 0, т.е. выбывший в объеме труд замещается фондами в объеме dK.

Поэтому естественно следующее определение, вытекающее из .

Предельной нормой замены S_K труда фондами называется отношение модулей дифференциалов ОФ и труда:

,

соответственно,предельная норма замены S_L фондов трудом

, при этом S_k S_L=1.

Для мультипликативной функции норма замещения труда фондами пропорциональна фондовооруженности:

, ,

что совершенно естественно: недостаток труда можно компенсировать его лучшей фондовооруженностью.

Изоклиналями называются линии наибольшего роста ПФ. Изокли­нали ортогональны линиям нулевого роста, т.е. изоквантам. Поскольку направление наибольшего роста в каждой точке (К, L) задается градиентом

grad , то уравнение изоклинали записывается в форме .

В частности, для мультипликативной ПФ получаем,

,

поэтому изоклиналь задается дифференциальным уравнением

,которое имеет решение

, ,

где (L₀; К₀) – координаты точки, через которую проходит изоклиналь. Наиболее простая изоклиналь при а = 0 представляет собой прямую

.

На рис. 1.1.4 изображены изокванты и изоклинали мультипликатив­ной ПФ.

При изучении факторов роста экономики выделяют экстенсивные факторы роста (за счет увеличения затрат ресурсов, т.е. увеличения масштаба производства) и интенсивные факторы роста (за счет повы­шения эффективности использования ресурсов).

Возникает вопрос: как с помощью ПФ выразитьмасштаб и эффективность производства? Это сравнительно легко сделать, если выпуск и затраты выражены в соизмеримых единицах, например представлены в соизмеримой стоимостной форме. Однако проблема соизмерения на­стоящего и прошлого труда до сих пор не решена удовлетворительным образом. Поэтому воспользуемся переходом к относительным (безраз­мерным) показателям. В относительных показателях мультипликативная ПФ записывается следующим образом:

,

т.е. X₀, K₀ L₀ — значения выпуска и затрат фондов и труда в базовый год.

Безразмерная форма, указанная выше, легко приводится к первоначальному виду

.

Таким образом, коэффициент получает естественную интерпретацию – это коэффициент, который соизмеряет ресурсы с выпуском. Если обозначить выпуск и ресурсы в относительных (безразмер­ных) единицах измерения через x, k, l, то ПФ в форме

.

Найдем теперь эффективность экономики, представленной ПФ. Напомним, что эффективность – это отношение результата к затратам. В нашем случае два вида затрат: затраты прошлого труда в виде фондов k и настоящего труда l. Поэтому имеются два частных показателя эффективности: – фондоотдача, – производительность труда.

Поскольку частные показатели эффективности имеют одинаковую размерность (точнее, одинаково безразмерны), то можно находить любые средние из них. Так как ПФ выражена в мультипликативной форме, то и среднее естественно взять в такой же форме, т.е. среднегеометриче­ское значение.

Итак, обобщенный показатель экономической эффективности есть взвешенное среднее геометрическое частных показателей экономичес­кой эффективности:

,

в котором роль весов выполняют относительные эластичности , , т.е. частные эффективности участвуют в образовании обобщенной эффективности с такими же приоритетами, с какими входят в ПФ соответствующие ресурсы.

Из вытекает, что с помощью коэффициента экономичес­кой эффективности ПФ преобразуется в форму, внешне совпадающую с функцией Кобба-Дугласа:

где Е – не постоянный коэффициент, а функ­ция от (К, L).

Поскольку масштаб производства М проявляется в объеме затрачен­ных ресурсов, то по тем же соображениям, которые были приведены при расчете обобщенного показателя экономической эффективности, сред­ний размер использованных ресурсов (т.е. масштаб производства)

В результате получаем, что выпуск Х есть произведение экономической эффективности и масштаба производства:

Линейная производственная функция

где E_K и E_L частные эффективности ресурсов.

E_K = – фондоотдача , E_L = – производитель труда.

Поскольку частные показатели эффективности имеют одинаковую размерность (точнее, одинаково безразмерны), то можно находить любые средние из них.

Пример 1.1.5. Валовой внутренний продукт США (Х), измеренный в млрд. долл. в ценах 1987г. возрос с 1960 по 1995 г. в 2,82 раза, основные производственные фонды за этот же период (К) увеличились в 2,88 раза, число занятых (L) – в 1,93 раза. Пусть X=2,248K 0,404 L 0,803 . Необходимо рассчитать масштаб и эффективность производства.

Сначала находим относительные эластичности по фондам и труду

.

Затем определяем частные эффективности ресурсов

,

,

после чего находим обобщенный показатель эффективности как среднее геометрическое частных:

.

Масштаб устанавливаем как среднее геометрическое темпов роста ресурсов

.

Таким образом, общий рост ВВП с 1960 по 1995 г. в 2,82 раза произошел за счет роста масштаба производства в 2,207 раза и за счет повыше­нии эффективности производства в 1,278 раза (2,82=1,278*2,207).

Приведем несколько типов производственных функций общего вида, наиболее часто используемых в экономической теории. Здесь x₁, x₂, … , x_n – значения факторов, определяющих производственную деятельность предприятия.

Функция Кобба-Дугласа. Функция вида:

.

Обычно считается, что сумма a_i равна 1.

Функция с постоянной эластичностью замещения. Удобная для анализа производственная функция:

,

где a именуется коэффициентом шкалы; b – коэффициентом замещения, u≤ 1 – коэффициент замещения; w – степень однородности.

Функция Леонтьева. Данная функция носит теоретический характер и описывает совершенно не гибкую технологию производства с очень большим количеством факторов, которые не могут заменить друг друга.

Обобщенная функция Леонтьева (функция с фиксированными пропорциями). В функцию Леонтьева просто вводится степень однородности:

.

Линейная производственная функция. Эта функция также является теоретической абстракцией. Уже по названию функции ясно, что:

Кусочно-линейная функция. Данная функция возникает как комбинация нескольких линейных производственных функций (т.е. технологий производства), каждая из которых используется на своем интервале. И для каждой комбинации факторов производства фирма выбирает ту технологию, которая дает наибольший выпуск:

.

Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право.

ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между.

Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам.

Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Функция полезности в уравнении слуцкого

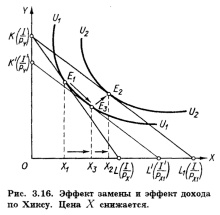
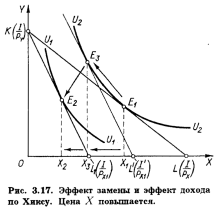
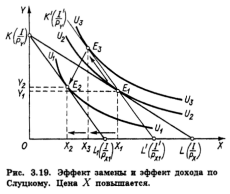
Существуют, однако, два подхода к определению реального дохода, связанные с именами английского экономиста Дж. Хикса и русского математика и экономиста Е. Е.Слуцкого. 1 Согласно Хиксу, разные уровни денежного дохода, обеспечивающие один и тот же уровень удовлетворения, т.е. позволяющие достигнуть одной и той же кривой безразличия, представляют одинаковый уровень реального дохода. Согласно Слуцкому, лишь тот уровень денежного дохода, который достаточен для приобретения одного и того же набора или комбинации товаров, обеспечивает и неизменный уровень реального дохода. Подход Хикса в большей мере соответствует основным положениям порядковой теории полезности, тогда как подход Слуцкого имеет то преимущество, что позволяет дать количественное решение задачи на основе статистических материалов. Сначала мы рассмотрим версию, предложенную Хиксом, как более общую. Затем покажем особенности решения, предложенного Слуцким.

Поэтому, как правило, кривые спроса на такие товары имеют обычно отрицательный наклон, как и в случае нормальных товаров. Лишь если положительный эффект дохода перекрывает отрицательный эффект замены, закон спроса нарушается ≈ его объем изменяется в том же направлении, что и цена. На рис. 3.18,6, например, (Х₃ — Х₂) > (Х₁ — Х₃). Такие товары называются товарами Гиффена. В действительности потребление большинства товаров требует лишь небольшой части средств потребителя и эффект дохода обычно невелик. Даже если он отрицателен, его размеры недостаточны для того, чтобы перекрыть влияние эффекта замены. Поэтому появление товаров Гиффена маловероятно.

Сравнив два подхода, мы видим, что метод Хикса предполагает знание потребительских предпочтений, кривых безразличия, тогда как метод Слуцкого не требует этого, он базируется на наблюдаемых и регистрируемых фактах поведения потребителя на рынке.