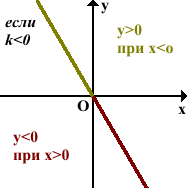Функция прямая пропорциональность уравнение функции

Функция прямая пропорциональность

Функция вида y=kx, где k — число (k≠0), называется функцией прямой пропорциональности (или функция прямая пропорциональность).

Число k называется коэффициентом пропорциональности. О переменной y говорят, что она пропорциональна переменной x.

Прямая пропорциональность — частный случай линейной функции y=kx+b (при b=0).

Графиком прямой пропорциональности является прямая, проходящая через начало координат — точку O (0;0).

Для построения графика прямой пропорциональности достаточно взять одну точку, вторая — точка O.

Свойства функции прямой пропорциональности

1) Область определения — множество действительных чисел:

2) Область значений — множество действительных чисел:

3) Нуль функции (y=0) при x=0.

4) При k>0 функция y=kx возрастает, при k 0 график функции проходит через I и III координатные четверти.

Функция принимает положительные значения при положительных значениях аргумента:

Функция принимает отрицательные значения при отрицательных значениях аргумента:

Число k называется угловым коэффициентом прямой y=kx.

k=tg α, где α — угол, который прямая образует с положительным направлением оси Ox.

Чтобы сравнить угловые коэффициенты прямых, сравниваем углы между прямыми и положительным направлением оси абсцисс.

Линейная функция. Прямая пропорциональность

Содержание

Из прошлого урока вы узнали многое о функциях, но далеко не все. Вспомним основные знания, которые нам будут нужны для понимания линейной функции:

• функция – это зависимость между двумя величинами, при которой каждому значению независимой переменной $x$ соответствует одно единственное значение другой зависимой переменной $y$;
• зависимость может быть прямой и обратной
• любая функция имеет область определения и область значений;
• графически функция может убывать и/или возрастать, может выглядеть как прямой, так и кривой линией.

Вот о функциях, график которых выглядит как прямая линия, и пойдет речь в данном уроке.

Примеры линейных функций

Представим ситуацию: в копилке лежит $500$ рублей, мама дает дочке каждый день на обеды и другие мелкие расходы $100$ рублей, но она тратит только $50$, а $50$ рублей кладет в копилку. Таким образом, через $10$ дней в копилке девочки будет уже на $500$ рублей больше: $50\times 10$. Всего же в копилке через $10$ дней будет $1000$ рублей: $500$ рублей накоплено за эти $10$ дней и $500$ рублей уже было.

Посмотрим, сколько же будет в копилке через $20$ дней: $ <50\times 20>+ 500 = 1500$ рублей.

Возьмем за функцию (зависимую переменную $y$) общее количество денег в копилке. Число дней, когда откладывались деньги, обозначим за $x$ (независимая переменная). Тогда наша функция (зависимость количества денег в копилке от количества прошедших дней) будет выглядеть в виде формулы: $y = <50\times x>+ 500$.

Посмотрим, как будет выглядеть график нашей функции. Для этого найдем несколько значений $y$ и заполним таблицу для $x$, например, равных $4$, $5$, $6$, $7$ (дней):

Найдем $y_1 = <50\times 4>+ 500 = 700$

Тогда $y_2 = <50\times 5>+ 500 = 750$

По точкам с координатами $(4, 700)$; $(5, 750)$; $(6, 800)$ и $(7, 850)$ построим график:

Как видим, график функции $y = <50\times x>+ 500$ выглядит как прямая линия.

Таким образом, увеличение денег в копилке будет напрямую зависеть от количества дней, в которые она пополнялась на одну и ту же сумму. При этом, зависимая переменная $y$ меняется на одну и ту же величину (в нашем случае ежедневное приращение суммы равно $50$ рублям).

Другой пример. Летом отключили горячую воду. Водонагреватель сломался, а помыться нужно. В ванну сначала налили два ведра кипятка, каждое по $10$ литров. Затем в нее пустили холодную воду из крана. В течение каждой минуты в ванну добавлялось еще 5 литров воды. Зависимость количества воды в ванной в нашем случае можно выразить с помощью формулы $y = <5\times x>+ 20$, где $y$ – количество воды в ванной, а $x$ – время в минутах, которое прошло с момента включения крана.

Что такое линейная функция

Итак, зависимость, подобная нашим примерам выше, функцию которой можно найти с помощью формулы вида $y = kx + b$, и называется линейной.

В данной формуле $k$ и $b$ – некоторые числа, называемые коэффициентами.

В наших случаях коэффициент $k$ был равен $50$ в примере с копилкой и $5$ в примере с ванной. Коэффициент $b$ в описанных примерах был равен $500$ рублям, уже лежавшим в копилке, и $20$ литрам, налитым в ванну до включения крана.

Если функцию можно задать формулой вида $y = kx + b$, где $k$ и $b$ – некоторые числа, а $x$ – независимая переменная, то ее называют линейной

Числовые коэффициенты $k$ и $b$ могут быть любыми числами: дробными и даже отрицательными.

Прямая пропорциональность и другие особые случаи

Давайте посмотрим, какие функции также будут линейными:

• $y = -3\times x- b$, в данном случае оба числовых коэффициента имеют отрицательные значения;
• другой пример: $y = 2-x$, здесь коэффициент $k$ равен $-1$, а $b = 2$;
• $y = 5$, тут коэффициент $k$ равен $0$, а коэффициент $b=5$ (в подобных случаях функция совсем не зависит от значения аргумента $x$, а лишь от числовой величины коэффициента $b$);
• а в функции $y = 4\times x$ коэффициент $b$ уже равен $0$.

Последний пример линейной функции (когда коэффициент $b$ равен $0$) – вариант прямой пропорциональности. Ранее вы уже изучали прямую зависимость. Такая зависимость – частный случай линейной функции, при котором формула будет выглядеть, как $y = kx$.

Вспомнить, что такое прямая зависимость

Если при увеличении одной величины, увеличивается другая, то величины называют прямо пропорциональными, у них прямая зависимость.

Чем больше денег — тем больше можно купить мороженого

Вернемся снова к нашим примерам: если бы в копилке и в ванной изначально было пусто, то функция $y$ увеличивалась бы прямо пропорционально увеличению количества потраченного на наполнение копилки или ванны времени. Коэффициент $b$ в таких случаях равен нулю.

Обратите внимание, что в формуле прямо пропорциональной функции коэффициент $b = 0$, но коэффициент $k$ не равен нулю.

Прямая пропорциональность y = kx и её график

Определение прямой пропорциональности

Если машина движется со скоростью 50 км/ч, пройденное расстояние (в километрах) в зависимости от времени (в часах) s = 50t. Время мы определяем как $t\geq0$. Но механика позволяет нам рассчитать не только будущее положение тела, но и прошлое, подставив в формулу $t \lt 0$ и запросто «прокрутив» время назад. Поэтому в общем случае, если движение было и остаётся постоянным, мы получаем:

Можно представить себе не только отрицательное время («поход в прошлое»). Ещё проще ввести отрицательные координаты: направо идём – координата растёт, становится положительной, поворачиваем налево – уменьшается, становится отрицательной.

В задачах, связанных с экономикой, величины также могут уходить в «плюс» и «минус»: покупки/продажи, кредиты/депозиты, доходы/затраты, прибыли/убытки . Часто эти величины изменяются на какую-то постоянную сумму с течением времени.

Если обобщить формулы, описывающие подобные зависимости, то получаем:

$$<\left\< \begin— \infty \lt x \lt + \infty — аргумент, \quad любое \quad действительное \quad число \\ k = const ≠ 0 \quad — параметр, \quad константа \\ y = kx \quad — функция\end \right.>$$

Функция такого вида называется прямой пропорциональностью .

Если $k \gt 0$, то чем больше x, тем больше y – функция возрастает.

Если $k \lt 0$, то чем больше x, тем больше y – функция убывает.

График прямой пропорциональности

Графиком прямой пропорциональности является прямая, проходящая через начало координат.

Согласно аксиоме планиметрии, через любые две точки можно провести прямую и притом только одну. Значит, положение прямой на плоскости полностью определяется двумя точками . Получаем:

Алгоритм построения графика прямой пропорциональности

• Выбрать произвольное значение аргумента $x_*\neq 0$
• Вычислить соответствующее значение функции $y_*=kx_*$
• Отметить на координатной плоскости точку $(x_*,y_* )$
• Провести прямую через начало координат (0;0) и точку $(x_*,y_* )$

Эта прямая – график прямой пропорциональности y=kx.