Функция решения двухмерного нестационарного уравнения теплопроводности

Решение двумерного уравнения теплопроводности. Черногорский Вячеслав. 6 курс

Содержание

Цель [ править ]

Численное решение уравнения теплопроводности в единичном квадрате с помощью функций библиотеки MPI.

Постановка задачи [ править ]

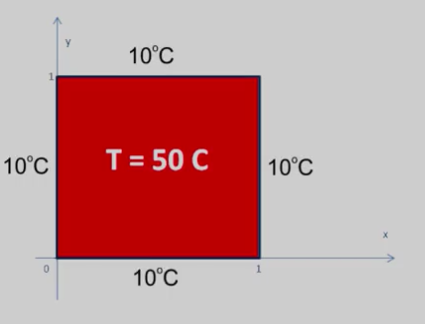
Имеется пластина в форме квадрата с ребром единичной длины. Пусть пластина разогрета до температуры Т_нач., и затем помещена в среду, которая имеет отличную температуру Т_среды. В этой задаче нас интересует процесс численного решения уравнения теплопроводности для пластины, которое выглядит следующим образом:

С граничными условиями

И начальным распределением температуры

[math]T(x,y,t) = 50 [/math]

Конечно-разностная схема [ править ]

Задача содержит производную по времени первого порядка и производные по пространственным координатам второго порядка. Запишем конечно-разностные аналоги слагаемых, входящих в уравнение

Методы решения УЧП

МЕТОДЫ РЕШЕНИЯ УЧП

1. Уравнение теплопроводности

Рассмотрим численное решение уравнений с частными производными (УЧП) на примере решения уравнения теплопроводности (диффузии)

— плотность тепловых источников, — коэффициент теплопроводности

Если , то мы имеем стационарное уравнение теплопроводности

— уравнение Пуассона.

Если плотность тепловых источников тоже равна 0, то получаемое уравнение называется уравнением Лапласа.

Стационарное уравнение теплопроводности может быть решено, если известны граничные условия.

Это могут быть или значения искомой функции на границе (задача Дирихле).

Или значения потока тепла на границе (задача Неймана)

Либо смешанные условия.

Если необходимо решать УЧП в области, имеющей круговую симметрию, оператор Лапласа удобна записать в полярных координатах:

2. РЕШЕНИЕ СТАЦИОНАРНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ

Будем решать задачу Дирихле для уравнения Пуассона.

в прямоугольной области , .

Для численного решения данной задачи применим метод SOR (метод последовательной верхней релаксации). Вначале используем метод конечных разностей. Для этого разобьем отрезок [a, b] на K равных интервалов длиной , а отрезок [c, d] — на L интервалов той же длины. Пусть при этом , . Тогда

Таким образом, мы разбили весь прямоугольник , на квадраты со стороной ,получив при этом сетку (решетку). Будем искать нужную нам функцию в узлах этой решетки методом конечных разностей. То есть будем искать эту функцию в виде матрицы

Запишем вначале в одномерном случае рамках метода конечных разностей производную функции U по х в точке . Получим

Для второй производной в точке получим

Аналогичным образом, для второй производной в точке имеем

Перейдем теперь к двумерной области и найдем вторые производные в точке , .

,

Подставив полученные таким образом вторые производные в уравнение Пуассона, имеем

Коэффициенты перед матричными элементами в данном случае равны 1 и 4. Однако в общем случае (полярные координаты, например) мы должны записать

и вычислить A, B, C, D, E.

Перепишем полученное нами уравнение в следующем виде:

Разность между левой и правой частями уравнения называется невязкой

Подставляя в правую часть (3) уравнение (1) имеем

Уравнение (4) является тождеством. Его можно использовать в случае, когда решение ищется методом последовательных приближений

Это и есть основное уравнение метода SOR. Параметр обычно выбирается не тождественно равным 1, изменяющимся параметром от 1 до 1.5. Это делается для лучшей сходимости метода. В качестве начального приближения берется функция, тождественно равная 0 внутри области определения и равная граничным условиям на границе области.

3. РЕШЕНИЕ НЕСТАЦИОНАРНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ

Будем искать решение этой задачи методом Кранка-Николсона. Рассмотрим вначале одномерное нестационарное уравнение диффузии.

Запишем производную по времени в k-й точке х в n-й момент времени в виде:

Здесь — шаг по времени. В правой части вторую производную по координате можно взять как в момент времени ,

так и в момент времени

Суть метода Кранка-Николсона заключается в том, что производная в правой части берется как среднее арифметическое от производных в точках и . То есть

Для двумерного уравнения диффузии

в рамках метода Кранка-Николсона запишем вторые производные по х и по у

как среднее арифметическое от производных в точках и ,

перенесем все значения функции в момент времени влево, а в — й вправо. Получим.

,

(1)

(2)

Схема расчета по методу Кранка-Николсона такова:

1. В начальный момент времени из начальных и граничных условий методом SOR (или каким-либо другим методом) находим значения функции U.

2. Вычисляем с ее помощью в этот же момент времени по формуле (2) функцию F.

3. По формуле (1) с помощью уже вычисленной функции F и граничных условий находим значение функции U в следующий момент времени.

4. Вычисляем с ее помощью по формуле (2) функцию F.

5. По формуле (1) находим значение функции U в следующий момент времени.

МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ

4. Решение одномерного уравнения теплопроводности

Базисные функции метода конечных элементов

Суть метода в том, что искомая функция ищется интерполяцией с помощью базисных функций. В этом случае отпадает необходимость расчета производных методом конечных разностей.

Пусть отрезок [a, b], на котором определяется искомая функция, разбит N точками на (N-1) равных отрезков (конечных элементов) длиной . На рисунке показан случай, когда N = 4.

Значения функции в этих точках равны , , . , . на каждом из конечных элементов функцию u(x) можно представить с помощью базисных функций :

Решение задач нестационарной теплопроводности.

НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ.

Общие положения. Описание процесса.

Ранее были рассмотрены условия распространения теплоты при стационарном режиме, когда температурное поле не менялось во времени, оставалось постоянным.

Если же температурное поле меняется во времени, т.е. является функцией времени, то протекающие в таких условия процессы называются нестационарными.

Нестационарные процессы теплопроводности встречаются при охлаждении и нагреве металлических заготовок, прокалывании твердых тел, в производстве стекла, обжига кирпича и т.д.

В качестве примера рассмотрим такой случай. Тело внесено в среду более высокой температурой; сразу же между средой и телом возникает процесс теплообмена, и тело начинает прогреваться. Сначала нагреваются поверхностные слои, но постепенно процесс прогрева распространяется вглубь тела (рис. 1.6.1).

По истечении некоторого времени (теоретически бесконечно большого) температура всех частей тела выравнивается и становится равной температуре окружающей среды, т.е. наступает тепловое равновесие.

На рис. 1.6.1 показан характер кривых, полученных при нагревании однородного твердого тела в среде с постоянной температурой .По мере нагрева температура в каждой точке асимптотически приближа­ется к температуре нагревающей среды. Наиболее быстро изменяется температура точек, лежащих вблизи поверхности тела. С увеличением времени прогрева эта разность будет уменьшаться и теоретически через достаточно большой отрезок времени она будет равна нулю.

При нестационарном режиме количество переданной теплоты также непостоянно во времени (рис. 1.6.2). По мере прогрева тела количество воспринимаемой теплоты уменьшается и в пределе становится равным нулю. Площадь, заключенная между осями и кривой, определяет собой полное количество теплоты, переданное за время . Эта теплота аккумулируется телом. Нестационарные тепловые процессы всегда связаны с изменением внутренней энергии или энтальпии вещества.

Аналогичным образом протекает и процесс охлаждения тела, при этом выделенная теплота передается в окружающую среду.

Скорость теплового процесса при нестационарном режиме определяется значением коэффициента температуропроводности

а , .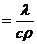

Любой процесс нагревания или охлаждения тела можно разделить на три режима.

Первый режим — начало процесса.

Характерной особенностью этого режима является распространение температурных возмущений в пространстве и захват все новых и новых слоев тела. Скорость изменения температуры в отдельных точках при этом режиме различна и зависит от начальных условий.

Это режим неупорядоченного процесса.

С течением времени скорость изменения температуры во всех точках тела становится постоянной. Это режим упорядоченного процесса, он называется регулярным режимом.

По прошествии длительного времени наступает третий режим, характерной особенностью которого является постоянство распределения температур во времени – это стационарный режим.

Например, в работе паровых котлов нестационарный режим возникает лишь при пуске в работу, выключении и изменении режима работы и имеет временный характер. Поэтому расчет таких аппаратов производится лишь для основного, стационарного режима, а для нестационарного совсем не рассчитывается. В работе же нагревательных печей, наоборот, нестационарный режим является основным, при их расчете приходится определять время, необходимое для прогрева металла до заданной температуры, или температуру, до которой металл нагреется в течение определенного промежутка времени.

Описанный характер изменения температуры и количества переданной теплоты справедливы лишь для твердых тел.

Решение задач нестационарной теплопроводности.

Решить задачу нестационарной теплопроводности это значит найти зависимость изменения температуры и количество теплоты переданной телу во времени для любой точки тела:

Для аналитического нахождения этих зависимостей может быть использовано дифференциальное уравнение теплопроводности Фурье:

.

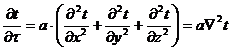
Это уравнение решается с помощью рядов Фурье. Аналитическое решение получается очень сложным и возможно лишь для тел простой формы (пластины, цилиндра и шара) при целом ряде упрощающих предпосылок.

Аналитическое описание процесса теплопроводности кроме дифференциального уравнения также включает в себя и условия однозначности.

Условия однозначности задаются в виде:

· физических параметров , , ;

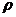
· формы и геометрических размеров объекта ;

· температуры тела в начальный момент времени 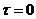; t = t₀ = f(x, у, z).

· граничных условий, которые могут быть заданы в виде граничных условий третьего рода:

.

Дифференциальное уравнение теплопроводности совместно с условиями однозначности дает законченную математическую формулировку рассматриваемой задачи. Решение ее заключается в отыскании функции, которая удовлетворяла бы уравнению и условиям однозначности.

t=f(x,y,z,i,a,t₀,t_ж, )

Если решить это уравнение для плоской стенки и рассмотреть процесс изменения температуры только в одном направлении x, то решение будет иметь следующий вид:

,

где b иcопределяются из условий стационарности процесса, т.е. при ;

, — из граничных условий 3 рода;

— из начальных условий, т.е. при .

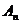
Из уравнения видно, что искомая функция t зависит от большого числа переменных, которые можно сгруппировать в 3 безразмерных комплекса, эти комплексы называются числами подобия.

Первое число подобия — Число Био:

,

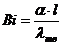
где — коэффициент теплоотдачи на границе жидкости и твердого тела;

λ — коэффициент теплопроводности твердого тела;

l— характеристический размер, который определяется в зависимости от формы тела:

для пластины l=δ;

для цилиндра l= ;

для шара l= .

Второе число подобия — Число Фурье:

,

гдеa— коэффициент температуропроводности;

Число Фурье называют также безразмерным временем.

Третий безразмерный комплекс — безразмерная координата:

.

Установлено, что θ— безразмерная температура, является функцией чисел Био и Фурье, для фиксированных значений , т.е.

.

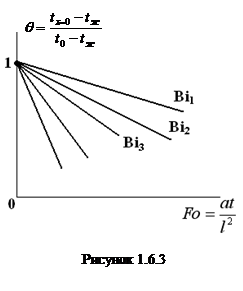
Изменение безразмерной температуры θ для центра ( 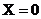) и поверхности ( ) можно представить графическим решением, которое приведено на рисунке 1.6.3.

Подобные графики построены для центра и поверхности пластины, цилиндра и шара, а так же для безразмерного количества теплоты, которая является функцией числа Bi и :

.

Следовательно, чтобы определить температуру на поверхности или в центре тела необходимо знать две величины: число Bi и число .

Таким образом, метод решения задач нестационарной теплопроводности заключается в следующем:

1) задаются геометрическими, начальными и граничными условиями [(с;λ; ; ;α; ),( или )];

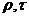
2) вычисляют числа Bi и ;

, ;

3) зная числа Bi и по графику, определяют безразмерную температуру θ;

4) определив θ, рассчитывают температуру в центре

или на поверхности тела

,

где — начальная температура тела;

— температура среды.

Рассмотрим влияние значений чисел Bi на распределение температуры в теле на примере охлаждения пластины.

Из полученного решения следует, что для любого момента времени температурное поле имеет вид симметричной кривой с максимумом на оси пластины ( ). В каждый последующий момент будет своя кривая, монотонно убывающая к поверхности (рис. 1.6.4).

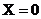
Для любого момента времени касательные к кривым в точках проходят через направляющие точки +А и

– А, которые расположены на расстоянии от поверхности пластины, причем

или ,

отсюда , т.е. расстояние до точки А полностью определяется условиями однозначности.

Сказанное справедливо для всех поверхностей.