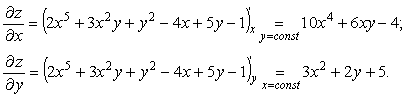Частные производные
Назначение сервиса . Сервис используется для нахождения частных производных функции (см. пример). Решение производится в онлайн режиме и оформляется в формате Word .
- Решение онлайн
- Видеоинструкция
- Также решают
Правила ввода функции, заданной в явном виде
- Примеры
x 2 +xy ≡ x^2+x*y .
cos 2 (2x+y) ≡ (cos(2*x+y))^2≡ (x-y)^(2/3)
Правила ввода функции, заданной в неявном виде
- Все переменные выражаются через x,y,z
- Примеры
≡ x^2/(z+y)
cos 2 (2x+zy) ≡ (cos(2*x+z*y))^2≡ z+(x-y)^(2/3)
Частные производные функции нескольких переменных
Пример 1 . z=2x 5 +3x 2 y+y 2 –4x+5y-1
Пример 2 . Найти частные производные 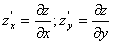
Находим частные производные:
Найдем частные производные в точке А(1;1)
Находим вторые частные производные:
Производная неявной функции онлайн
Неявная функция — это функция, например , заданная в виде уравнения:
F ( x , y ( x ) ) = 0
Как правило, вместо уравнения F ( x , y ( x ) ) = 0 пишут просто F ( x , y ) = 0 подразумевая, что есть функция от .
В качестве примера неявного задания функции, можно привести уравнение окружности:
уравнение декартового листа:
x 3 + y 3 = 3 ∙ a ∙ x ∙ y ( a = const ≠ 0 ) ,
и т.д. Все эти примеры можно записать в виде уравнения F ( x , y ) = 0 : уравнение окружности: F ( x , y ) = x 2 + y 2 − a 2 = 0 , уравнение декартового листа: F ( x , y ) = x 3 + y 3 − 3 ∙ a ∙ x ∙ y = 0 .
В связи с тем, что для исследования любой функции (в том числе и заданной неявно) необходимо вычислять производную, задача нахождения производной функции заданной неявно возникает довольно часто. Так, как же найти производную неявной функции? Исчерпывающий ответ на этот вопрос вы получите, воспользовавшись нашим онлайн калькулятором.
Для того, чтобы решить вашу задачу, для начала перепишите свою функцию в виде уравнения F ( x , y ) = 0 . Как это сделать, подробно описано выше (нужно просто перенести все слагаемые в левую часть уравнения, оставив справа ). Далее вам необходимо определиться, как у вас обозначается переменная и как обозначается функция, которая зависит от этой переменной. В приведенных выше примерах, — переменная, — функция, зависящая от .
Затем, вам необходимо ввести свое уравнение F ( x , y ) в наш онлайн калькулятор и получить решение вашей задачи.
Дифференцирование сложных и неявных функций


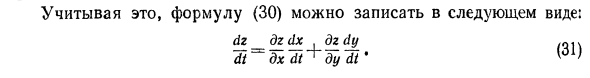





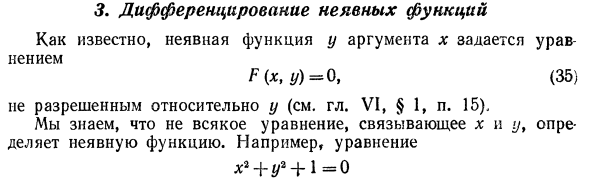

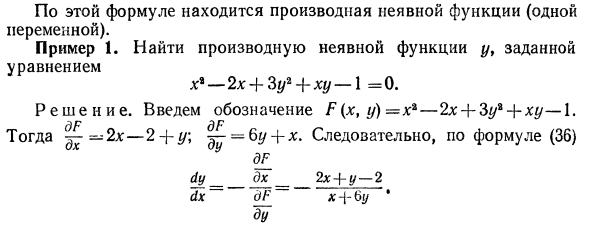
Дифференцирование сложных и неявных функций
- Отличие сложных функций от неявных функций 1. Дифференциация сложных функций Предположим, что z = f (x, y)> дано функции двух переменных, и аргумент этой функции является функцией одной независимой переменной t: x — x (t), y-. = Y (т). r — комплексная функция одной независимой переменной. Возникает проблема поиска производных Я знаю частные производные ^ и
для этой сложной функции ^ Производные ^ и
. При решении этой задачи функции x = x (t) и yy (t) имеют производные в точке t, а функция двух переменных z = f (xt y) дифференцируема в соответствующей точке y) Предположим, что есть.
Условия, которым должно удовлетворять уравнение F (x, y) = 0, Чтобы определить неявную функцию у? Ответ на этот вопрос дает следующая теорема. Теорема о неявной функции. Функция F (a \ y) и ее частные производные F’x (xt y) и F’y (xt y) определены непрерывно в окрестности точки P0 (x0 \ y0) и F (xot yo) = 0, F’y (x0, yQ) Φ0, уравнение F (x, /) = 0
Не определяет функцию y (означает только фактическое значение переменной). Людмила Фирмаль
Определите уникальную неявную функцию y = y (x) и y (x0) = y0, которая непрерывно дифференцируема в интервале, включая точку x0 вблизи точки P0 (x0; y9). Эта теорема оставлена без доказательства. Пусть левая часть уравнения (35) удовлетворяет условию, указанному в теореме. Затем уравнение определяет неявную функцию y — y (x), которая содержит тождество вблизи точки p0 (* 0; y0). F (xty (x)) * что O Относительно х.
Производная функции, равная нулю, также равна нулю, поэтому полная производная дР l = 0 дх Однако согласно уравнению (32) Так где d £ _dF dF_ dy dx dx dy dx * дх ду дх
1 дф DY _ DX дх дФ * (36) ду Это выражение находит производную (одну переменную) неявной функции. Пример 1. Найти производную неявной функции y, заданной уравнением 2x + 3y * + xy-1 = 0. Решения. Введено обозначение F (x, y) = x% —2x +% + xy— . дф ^ р Тогда —2x — 2 — \ — y \ = 6y — \ — x. Следовательно, формула (36) есть ди-джей dy_dx_2x + y-2 dx
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Особенно в точке P2 (2; -1) ду дх , * = 2 2-f 6 (–1) 4 ‘. ‘/ = -1 Пример 2. Нахождение уравнений для касательных и кривых нормалей * xby + etv ‘- y ^ O Точка P0 (0; 1). Решения. Функция F (x, y) = x2y-f * e2v2 — Найти первую частную производную от y и значение в точке P0 (0; 1). F’x (x, y) = 2hu + y * e * yy \ F’y (x, y) к x> + 2hue * «r-1; F’A0, 1) = 1; F’y (0; 1) = -1 Используйте уравнение (36) для расчета коэффициента тангенса угла к cas
dx ^ (0,1) -1 • Следующий коэффициент нормального угла / o P Разделив обе части равенства (29) на Dt и передав их до предела как At -► 0, получим: n £ * lim% + Hin lim * (30) d / ^ 0D / OX A / oD ‘dU A / -o L / D / — * 0L’
Переменные x и y получают приращения Ax и Du соответственно, а функция r получает приращение Ar. Людмила Фирмаль
Если каждый предел существует в правой части этого уравнения, то есть предел в левой части Производная этого уравнения, т. Е. Дифференциал Но
= и limτm = r dt d / -, oA ‘dt d / -> oL / dt Существует по предположению. Найду Lim Lim F-. ^ W Hm®. ободок Д / ОД / -. 0ХРЛ / / А / — »0 ПД / ^ 0Д / Рассмотрим сначала Ита лим-д / -> о д / — »» об А / Производные
и dt At- * o P как At-> 0, прежде чем найти предел И р—> 0 **. Но тогда liin- = lim- = 0, так д / -оРр-> оР
Учитывая это, уравнение (30) можно записать в следующем формате: dz_dzdx. dzdy Jt
yTf Пример 1. Найти производную ^, если 2 = xy, x = sint, y = tz. Решения. (> Применение Jurmula (31) Tt = W *% + WYvjt
yxy-1 (s \ nt) ‘+ xy \ nx (/ «)» = -yxy
l cos * + xY В x. 2t = t2 (sin «: 1 COS t -f -2 / (грех /) » 14— 1 + -1 год 8 ■ — £ ■■ 1 + 1 • f)> + * + — 1 х От X2 до ‘X2-я- * Y2 Теперь у нас есть 4- = 4-й + * да ‘да + х2 + т / 2 2 года Xg + y- Если вам нужно доказать. 2 (а-а) 2 (а-во) _ и-а
Инвариантность формы полной дифференциации Как известно, форма инвариантна для производной функции от одной переменной y / (x). Это потому, что дифференциальное уравнение dy = f ‘(x) dx Это остается верным независимо от того, является ли x независимой переменной или функцией переменной: x = μ (t) (см. Главу VI, § 3, пункт 4). Для функции с несколькими переменными u = f (x, y, r, …, f) выполняется аналогичное утверждение: n переменных uf (xt y, r, …, f) Полная производная функции сохраняет свою форму , Di. Ди ди, ди
l Независимо от того, являются ли *, y, z, …, t независимыми переменными или функциями других переменных. Ограничение доказательства этого утверждения только для функций с двумя переменными z = f (x, y). Как вы знаете, если x и y являются независимыми переменными, общая разница имеет вид dz = tdx +% dy- Указывает, что эта форма производной сохраняется, когда x и y становятся функциями новых переменных: u), y-y (u, u). В этом случае z является комплексной функцией от u и u.
Производная этой сложной функции дается dz = p-du +% dv. Ди 1 ди Однако согласно уравнениям (33) и (34) дг _ дг_ дх, дз до ди дх ди до * ди9 dg _ dg_ dh .dz do ди дх ди ‘до ди’ так , (Dz dx, dg dy . (Dg dx, dg dy \, dz = (Tx-Tu + ry-fu) du + (Tx-d-o + d-y-i) dv = j * d0 + *. ftdu + *. д’и .. дх ди 1 дх ди дю ди дю ду — £ (£ * + £ *) + t (a> + t>) = с того времени дг. DZ = didx + jydy> *
Du + ^ dv = dx, a ^ du — \ — ^ dv = dy Поэтому вся минута дз не меняет своей формы. дз, дз ты Когда x и y являются функциями других переменных
Неявное разграничение функций Как вы знаете, неявная функция аргумента x дается F (x, y) = 0, (35) Не допускается для y (см. Главу VI, § 1, стр. 15) Я знаю, что не все уравнения, связывающие x и y, определяют неявные функции. Например, уравнение х * + у2 + 1 = 0




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://mathforyou.net/online/calculus/derivative/implicit/
http://lfirmal.com/differencirovanie-slozhnyh-i-neyavnyh-funkcij/
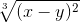 ≡ (x-y)^(2/3)
≡ (x-y)^(2/3)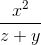 ≡ x^2/(z+y)
≡ x^2/(z+y) 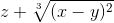 ≡ z+(x-y)^(2/3)
≡ z+(x-y)^(2/3)