Функции, заданные параметрически, и их дифференцирование






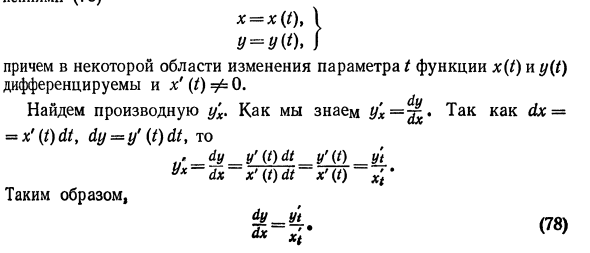


Функции, заданные параметрически, и их дифференцирование
- Функции, задаваемые параметрами и их отличиями /. Параметрические обязанности и линии До сих пор рассматривались линейные уравнения на плоскости, которые непосредственно связывают текущие координаты этих точек. Тем не менее, другой метод определения линий часто используется. В этом методе текущие координаты x и y считаются функцией третьей переменной. Укажите две функции переменной /. (73) То же значение / считается.
Когда переменная t проходит через все значения области функции (73), точка My) описывает конкретную линию C в плоскости Ohu. Уравнение (73) называется параметрическим уравнением этой линии, а переменная / называется параметром. Предположим, что функция x = x (() имеет обратную функцию / = φ (:) :).
Тогда одно из этих значений t соответствует однозначному значению x и однозначному значению y, так что определенная точка M (x \ y) соответствует. Людмила Фирмаль
Подставляя эту функцию во второе выражение (73), выражение (74) y = y [Φ (A ‘)], Выразите y как функцию от x. Я согласен, что эта функция параметрически определяется уравнением (73). Переход от этих уравнений к уравнению (74) называется исключением параметров. При рассмотрении функциональности, Найдите вторую производную. Второй по определению FX.
Dx2 рф * ‘дх Функция параметра- = / (/), DY \ дх) дх d ^
Следует рассматривать как заданную функцию Параметрический: 1 * = «(/). J ■ ‘8 Следовательно,
= определяется уравнением (78) вместо y ду Должен быть заменен (А ты (79) «» Dar Пример 3. Найти вторую производную функции y, определенной параметрически. x = sin2 /, ^ y = sin2 /. ) Решения. В примере 1 первая производная была найдена, но рассматривают эту производную как параметрически определенную функцию. | = 2ctg2 /, | я Пой- ^ 7.
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Согласно уравнению (78) * = найти sin2 /, вторая производная dyV ‘2 2 «в уравнении (79) Y /(2 ctg _ sin * 2 /__4dx2 «» * * (sin2 /) ‘
2 sin / cos / sin * 2 /’ \ Когда вы указываете параметр, исключение параметра не только не требуется, но и не всегда возможно на практике. Во многих случаях гораздо удобнее запрашивать разные значения для параметров и использовать уравнение (73) для вычисления соответствующих значений для аргументов x и y. Давайте посмотрим на некоторые примеры.
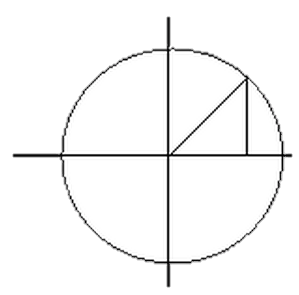
Пример 1.Декартовы координаты x и y этой точки выражаются полярным радиусом r-R и полярным углом. , §3, пункт 3): x = Rcostt \ y = Rs \ nt. ((7 ° Уравнение (75) называется параметрическим круговым уравнением. Эти параметры являются полярным углом / и варьируются от 0 до 2n. Если уравнение (75) возводится в квадрат и заканчивается для каждого члена, тождество устраняется тождеством cos2 // fsin2 / = 1, а круговое уравнение в декартовой системе координат xx + y2z = R * f определяет две основные функции вы: И tj- * / R2-A2’2. Каждая из этих функций определяется параметрически уравнением (75), но диапазон изменения параметров для этих функций различен.
Пусть M — любая точка на окружности с центром в начале координат и радиусе R. Людмила Фирмаль
Их первый 0 я Кроме того, в конкретной области изменения параметра t функции x (t) и y (t) дифференцируемы и x ‘(/) Φ0. Найдите производную y’x. Как вы знаете, yx = ^ 6 * dx = = x ‘(t) dt, dy = y’ (t) dt, то > dy_y ‘(t) dt y’ (t) yt yx dx x ‘ Пример 1. Найти производную функции y от k, заданную параметрическим уравнением x = sin2 /, \ y = sin2 /. Решение. Из уравнения (78) dy_y’t _ (sin 2Q ‘_ 2cos21 0 0 dx to x; (sin54 /)’ 2 sin / cos / ^ 8 Пример 2. Найти касательные и циклоидальные нормальные уравнения (А = 1) x = / -sin ^ r / = 1-cos / / T Y ‘решение в точке Ml (xr; yx), соответствующей значению параметра. Найти координаты контакта Mt (xx \ yv). т. , Зло зла зло. Зло | -2 *! = (/ -Sin /) / = zy = -2 — Sin-2- = -2- + 1 * зло yt = (\ -cos /) = 1 — COS— = 1. • г Найти производную от уравнения (78), чтобы найти коэффициенты тангенса и нормального угла. dy_ (1-cos /) ‘_ sin t dx Найти угловой коэффициент касательной к циклоиде в точке М. b-dJ-1- (sin / \ = —I * kas- Образовательный сайт для студентов и школьников Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника. © Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института Вы будете перенаправлены на Автор24 Пусть даны два уравнения $x=\phi (t)$ и $y=\psi (t)$ В которых $t$ принимает значения с отрезка [n1; n2]. Каждому значению t соответствуют значения x и y — координаты точки на плоскости Оxy. Когда $t$ изменяет свое значение на промежутке от $n1$ до $n2$, точка описывает некоторую кривую. Уравнения $x=\phi (t)$ и $y=\psi (t)$ получили название параметрических для кривой, а $t$ — параметра. Предположим, что функция $x=\phi (t)$ имеет обратную функцию $t=\ (x)$. Тогда справедливо равенство: Параметрический способ задания функций широко применяется в механике. Так, если в плоскости некоторая материальная точка находится в движении (время $t$), и законы движения проекций этой точки на оси координат известны: Уравнения являются параметрическими уравнениями траекторий движущейся точки. Исключая временной параметр, получим уравнение траектории в форме $y = f(x)$. Определить траекторию и место падения груза, сброшенного с самолета, движущегося горизонтально со скорость $v_0$ на высоте $y_0$. Допустим, что груз сбрасывается с момент пересечения самолетом оси Oy. Тогда очевидно, что горизонтальное перемещение груза равномерно и имеет постоянную скорость: А вертикальное перемещение: Следовательно, расстояние от груза до земли в произвольный момент падения: Уравнения горизонтального и вертикального перемещения тела являются параметрическими. Для того, чтобы исключить временной параметр $t$, найдем его значение из первого уравнения. Полученное выражение подставим во второе параметрическое уравнение чтобы найти уравнение траектории: Параметрические кривые окружности: Рисунок 1. Окружность и ее параметрические кривые Уравнение гиперболы имеет вид: Параметрические кривые гиперболы: Рисунок 2. Гипербола и ее параметрические кривые Записать уравнение окружности в параметрическом виде.



















































Параметрическое задание функции
Параметрический способ задания функций
Готовые работы на аналогичную тему
Уравнения некоторых кривых в параметрической форме:
Представим уравнение окружности в виде: \[x^ <2>+y^ <2>=r^ <2>\] \[x^ <2>+y^ <2>=6^ <2>\]
Значит, радиус $r$ равен 6.
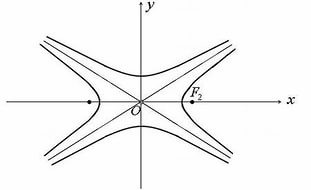
Записать уравнение гиперболы в параметрическом виде.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 11 12 2021
Производная параметрически заданной функции
| x = φ ( t ) , y = ψ ( t ) , t ∈ ( a ; b ) | |
| y x ‘ = ψ ‘ ( t ) φ ‘ ( t ) | y x » = ψ » ( t ) · φ ‘ ( t ) — ψ ‘ ( t ) · φ » ( t ) φ ‘ t 3 |
Функцию можно задать несколькими способами. Это зависит от правила, которое используется при ее задании. Явный вид задания функции имеет вид y = f ( x ) . Бывают случаи, когда ее описание невозможно или неудобно. Если есть множество пар ( х ; у ) ,которые необходимо вычислять для параметра t по промежутку ( а ; b ) . Для решения системы x = 3 · cos t y = 3 · sin t с 0 ≤ t 2 π необходимо задавать окружность с центром координат с радиусом равным 3 .
Определение параметрической функции
Отсюда имеем, что x = φ ( t ) , y = ψ ( t ) определены на при значении t ∈ ( a ; b ) и имеют обратную функцию t = Θ ( x ) для x = φ ( t ) , тогда идет речь о задании параметрического уравнения функции вида y = ψ ( Θ ( x ) ) .
Бывают случаи, когда для исследования функции требуется заниматься поиском производной по х . Рассмотрим формулу производной параметрически заданной функции вида y x ‘ = ψ ‘ ( t ) φ ‘ ( t ) , поговорим о производной 2 и n -ого порядка.
Вывод формулы производной параметрически заданной функции
Имеем, что x = φ ( t ) , y = ψ ( t ) , определенные и дифферецируемые при значении t ∈ a ; b , где x t ‘ = φ ‘ ( t ) ≠ 0 и x = φ ( t ) , тогда существует обратная функция вида t = Θ ( x ) .
Для начала следует переходить от параметрического задания к явному. Для этого нужно получить сложную функцию вида y = ψ ( t ) = ψ ( Θ ( x ) ) , где имеется аргумент x .
Исходя из правила нахождения производной сложной функции, получаем, что y ‘ x = ψ Θ ( x ) = ψ ‘ Θ x · Θ ‘ x .
Отсюда видно, что t = Θ ( x ) и x = φ ( t ) являются обратными функциями из формулы обратной функции Θ ‘ ( x ) = 1 φ ‘ ( t ) , тогда y ‘ x = ψ ‘ Θ ( x ) · Θ ‘ ( x ) = ψ ‘ ( t ) φ ‘ ( t ) .
Перейдем к рассмотрению решения нескольких примеров с использованием таблицы производных по правилу дифференцирования.
Найти производную для функции x = t 2 + 1 y = t .
Решение
По условию имеем, что φ ( t ) = t 2 + 1 , ψ ( t ) = t , отсюда получаем, что φ ‘ ( t ) = t 2 + 1 ‘ , ψ ‘ ( t ) = t ‘ = 1 . Необходимо использовать выведенную формулу и записать ответ в виде:
y ‘ x = ψ ‘ ( t ) φ ‘ ( t ) = 1 2 t
Ответ: y x ‘ = 1 2 t x = t 2 + 1 .
При работе с производной функции ч параметром t указывается выражение аргумента x через этот же параметр t , чтобы не потерять связь между значениями производной и параметрически заданной функции с аргументом, которому и соответствуют эти значения.
Чтобы определить производную второго порядка параметрически заданной функции, нужно использовать формулу производной первого порядка на полученной функции, тогда получаем, что
y » x = ψ ‘ ( t ) φ ‘ ( t ) ‘ φ ‘ ( t ) = ψ » ( t ) · φ ‘ ( t ) — ψ ‘ ( t ) · φ » ( t ) φ ‘ ( t ) 2 φ ‘ ( t ) = ψ » ( t ) · φ ‘ ( t ) — ψ ‘ ( t ) · φ » ( t ) φ ‘ ( t ) 3 .
Найти производные 2 и 2 порядка заданной функции x = cos ( 2 t ) y = t 2 .
Решение
По условию получаем, что φ ( t ) = cos ( 2 t ) , ψ ( t ) = t 2 .
Тогда после преобразования
φ ‘ ( t ) = cos ( 2 t ) ‘ = — sin ( 2 t ) · 2 t ‘ = — 2 sin ( 2 t ) ψ ( t ) = t 2 ‘ = 2 t
Отсюда следует, что y x ‘ = ψ ‘ ( t ) φ ‘ ( t ) = 2 t — 2 sin 2 t = — t sin ( 2 t ) .
Получим, что вид производной 1 порядка x = cos ( 2 t ) y x ‘ = — t sin ( 2 t ) .
Для решения нужно применить формулу производной второго порядка. Получаем выражение вида
y x » = — t sin ( 2 t ) φ ‘ t = — t ‘ · sin ( 2 t ) — t · ( sin ( 2 t ) ) ‘ sin 2 ( 2 t ) — 2 sin ( 2 t ) = = 1 · sin ( 2 t ) — t · cos ( 2 t ) · ( 2 t ) ‘ 2 sin 3 ( 2 t ) = sin ( 2 t ) — 2 t cos ( 2 t ) 2 sin 3 ( 2 t )
Тогда задание производной 2 порядка с помощью параметрической функции
x = cos ( 2 t ) y x » = sin ( 2 t ) — 2 t cos ( 2 t ) 2 sin 3 ( 2 t )
Аналогичное решение возможно решить другим методом. Тогда
φ ‘ t = ( cos ( 2 t ) ) ‘ = — sin ( 2 t ) · 2 t ‘ = — 2 sin ( 2 t ) ⇒ φ » t = — 2 sin ( 2 t ) ‘ = — 2 · sin ( 2 t ) ‘ = — 2 cos ( 2 t ) · ( 2 t ) ‘ = — 4 cos ( 2 t ) ψ ‘ ( t ) = ( t 2 ) ‘ = 2 t ⇒ ψ » ( t ) = ( 2 t ) ‘ = 2
Отсюда получаем, что
y » x = ψ » ( t ) · φ ‘ ( t ) — ψ ‘ ( t ) · φ » ( t ) φ ‘ ( t ) 3 = 2 · — 2 sin ( 2 t ) — 2 t · ( — 4 cos ( 2 t ) ) — 2 sin 2 t 3 = = sin ( 2 t ) — 2 t · cos ( 2 t ) 2 s i n 3 ( 2 t )
Ответ: y » x = sin ( 2 t ) — 2 t · cos ( 2 t ) 2 s i n 3 ( 2 t )
Аналогичным образом производится нахождение производных высших порядков с параметрически заданными функциями.
http://spravochnick.ru/matematika/proizvodnaya_i_differencial/parametricheskoe_zadanie_funkcii/
http://zaochnik.com/spravochnik/matematika/proizvodnye/proizvodnaja-parametricheski-zadannoj-funktsii/