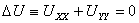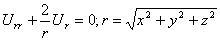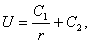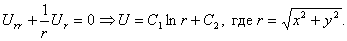Гармонической функцией называется решение уравнения

Лекция 7. Гармонические функции и их свойства

Рассмотрим уравнение Лапласа на плоскости

и в пространстве

Уравнение (33) при переходе к полярным координатам преобразуется к виду

Рис 14 Рис 14.1

Если в пространстве перейти к сферическим координатам

то уравнение (34) примет вид

Функции U=U(x,y) на плоскости и U=U(x,y,z) в пространстве, имеющие непрерывные частные производные второго порядка и удовлетворяющие, соответственно, уравнению Лапласа (33) или (34) в некоторой области D, называются гармоническими в этой области. Простейшими примерами гармонических функций являются линейные функции: U = ах + by + с на плоскости и U = ax + by + cz + d в пространстве. Особый интерес представляют решения уравнения Лапласа, обладающие сферической или цилиндрической (в случае двух независимых переменных — круговой) симметрией.

Решение U=U(r), обладающее сферической симметрией, будет определяться из обыкновенного дифференциального уравнения

Это уравнение получится, если подставить искомую функцию в уравнение Лапласа (34*), записанное в сферических координатах. Интегрируя это уравнение, находим

где C₁ и C₂ — произвольные постоянные. Полагая C₁=1, C₂=0, получим функцию

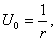
которую часто называют фундаментальным решением уравнения Лапласа в пространстве. Функция U₀ является гармонической всюду в пространстве, кроме начала координат 0.

Аналогично, полагая U=U(r) и пользуясь уравнением Лапласа в цилиндрических или полярных координатах, найдем решения, обладающие цилиндрической или круговой симметрией:

Выбирая С₁=-1 и С₂=0, будем иметь функцию

Рассмотрим в пространстве электрическое поле, образованное точечным зарядом величины q , помещенным в начало координат. Тогда потенциал этого поля равен

Аналогично, если рассмотреть поле, создаваемое заряженной прямой, то потенциал такого поля будет равен

где q₁ — линейная плотность заряда (то есть заряд, рассчитанный на единицу длины).

Более сложные примеры будут рассмотрены далее, а сейчас изучим свойства гармонических функций.

Теорема о среднем. Пусть функция U=U(x,y) гармоническая в некотором круге D радиуса R с центром (х_o,у_o) и непрерывная в соответствующем замкнутом круге Тогда значение этой функции в центре круга равно ее среднему значению на окружности Г, ограничивающей данный круг, то есть

При доказательстве этой теоремы применим интегральную формулу Пуассона для круга, которая будет доказана позже в лекции 10. Она имеет вид (см. рис. 15)

Если в этой формуле положить ρ=0, то получится формула (35).

Теорему о среднем можно представить и в другой форме. Для этого запишем формулу (35) для произвольного круга радиуса r, где 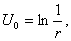(см. рис.15.1):

Умножив обе части равенства (36) на rdr и проинтегрировав по r в пределах от 0 до R, получим:

где D — круг радиуса R. Разделив обе части полученного равенства на R 2 /2 , будем иметь

В правой части формулы (37) записано среднее значение гармонической функции U(x,y) в круге радиуса R.

Имеет место и обратная теорема: если в некоторой области D функция U=U(x,y) непрерывная и для каждой точки выполняется теорема о среднем в любом сколь угодно малом круге с центром в точке (х_о, у_о), то эта функция гармоническая в D. Из формулы (37) получается:

Следствие. Если функция U=U(x,y) гармоническая в некотором круге D радиуса R и непрерывная в соответствующем замкнутом круге ,то

Число называют нормой функции U=U(x,y) в области D , и неравенство (38) можно переписать в виде

Неравенство (38) доказывается совсем просто, если воспользоваться известным неравенством Коши-Буняковского:

Применим это неравенство к формуле (37):

Что и требовалось доказать.

Гармонические функции, помимио вышеуказанных свойств, обладают и многими другими свойствами. Приведем еще два из них.

Неравенство Харнака. Пусть функция гармоническая в некотором круге D радиуса R c центром (x_o, у_o) и непрерывная в соответствующем круге Тогда при любом она удовлетворяет неравенству

Из неравенства Харнака следует теорема Лиувилля.

Теорема Лиувилля. Гармоническая на всей плоскости функция U=U(x, у) не может быть ограниченной сверху или снизу, если она не постоянная.

Доказательство. Если функция U=U(x, у) ограничена сверху, то U₁=-U(x, y) — ограничена снизу и тоже гармоническая. Поэтому достаточно рассмотреть случай, когда функция ограничена снизу: Более того, можно считать, что M=0. Действительно, ,а разность (U-M) тоже гармоническая функция. Итак, предполагая существование гармонической во всей плоскости неотрицательной функции U(x, у), мы докажем, что эта функция постоянная.

Воспользуемся неравенством Харнака

Если функция U(x, у) гармоническая во всей плоскости то, фиксировав произвольное и неограниченно увеличивая R мы получим

то есть Теорема Лиувилля доказана.

Замечание. Гармонические функции в пространстве обладают аналогичными свойсвами. Приведем формулировку одного из них.

Терема о среднем. Пусть функция U=U(x, у) гармоническая в некотором шаре D радиуса R c центром
(x_o , у_o , z_o ) и непрерывная в соответствующем замкнутом шаре Тогда значение этой функции в центре шара равно:

а) ее среднему значению на сфере Г, ограничивающей данный шар, то есть

б) ее среднему значению в шаре D, то есть

Электронная библиотека

Пусть имеем аналитическую в области D функцию . Тогда она удовлетворяет условиям Даламбера-Эйлера:

Дифференцируя (а) по х, а (б) по у и складывая, получим:

Дифференцируя (а) по у, а (б) по х и вычитая, будем иметь:

Равенства (2.36) и (2.37) говорят о том, что функции и , являющиеся соответственно действительной и мнимой частями аналитической функции в некоторой области , в той же области являются решениями уравнения Лапласа ( ).

Определение. Функция, являющаяся решением уравнения Лапласа, называется гармонической функцией.

Таким образом, мы доказали, что действительная и мнимая части аналитической функции являются гармоническими.

Это не значит, что если и есть произвольно выбранные гармонические функции, то – аналитическая, так как условия (2.31) не всегда будут выполняться.

Возникает задача построения аналитической функции по заданию одной из гармонических функций или .

Для решения задачи, задав, например, мнимую часть найдем, используя условия (2.31).

Две гармонические функции, удовлетворяющие условиям (2.31) и, следовательно, являющиеся действительной и мнимой частями некоторой аналитической функции называются сопряженной парой гармонических функций.

Отметим, что функция определяется с точностью до постоянного слагаемого. Для определения постоянной задают дополнительные условия в виде значения функции в фиксированной точке.

Построить аналитическую функцию , если известно, что ее действительная часть .

Решение. Проверим сначала, что гармоническая на всей плоскости функция:

Из условий (2.31) найдем гармонически сопряженную ей функцию :

Проинтегрируем первое уравнение по у, считая х постоянным, получим:

Используем второе условие:

откуда , где С – постоянная интегрирования.

По условию задачи , значит, С=1, и мы имеем:

Задачи для упражнений

1) Проверить, выполняются ли условия Даламбера-Эйлера, и, если они выполняются, найти производные функций: а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з) ; и) .

2) Найти аналитическую функцию , если:

(у = 0, х £ 0 – исключается из области).

плоскость с разрезом: вдоль полуоси

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Гармонической функцией называется решение уравнения

Интеграл Дирихле, первая, вторая и третья формулы Грина. Гармонические функции и их свойства, теоремы о гармонических функциях. Шаровые и сферические функции. Дифференциальное уравнение для сферических функций и его решение.

В данном разделе перечислим без вывода основные формулы теории потенциала, которые находят применение в теории фигуры Земли. Остановимся лишь на некоторых, наиболее важных теоремах.

Введем векторный оператор набла :

, где — единичные, взаимно ортогональные вектора. С векторным оператором можно обращаться, как с обыкновенным вектором. Например, скалярное произведение двух операторов набла дает оператор Лапласа: .

Допустим, что в нашем распоряжении имеется некоторая скалярная функция . Тогда

С помощью оператора Лапласа интегрирование по объему можно заменить интегрированием по поверхности. В дальнейшем для обозначения пределов интегрирования мы будем использовать следующий прием. Все двукратные или трехкратные интегралы мы будем изображать однократным интегралом. Под интегралом будем использовать символ ( ) если интегрирование ведется по телу, ограниченному поверхностью , или просто значком , если интегрирование ведется по поверхности . С этими где оговорками формула Остроградского (3.1) принимает вид

где — элемент объема, — элемент поверхности, а буквой обозначена внешняя нормаль.

3.1.2 Первая формула Грина

Введем обозначение оператора

тогда первая формула Грина примет вид

Интеграл по объему от функции называется интегралом Дирихле:

Очевидно, что в формуле Грина функции и можно менять местами, то есть вместо (3.3) можно написать

Вычитая левые и правые части формул (3.3) и (3.5), получим вторую формулу Грина

Рассмотрим частный случай, когда , где — расстояние между двумя точками P(x,y,z) и Первая точка имеет фиксированные координаты, а вторая — принадлежит телу и имеет текущие координаты, принадлежащие элементу объема. Тогда

Нетрудно убедиться, что для , имеет место равенство . Имеем

Проделаем следующие выкладки

Обратимся снова к второй формуле Грина. Перепишем ее для случая, когда . Возможны три варианта, когда точка лежит вне тела, внутри его и на поверхности, которое ограничивает это тело.

Точка Р — внешняя. В этом случае во всем внутреннем пространстве тела, по которому ведется интегрирование, радиус-вектор r не обращается в нуль и . Вторая формула Грина (3.6) принимает вид

Мы получили третью формулу Грина для внешней точки.

Точка Р — внутренняя. В одной точке внутреннего пространства радиус-вектор обращается в нуль и функция обращается в бесконечность. Опишем вокруг этой точки сферу с малым радиусом. Интегрирование по телу, ограниченному поверхностью , можно разбить на два этапа: интегрированию по всем точкам тела, исключая малую сферу, содержащую точку , и интегрирование по малому шару, ограниченному малой сферой :

где — тело с выколотой точкой . Поскольку во всем внутреннем пространстве , то первое слагаемое в правой части полученной формулы обращается в нуль, так как . Займемся вторым слагаемым. Будем считать, что радиус малой сферы настолько мал, что функцию внутри этой сферы — постоянная величина. Тогда

Воспользуемся формулой Остроградского, в которой положим , тогда вместо интегрирования по объему будем интегрировать по поверхности малой сферы

Отношение есть элементарный телесный угол , под которым «виден» из точки элемент поверхности сферы. Понятно, что, если точка находится внутри этой сферы, то рассматриваемый интеграл будет равен полному телесному углу, по которым видна поверхность сферы изнутри. Очевидно, что он равен , то есть

Перепишем формулу (3.6) в следующем виде

В случае , для внешней точки получим

Точка P лежит на поверхности. Третий случай — это когда точка не является ни внутренней ни внешней: она лежит на поверхности тела. Можно показать, что в этом случае

noindent поэтому третья формула Грина принимает вид

Формулы (3.7), (3.8) и (3.9) можно записать одной формулой

Гармонической функцией координат называется функция, непрерывная вместе со своими первыми и вторыми производными в некоторой области , удовлетворяющая во всех точках этой области уравнению Лапласа .

Линейная комбинация двух и более гармонических функций есть функция гармоническая.

Пусть U(x,y,z) и V(x,y,z) — две гармонические функции, то есть и . Возьмем их линейную комбинацию . Очевидно, что . Поскольку , , то и , что и доказывает наше утверждение.

Если — гармоническая функция, то все ее частные производные гармонические функции. Доказательство основано на взаимной переставимости оператора Лапласа и производных. Пусть

Линейное преобразование координат (поворот осей, изменение масштаба) не нарушает свойство гармоничности.

Пусть — гармоническая функция. Введем новые координаты

В матричном виде приведенное равенство выглядит следующим образом

Подставим в функцию линейные выражения для , , , для чего воспользуемся вторым из приведенных выше равенств, получим V( . Докажем, что если функция гармоническая, то и является гармонической функцией.

Запишем полученные равенства в матричной форме

Поскольку оператор Лапласа есть квадрат векторного оператора набла , то

В правой части будем иметь

Поскольку матрицы направляющих косинусов являются ортонормированными, их произведения равны единичной матрице и оператор Лапласа принимает вид

Отсюда следует, что оператор Лапласа является инвариантом по отношению к повороту осей, а при изменении масштаба множителем с изменяется на множитель . Другими словами, если , то .

3.2.2 Теоремы о гармонических функциях

Теорема Гаусса: Поток градиента гармонической функции через замкнутую поверхность равен нулю. Потоком называется интеграл по заданной поверхности от нормальной производной функции.

Пусть — гармоническая функция. Предположим, что задана замкнутая поверхность S, ограничивающая область, внутри которой эта функция — гармоническая. Тогда, используя формулу Остроградского (3.1), получим

Но так как функция гармоническая, то , поэтому

В случае, когда — потенциал притяжения, то справедливо уравнение Пуассона , где — плотность притягивающих масс. Тогда формула (3.1) приводит к формуле Гаусса.

Гармоническая функция в замкнутой области D не имеет ни минимума, ни максимума.

Преположим обратное: внутри области существует точка , в которой гармоническая функция имеет максимум. В малой окрестности этой точки на сфере нормальная производная функции будет отрицательной, тогда , что противоречит теореме Гаусса.

textitПотенциал притяжения вне притягивающих масс не может иметь ни минимума, ни максимума; внутри этой области может иметь только максимум.

Любая область вне притягивающего тела есть область определения гармонической функции, внутри которой, согласно теореме 2, не может иметь ни минимума, ни максимума. Предположим обратное: внутри притягивающего тела существует точка , в которой потенциал притяжения достигает минимума. В этой точке справедливо уравнение Пуассона . По формуле Остроградского будем иметь

Mы пришли к противоречию: вследствие минимума внутри малой сферы, нормальная производная на поверхности этой сферы будет положительной, следовательно и приведенные выше интегралы будут положительны, что противоречит сделанному выше выводу. Таким образом, теорему можно считать доказанной.

Теорема Гаусса. Значение гармонической функции в центре сферы равно среднему из значений этой функции на поверхности.

Обратимся к третьей формуле Грина, когда точка внутренняя. Для гармонической функции , поэтому на сфере формула (3.8) принимает вид

На поверхности сферы нормальная производная совпадает с производной по радиус-вектору, поэтому

Кроме того, на поверхности сферы , поэтому

но согласно теореме Гаусса о потоке первое слагаемое в полученном выражении равно нулю, то есть

что и требовалось доказать.

Шаровой функцией степени называется гармоническая функция, являющаяся однородным степенным полиномом вида

где — постоянные. Возьмем сферическую систему координат

где — долгота, — полярное расстояние, — радиус-вектор точки . Очевидно, что

называется сферической функцией .

Итак, шаровая функция степени имеет вид

Существует и другой класс шаровых функций, который приведем здесь без вывода

где — та же сферическая функция, которая входит и в формулу (3.16).

Число постоянных шаровой функции степени равно . Убедимся в этом на при мере шаровой функции третьей степени:

Всего однородный полином третьей степени имеет 10 постоянных. Однако не все постоянные независимы. Шаровые функции подчиняются уравнению Лапласа. Выполнив необходимые выкладки, получим

Следовательно, из 10 постоянных 3 линейно связаны уравнением Лапласа. Остается 10-3=7 независимых постоянных.

Поскольку шаровые функции удовлетворяют уравнению Лапласа, то есть

то должны выполняться и уравнения

В последнем варианте шаровые функции записаны в сферических координатах, поэтому нам необходимо уравнение Лапласа переписать также в сферических координатах.

Из дифференциальной геометрии известно, что если , , — обобщенные координаты, то элемент дуги в этой системе координат будет иметь вид

где , , — коэффициенты Ламе:

Теперь оператор Лапласа можно определить следующим образом (без вывода)

Определим коэффициенты Ламе для сферической системы координат. В данном случае , , , поэтому

Оператор Лапласа для сферических координат будет выглядеть так

Применим этот оператор к шаровой функции вида Очевидно, что оператор Лапласа для шаровой функции равен нулю, поэтому

Таким образом, дифференциальное уравнение для сферической функции порядка имеет вид

Предлагаем самостоятельно убедиться в том, что дифференциальное уравнение для функции входящую в шаровую функцию второго рода совпадает с уравнением (3.20).

Заменим переменную на . тогда . Очевидно, что

поэтому дифференциальное уравнение (3.20) можно переписать так

Будем искать решение этого уравнения в виде . Подставив это выражение в дифференциальное уравнение, будем иметь

Умножив каждый член полученного выражения на и поделив на , получим

Видим, что первые два члена зависят только от , а последний — только от Для того, чтобы уравнение выполнялось для любых и , необходимо, чтобы эти функции выродились в константы. Например, уравнение будет выполняться, если

Второе уравнение есть уравнение гармонических колебаний

Его решение для любых действительных значений имеет вид

где и — постоянные интегрирования. Решение первого из приведенных выше уравнений, зависит как от постоянной , так и от постоянной . Обозначив решение через , получим

Функция при целочисленных значениях носит название присоединенной (ассоциативной) функции Лежандра. В случае , эти функции становятся степенными полиномами, которые называются полиномами Лежандра. Полагая в уравнении (3.23) , получим дифференциальное уравнение для полиномов Лежандра

В теории специальных функций свойства функций и полиномов Лежандра достаточно хорошо изучены. Приведем лишь некоторые сведения (без вывода), которые могут пригодиться в нашем курсе. Присоединенные функции Лежандра и полиномы Лежандра связаны между собой соотношением

Подводя итог сказанному, выпишем окончательный вид решения дифференциального уравнения для сферических функций

Заметим, что порядок производной в (3.25) не может быть больше степени полинома Лежандра. По этой причине постоянные и называют степенью и порядком сферических функций.